6.11: Longitud del arco
- Page ID
- 107271
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Porción de la circunferencia de un círculo.
Una forma de medir los arcos es en grados. Esto se llama la “medida de arco” o “medida de grado” (ver Arcos en Círculos). Los arcos también se pueden medir en longitud, como una porción de la circunferencia. La longitud del arco es la longitud de un arco o una porción de la circunferencia de un círculo. La longitud del arco está directamente relacionada con la medida del arco de grado.
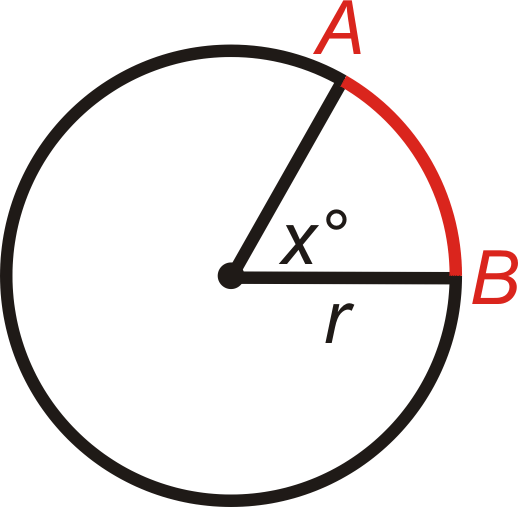
Fórmula de longitud de arco: La longitud de\(\widehat{AB}=\dfrac{m\widehat{AB}}{360^{\circ}}\cdot \pi d\) o\(\dfrac{m\widehat{AB}}{360^{\circ}}\cdot 2\pi r\).
¿Y si te dieran la medida del ángulo del arco de un círculo? ¿Cómo pudiste encontrar la longitud de ese arco?
Ejemplo\(\PageIndex{1}\)
Encuentra la longitud del arco de\(\widehat{PQ}\) pulg\(\bigodot A\). Deja tus respuestas en términos de\(\pi\).
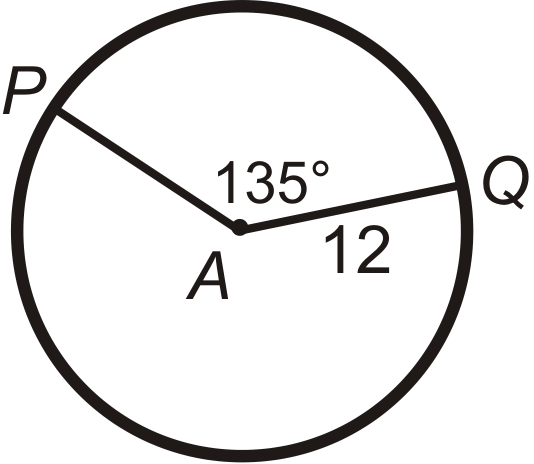
Solución
Usa la fórmula Longitud del Arco.
\(\begin{aligned} \widehat{PQ}&=\dfrac{135}{360}\cdot 2\pi (12) \\ \widehat{PQ}&=\dfrac{3}{8}\cdot 24\pi \\ \widehat{PQ}&=9\pi \end{aligned}\)
Ejemplo\(\PageIndex{2}\)
Una pizza grande típica tiene un diámetro de 14 pulgadas y se corta en 8 piezas. Piensa en la corteza como la circunferencia de la pizza. Encuentra la longitud de la corteza para toda la pizza. Después, encuentra la longitud de la corteza para una pieza de pizza si toda la pizza se corta en 8 trozos.
Solución
Toda la longitud de la corteza, o la circunferencia de la pizza, es\(14\pi \approx 44 in.\) In\(\dfrac{1}{8}\) de la pizza, una pieza tendría\(\dfrac{44}{8}\approx 5.5 inches\) de corteza.
Ejemplo\(\PageIndex{3}\)
Encuentra la longitud de\(\widehat{PQ}\). Deja tu respuesta en términos de\(\pi\).
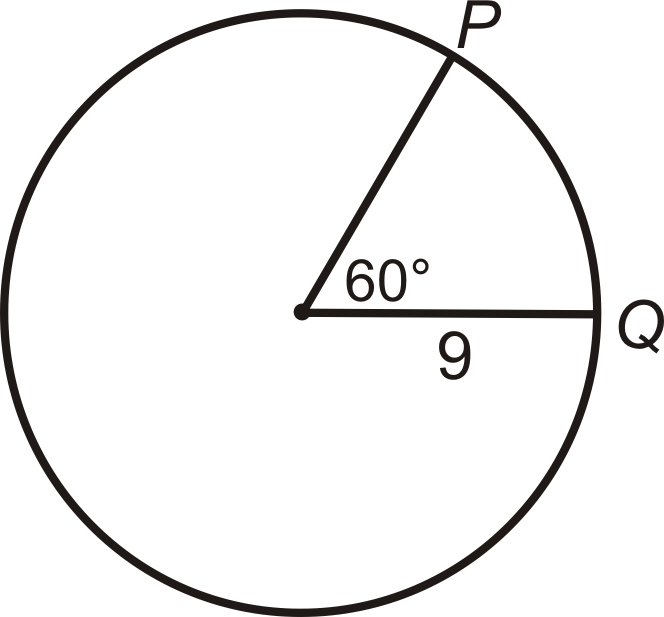
Solución
En la imagen, el ángulo central que corresponde con\(\widehat{PQ}\) es\(60^{\circ}\). Esto significa que\(m\widehat{PQ}=60^{\circ}\). Piense en la longitud del arco como una porción de la circunferencia. Hay\(360^{\circ}\) en un círculo, entonces 60^ {\ circ}\) serían 16 de ese (\(60^{\circ}360^{\circ}=16\)). Por lo tanto, la longitud de\(\widehat{PQ}\) es 16 de la circunferencia. \ texto {longitud de}\ anchohat {PQ} =16\ cdot 2\ pi (9) =3\ pi\ texto {unidades}\).
Ejemplo\(\PageIndex{4}\)
La longitud del arco de un círculo es\(\widehat{AB}=6\pi\) y es 14 la circunferencia. Encuentra el radio del círculo.
Solución
Si 6\ pi es 14 la circunferencia, entonces la circunferencia total es\(4(6\pi )=24\pi\). Para encontrar el radio, conecte esto a la fórmula de circunferencia y resuelva para r.
\(\begin{aligned} 24\pi =2\pi r \\ 12 \text{ units }=r \end{aligned}\)
Ejemplo\(\PageIndex{5}\)
Encuentra la medida del ángulo central o\(\widehat{PQ}\).
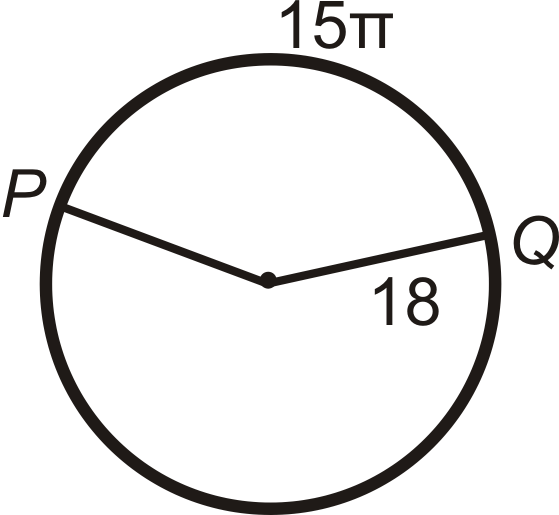
Solución
Vamos a enchufar lo que sabemos a la Fórmula de Longitud de Arco.
\(\begin{aligned}15\pi &=m\widehat{PQ}360^{\circ}\cdot 2\pi (18) \\ 15&=m\widehat{PQ}10^{\circ} \\ 150^{\circ}&=m\widehat{PQ}\end{aligned}\)
Revisar
Encuentra la longitud del arco de\(\widehat{PQ}\) pulg\(\bigodot A\). Deja tus respuestas en términos de\(\pi\).
-
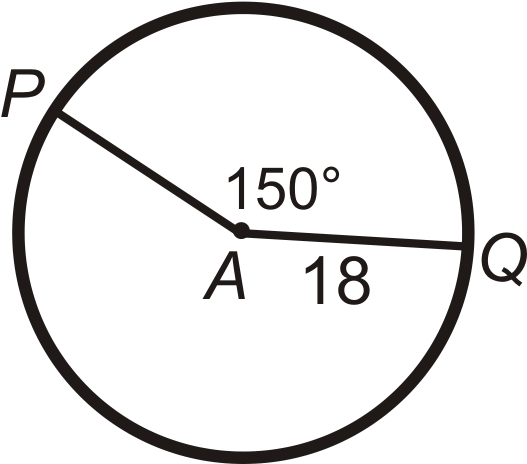
Figura\(\PageIndex{6}\) -
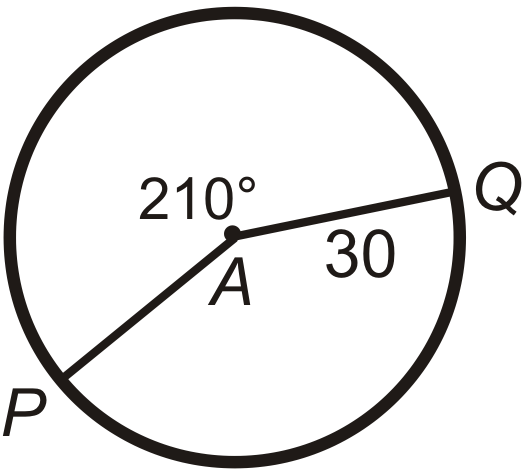
Figura\(\PageIndex{7}\) -
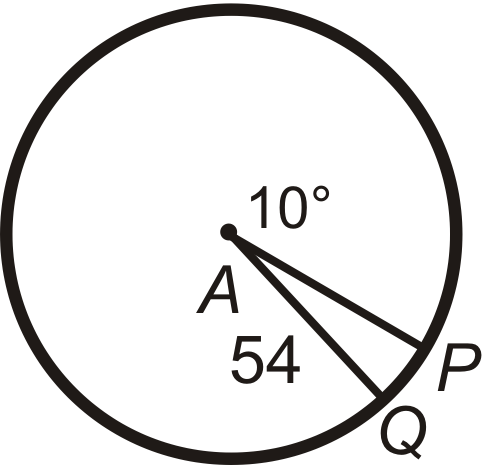
Figura\(\PageIndex{8}\) -
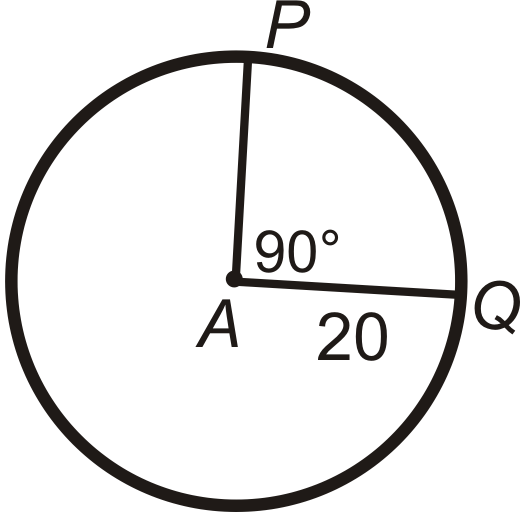
Figura\(\PageIndex{9}\)
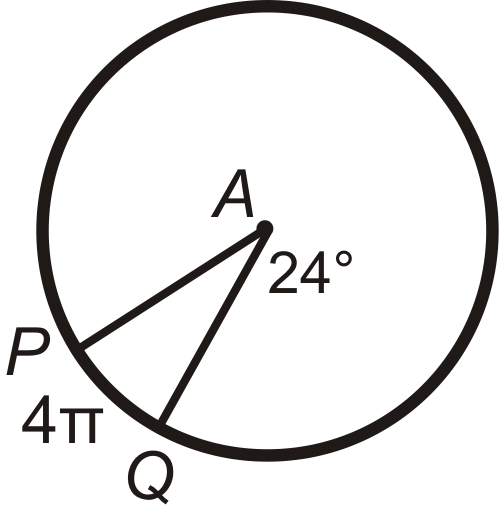
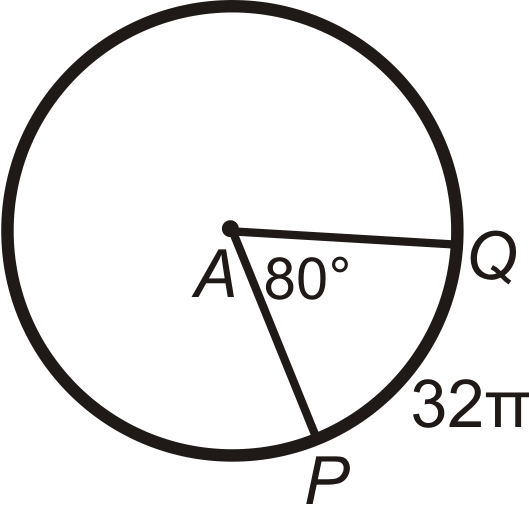
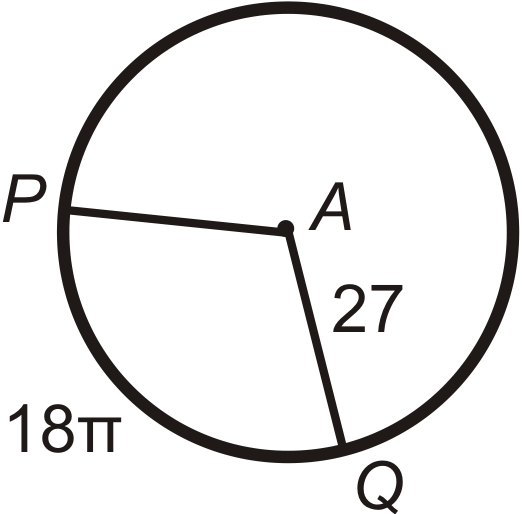
Encuentra\(PA\) (el radio) en\(\bigodot A\). Deja tu respuesta en términos de\(\pi \).
-
Figura\(\PageIndex{11}\) -
Figura\(\PageIndex{12}\) -
Figura\(\PageIndex{13}\)
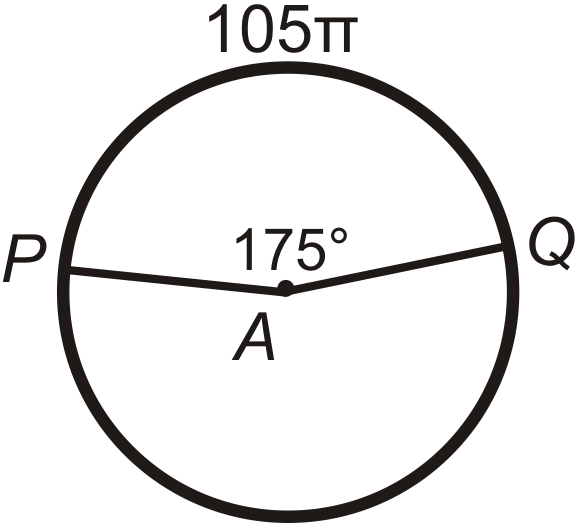
Encuentra el ángulo central o\(m\widehat{PQ}\) en\(\bigodot A\). Redondear cualquier respuesta decimal a la décima más cercana.
-
Figura\(\PageIndex{14}\) -
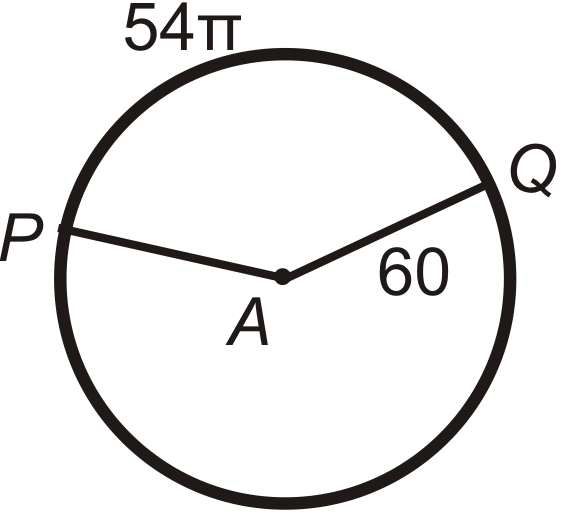
Figura\(\PageIndex{15}\) -
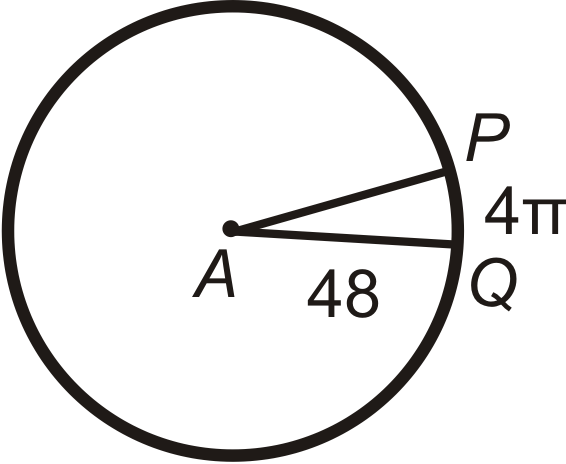
Figura\(\PageIndex{16}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.9.
vocabulario
| Término | Definición |
|---|---|
| acorde | Un segmento de línea cuyos extremos están en un círculo. |
| círculo | El conjunto de todos los puntos que están a la misma distancia de un punto específico, llamado el centro. |
| diámetro | Un acorde que pasa por el centro del círculo. La longitud de un diámetro es dos veces la longitud de un radio. |
| pi | (o\(\pi\)) La relación entre la circunferencia de un círculo y su diámetro. |
| radio | La distancia desde el centro hasta el borde exterior de un círculo. |
| Arc | Un arco es una sección de la circunferencia de un círculo. |
| longitud del arco | En cálculo, la longitud del arco es la longitud de una curva de función plana sobre un intervalo. |
| Circunferencia | La circunferencia de un círculo es la medida de la distancia alrededor del borde exterior de un círculo. |
| Dilatación | Reducir o agrandar una figura según un factor de escala es una dilatación. |
| radián | Un radián es una unidad de ángulo que es igual al ángulo creado en el centro de un círculo cuyo arco es igual en longitud al radio. |
| Sector | Un sector de un círculo es una porción de un círculo contenida entre dos radios del círculo. Los sectores se pueden medir en grados. |
Recursos adicionales
Elemento Interactivo
Video: Principios de longitud de arco - Básico
Actividades: Preguntas de discusión sobre la longitud del arco
Ayudas de estudio: Guía de estudio de circunferencia y longitud de arco
Práctica: Longitud del arco
Mundo real: ¿Qué tan lejos está Londres?