6.13: Segmentos a partir de Acordes
- Page ID
- 107239
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Aplicar el Teorema de Acordes de Intersección.
Cuando tenemos dos acordes que se cruzan dentro de un círculo, como se muestra a continuación, los dos triángulos que resultan son similares.
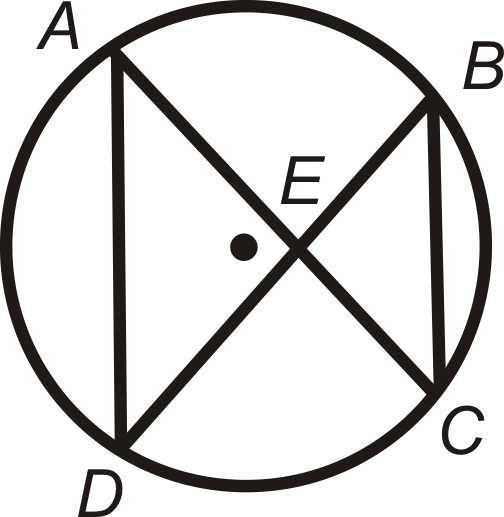
Esto hace que los lados correspondientes en cada triángulo sean proporcionales y conduce a una relación entre los segmentos de los acordes, como se establece en el Teorema de Acordes de Intersección.
Teorema de acordes de intersección: Si dos acordes se cruzan dentro de un círculo de manera que uno se divide en segmentos de longitud a y b y el otro en segmentos de longitud\(c\) y\(d\) luego\(ab=cd\).
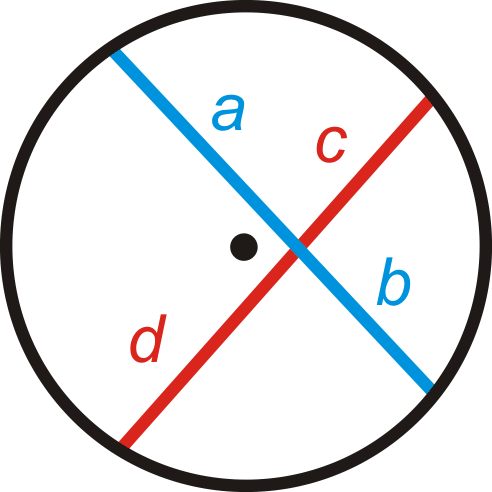
¿Y si te dieran un círculo con dos acordes que se cruzan entre sí? ¿Cómo podría usar la longitud de algunos de los segmentos formados por su intersección para determinar las longitudes de los segmentos desconocidos?
Ejemplo\(\PageIndex{1}\)
Encuentra\(x\). Simplifica cualquier tipo de radicales.
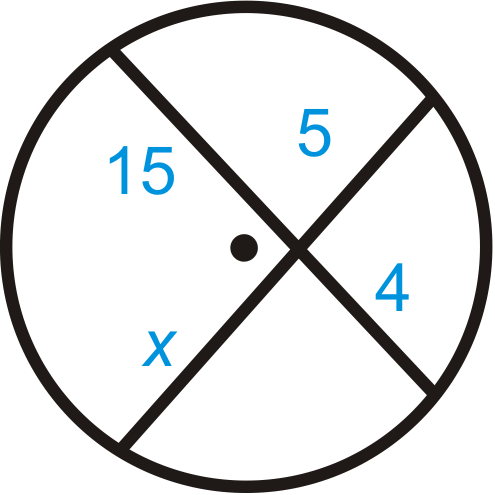
Solución
Usa el Teorema de Acordes de Intersección.
\(15\cdot 4=5\cdot x\)
\(60=5x\)
\(x=12\)
Ejemplo\(\PageIndex{2}\)
Encuentra\(x\). Simplifica cualquier tipo de radicales.
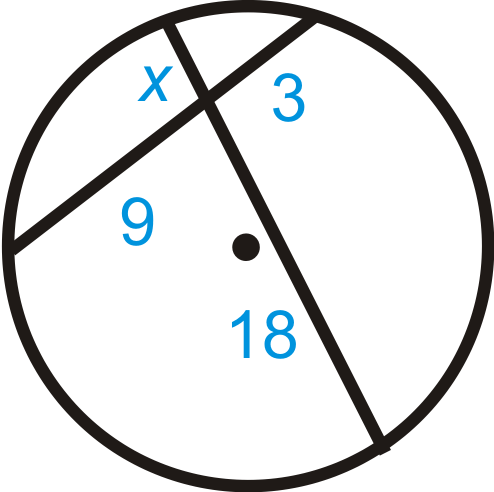
Solución
Usa el Teorema de Acordes de Intersección.
\(\begin{aligned} 18\cdot x&=9\cdot 3 \\ 18x&=27 \\ x&=1.5\end{aligned}\)
Ejemplo\(\PageIndex{3}\)
Encuentra x en cada diagrama a continuación.
-
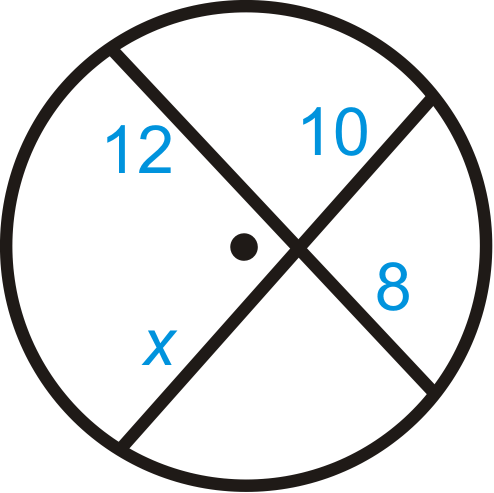
Figura\(\PageIndex{5}\) -
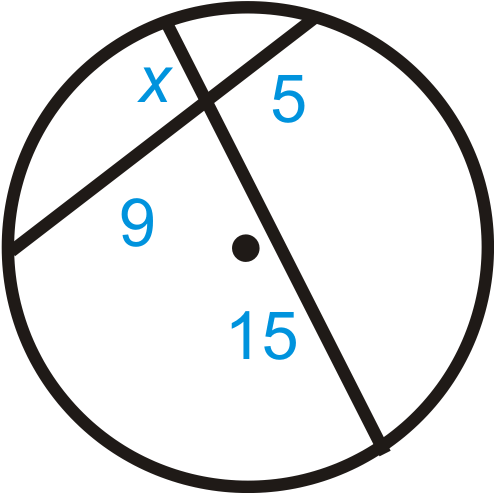
Figura\ (\ pageIndex {6}\
Solución
- Usa la fórmula del Teorema de Acordes de Intersección.
\(\begin{aligned}12\cdot 8 &=10\cdot x \\ 96&=10x \\ 9.6&=x\end{aligned}\)
- Usa la fórmula del Teorema de Acordes de Intersección.
\(\begin{aligned} x\cdot 15&=5\cdot 9 \\ 15x&=45 \\ x&=3 \end{aligned}\)
Ejemplo\(\PageIndex{4}\)
Resuelva para\(x\) en cada diagrama a continuación.
-
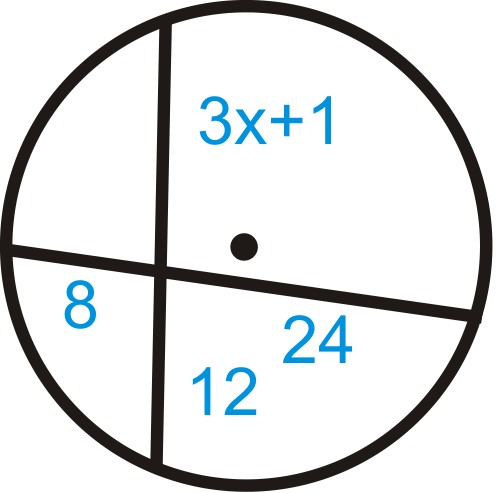
Figura\(\PageIndex{7}\) -
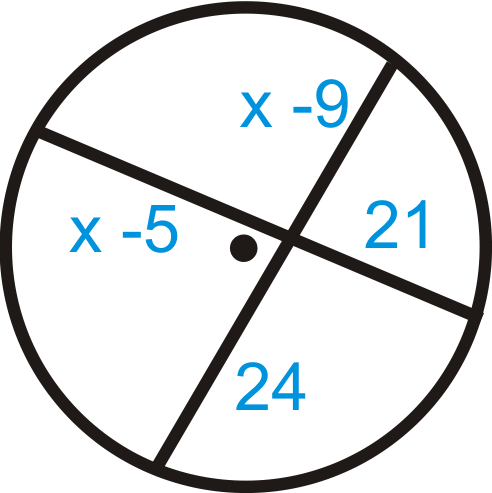
Figura\(\PageIndex{8}\)
Solución
- Usa el Teorema de Acordes de Intersección.
\(\begin{aligned} 8\cdot 24&=(3x+1)\cdot 12 \\192&=36x+12 \\ 180&=36x \\ 5&=x\end{aligned}\)
- Usa el Teorema de Acordes de Intersección.
\(\begin{aligned} (x−5)21&=(x−9)24 \\ 21x−105&=24x \\ 111&=3x \\ 37−216&=x \end{aligned}\)
Ejemplo\(\PageIndex{5}\)
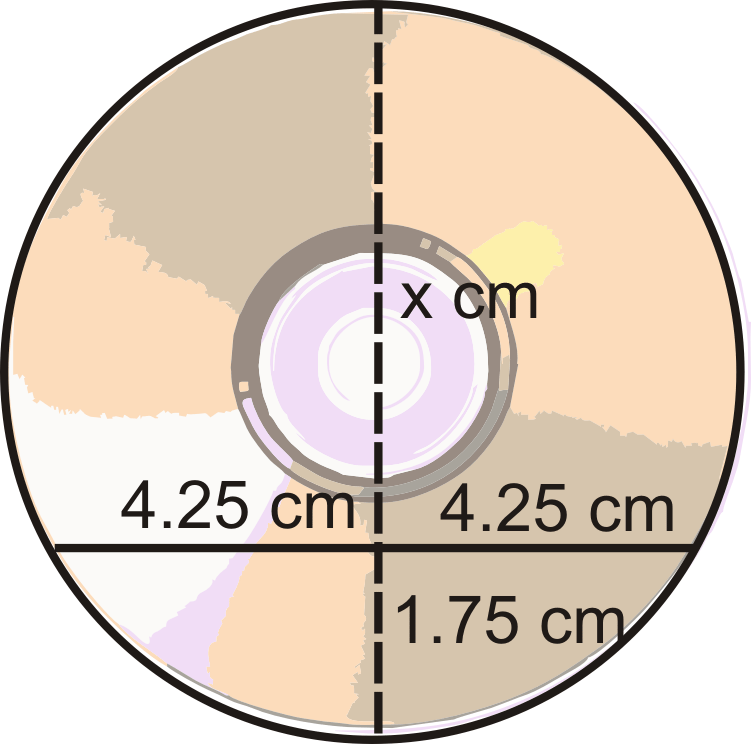
Ismael encontró una pieza rota de un CD en su auto. Coloca una regla en dos puntos del borde, y la longitud del acorde es de 9.5 cm. La distancia desde el punto medio de esta cuerda hasta el punto más cercano en el borde es de 1.75 cm. Encuentra el diámetro del CD.
Solución
Piense en esto como dos acordes que se cruzan entre sí. Si tuviéramos que extender el segmento de 1.75 cm, sería un diámetro. Entonces, si encontramos x en el diagrama de abajo y lo agregamos a 1.75 cm, encontraríamos el diámetro.
\(\begin{aligned} 4.25\cdot 4.25&=1.75\cdot x \\ 18.0625&=1.75x\end{aligned}\)
\(x\approx 10.3 cm, making the diameter 10.3+1.75\approx 12 cm, which\: is\: the actual diameter of a CD.\)
Revisar
Rellene los espacios en blanco para cada problema a continuación y luego resuelva el segmento faltante.
-
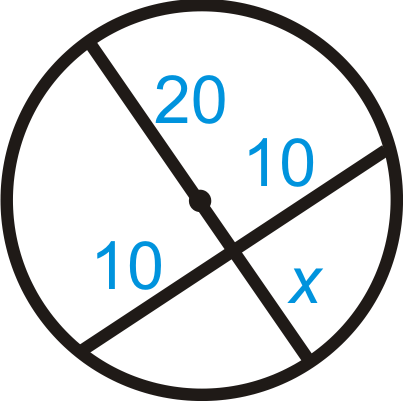
Figura\(\PageIndex{11}\)
\(20x=_______\)
-
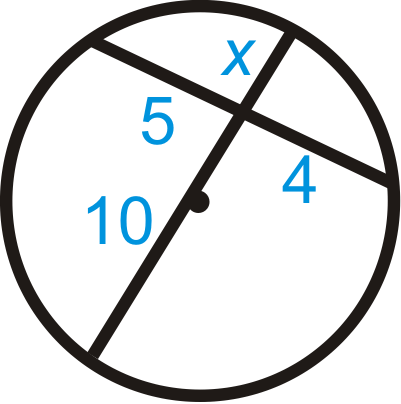
Figura\(\PageIndex{12}\)
\(\text{_______}\cdot 4=\text{_______}\cdot x\)
Encuentra x en cada diagrama a continuación. Simplifica cualquier tipo de radicales.
-
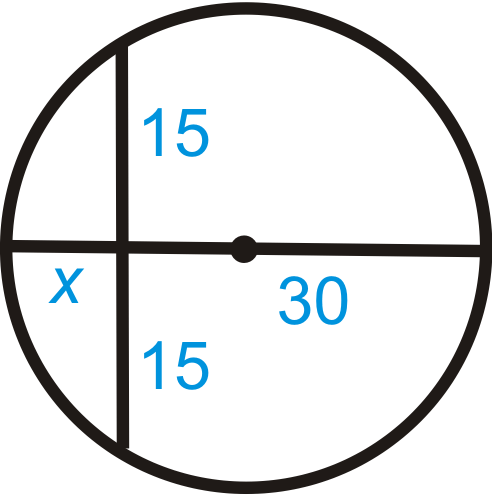
Figura\(\PageIndex{13}\) -
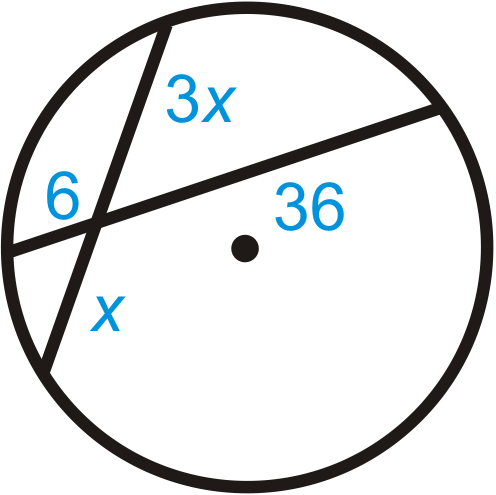
Figura\(\PageIndex{14}\) -
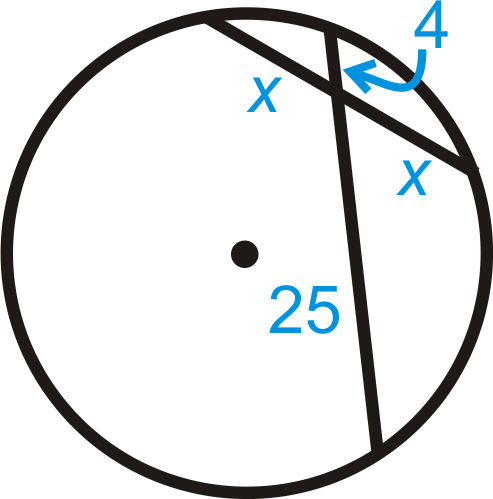
Figura\(\PageIndex{15}\)
Encuentra el valor de\(x\).
-
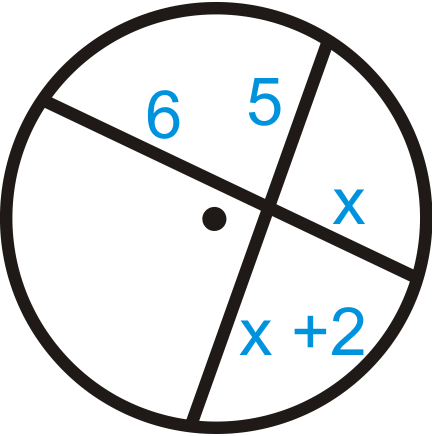Figura\(\PageIndex{16}\) -
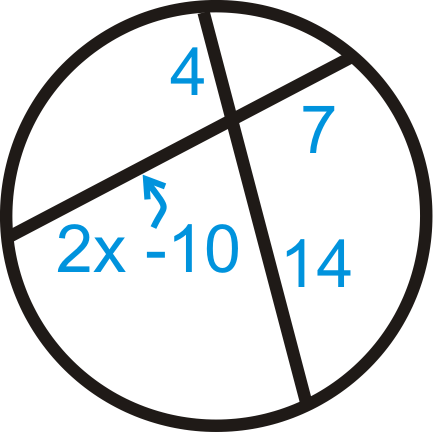
Figura\(\PageIndex{17}\) -
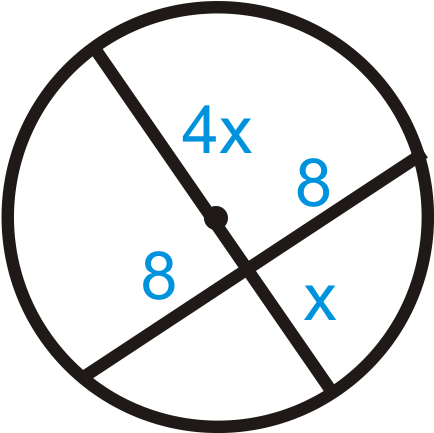
Figura\(\PageIndex{18}\) - Suzie encontró un trozo de una placa rota. Ella coloca una regla a través de dos puntos en el borde, y la longitud del acorde es de 6 pulgadas. La distancia desde el punto medio de esta cuerda hasta el punto más cercano en la llanta es de 1 pulgada. Encuentra el diámetro de la placa.
- Rellene los espacios en blanco de la prueba del Teorema de Acordes Intersecantes.
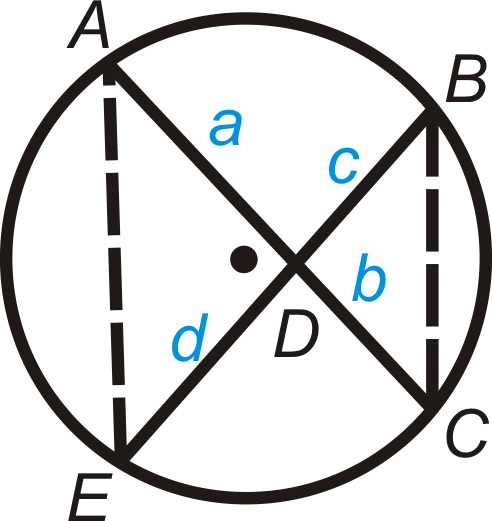
Figura\(\PageIndex{19}\)
Dado: Acordes de intersección\(\overline{AC}\) y\(\overline{BE}\).
Demostrar:\(ab=cd\)
| Comunicado | Razón |
|---|---|
| 1. Acordes de intersección\(\overline{AC}\) y\(\overline{BE}\) con segmentos\(a\),\(b\),\(c\), y\(d\). | 1. |
| 2. | 2. Teorema de Ángulos Congruentes con Inscripciones |
| 3. \(\Delta ADE\sim \Delta BDC\) | 3. |
| 4. | 4. Las partes correspondientes de triángulos similares son proporcionales |
| 5. \(ab=cd\) | 5. |
vocabulario
| Término | Definición |
|---|---|
| ángulo central | Un ángulo formado por dos radios y cuyo vértice se encuentra en el centro del círculo. |
| acorde | Un segmento de línea cuyos extremos están en un círculo. |
| círculo | El conjunto de todos los puntos que están a la misma distancia de un punto específico, llamado el centro. |
| diámetro | Un acorde que pasa por el centro del círculo. La longitud de un diámetro es dos veces la longitud de un radio. |
| ángulo inscrito | Un ángulo con su vértice en el círculo y cuyos lados son acordes. |
| arco interceptado | El arco que se encuentra dentro de un ángulo inscrito y cuyos extremos están en el ángulo. |
| radio | La distancia desde el centro hasta el borde exterior de un círculo. |
| Teorema de Acordes Intersecantes | De acuerdo con el Teorema de Acordes de Intersección, si dos acordes se cruzan dentro de un círculo de manera que uno se divide en segmentos de longitud\(a\)\(b\) y el otro en segmentos de longitud\(c\) y\(d\), entonces\(ab = cd\). |
Recursos adicionales
Elemento Interactivo
Video: Segmentos a partir de los Principios de Acordes - Básico
Actividades: Segmentos a partir de acordes Preguntas de discusión
Ayudas de estudio: Círculos: Segmentos y longitudes Guía de estudio
Práctica: Segmentos a partir de acordes