6.14: Ángulos Inscritos en Círculos
- Page ID
- 107283
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Vértice en un círculo y acordes como lados, y cuya medida equivale a la mitad del arco interceptado.
Un ángulo inscrito es un ángulo con su vértice en el círculo y cuyos lados son acordes. El arco interceptado es el arco que se encuentra dentro del ángulo inscrito y cuyos extremos están en el ángulo. El vértice de un ángulo inscrito puede estar en cualquier parte del círculo siempre y cuando sus lados se crucen con el círculo para formar un arco interceptado.
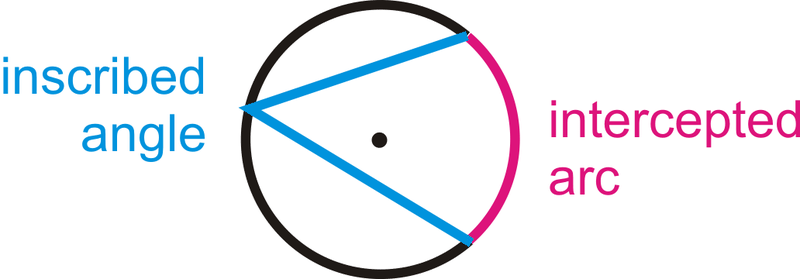
El Teorema del Ángulo Inscrito establece que la medida de un ángulo inscrito es la mitad de la medida de su arco interceptado.
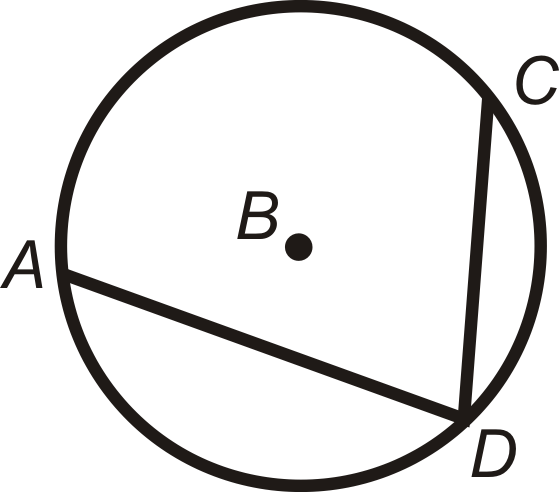
\(m\angle ADC=\dfrac{1}{2}m\widehat{AC}\)y\(m\widehat{AC}=2m\angle ADC\)
Los ángulos inscritos que interceptan el mismo arco son congruentes. Esto se llama Teorema de Ángulos Inscritos Congruentes y se muestra a continuación.
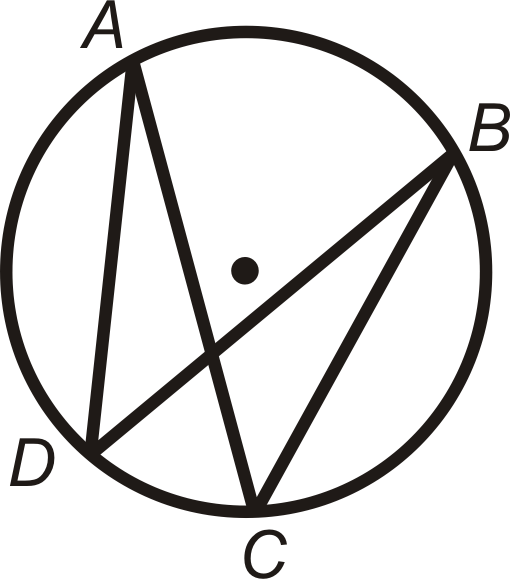
\(\angle ADB\)e\(\angle ACB\) interceptar\(\widehat{AB}\), entonces\(m\angle ADB=m\angle ACB\). De igual manera,\(\angle DAC\) e\(\angle DBC\) interceptar\(\widehat{DC}\), entonces\(m\angle DAC=m\angle DBC\).
Un ángulo intercepta un semicírculo si y solo si es un ángulo recto (Teorema de semicírculo). Cada vez que se inscribe un ángulo recto en un círculo, los extremos del ángulo son los extremos de un diámetro y el diámetro es la hipotenusa.
¿Y si tuvieras un círculo con dos acordes que comparten un punto final común? ¿Cómo podrías usar el arco formado por esos acordes para determinar la medida del ángulo que hacen esos acordes dentro del círculo?
Ejemplo\(\PageIndex{1}\)
Encontrar\(m\widehat{DC}\) y\(m\angle ADB\).
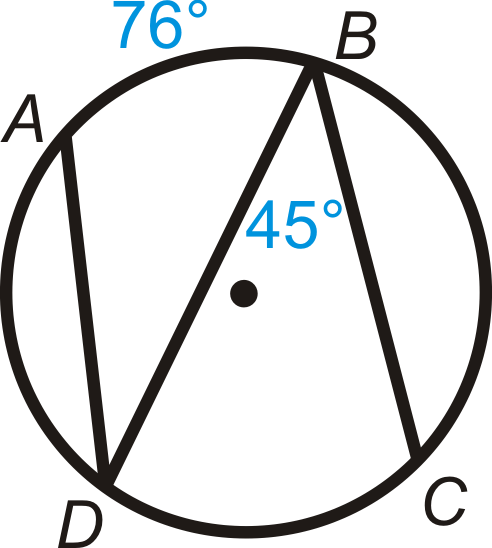
Solución
Del Teorema del Ángulo Inscrito:
\(\begin{aligned} m\widehat{DC}&=2\cdot 45^{\circ}=90^{\circ} \\ m\angle ADB&=12\cdot 76^{\circ}=38^{\circ}\end{aligned}\)
Ejemplo\(\PageIndex{2}\)
Encontrar\(m\angle ADB\) y\(m\angle ACB\).
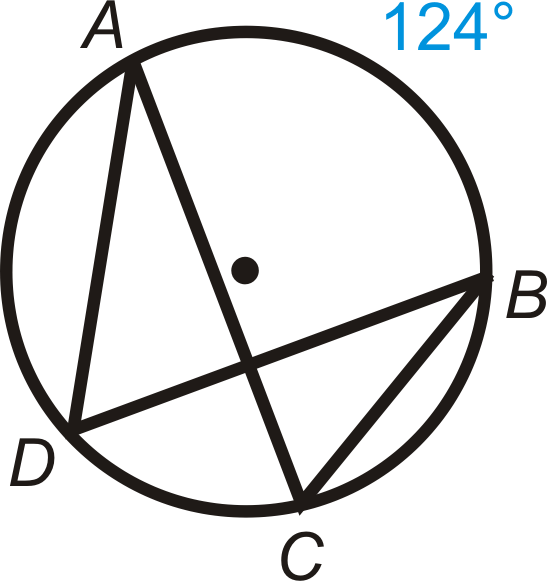
Solución
El arco interceptado para ambos ángulos es\(\widehat{AB}\). Por lo tanto,
\(\begin{aligned} m\angle ADB&=12\cdot 124^{\circ}=62^{\circ} \\ m\angle ACB&=12\cdot 124^{\circ}=62^{\circ}\end{aligned}\)
Ejemplo\(\PageIndex{3}\)
Encuentra\(m\angle DAB\) en\(\bigodot C\).
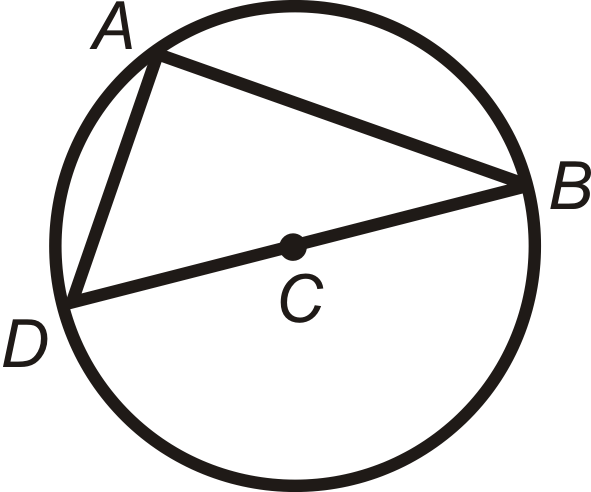
Solución
C es el centro, así\(\overline{DB}\) es un diámetro. \(\angle DAB\)los puntos finales están en el diámetro, por lo que el ángulo central es\(180^{\circ}\).
\(m\angle DAB=\dfrac{1}{2}\cdot 180^{\circ}=90^{\circ}\).
Ejemplo\(\PageIndex{4}\)
Rellene el espacio en blanco: Un ángulo inscrito es ____________ la medida del arco interceptado.
Solución
la mitad
Ejemplo\(\PageIndex{5}\)
Rellene el espacio en blanco: Un ángulo central es ________________ la medida del arco interceptado.
Solución
igual a
Revisar
Rellene los espacios en blanco.
- Un ángulo inscrito en un ________________ es\(90^{\circ}\).
- Dos ángulos inscritos que interceptan el mismo arco son _______________.
- Los lados de un ángulo inscrito son ___________________.
- Dibujar ángulo inscrito\(\angle JKL\) en\(\bigodot M\). Después dibuja ángulo central\(\angle JML\). ¿Cómo se relacionan los dos ángulos?
Encuentra el valor de\(x\) y/o\(y\) en\(\bigodot A\).
-
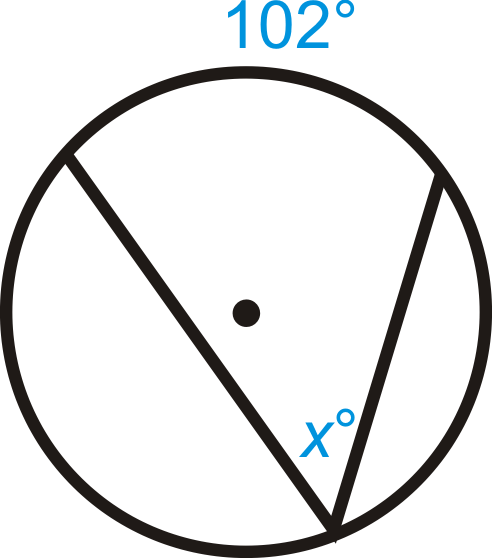 Figura\(\PageIndex{7}\)
Figura\(\PageIndex{7}\) -
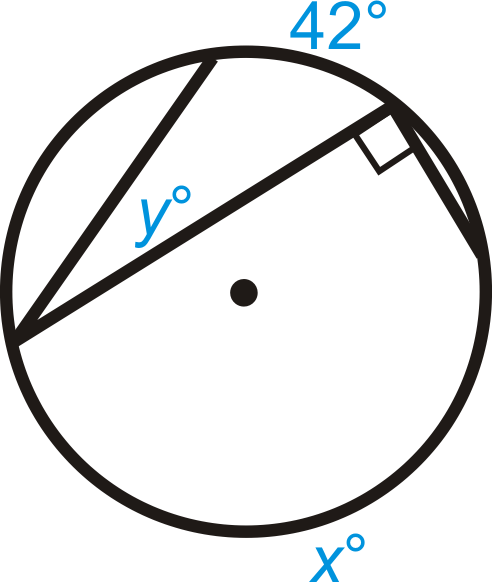 Figura\(\PageIndex{8}\)
Figura\(\PageIndex{8}\) -
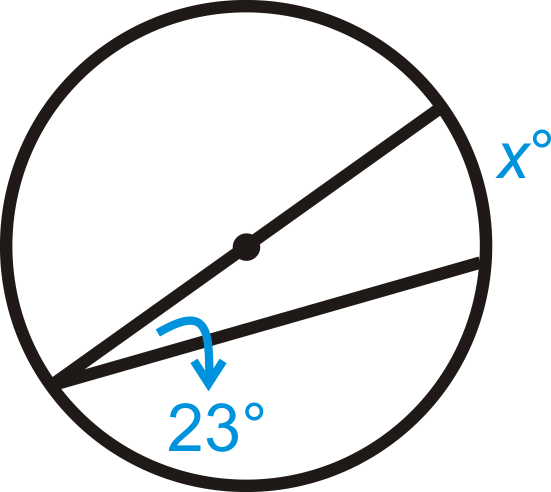 Figura\(\PageIndex{9}\)
Figura\(\PageIndex{9}\) -
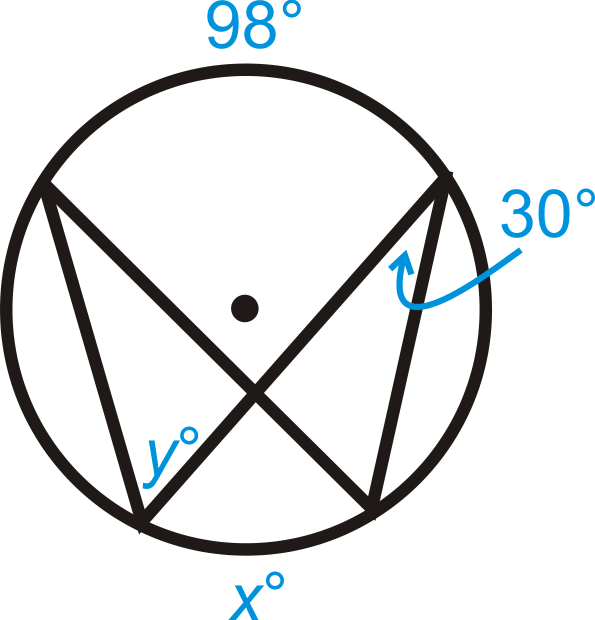 Figura\(\PageIndex{10}\)
Figura\(\PageIndex{10}\) -
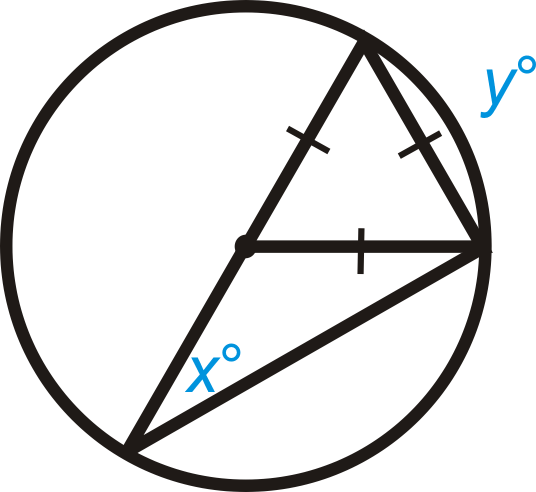 Figura\(\PageIndex{11}\)
Figura\(\PageIndex{11}\)
Resolver para\(x\).
-
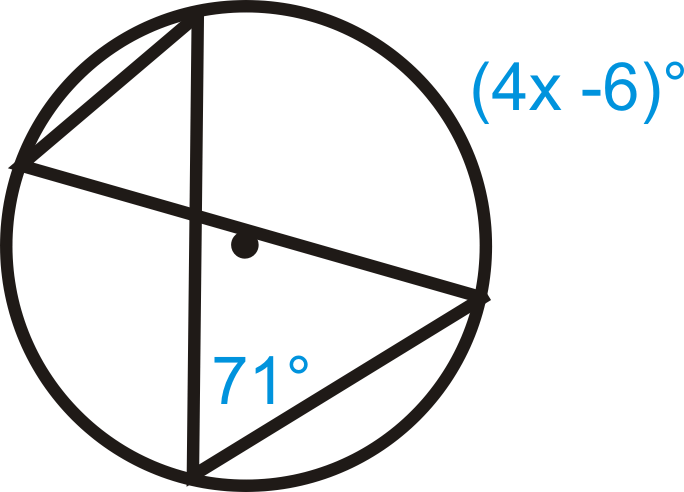 Figura\(\PageIndex{12}\)
Figura\(\PageIndex{12}\) -
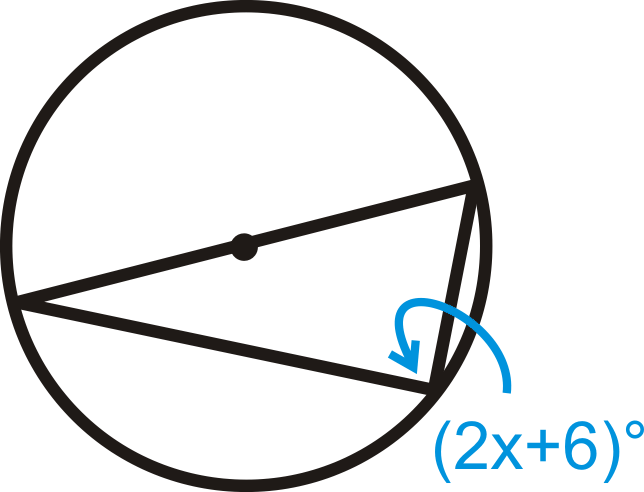 Figura\(\PageIndex{13}\)
Figura\(\PageIndex{13}\) -
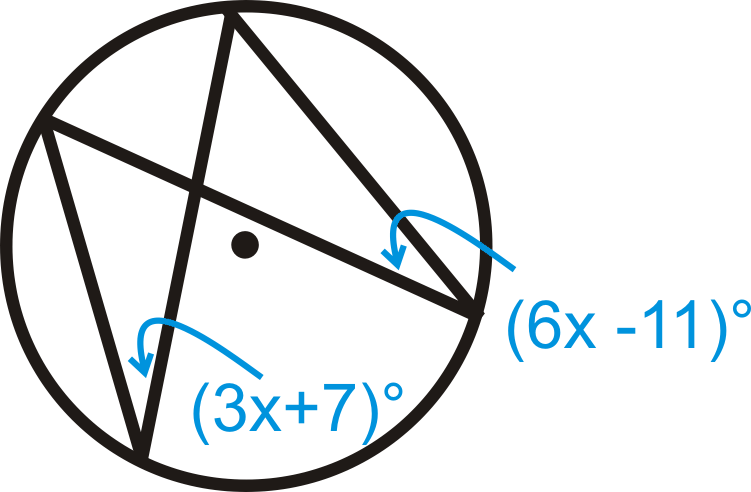 Figura\(\PageIndex{14}\)
Figura\(\PageIndex{14}\) -
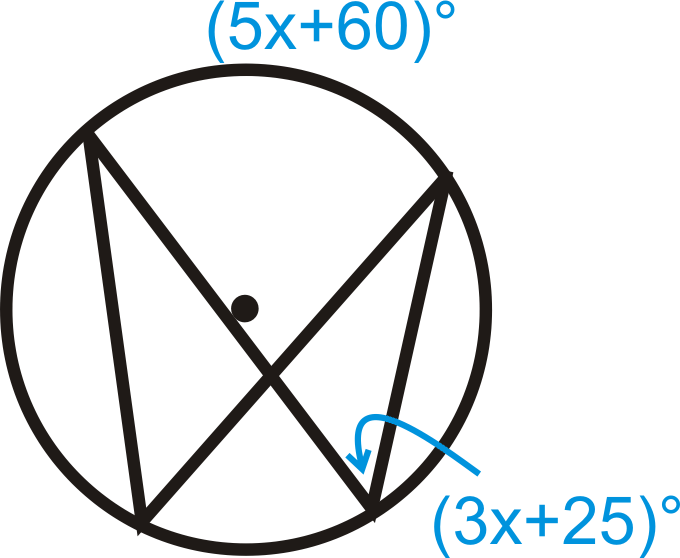 Figura\(\PageIndex{15}\)
Figura\(\PageIndex{15}\) - Rellene los espacios en blanco de la prueba del Teorema del Ángulo Inscrito.
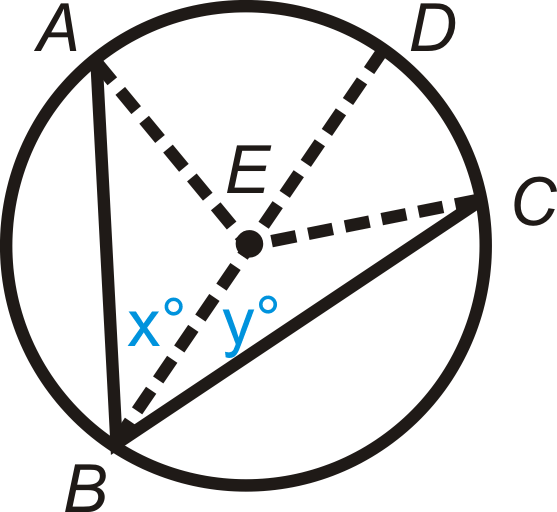 Figura\(\PageIndex{16}\)
Figura\(\PageIndex{16}\)
Dado: Inscrito\(\angle ABC\) y diámetro\(\overline{BD}\)
Demostrar:\ (m\ ángulo ABC=12m\ anchohat {AC}
| Declaración | Razón |
|---|---|
|
1. Inscrito\(\angle ABC\) y diámetro\(\overline{BD}\) \(m\angle ABE=x^{\circ}\)y\(m\angle CBE=y^{\circ}\) |
1. |
| 2. \(x^{\circ}+y^{\circ}=m\angle ABC\) | 2. |
| 3. | 3. Todos los radios son congruentes |
| 4. | 4. Definición de un triángulo isósceles |
| 5. \(m\angle EAB=x^{\circ}\)y\(m\angle ECB=y^{\circ}\) | 5. |
| 6. \(m\angle AED=2x^{\circ}\)y\(m\angle CED=2y^{\circ}\) | 6. |
| 7. \(m\widehat{AD}=2x^{\circ}\)y\(m\widehat{DC}=2y^{\circ}\) | 7. |
| 8. | 8. Postulado de adición de arco |
| 9. \(m\widehat{AC}=2x^{\circ}+2y^{\circ}\) | 9. |
| 10. | 10. PoE distributivo |
| 11. \(m\widehat{AC}=2m\angle ABC\) | 11. |
| 12. \(m\angle ABC=\dfrac{1}{2}m\widehat{AC}\) | 12. |
vocabulario
| Término | Definición |
|---|---|
| ángulo central | Un ángulo formado por dos radios y cuyo vértice se encuentra en el centro del círculo. |
| acorde | Un segmento de línea cuyos extremos están en un círculo. |
| círculo | El conjunto de todos los puntos que están a la misma distancia de un punto específico, llamado el centro. |
| diámetro | Un acorde que pasa por el centro del círculo. La longitud de un diámetro es dos veces la longitud de un radio. |
| Ángulo con Inscritos | Un ángulo inscrito es un ángulo con su vértice en el círculo. La medida de un ángulo inscrito es la mitad de la medida de su arco interceptado. |
| arco interceptado | El arco que se encuentra dentro de un ángulo inscrito y cuyos extremos están en el ángulo. |
| radio | La distancia desde el centro hasta el borde exterior de un círculo. |
| Arc | Un arco es una sección de la circunferencia de un círculo. |
| Intercepta | Las intercepciones de una curva son las ubicaciones donde la curva interseca los ejes x e y. Una intersección x es un punto en el que la curva se cruza con el eje x. Una intersección y es un punto en el que la curva cruza el eje y. |
| Teorema del Ángulo con Inscritos | El Teorema del Ángulo Inscrito establece que la medida de un ángulo inscrito es la mitad de la medida de su arco interceptado. |
| Teorema semicírculo | El Teorema de Semicírculo establece que cada vez que se inscribe un ángulo recto en un círculo, los extremos del ángulo son los extremos de un diámetro y el diámetro es la hipotenusa. |
Recursos adicionales
Elemento interactivo
Video: Ángulos Inscritos en Círculos Principios - Básico
Actividades: Ángulos inscritos en círculos Preguntas de discusión
Ayudas de estudio: Guía de estudio Inscritos en Círculos
Práctica: Ángulos inscritos en círculos

