Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

Inicio
Educación Básica
Geometría
7: Similitud
7.2: Relación y Proporción en Cifras Similares

7.2: Relación y Proporción en Cifras Similares

Última actualización

30 oct 2022
Guardar como PDF
- 7.1: Cifras similares
- 7.3: Polígonos y Factores de Escala Similares

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Simplifique las formas de comparar dos números.

Proporciones

Una proporción son dos proporciones que se establecen iguales entre sí. Por lo general, las proporciones en proporciones se escriben en forma de fracción. Un ejemplo de una proporción es $\dfrac{2}{x}=510$ . Para resolver una proporción, es necesario multiplicar de manera cruzada. El Teorema de Multiplicación Cruzada, que nos permite resolver proporciones utilizando este método, establece que si $a$ $b$ , $c$ ,, y $d$ son números reales, con $b\neq 0$ y $d\neq 0$ y si $\dfrac{a}{b}=\dfrac{c}{d}$ , entonces $\dfrac{a}{d}=\dfrac{b}{c}$ . La multiplicación cruzada nos permite deshacernos de las fracciones de nuestra ecuación. El Teorema de Multiplicación Cruzada tiene varios subteoremas, llamados corolarios.

Corolario #1: Si $a$ , $b$ , $c$ , y $d$ son distintos de cero y $\dfrac{a}{b}=\dfrac{c}{d}$ , entonces $\dfrac{a}{c}=\dfrac{b}{d}$ .

Interruptor $b$ y $c$ .

Corolario #2: Si $a$ , $b$ , $c$ , y $d$ son distintos de cero y $\dfrac{a}{b}=\dfrac{c}{d}$ , entonces $\dfrac{d}{b}=\dfrac{c}{a}$ .

Interruptor $a$ y $d$ .

Corolario #3: Si $a$ , $b$ , $c$ , y $d$ son distintos de cero y $\dfrac{a}{b}=\dfrac{c}{d}$ \), entonces $\dfrac{b}{a}=\dfrac{c}{d}$ .

Voltear cada proporción boca abajo.

Corolario #4: Si $a$ , $b$ , $c$ , y $d$ son diferentes de cero y\ dfrac {a} {b} =\ dfrac {c} {d}\), entonces $\dfrac{a+b}{b}=\dfrac{c+d}{d}$ .

Corolario #5: Si $a$ , $b$ , $c$ , y $d$ son distintos de cero y $\dfrac{a}{b}=\dfrac{c}{d}$ , entonces $\dfrac{a−b}{b}=\dfrac{c−d}{d}$ .

¿Y si te dijeran que un modelo a escala de una pitón está en la proporción de 1:24? Si el modelo mide 0.75 pies de largo, ¿cuánto dura la pitón real?

Ejemplo $\PageIndex{1}$

En la imagen, $\dfrac{AB}{XY}=\dfrac{BC}{YZ}=\dfrac{AC}{XZ}$ .

Encuentra las medidas de $AC$ y $XY$ .

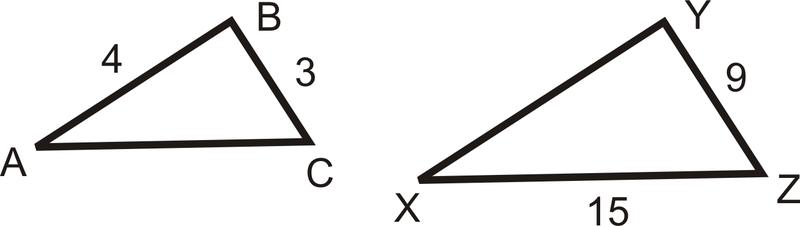
F-D_59AC68ADD548127DFF1E85A57D05CA413AA64908659A98CEAA229A9E+Image_Tiny+Image_Tiny.png — Figura $\PageIndex{1}$

Solución

Enchufe las longitudes de los lados que conocemos.

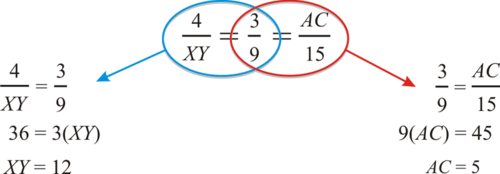
Ejemplo $\PageIndex{2}$

En la imagen, $\dfrac{AB}{BE}=\dfrac{AC}{CD}$ . Encuentra $BE$ .

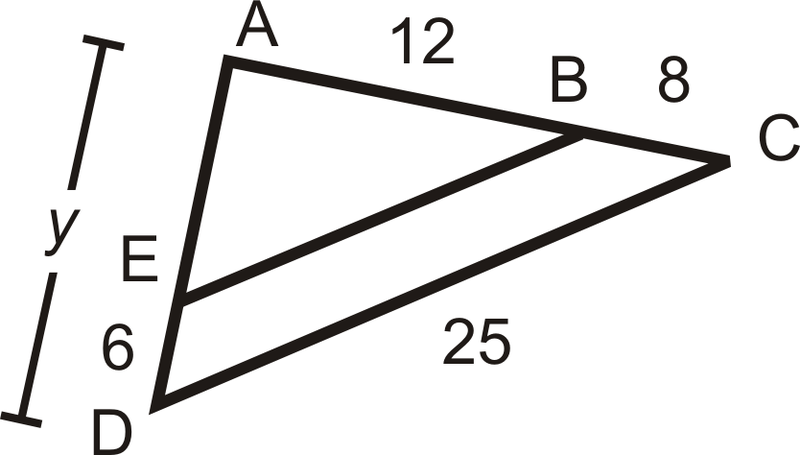
f-d_45eff6ef74834d8ca70cd2a370e28dffda281c051575892ecaa35378+image_tiny+image_tiny.png — Figura $\PageIndex{3}$

Solución

Sustituto en las longitudes de los lados que conocemos.

$\begin{aligned} \dfrac{12}{BE}=\dfrac{20}{25} \rightarrow 20(BE)&=12(25)\\ BE&=15\end{aligned}$

Ejemplo $\PageIndex{3}$

Resuelve las proporciones. Recuerda, para resolver una proporción, necesitas multiplicar de manera cruzada.

$\dfrac{4}{5}=\dfrac{x}{30}$
$\dfrac{y+1}{8}=\dfrac{5}{20}$
$\dfrac{6}{5}=\dfrac{2x+4}{x−2}$

Solución

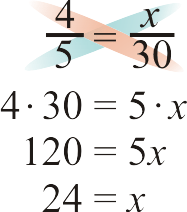
Figura $\PageIndex{4}$
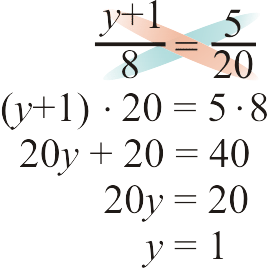
Figura $\PageIndex{5}$
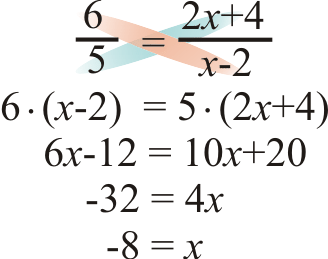
Figura $\PageIndex{6}$

Ejemplo $\PageIndex{4}$

Tus padres tienen un dibujo de arquitecto de su casa. En el papel, las dimensiones de la casa son 36 pulgadas por 30 pulgadas. Si la longitud más corta de la casa es en realidad de 50 pies, ¿cuál es la longitud más larga?

Solución

Para resolver, primero establecer una proporción. Si la longitud más corta es de 50 pies, entonces se alineará con 30 pulgadas, la longitud más corta de las dimensiones del papel.

$\begin{aligned}\dfrac{30}{3}6=\dfrac{50}{x} \rightarrow 30x&=1800 \\ x&=60 \qquad \text{The longer length is 60 feet.}\end{aligned}$

Ejemplo $\PageIndex{5}$

Supongamos que tenemos la proporción $\dfrac{2}{5}=\dfrac{14}{35}$ . Escribe tres proporciones verdaderas que siguen.

Solución

En primer lugar, sabemos que esta es una verdadera proporción porque se multiplicarían $\dfrac{2}{5}$ por $\dfrac{7}{7}$ para obtener $\dfrac{14}{35}$ . Usando los tres primeros corolarios:

$\dfrac{2}{14}=\dfrac{5}{35}$
$\dfrac{35}{5}=\dfrac{14}{2}$
$\dfrac{5}{2}=\dfrac{35}{14}$

Revisar

Resuelve cada proporción.

$\dfrac{x}{10}=\dfrac{42}{35}$
$\dfrac{x}{x−2}=\dfrac{5}{7}$
$\dfrac{6}{9}=\dfrac{y}{24}$
$\dfrac{x}{9}=\dfrac{16}{x}$
$\dfrac{y−3}{8}=\dfrac{y+6}{5}$
$\dfrac{20}{z+5}=\dfrac{16}{7}$
Shawna condujo 245 millas y usó 8.2 galones de gasolina. Al mismo ritmo, si manejaba 416 millas, ¿cuántos galones de gasolina necesitará? Redondear a la décima más cercana.
El presidente, vicepresidente y funcionario financiero de una empresa dividen las ganancias es una proporción 4:3:2. Si la empresa hizo $1,800,000 el año pasado, ¿cuánto recibió cada persona?

Dada la verdadera proporción, $\dfrac{10}{6}=\dfrac{15}{d}=\dfrac{x}{y}$ y $d$ $x$ , y $y$ son distintas de cero, determinar si las siguientes proporciones también son verdaderas.

$\dfrac{10}{y}=\dfrac{x}{6}$
$\dfrac{15}{10}=\dfrac{d}{6}$
$\dfrac{6+10}{10}=\dfrac{y+x}{x}$
$\dfrac{15}{x}=\dfrac{y}{d}$

Para las preguntas 13-16, $\dfrac{AE}{ED}=\dfrac{BC}{CD}$ y $\dfrac{ED}{AD}=\dfrac{CD}{DB}=\dfrac{EC}{AB}$ .

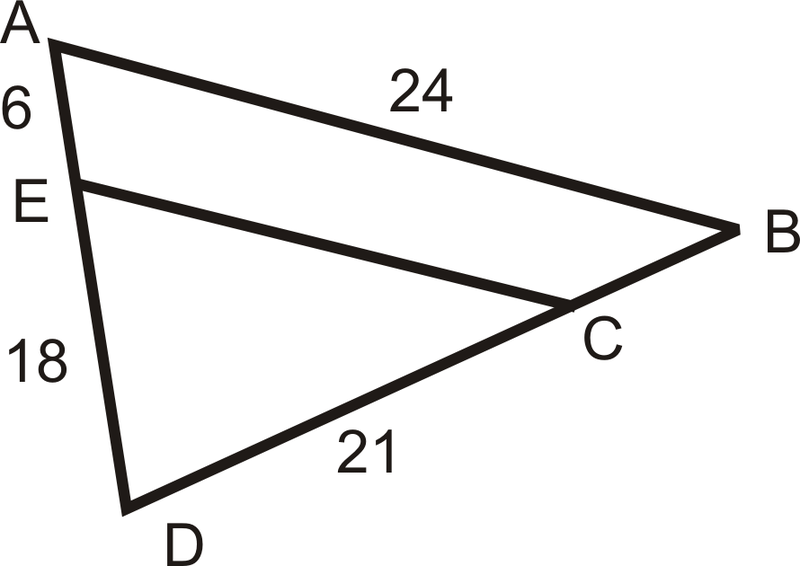
f-d_443ead3096e684bcf91e7531c10ed626ca50f63b885624bb24eaaa03+image_tiny+image_tiny.png — Figura $\PageIndex{7}$

Encuentra DB.
Encuentra EC.
Encuentra CB.
Encuentra AD.

Recursos

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.2.

El vocabulario

Término	Definición
corolario	Un teorema que sigue directamente de otro teorema.
proporción	Dos proporciones que se establecen iguales entre sí.
relación	Una manera de comparar dos números. Los ratios se pueden escribir de tres maneras:\ dfrac {a} {b}, a:b, y de a a a b.
Productos cruzados	Para simplificar una proporción usando productos cruzados, multiplique las diagonales de cada ratio.
Teorema de Multiplicación Cruzada	El teorema de multiplicación cruzada establece que si $a$ $b$ ,, $c$ y $d$ son números reales, con $b\neq 0$ y $d\neq 0$ y si $\dfrac{a}{b}=\dfrac{c}{d}$ , entonces $\dfrac{a}{d}=\dfrac{b}{c}$ .

Recursos adicionales

Elemento Interactivo

Video: Ratios

Actividades: Formas de Ratios Preguntas de Discusión

Ayudas de estudio: Guía de estudio de proporciones y proporciones

Práctica: Relación y Proporción en Cifras Similares

Mundo real: En la casa de muñecas

Proporciones

Revisar

Recursos

Reseña (Respuestas)

El vocabulario

Recursos adicionales

Support Center

How can we help?