7.3: Polígonos y Factores de Escala Similares
- Page ID
- 107435
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Polígonos similares
Polígonos similares son dos polígonos con la misma forma, pero no del mismo tamaño. Polígonos similares tienen ángulos correspondientes que son congruentes, y lados correspondientes que son proporcionales.
Estos polígonos no son similares:
Factores de Escala
Piense en polígonos similares como agrandar o encoger la misma forma. El símbolo\ sim\) se utiliza para representar similitud. Los tipos específicos de triángulos, cuadriláteros y polígonos siempre serán similares. Por ejemplo, todos los triángulos equiláteros son similares y todos los cuadrados son similares . Si dos polígonos son similares, sabemos que las longitudes de los lados correspondientes son proporcionales. En polígonos similares, la relación de un lado de un polígono al lado correspondiente del otro se denomina factor de escala. La relación de todas las partes de un polígono (incluyendo los perímetros, diagonales, medianas, segmentos medios, altitudes) es la misma que la relación de los lados.
Y si te dijeran que dos pentágonos eran similares y te dieran las longitudes de los lados de cada pentágono. ¿Cómo se podría determinar el factor de escala del pentágono #1 al pentágono #2?
Ejemplo\(\PageIndex{1}\)
\(ABCD\)y\(UVWX\) están abajo. ¿Estos dos rectángulos son similares?
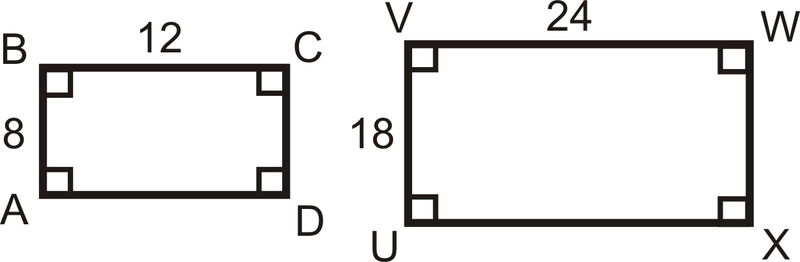
Solución
Todos los ángulos correspondientes son congruentes porque las formas son rectángulos.
Veamos si los lados son proporcionales. \(\dfrac{8}{12}=\dfrac{2}{3}\)y\(\dfrac{18}{24}=\dfrac{3}{4}\). \(\dfrac{2}{3}\neq \dfrac{3}{4}\), por lo que los lados no están en la misma proporción, y los rectángulos no son similares.
Ejemplo\(\PageIndex{2}\)
\(\Delta ABC\sim \Delta MNP\). El perímetro de\(\Delta ABC\) es de 150,\(AB=32\) y\(MN=48\). Encuentra el perímetro de\(\Delta MNP\).
Solución
De la declaración de similitud,\(AB\) y\(MN\) son lados correspondientes. El factor de escala es\(\dfrac{32}{48}=\dfrac{2}{3}\) o\(\dfrac{3}{2}\). \ Delta ABC\) es el triángulo más pequeño, por lo que el perímetro de\(\Delta MNP\) es\(\dfrac{3}{2}(150)=225\).
Ejemplo\(\PageIndex{3}\)
Supongamos\(\Delta ABC\sim \Delta JKL\). Con base en la declaración de similitud, ¿qué ángulos son congruentes y qué lados son proporcionales?
Solución
Al igual que en una declaración de congruencia, los ángulos congruentes se alinean dentro de la declaración de similitud. Entonces,\(\angle A\cong \angle J\),\(\angle B\cong \angle K\), y\ ángulo C\ cong\ ángulo L\). Escribe los lados en una proporción:\(\dfrac{AB}{JK}=\dfrac{BC}{KL}=\dfrac{AC}{JL}\). Tenga en cuenta que la proporción podría escribirse de diferentes maneras. Por ejemplo, también\(\dfrac{AB}{BC}=\dfrac{JK}{KL}\) es cierto.
Ejemplo\(\PageIndex{4}\)
\(MNPQ \sim RSTU\). ¿Cuáles son los valores de\(x\),\(y\) y\(z\)?
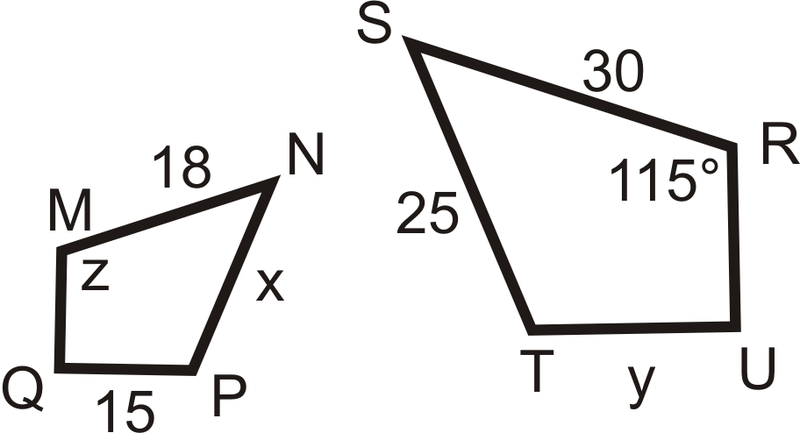
Solución
En la declaración de similitud,\(\angle M\cong \angle R\), entonces\(z=115^{\circ}\). Para\(x\) y\(y\), establecer proporciones.
\(\dfrac{18}{30}=\dfrac{x}{25} \qquad \dfrac{18}{30}=\dfrac{15}{y}\)
\(450=30x \qquad 18y=450\)
\(x=15\qquad y=25\)
Ejemplo\(\PageIndex{5}\)
\(ABCD\sim AMNP\). Encuentra el factor de escala y la longitud de\(BC\).
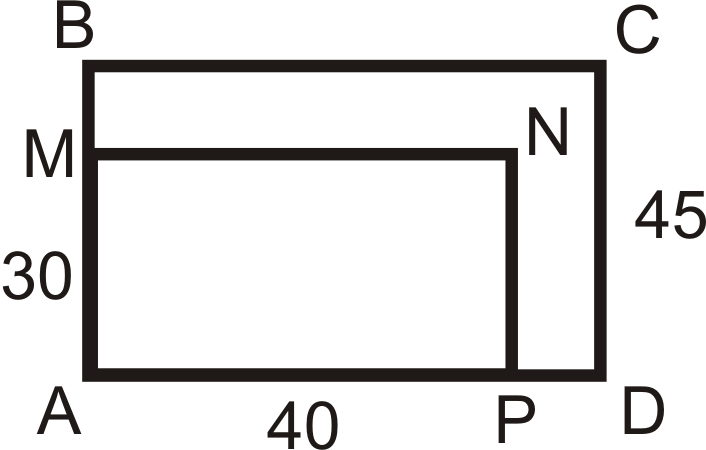
Solución
Alinee los lados correspondientes,\(AB\) y\(AM=CD\), así el factor de escala es\(\dfrac{30}{45}=\dfrac{2}{3}\) o\(\dfrac{3}{2}\). Porque\(BC\) está en el rectángulo más grande, vamos a multiplicar 40 por\(\dfrac{3}{2}\) porque\(\dfrac{3}{2}\) es mayor que 1. \(BC=\dfrac{3}{2}(40)=60\).
Revisar
Para las preguntas 1-8, determinar si las siguientes afirmaciones son verdaderas o falsas.
- Todos los triángulos equiláteros son similares.
- Todos los triángulos isósceles son similares.
- Todos los rectángulos son similares.
- Todos los rombos son similares.
- Todos los cuadrados son similares.
- Todos los polígonos congruentes son similares.
- Todos los polígonos similares son congruentes.
- Todos los pentágonos regulares son similares.
- \(\Delta BIG \sim \Delta HAT\). Enumere los ángulos congruentes y proporciones para los lados.
- Si\(BI=9\) y\(HA=15\), encuentra el factor de escala.
- Si\(BG=21\), encuentra\(HT\).
- Si\(AT=45\), encuentra\(IG\).
- Encuentra el perímetro de\(\Delta BIG\) y\(\Delta HAT\). ¿Cuál es la relación de los perímetros?
- Una cancha de basquetbol de la NBA es un rectángulo que mide 94 pies por 50 pies. Una cancha de basquetbol de secundaria es un rectángulo que mide 84 pies por 50 pies. ¿Los dos rectángulos son similares?
- Los televisores HD tienen lados en una proporción de 16:9. Los televisores que no son HD tienen lados en una proporción de 4:3. ¿Estas dos proporciones son equivalentes?
Usa la imagen de la derecha para responder a las preguntas 16-20.
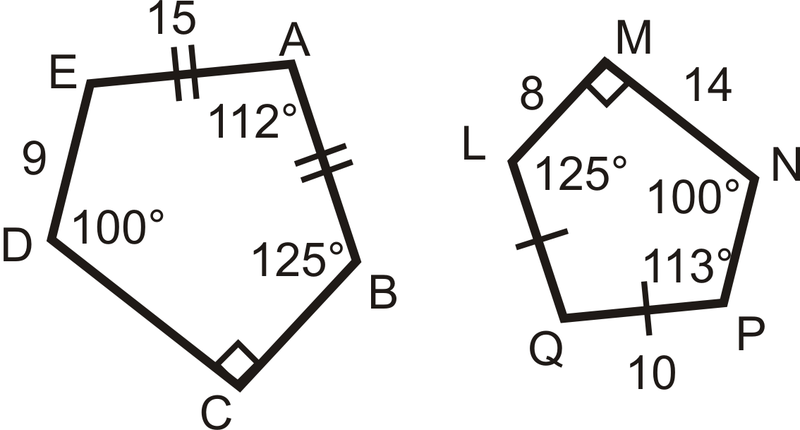
- Encontrar\(m\angle E\) y\(m\angle Q\).
- \(ABCDE\sim QLMNP\), encuentra el factor de escala.
- Encuentra BC.
- Encuentra CD.
- Encuentra NP.
Determinar si los siguientes triángulos y cuadriláteros son similares. Si lo son, escriba la declaración de similitud.
-
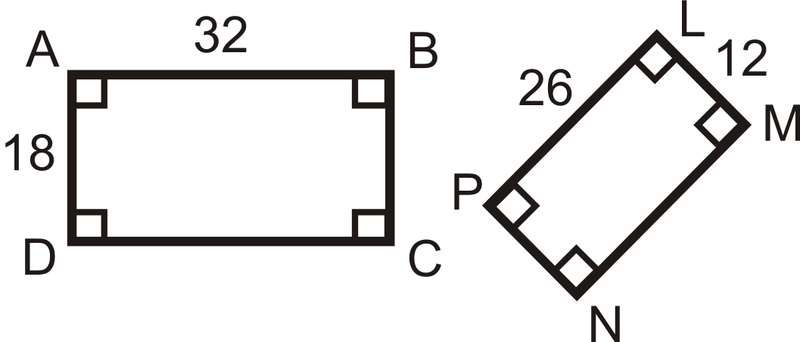
Figura\(\PageIndex{7}\) -
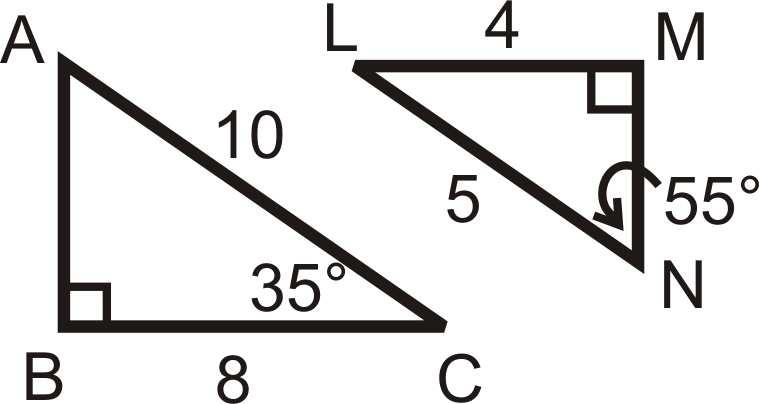
Figura\(\PageIndex{8}\) -
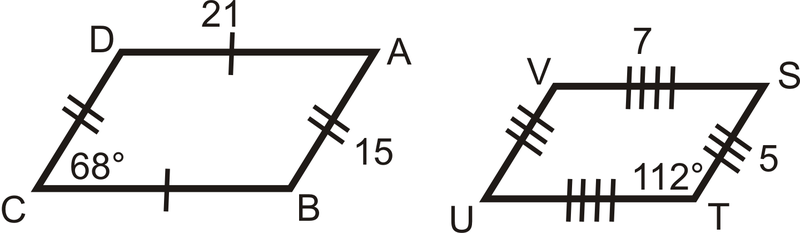
Figura\(\PageIndex{9}\) -
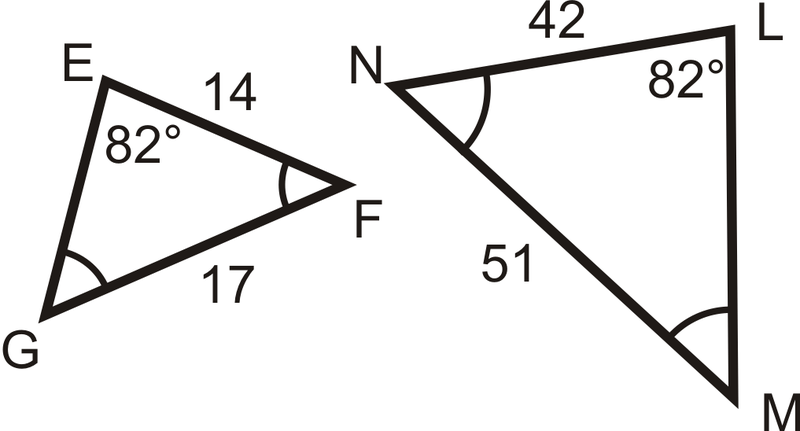
Figura\(\PageIndex{10}\) -
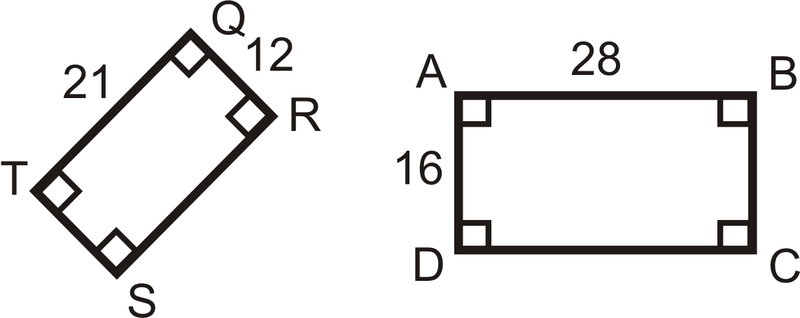
Figura\(\PageIndex{11}\) -
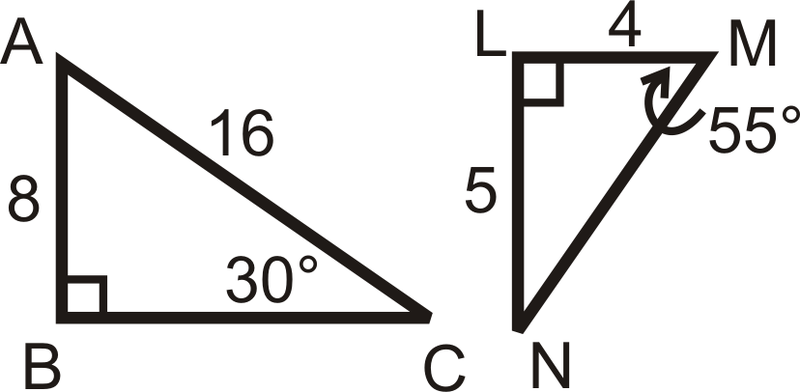
Figura\(\PageIndex{12}\) -
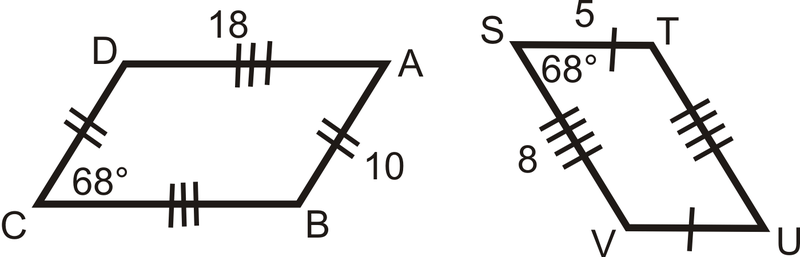
Figura\(\PageIndex{13}\) -
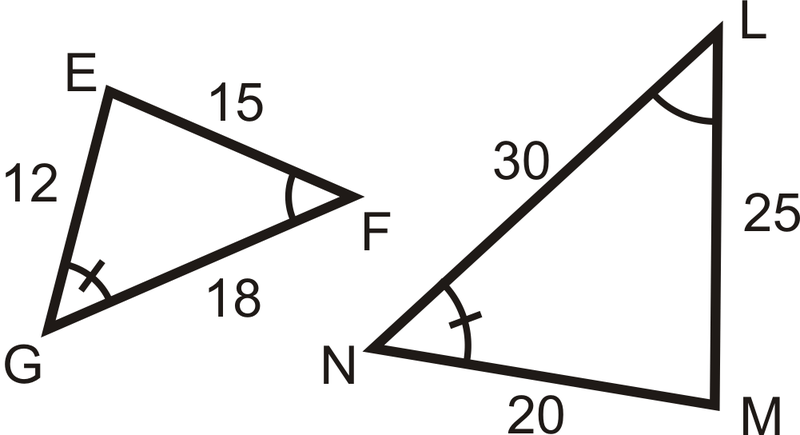Figura\(\ PageIndex {14}\) -
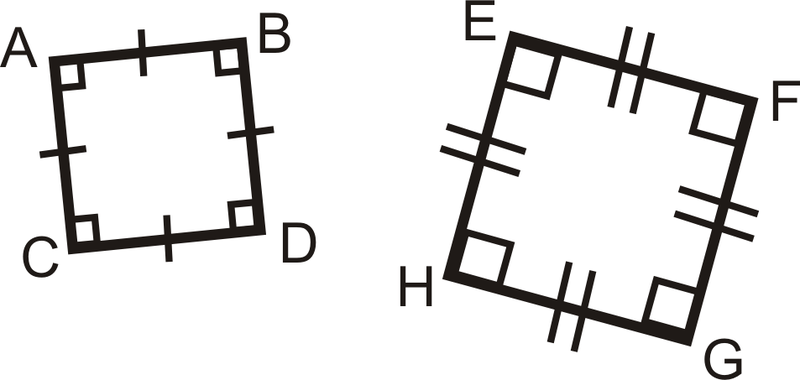
Figura\(\PageIndex{15}\) -
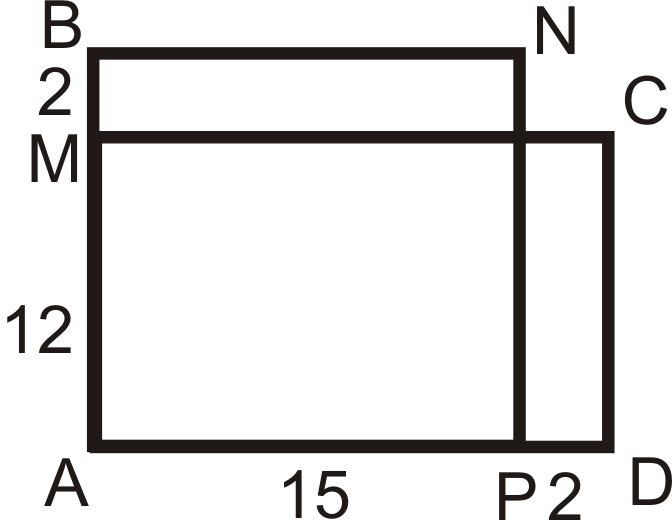
Figura\(\PageIndex{16}\)
Recursos
El vocabulario
| Término | Definición |
|---|---|
| polígonos similares | Dos polígonos con la misma forma, pero no del mismo tamaño. Los ángulos correspondientes de polígonos similares son congruentes (exactamente iguales) y los lados correspondientes son proporcionales (en la misma proporción). En polígonos similares, la relación de un lado de un polígono al lado correspondiente del otro se denomina factor de escala. |
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| Proporción | Una proporción es una ecuación que muestra dos proporciones equivalentes. |
| Factor de Escala | Un factor de escala es una relación entre la escala y la dimensión original o real escrita en la forma más simple. |
| seno | El seno de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado opuesto al ángulo dado por la longitud de la hipotenusa. |
| Relaciones trigonométricas | Proporciones que nos ayudan a entender las relaciones entre lados y ángulos de triángulos rectos. |