7.13: Proporciones y Bisectores de Ángulo
- Page ID
- 107414
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los bisectores angulares dividen los triángulos proporcionalmente.
Teorema de bisectriz angular
Cuando un ángulo dentro de un triángulo es biseccionado, la bisectriz divide el triángulo proporcionalmente. Esta idea se llama Teorema de Bisectriz Angular.
Teorema de Bisectriz Angular: Si un rayo bisecta un ángulo de un triángulo, entonces divide el lado opuesto en segmentos que son proporcionales a las longitudes de los otros dos lados.
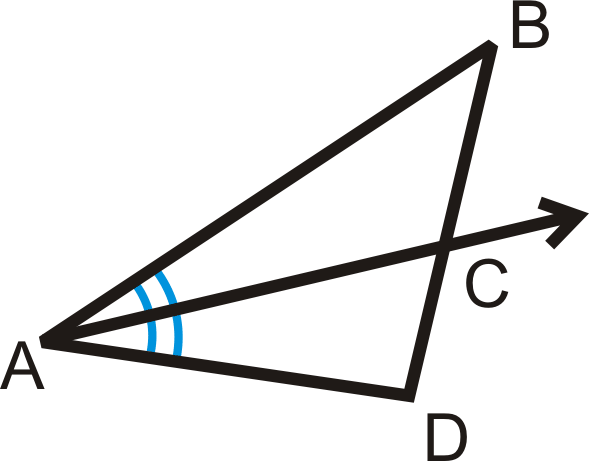
Si\(\Delta BAC\cong \Delta CAD\), entonces\(\dfrac{BC}{CD}=\dfrac{AB}{AD}\).
¿Y si te dijeran que un rayo era un ángulo bisectriz de un triángulo? ¿Cómo usarías este hecho para encontrar valores desconocidos respecto a las longitudes de los lados del triángulo?
Ejemplo\(\PageIndex{1}\)
Rellene la variable que falta:
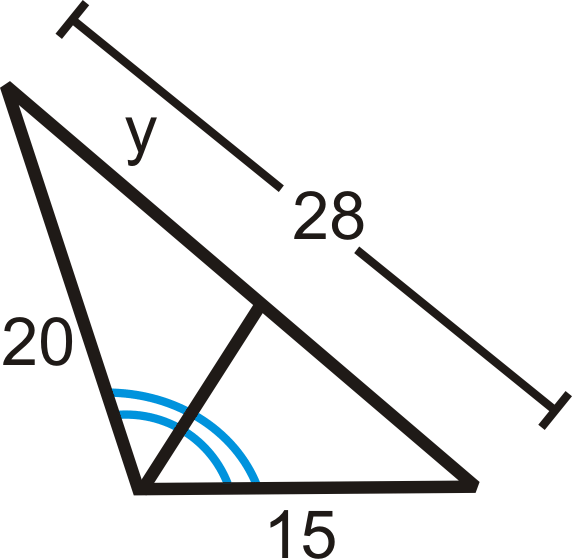
Solución
Establecer una proporción y resolver.
\(\begin{aligned} \dfrac{20}{y}&=\dfrac{15}{28−y} \\ 15y&=20(28−y) \\ 15y&=560−20y \\ 35y&=560 \\ y&=16\end{aligned}\)
Ejemplo\(\PageIndex{2}\)
Rellene la variable que falta:
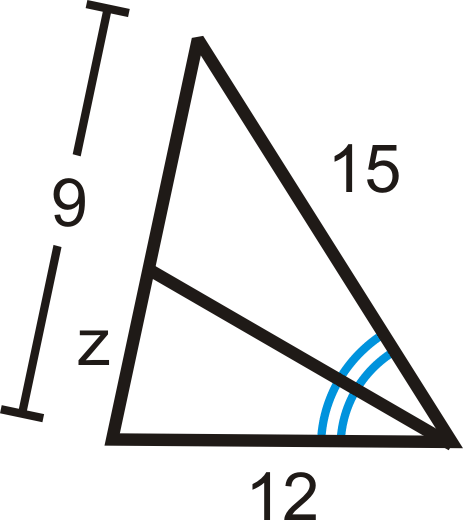
Solución
Establecer una proporción y resolver.
\(\begin{aligned}\dfrac{12}{z}&=\dfrac{15}{9−z} \\ 15z&=12(9−z) \\ 15z&=108-12z \\ 27z&=108 \\ z&=4\end{aligned}\)
Ejemplo\(\PageIndex{3}\)
Encuentra\(x\).
Solución
El rayo es el ángulo bisectriz y divide el lado opuesto en la misma proporción que los otros dos lados. La proporción es:
\(\begin{aligned} \dfrac{9}{x}&=\dfrac{21}{14} \\ 21x&=126 \\ x&=6\end{aligned}\)
Ejemplo\(\PageIndex{4}\)
Encontrar el valor de\(x\) eso haría verdadera la proporción.
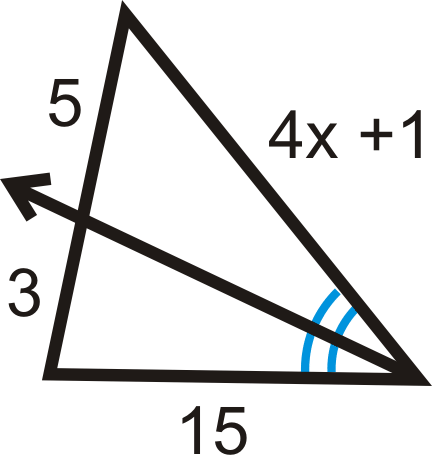
Solución
Se puede configurar esta proporción como el ejemplo anterior.
\(\begin{aligned} \dfrac{5}{3}&=\dfrac{4x+1}{15} \\ 75&=3(4x+1) \\ 75&=12x+3 \\ 72&=12x \\ 6&=x\end{aligned}\)
Ejemplo\(\PageIndex{5}\)
Encuentra la variable que falta:
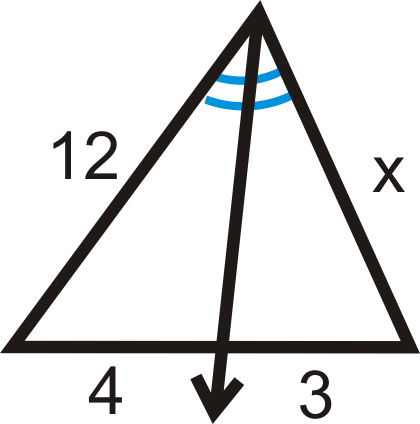
Solución
Configura una proporción y resuelve como en los ejemplos anteriores.
\(\begin{aligned}\dfrac{12}{4}&=\dfrac{x}{3} \\ 36&=4x \\ x&=9\end{aligned}\)
Revisar
Encuentra el valor de las variables faltantes.
-
Figura\(\PageIndex{7}\) -
Figura\(\PageIndex{8}\)
Resolver para la variable desconocida.
-
Figura\(\PageIndex{9}\) -
Figura\(\PageIndex{10}\) -
Figura\(\PageIndex{11}\) -
Figura\(\PageIndex{12}\) -
Figura\(\PageIndex{13}\) -
Figura\(\PageIndex{14}\) -
Figura\(\PageIndex{15}\) -
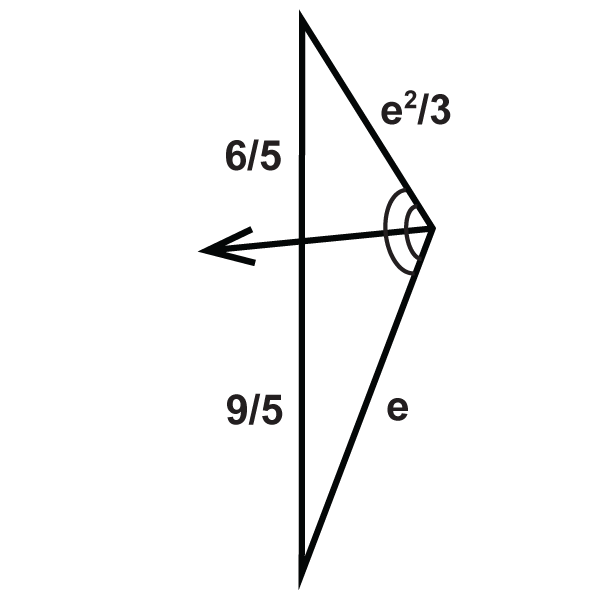
Figura\(\PageIndex{16}\) -
Figura\(\PageIndex{17}\) -
Figura\(\PageIndex{18}\) -
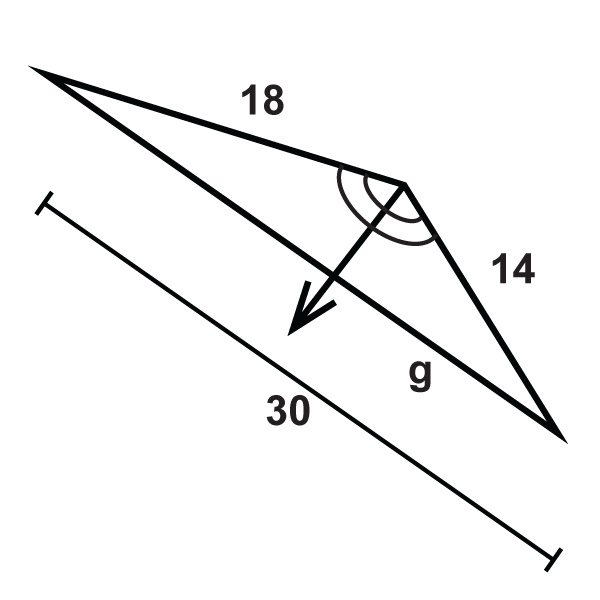
Figura\(\PageIndex{19}\) -
Figura\(\PageIndex{20}\) -
Figura\(\PageIndex{21}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.10.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| bisectriz angular | Un rayo que divide un ángulo en dos ángulos congruentes. |
| Teorema de bisectriz angular | El teorema de la bisectriz del ángulo establece que si un punto está en la bisectriz de un ángulo, entonces el punto es equidistante de los lados del ángulo. |
| Proporción | Una proporción es una ecuación que muestra dos proporciones equivalentes. |
| Ratio | Una relación es una comparación de dos cantidades que se pueden escribir en forma de fracción, con dos puntos o con la palabra “a”. |
Recursos adicionales
Elemento interactivo
Video: Uso de las propiedades del teorema de bisectriz de ángulo triangular para determinar valores desconocidos
Actividades: Proporciones con bisectores angulares Preguntas de discusión
Ayudas de estudio: Guía de estudio de relaciones de proporcionalidad
Mundo real: proporcionalidad triangular