7.6: Aplicaciones de medición indirecta
- Page ID
- 107428
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Usa proporciones y proporciones para resolver longitudes faltantes en figuras similares en situaciones del mundo real.
Medición Indirecta
Una aplicación de triángulos similares es medir longitudes indirectamente. Se puede utilizar este método para medir el ancho de un río o cañón o la altura de un objeto alto. La idea es que modele una situación con triángulos similares y luego use proporciones para encontrar la medida faltante de manera indirecta.
¿Y si estuvieras parado junto a un edificio y quisieras saber qué tan alto es el edificio? ¿Cómo podrías usar tu propia altura y la longitud de las sombras proyectadas por ti y el edificio para determinar la altura del edificio?
Para los Ejemplos 1, 2 y 3, utilice la siguiente información:
Para estimar el ancho de un río, se puede utilizar la siguiente técnica. Usa el diagrama.
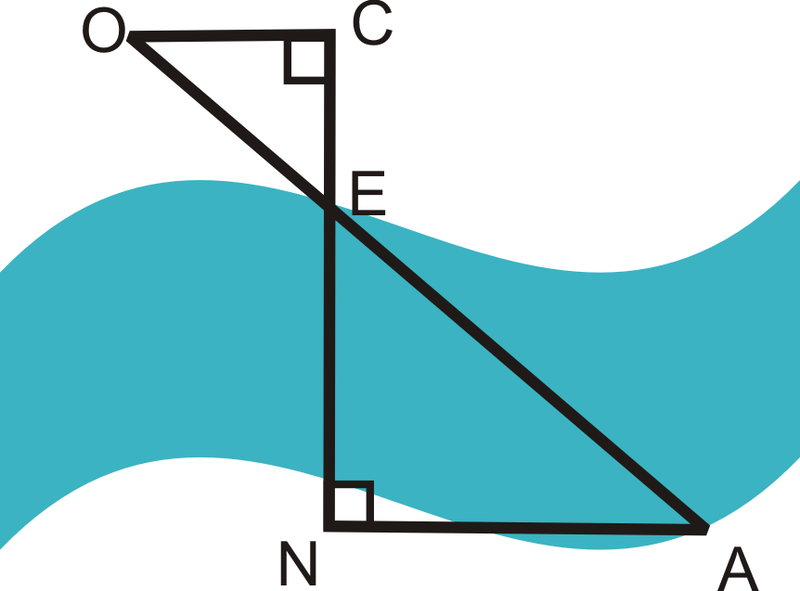
Colocar tres marcadores\(O\),\(C\),, y\(E\) en la orilla superior del río. \(E\)está a la orilla del río y\(\overline{OC}\perp \overline{CE}\). Cruza el río y coloca un marcador,\(N\) para que quede colineal con\(C\) y\(E\). Después, caminar por la orilla inferior del río y colocar el marcador A\), para que\(\overline{CN}\perp \overline{NA}\). \(OC=50 feet\),\(CE=30\: feet\),\(NA=80\: feet\).
Ejemplo\(\PageIndex{1}\)
¿Es\(\Delta OCE\sim \Delta ANE\)? ¿Cómo lo sabes?
Solución
Sí. \(\angle C\cong \angle N\)porque ambos son ángulos rectos. \(\angle OEC\cong \angle AEN\)porque son ángulos verticales. Esto significa\(\Delta OCE\sim \Delta ANE\) por el Postulado de Similitud AA.
Ejemplo\(\PageIndex{2}\)
¿Es\(\overline{OC}\parallel \overline{NA}\)? ¿Cómo lo sabes?
Solución
Ya que los dos triángulos son similares, debemos tener\(\angle EOC\cong \angle EAN\). Estos son ángulos interiores alternos. Cuando los ángulos interiores alternos son congruentes entonces las líneas son paralelas, entonces\(\overline{OC}\parallel \overline{NA}\).
Ejemplo\(\PageIndex{3}\)
¿Cuál es el ancho del río? Encontrar\(EN\).
Solución
Configura una proporción y resuelve multiplicando de manera cruzada.
\(\dfrac{30\: ft}{EN}=\dfrac{50\: ft}{80\: ft}\)
\(50(EN)=2400\)
\(EN=48\)
El río tiene 48 pies de ancho.
Ejemplo\(\PageIndex{4}\)
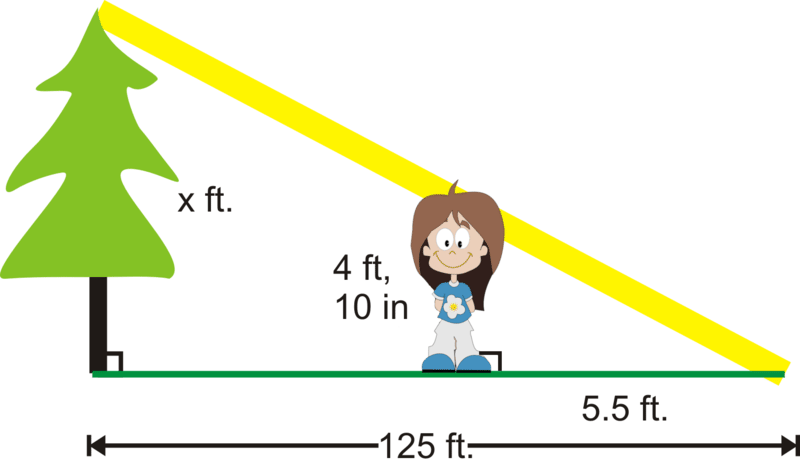
Un árbol afuera del edificio de Ellie proyecta una sombra de 125 pies. A la misma hora del día, Ellie proyecta una sombra de 5.5 pies. Si Ellie mide 4 pies y 10 pulgadas de alto, ¿qué tan alto es el árbol?
Solución
Para resolver, comience por dibujar un cuadro. Vemos que el árbol y Ellie son paralelos, por lo que los dos triángulos son similares.
\(\dfrac{4\: ft,10\: in}{x}=\dfrac{5.5\: ft}{125\: ft}\)
Las mediciones deben ser en las mismas unidades. Cambiar todo en pulgadas y luego podemos cruzar multiplicar.
\(\dfrac{58\: in}{x}=\dfrac{66\: in}{1500\: in}\)
\(87000=66x\)
\(x\approx 1318.\overline{18} in or 109.85\: ft\)
Ejemplo\(\PageIndex{5}\)
Cameron mide 5 pies de altura y proyecta una sombra de 12 pies. A la misma hora del día, un edificio cercano proyecta una sombra de 78 pies. ¿Qué tan alto es el edificio?
Solución
Para resolverlo, establezca una proporción que compare la altura con la longitud de la sombra para Cameron y el edificio. Entonces resuelve la ecuación para encontrar la altura del edificio. Dejar x representar la altura del edificio.
\ dfrac {5 pies} {12\: pies} =\ dfrac {x} {78\: pies}\)
12x=390\)
x=32.5\: ft\)
El edificio mide 32.5 pies de altura.
Revisar
Se utilizó la técnica de la sección de práctica guiada para medir la distancia a través del Gran Cañón. Usa la imagen de abajo y\(OC=72\: ft\)\(CE=65\: ft\),, y\(NA=14,400\: ft\) para problemas 1 - 3.

1. Encontrar\(EN\) (la distancia a través del Gran Cañón).
2. Encontrar\(OE\).
3. Encontrar\(EA\).
4. Mark mide 6 pies de altura y proyecta una sombra de 15 pies. A la misma hora del día, un edificio cercano proyecta una sombra de 30 pies. ¿Qué tan alto es el edificio?
5. Karen y Jeff están parados uno al lado del otro. Karen proyecta una sombra de 10 pies y Jeff proyecta una sombra de 8 pies. ¿Quién es más alto? ¿Cómo lo sabes?
6. Billy mide 5 pies y 9 pulgadas de alto y Bobby mide 6 pies de alto. La sombra de Bobby mide 13 pies de largo. ¿Cuánto dura la sombra de Billy?
7. Sally y su hermanito van caminando a la escuela. Sally mide 4 pies de altura y tiene una sombra de 3 pies de largo. La sombra de su hermano pequeño mide 2 pies de largo. ¿Qué tan alto es su hermanito?
8. Ryan está afuera jugando básquetbol. Mide 5 pies de altura y a esta hora del día está proyectando una sombra de 12 pies. El aro de básquetbol mide 10 pies de altura. ¿Cuánto dura la sombra del aro de basquetbol?
9. Jack está parado junto a un árbol muy alto y se pregunta qué tan alto es. Sabe que mide 6 pies de altura y en este momento su sombra mide 8 pies de largo. Mide la sombra del árbol y encuentra que mide 90 pies. ¿Qué tan alto es el árbol?
10. Thomas, que mide 4 pies y 9 pulgadas de alto, está proyectando una sombra de 6 pies. Un edificio cercano está proyectando una sombra de 42 pies. ¿Qué tan alto es el edificio?
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Postulado de similitud AA | Si dos ángulos en un triángulo son congruentes con dos ángulos en otro triángulo, entonces los dos triángulos son similares. |
| Proporción | Una proporción es una ecuación que muestra dos proporciones equivalentes. |
Recursos adicionales
Elemento Interactivo
Video: Escala y Mediciones Indirectas
Actividades: Preguntas de Discusión de Medición Indirecta
Ayudas de estudio: Guía de estudio de similitud poligonal
Práctica: Aplicaciones de medición indirecta
Mundo real: Mediciones poderosas

