7.5: Medición indirecta
- Page ID
- 107447
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Encuentra longitudes usando proporciones de triángulos similares.
Medidas Desconocidas de Cifras Similares

El padre de Shelby es un ex nadador olímpico. Le encanta nadar, pero no puede construir una piscina de tamaño olímpico en su patio trasero porque no tiene el espacio. Decide construir una alberca más pequeña que sea similar a las dimensiones de una alberca olímpica. Una alberca olímpica tiene una longitud de 50 metros y una anchura de 25 metros. Su alberca tiene una longitud de 25 metros. ¿Cuál es el ancho de su alberca?
En este concepto, aprenderás a encontrar las medidas desconocidas de figuras similares.
Encontrar medidas desconocidas de cifras similares
Si conoces la longitud de un lado en una figura, puedes usar el factor de escala para encontrar la medida del lado correspondiente en una figura similar. Veamos cómo funciona esto.
Lado a en triángulo ABC corresponde al lado x en el triángulo menor XYZ. El lado x tiene 4 metros de largo y el factor de escala es 6. ¿Cuál es la medida del lado a?
Se le ha dicho que dos lados, a y x, corresponden en un pequeño triángulo y uno grande. El lado x tiene 4 metros de largo, y el factor de escala te indica que el lado a será seis veces más largo. Escribamos esto y resolvamos.
\(\text{side} x \times \text{ scale factor }=\text{ side }\: a\)
\(4\times 6=\text{ side a }\)
\(24 \text{ m }=\text{ side a }\)
Lado a debe tener una longitud de 24 metros.
Puede verificar configurando una relación que compare las longitudes de los dos lados. Si el factor de escala es 6, entonces su trabajo es preciso.
\(\dfrac{a}{x}=\dfrac{24}{4}=6\)
En ocasiones, puedes averiguar las longitudes laterales faltantes observando las medidas dadas. Siempre mire el diagrama de las figuras y vea si puede determinar la longitud faltante sin medir.
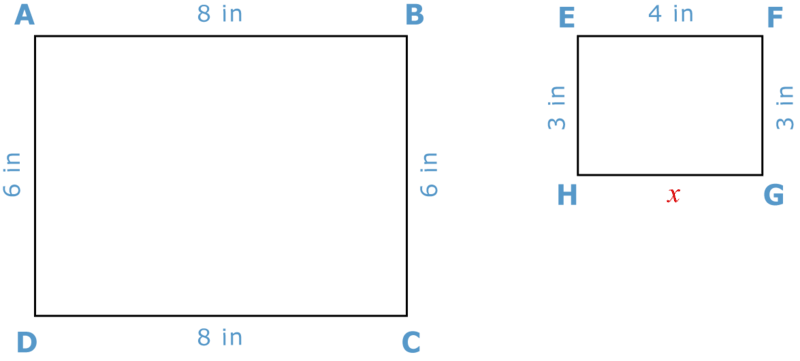
Mira estos dos rectángulos. Primero, mira y mira si puedes averiguar la relación entre las dos figuras. Para ello, se comparan las longitudes laterales de cada parte de las dos figuras.
Es necesario averiguar la medida del lado GH en el segundo rectángulo.
Se puede ver que las medidas en el segundo rectángulo son la mitad de grandes que las medidas en el primero. Además, sabes que los lados opuestos de un rectángulo son congruentes. Por lo tanto, la longitud lateral faltante es 4.
Figuras similares que se relacionan por un factor de escala a menudo se ven en mapas, planos arquitectónicos y diagramas. En la mayoría de estos casos, se da el factor de escala para que sepas agrandar los ítems del dibujo a sus tamaños reales. Eche un vistazo al plano de planta a continuación. Se muestra dónde se encuentra el mobiliario en una sala de estar.
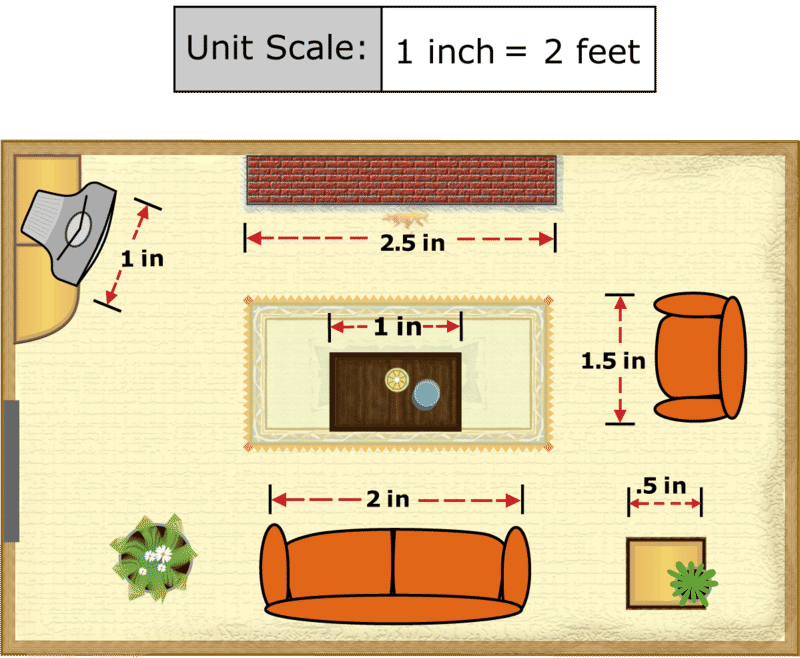
Te dice que una pulgada en el dibujo es igual a dos pies de tamaño real. Por lo tanto, si conoce el tamaño en pulgadas de cualquier objeto en el plano de planta, puede encontrar su tamaño real en pies. Vamos a probarlo.
Encuentra el sofá en el plano de planta y luego encuentra su longitud en pulgadas. El sofá en el plano de planta mide 2 pulgadas de largo. Esto es como conocer la longitud de un lado en una figura similar. Ahora usa el factor de escala como lo harías para encontrar la longitud del lado correspondiente en una figura similar (en este caso el “lado correspondiente” es el sofá real). Simplemente multiplica la longitud que conoces por el factor de escala:
\(\text{ sofa drawing }\times \text{ scale factor }=\text{ actual sofa size }\)
\(2\text{ inches }\times 2=4 \text{ feet }\)
El sofá mide 4 pies de largo.
A continuación, calculemos la longitud real de la chimenea.Usa una regla para medir la chimenea en el dibujo. Tiene 2.5 pulgadas de largo. Multiplique esto por el factor de escala para encontrar la longitud en pies.
\(\text{ fireplace drawing }\times \text{ scale factor }=\text{ actual fireplace length }\)
\(2.5\text{ inches}\times 2=5 \text{ feet }\)
La longitud real de la chimenea es de 5 pies.
También puedes revertir el proceso para tomar un tamaño real y reducirlo.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre el padre de Shelby y su piscina.
Construye una alberca que es similar a una alberca olímpica. Una alberca olímpica tiene una longitud de 50 metros y una anchura de 25 metros. Si su alberca tiene una longitud de 25 metros, ¿cuál es el ancho de su alberca?
Solución
Primero, establecer una ecuación que pueda ser utilizada para resolver por el ancho de su piscina.
\(\dfrac{50}{25}=\dfrac{25}{x}\)
A continuación, cruzar multiplicar.
\(50x=625\)
Después, divida ambos lados de la ecuación por 50.
\(x= 12.5\)
La respuesta es que su alberca tiene un ancho de 12.5 metros.
Ejemplo\(\PageIndex{2}\)
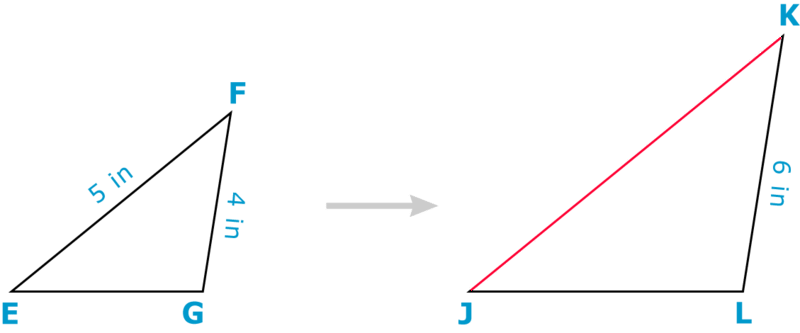
Utilice el factor de escala de las cifras similares a continuación para encontrar la medida de KJ.
Solución
Primero, establecer una proporción para resolver por el lado faltante.
\(\dfrac{KJ}{5}=\dfrac{6}{4}\)
Esta proporción se escribe de manera que los lados correspondientes formen las dos proporciones de la proporción. Se puede decir que\(KJ\) es lo desconocido en esta proporción.
A continuación, cruzar multiplicar.
\(\begin{aligned} KJ\times 4&=4KJ \\ 5\times 6&=30 \\ 4KJ&=30\end{aligned}\)
Luego resuelve la ecuación para KJ dividiendo ambos lados de la ecuación por 4.
\(\begin{aligned} 30\divide 4&=7.5 \\ KJ&=7.5 \end{aligned}\)
La respuesta es que la longitud lateral de\(KJ\) es 7.5.
Ejemplo\(\PageIndex{3}\)
Chris está haciendo un dibujo de su escuela y los terrenos que la rodean. La cancha de basquetbol mide 75 pies de largo y 40 pies de ancho. Si Chris usa un factor de escala en el que 1 pulgada equivale a 10 pies, ¿cuáles deberían ser las dimensiones de la cancha de básquetbol en su dibujo?

Solución
Primero, escribe la información que conozcas.
El tamaño real de la cancha de basquetbol y el factor de escala que Chris está usando para su dibujo.
A continuación, establezca una ecuación para encontrar la longitud que Chris debería dibujar.
\(\begin{aligned} \text{ drawing length }\times \text{ scale factor }=\text{ actual basketball court length } \\ \text{ drawing length } \times 10=75 feet \\ \text{ drawing length }&=75\divide 10 \\ \text{ drawing length }&=7.5 \text{ inches }\end{aligned}\)
La longitud de la cancha de basquetbol en el dibujo de Chris debe ser de 7.5 pulgadas.
Entonces, usa el mismo proceso para encontrar el ancho que Chris debería dibujar.
\(\begin{aligned} \text{ drawing width } \times \text{ scale factor }=\text{ actual basketball court width }\\ \text{ drawing width } \times 10=40 \text{ feet } \\ \text{ drawing width }=40\divide 10 \\ \text{ drawing width }=4\text{ inches } \end{aligned}\)
La respuesta es que Chris debería representar la cancha de basquetbol como un rectángulo de 7.5 por 4 pulgadas en su dibujo.
Ejemplo\(\PageIndex{4}\)
Resolver para\(x\).
\(\dfrac{3}{4}=\dfrac{x}{12}\)
Solución
Primero, cruzar multiplicar.
\(4x = 36\)
A continuación, divida ambos lados de la ecuación por 4.
\(x = 9\)
Entonces, exponer la solución.
9
La respuesta es que\(x\) equivale a 9.
Ejemplo\(\PageIndex{5}\)
Resolver para\(x\).
\(\dfrac{3}{6}=\dfrac{1}{x}\)
Solución
Primero, cruzar multiplicar.
\(3x = 6\)
A continuación, divide ambos lados de la ecuación por 3.
\(x = 2\)
Entonces, exponer la solución.
2
La respuesta es que\(x\) equivale a 2.
Revisar
Resuelve cada problema.
- Lado\(m\) en triángulo\(LMN\) corresponde al lado c en el triángulo más pequeño\(BCD\). El lado m mide 12 cm de largo y el factor de escala es 4. ¿Cuál es la medida del lado c?
- Lado\(q\) en triángulo\(PQR\) corresponde al lado y en el triángulo más pequeño\(XYZ\). El lado y tiene 8 pulgadas de largo y el factor de escala es 7. ¿Cuál es la medida del lado q?
Resuelve cada proporción para la longitud lateral faltante.
- \(\dfrac{7}{10}=\dfrac{x}{30}\)
- \(\dfrac{1.5}{3}=\dfrac{x}{6}\)
Ahora usa el factor de escala para crear una nueva proporción.
- \(\dfrac{1}{3}\), factor de escala 4
- \(\dfrac{8}{5}\), factor de escala 5
- \(\dfrac{9}{3}\), factor de escala 3
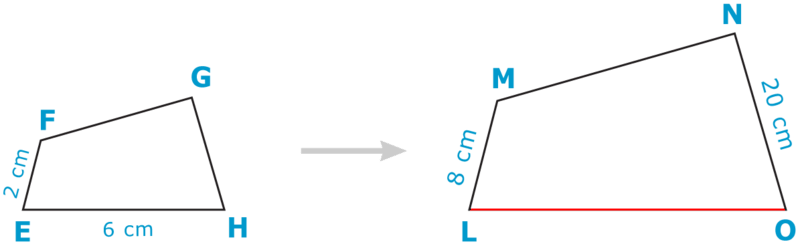
- Encuentre el factor de escala de las cifras similares a continuación y luego utilícelo para encontrar la medida de LO\).
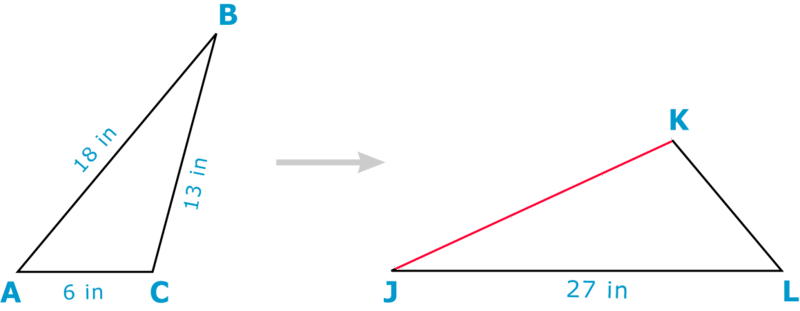
- Utilice el factor de escala de las cifras similares a continuación para encontrar la medida de\(JK\).
Usa el mapa de abajo y una regla para responder a las preguntas que siguen.
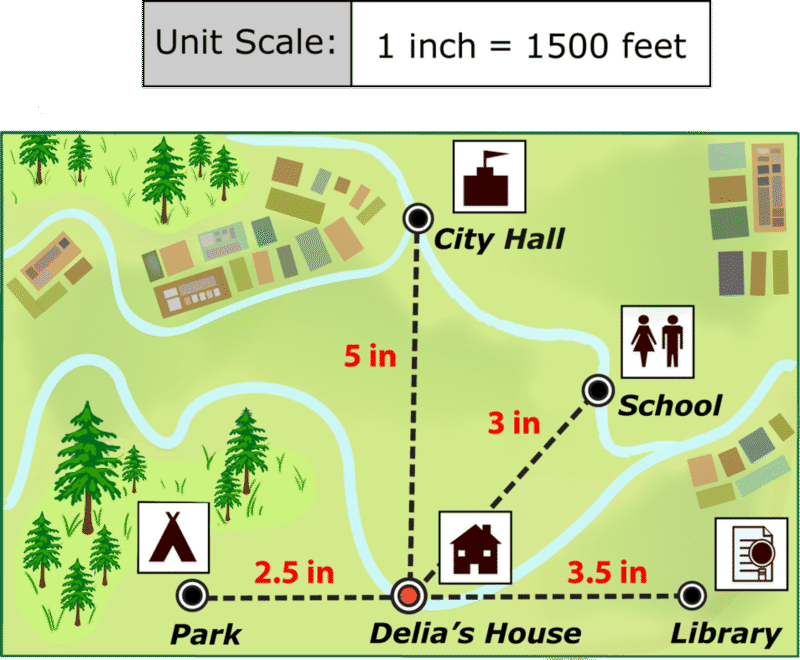
- ¿A qué distancia vive Delia de su escuela?
- ¿A qué distancia está la biblioteca del parque?
- ¿A cuánta distancia vive Delia del Ayuntamiento?
- Delia dibujó otro punto para mostrar la comisaría en su mapa. Ella lo dibujó a 1.5 pulgadas de distancia del Ayuntamiento. ¿Cuál es la distancia real entre la comisaría y el Ayuntamiento?
- ¿A qué distancia vive Delia del parque?
- ¿Qué tan lejos vive de la biblioteca?
- ¿Qué es lo más lejos que Delia viajará a cualquier artículo de su mapa?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.15.
Recursos
vocabulario
| Término | Definición |
|---|---|
| Medición Indirecta | La medición indirecta es el proceso de utilizar las características de triángulos similares para medir distancias. |
| Factor de Escala | Un factor de escala es una relación entre la escala y la dimensión original o real escrita en la forma más simple. |
| Similares | Dos figuras son similares si tienen la misma forma, pero no necesariamente del mismo tamaño. |
Recursos adicionales
Elemento Interactivo
Video: Triángulos Congruentes y Similares
Práctica: Medición indirecta
Mundo real: Mediciones poderosas

