7.8: Similitud de SSS
- Page ID
- 107469
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los triángulos son similares si sus lados correspondientes son proporcionales.
Teorema de similitud SSS
Por definición, dos triángulos son similares si todos sus ángulos correspondientes son congruentes y sus lados correspondientes son proporcionales. No es necesario revisar todos los ángulos y lados para saber si dos triángulos son similares. De hecho, si solo sabes que todos los lados son proporcionales, esa es información suficiente para saber que los triángulos son similares. Esto se llama Teorema de Similaridad SSS.
Teorema de similitud SSS: Si los tres pares de lados correspondientes de dos triángulos son proporcionales, entonces los dos triángulos son similares.
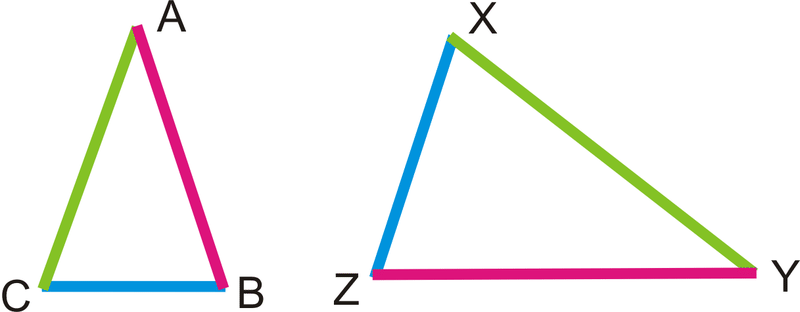
Si\(\dfrac{AB}{YZ}=\dfrac{BC}{ZX}=\frac{AC}{XY}\), entonces\(\Delta ABC\sim \Delta YZX\).
¿Y si te dieran un par de triángulos y las longitudes laterales para los tres lados? ¿Cómo podría usar esta información para determinar si los dos triángulos son similares?
Para los Ejemplos 1 y 2, utilice el siguiente diagrama:
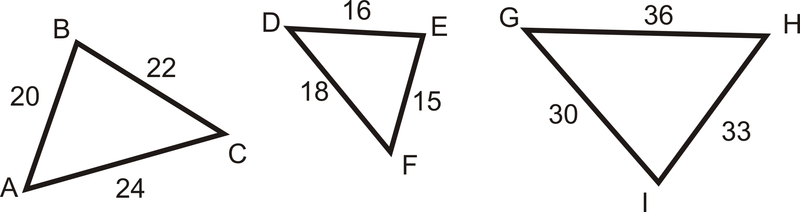
Ejemplo\(\PageIndex{1}\)
¿Es\(\Delta DEF\sim \Delta GHI\)?
¿Es\(\dfrac{15}{30}=\dfrac{16}{33}=\dfrac{18}{36}\)?
Solución
\(\dfrac{15}{30}=\dfrac{1}{2}\),\(\dfrac{16}{33}=\dfrac{16}{33}\), y\(\dfrac{18}{36}=\dfrac{1}{2}\). \(\dfrac{1}{2}\neq \dfrac{16}{33}\), no\(\Delta DEF\) es similar a\(\Delta GHI\).
Ejemplo\(\PageIndex{2}\)
¿Es\(\Delta ABC\sim \Delta GHI\)?
¿Es\(\dfrac{20}{30}=\dfrac{22}{33}=\dfrac{24}{36}\)?
Solución
\(\dfrac{20}{30}=dfrac{2}{3}\),\(\dfrac{22}{33}=\dfrac{2}{3}\), y\(\dfrac{24}{36}=\dfrac{2}{3}\). Las tres proporciones se reducen a\(\dfrac{2}{3}\),\(\Delta ABC\sim \Delta GHI\).
Ejemplo\(\PageIndex{3}\)
Determinar si los siguientes triángulos son similares. Si es así, explique por qué y escriba la declaración de similitud.
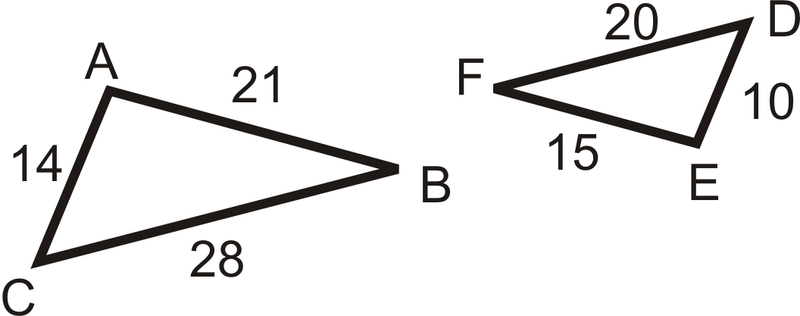
Solución
Habrá que encontrar las proporciones para los lados correspondientes de los triángulos y ver si todos son iguales. Comience con los lados más largos y trabaje hasta los lados más cortos.
\(\begin{aligned} \dfrac{BC}{FD}&=\dfrac{28}{20}=\dfrac{7}{5} \\ \dfrac{BA}{FE}&=\dfrac{21}{15}=\dfrac{7}{5} \\ \dfrac{AC}{ED}&=\dfrac{14}{10}=\dfrac{7}{5}\end{aligned}\)
Ya que todas las proporciones son iguales,\(\Delta ABC\sim \Delta EFD\) por el Teorema de Similitud de SSS.
Ejemplo\(\PageIndex{4}\)
Encuentra\(x and \(y, such that \(\Delta ABC\sim \Delta DEF\).
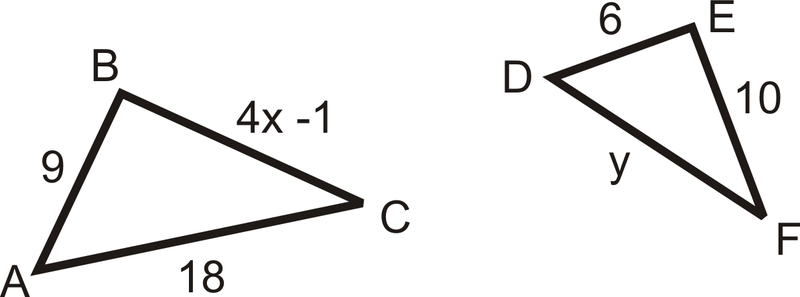
Solución
De acuerdo con la declaración de similitud, los lados correspondientes son:\(\dfrac{AB}{DE}=\dfrac{BC}{EF}=\dfrac{AC}{DF}\). Sustituyendo en lo que sabemos, tenemos\(\dfrac{9}{6}=\dfrac{4x−1}{10}=\dfrac{18}{y}\).
\ (\ begin {alineado}
\ frac {9} {6} &=\ frac {4 x-1} {10} &\ frac {9} {6} &=\ frac {18} {y}\\
9 (10) &=6 (4 x-1) & & 9 y=18 (6)\
90 &=24 x-6 & & 9 y=108\
96 &=24 x & & y=12\\
x &=4 &
\ end {alineado}\)
Ejemplo\(\PageIndex{5}\)
Determinar si los siguientes triángulos son similares. Si es así, explique por qué y escriba la declaración de similitud.
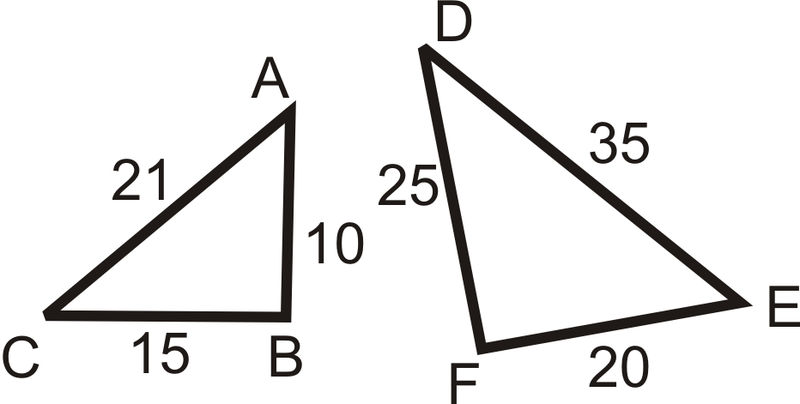
Solución
Habrá que encontrar las proporciones para los lados correspondientes de los triángulos y ver si todos son iguales. Comience con los lados más largos y trabaje hasta los lados más cortos.
\(\begin{aligned} \dfrac{AC}{ED}&=\dfrac{21}{35}=\dfrac{3}{5} \\ \dfrac{BC}{FD}&=\dfrac{15}{25}=\dfrac{3}{5} \\ \dfrac{AB}{EF}&=\dfrac{10}{20}=\dfrac{1}{2} \end{aligned}\)
Dado que las proporciones no son todas iguales, los triángulos no son similares.
Revisar
Rellene los espacios en blanco.
- Si los tres lados en un triángulo son __________________ a los tres lados en otro, entonces los dos triángulos son similares.
- Dos triángulos son similares si los lados correspondientes son _____________.
Utilice el siguiente diagrama para las preguntas 3-5. El diagrama es a escala.
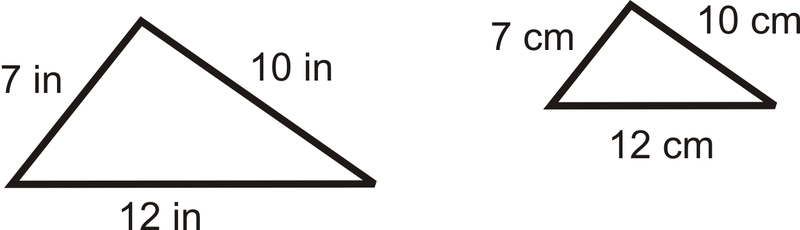
- ¿Los dos triángulos son similares? Explique su respuesta.
- ¿Los dos triángulos son congruentes? Explique su respuesta.
- ¿Cuál es el factor de escala para los dos triángulos?
Rellene los espacios en blanco en los estados de cuenta a continuación. Usa el diagrama a la izquierda.
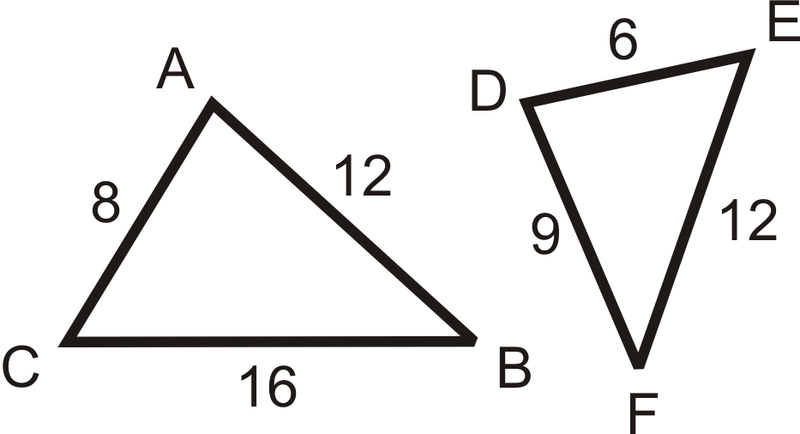
- \(\Delta ABC\sim \Delta _____\)
- \(\dfrac{AB}{?}=\dfrac{BC}{?}=\dfrac{AC}{?}\)
- Si\(\Delta ABC\) tuviera una altitud\(AG=10\), ¿cuál sería la longitud de la altitud\(\overline{DH}\)?
- Encuentra el perímetro de\(\Delta ABC\) y\(\Delta DEF\). Encuentra la relación de los perímetros.
Utilice el diagrama a la derecha para las preguntas 10-15.
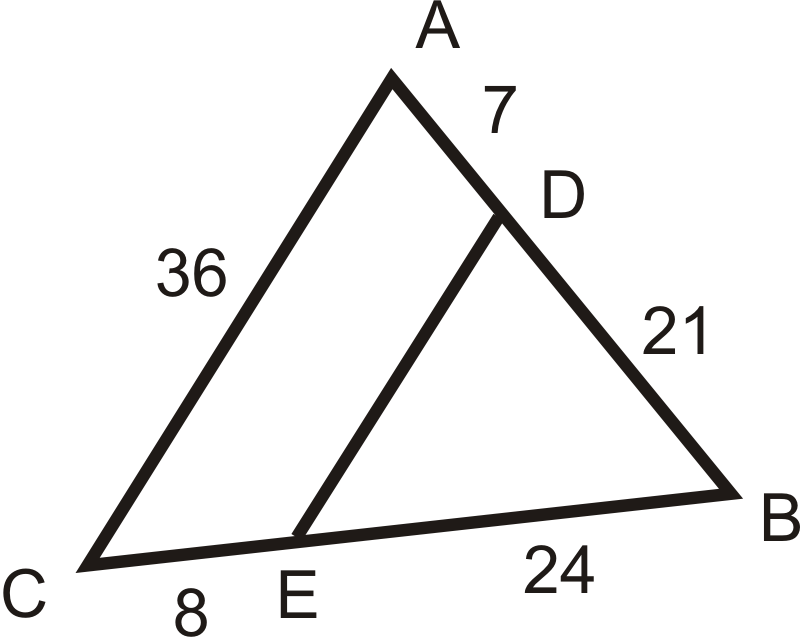Figura\(\PageIndex{8}\)- \(\Delta ABC\sim \Delta _____\)
- ¿Por qué los dos triángulos son similares?
- Encuentra\(ED\).
- \(\dfrac{BD}{?}=\dfrac{?}{BC}=\dfrac{DE}{?}\)
- ¿Es\(\dfrac{AD}{DB}=\dfrac{CE}{EB}\) verdad?
- ¿Es\(\dfrac{AD}{DB}=\dfrac{AC}{DE}\) verdad?
Encuentra el valor de la (s) variable (s) faltante (s) que hace que los dos triángulos sean similares
-
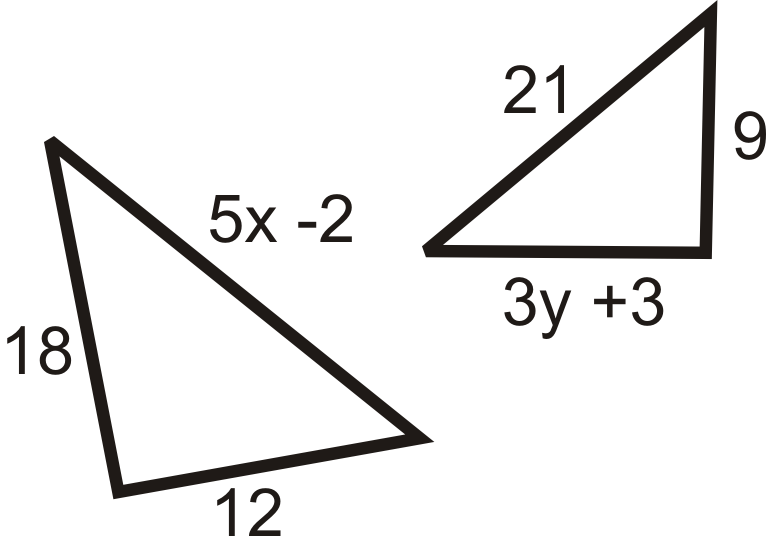
Figura\(\PageIndex{9}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.6.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Teorema de similitud AAA | El teorema de similitud AAA establece que si los tres pares de lados correspondientes de dos triángulos son proporcionales, entonces los dos triángulos son similares. |
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| Dilatación | Reducir o agrandar una figura según un factor de escala es una dilatación. |
| Ratio | Una relación es una comparación de dos cantidades que se pueden escribir en forma de fracción, con dos puntos o con la palabra “a”. |
| SSS | SSS significa lado, lado, lado y se refiere al hecho de que los tres lados de un triángulo son conocidos en un problema. |
| Transformación Rígida | Una transformación rígida es una transformación que conserva la distancia y los ángulos, no cambia el tamaño ni la forma de la figura. |
Recursos adicionales
Elemento Interactivo
Video: Triángulos Congruentes y Similares
Actividades: Preguntas de discusión sobre similitud de SSS
Ayudas de estudio: Guía de estudio de similitud poligonal
Práctica: Similitud de SSS
Mundo real: Crazy Quilt