7.12: Líneas paralelas, transversales y proporcionalidad
- Page ID
- 107442
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Como lo demuestra el Teorema de la Proporcionalidad Triangular, tres o más líneas paralelas cortadas por dos transversales las dividen proporcionalmente.
Teorema de la proporcionalidad del triángulo
El Teorema de la Proporcionalidad del Triángulo establece que si una línea paralela a un lado de un triángulo se cruza con los otros dos lados, entonces divide esos lados proporcionalmente. Podemos extender este teorema a una situación fuera de triángulos donde tenemos múltiples líneas paralelas cortadas por transversales.
Teorema: Si dos o más líneas paralelas son cortadas por dos transversales, entonces dividen las transversales proporcionalmente.
Figura\(\PageIndex{1}\)Si\(l\parallel m\parallel n\), entonces\(\dfrac{a}{b}=\dfrac{c}{d}\) o\(\dfrac{a}{c}=\dfrac{b}{d}\).
Tenga en cuenta que este teorema funciona para cualquier número de líneas paralelas con cualquier número de transversales. Cuando esto sucede, todos los segmentos correspondientes de las transversales son proporcionales.
¿Y si estuvieras viendo un mapa que mostrara cuatro calles paralelas (A, B, C y D) cortadas por dos avenidas, o transversales, (1 y 2)? ¿Cómo podrías determinar la distancia que tendrías que recorrer por la Avenida 2 para llegar a la Calle C de la Calle B dada la distancia por la Avenida 1 de la Calle A a la Calle B, la distancia por la Avenida 1 de la Calle B a la C, y la distancia por la Avenida 2 de la Calle A a la B?
Ejemplo\(\PageIndex{1}\)
Encontrar\(a\),\(b\), y\(c\).
Solución
Alinee los segmentos que están opuestos entre sí.
\ (\ begin {array} {ccc}
\ frac {a} {9} =\ frac {2} {3} &\ frac {2} {3} =\ frac {4} {b} &\ frac {2} {3} =\ frac {3} {c}\\
3 a=18 y 2 b=12 y 2 c=9\
a=6 y b=6 & c=4.5
\ end {array}\)
Ejemplo\(\PageIndex{1}\)
A continuación se muestra un mapa de calle de parte de Washington DC. La calle R, la calle Q y la calle O son paralelas y la calle 7 es perpendicular a las tres. Todas las medidas se dan en el mapa. ¿Qué son x e y?
Solución
Para encontrar x e y, es necesario establecer una proporción usando las líneas paralelas.
\(\dfrac{2640}{x}=\dfrac{1320}{2380}=\dfrac{1980}{y}\)
A partir de esto,\(x=4760\text{ ft }\) y\(y=3570\text{ ft }\).
Ejemplo\(\PageIndex{1}\)
Encuentra\(a\).
Solución
Las tres líneas están marcadas paralelas, por lo que para resolver, s et up una proporción.
\(\begin{aligned}\dfrac{a}{20}&=\dfrac{9}{15} \\ 180&=15a \\ a&=12 \end{aligned}\)
Ejemplo\(\PageIndex{1}\)
Encuentra\(b\).
Solución
Para resolver, establecer una proporción.
\(\begin{aligned} \dfrac{12}{9.6}&=\dfrac{b}{24} \\ 288&=9.6b \\ b&=30 \end{aligned}\)
Ejemplo\(\PageIndex{1}\)
Encuentra el valor de x\) que hace que las líneas sean paralelas.
Solución
Para resolver, establecer una proporción y resolver para\(x\).
\(\begin{aligned}\dfrac{5}{8}&=\dfrac{3.75}{2x−4}\rightarrow 5(2x−4)&=8(3.75) \\ 10x−20&=30 \\ 10x&=50 \\ x&=5\end{aligned}\)
Revisar
Encuentra el valor de cada variable en las imágenes a continuación.
-
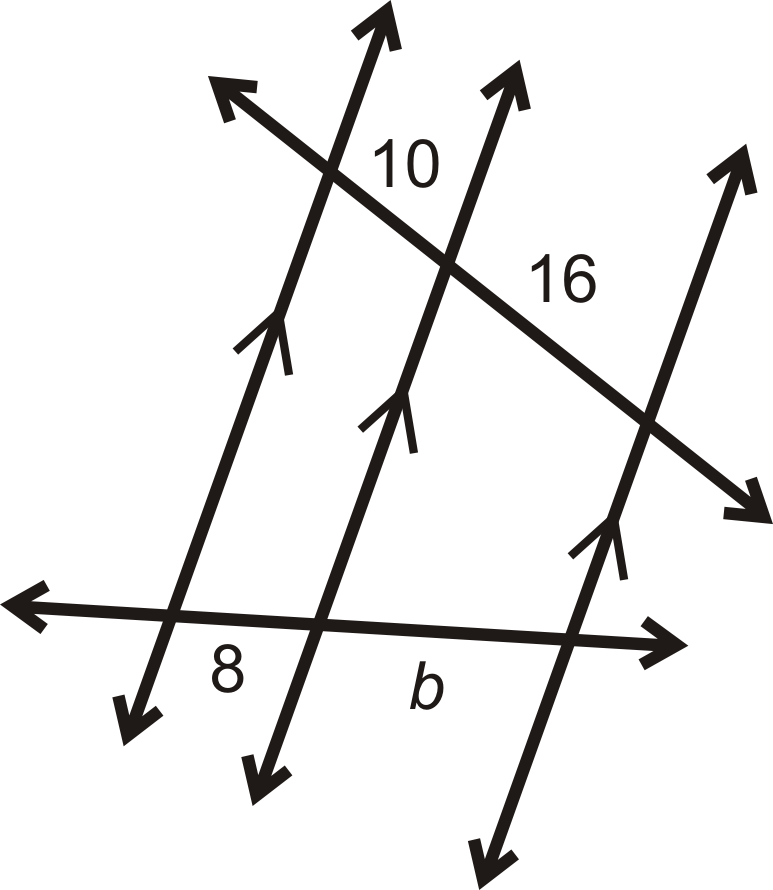
Figura\(\PageIndex{8}\) -
Figura\(\PageIndex{9}\) -
Figura\(\PageIndex{10}\) -
Figura\(\PageIndex{11}\) -
Figura\(\PageIndex{12}\)
El mapa de la calle muestra parte de Nueva Orleans. Burgundy St., Dauphine St. y Royal St. son paralelas entre sí. Si Spain St. es perpendicular a los tres, encuentra las distancias indicadas.
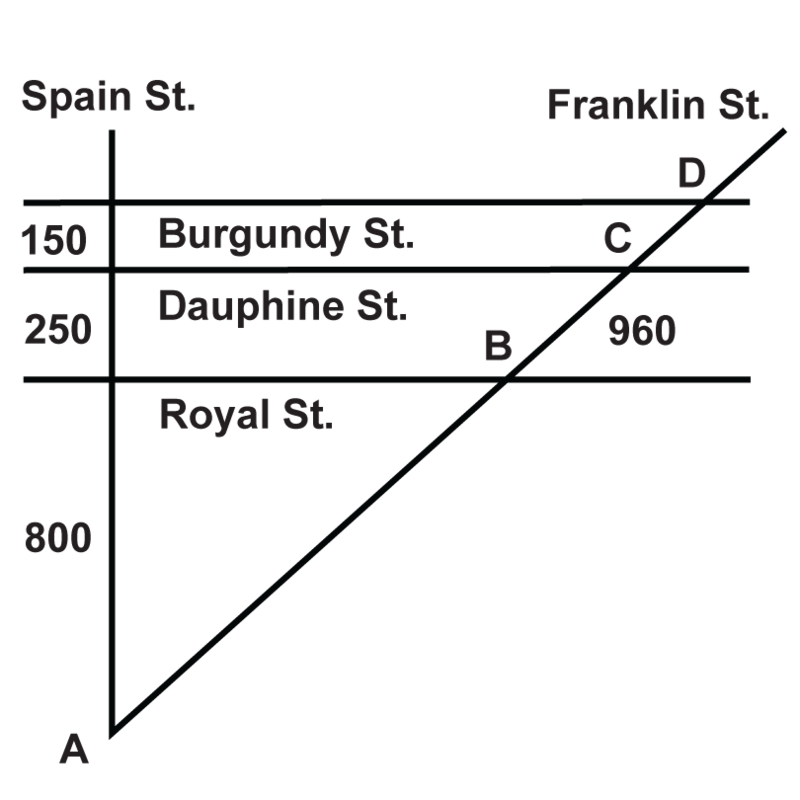
- ¿Cuál es la distancia entre puntos\(A\) y\(B\)?
- ¿Cuál es la distancia entre puntos\(C\) y\(D\)?
- ¿Cuál es la distancia entre puntos\(A\) y\(D\)?
Usando el diagrama, responde a las preguntas.
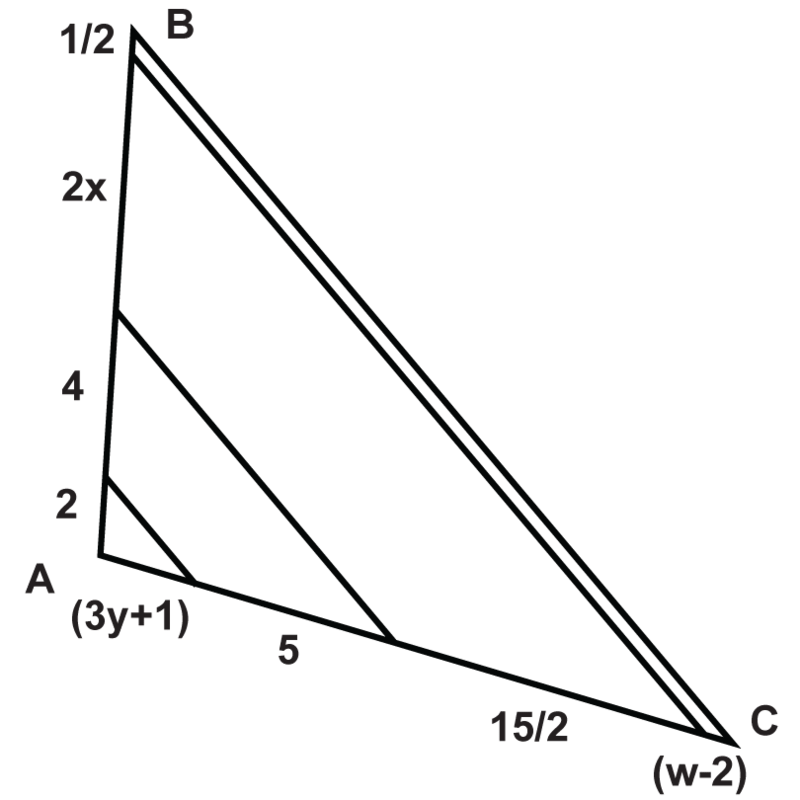
- ¿Cuál es el valor de\(w\)?
- ¿Cuál es el valor de\(x\)?
- ¿Cuál es el valor de\(y\)?
- ¿Cuál es la longitud de\(\overline{AB}\)?
- ¿Cuál es la longitud de\(\overline{AC}\)?
Usando el diagrama, rellene el espacio en blanco.
- Si\(b\) es un tercio\(d\), entonces\(a\) es ____________________.
- Si\(c\) es dos veces\(a\), entonces\(b\) es ____________________.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.9.
El vocabulario
| Término | Definición |
|---|---|
| Plano de coordenadas | El plano de coordenadas es una rejilla formada por una recta numérica horizontal y una recta numérica vertical que se cruzan en el punto (0, 0), denominado origen. El plano de coordenadas también se llama Plano Cartesiano. |
| perpendiculares | Las líneas perpendiculares son líneas que se cruzan en un ángulo de 90°. El producto de las pendientes de dos líneas perpendiculares es -1. |
| Proporción | Una proporción es una ecuación que muestra dos proporciones equivalentes. |
| Cuadrilátero | Un cuadrilátero es una figura cerrada con cuatro lados y cuatro vértices. |
| transversal | Una transversal es una línea que cruza otras dos líneas. |
| Teorema de la proporcionalidad del triángulo | El Teorema de la Proporcionalidad del Triángulo establece que si una línea es paralela a un lado de un triángulo y se cruza con los otros dos lados, entonces divide esos lados proporcionalmente. |
Recursos adicionales
Elemento interactivo
Video: Ejemplos de Líneas Paralelas y Transversales - Básico
Actividades: Líneas Paralelas y Transversales Preguntas de Discusión
Ayudas de estudio: Guía de estudio de relaciones de proporcionalidad
Práctica: Líneas paralelas, transversales y proporcionalidad
Mundo Real: Líneas Paralelas y Transversales