7.11: Triángulos Similares Inscritos
- Page ID
- 107427
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)División de un triángulo rectángulo en triángulos similares usando una altitud.
Teorema de Triángulos Similares Inscritos
Recuerda que si dos objetos son similares, sus ángulos correspondientes son congruentes y sus lados son proporcionales en longitud. La altitud de un triángulo rectángulo crea triángulos similares.
Teorema de triángulos similares inscritos: Si se dibuja una altitud desde el ángulo recto de cualquier triángulo rectángulo, entonces los dos triángulos formados son similares al triángulo original y los tres triángulos son similares entre sí.
En\(\Delta ADB\),\(m\angle A=90^{\circ}\) y\(\overline{AC}\perp \overline{DB}\):

Entonces,\(\Delta ADB\sim \Delta CDA\sim \Delta CAB\):

Esto significa que todos los lados correspondientes son proporcionales. Puedes usar este dato para encontrar longitudes faltantes en triángulos rectos.
¿Y si trazas una línea desde el ángulo recto de un triángulo rectángulo perpendicular al lado opuesto a ese ángulo? ¿Cómo podrías determinar la longitud de esa línea?
Ejemplo\(\PageIndex{1}\)
Encuentra el valor de\(x\).

Solución
Establecer una proporción.
\(\begin{aligned} \dfrac{\text{ shorter leg in }\Delta SVT}{\text{ shorter leg in }\Delta RST}&=\dfrac{\text{ hypotenuse in }\Delta SVT}{ \text{ hypotenuse in }\Delta RST} \\ \dfrac{4}{x}&=\dfrac{x}{20} \\ x^2&=80 \\ x&=\sqrt{80}=4\sqrt{5} \end{aligned}\)
Ejemplo\(\PageIndex{2}\)
Ahora encuentra el valor de\(y\) en\(\Delta RST\) arriba.
Solución
Usa el Teorema de Pitágoras.
\(\begin{aligned} y^2+(4\sqrt{5})^2&=20^2 \\y^2+80&=400 \\ y^2&=320 \\ y&=\sqrt{320}=8\sqrt{5}\end{aligned}\)
Ejemplo\(\PageIndex{3}\)
Encuentra el valor de\(x\).

Solución
Separar los triángulos para encontrar los lados correspondientes.

Establecer una proporción.
\(\begin{aligned} \dfrac{\text{ shorter leg in } \Delta EDG}{\text{ shorter leg in } \Delta DFG}&=\dfrac{\text{ hypotenuse in }\Delta EDG}{\text{ hypotenuse in }\Delta DFG} \\ \dfrac{6}{x}&=\dfrac{10}{8} \\ 48&=10x \\ 4.8&=x \end{aligned}\)
Ejemplo\(\PageIndex{4}\)
Encuentra el valor de\(x\).
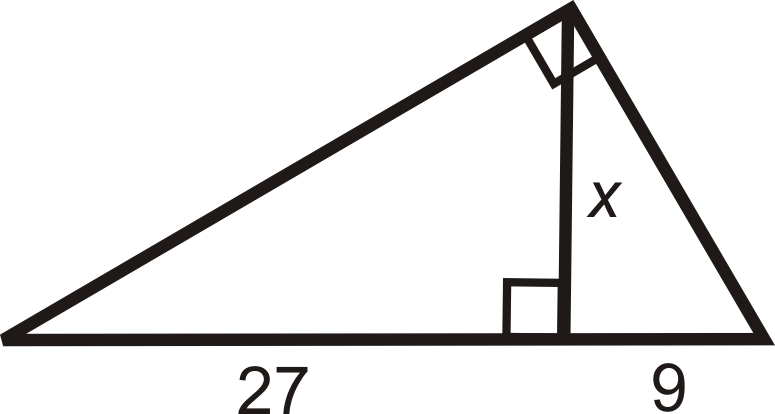
Solución
Establecer una proporción.
\(\begin{aligned}\dfrac{\text{ shorter leg of smallest }\Delta}{\text{ shorter leg of middle } \Delta}=\dfrac{ \text{ longer leg of smallest }\Delta }{\text{ longer leg of middle }\Delta} \\ \dfrac{9}{x}&=\dfrac{x}{27} \\ x^2&=243 \\ x&=\sqrt{243}=9\sqrt{3}\end{aligned}\)
Ejemplo\(\PageIndex{5}\)
Encuentra los valores de\(x\) y\(y\).

Separar los triángulos. Escribe una proporción para\(x\).
Solución

\(\begin{aligned} \dfrac{20}{x}&=\dfrac{x}{35} \\ x^2&=20\cdot 35 \\ x&=\sqrt{20\cdot 35} \\ x&=10\sqrt{7}\end{aligned}\)
Establecer una proporción para y. O, ahora que conoces el valor de x\) puedes usar el Teorema de Pitágoras para resolver para\(y\). Usa el método con el que te sientas más cómodo.
\ (\ begin {array} {rlrl}
\ frac {15} {y} & =\ frac {y} {35} & (10\ sqrt {7}) ^ {2} +y^ {2} & =35^ {2}\
y^ {2} & =15\ cdot 35 & 700+y^ {2} &=1225\\
y & =\ sqrt 15\ cdot 35} & y&=\ sqrt {525} =5\ sqrt {21}\\ & &
y &=5\ sqrt {21}
\ end {array}\)
Revisar
Rellene los espacios en blanco.

- \(\Delta BAD\sim \Delta ______ \sim \Delta ______\)
- \(\dfrac{BC}{?}=\dfrac{?}{CD}\)
- \(\dfrac{BC}{AB}=\dfrac{AB}{?}\)
- \(\dfrac{?}{AD}=\dfrac{AD}{BD}\)
Escribe la declaración de similitud para los triángulos rectos en cada diagrama.
-

Figura\(\PageIndex{10}\) -

Figura\(\PageIndex{11}\)
Utilice el diagrama para responder a las preguntas 7-10.

- Escribe la declaración de similitud para los tres triángulos en el diagrama.
- Si\(JM=12\) y\(ML=9\), encuentra\(KM\).
- Encuentra\(JK\).
- Encuentra\(KL\).
Encuentra la longitud de la (s) variable (s) faltante (s) Simplifica todos los radicales.
-

Figura\(\PageIndex{13}\) -

Figura\(\PageIndex{14}\) -
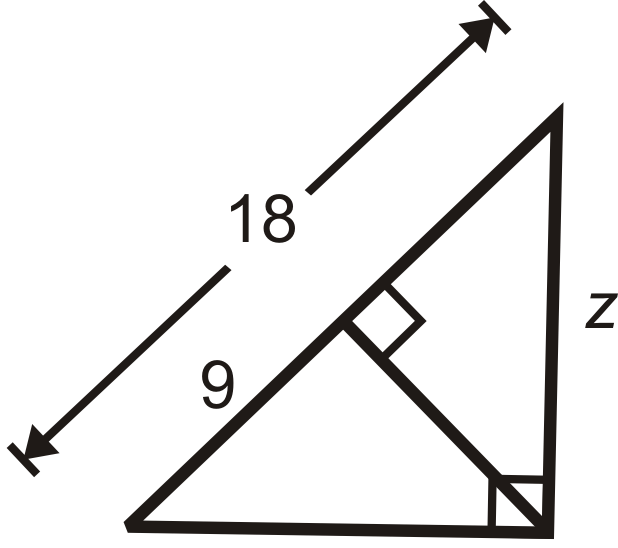
Figura\(\PageIndex{15}\) -
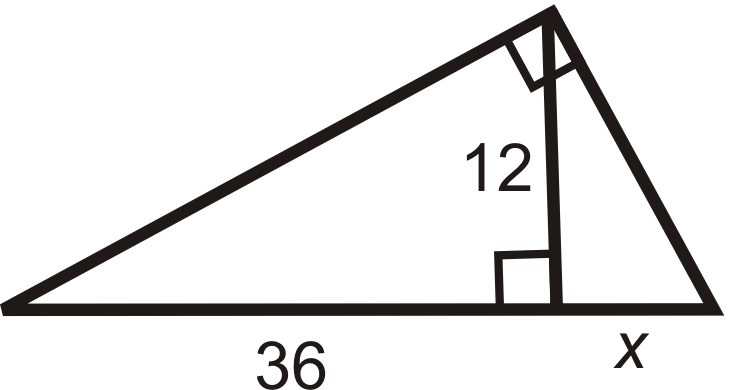
Figura\(\PageIndex{16}\) -

Figura\(\PageIndex{17}\) -
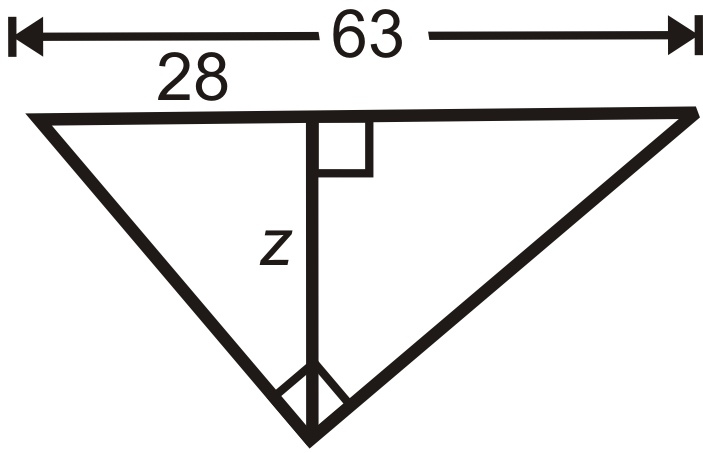
Figura\(\PageIndex{18}\) -

Figura\(\PageIndex{19}\) -
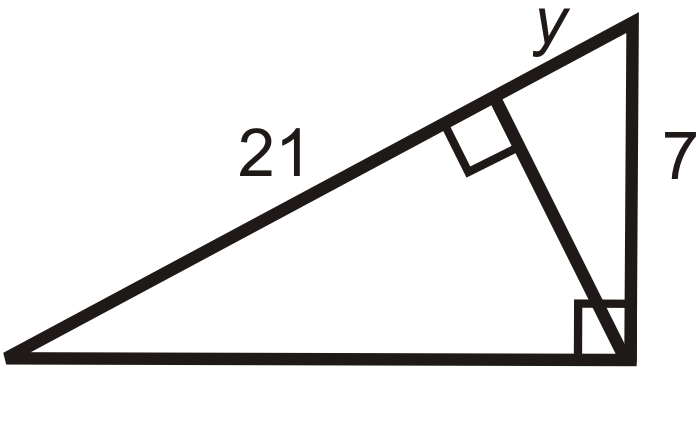
Figura\(\PageIndex{20}\) -

Figura\(\PageIndex{21}\) -

Figura\(\PageIndex{22}\) -

Figura\(\PageIndex{23}\) -
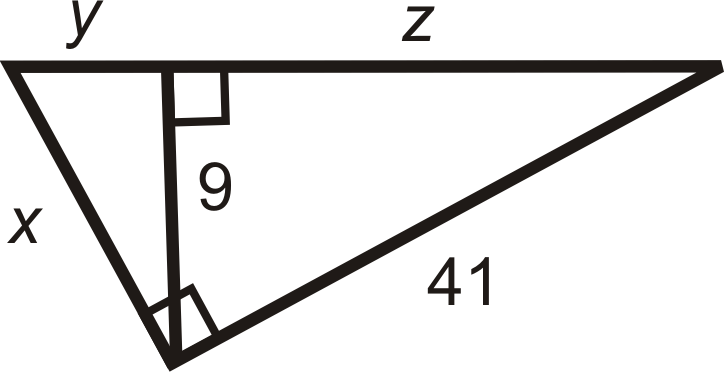
Figura\(\PageIndex{24}\) - Rellene los espacios en blanco de la prueba para el Teorema de Triángulos Similares Inscritos.

Figura\(\PageIndex{25}\)
Dado:\(\Delta ABD\) con\(\overline{AC}\perp \overline{DB}\) y\(\angle DAB\) es un ángulo recto.
Demostrar:\(\Delta ABD\sim \Delta CBA\sim \Delta CAD\)
| Comunicado | Razón |
|---|---|
| 1. | 1. Dado |
| 2. \(\angle DCA\)y\(\angle ACB\) son ángulos rectos | 2. |
| 3. \(\angle DAB\cong \angle DCA\cong \angle ACB\) | 3. |
| 4. | 4. PoC reflexivo |
| 5. | 5. Postulado de similitud AA |
| 6. \(B\cong \angle B\) | 6. |
| 7. \(\Delta CBA\cong \Delta ABD\) | 7. |
| 8. \(\Delta CAD\cong \Delta CBA\) | 8. |
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.4.
El vocabulario
| Término | Definición |
|---|---|
| Teorema de Triángulos Similares | El Teorema de Triángulos Similares Inscritos establece que si se dibuja una altitud desde el ángulo recto de cualquier triángulo rectángulo, entonces los dos triángulos formados son similares al triángulo original y los tres triángulos son similares entre sí. |
| perpendiculares | Las líneas perpendiculares son líneas que se cruzan en un ángulo de 90°. El producto de las pendientes de dos líneas perpendiculares es -1. |
| Proporción | Una proporción es una ecuación que muestra dos proporciones equivalentes. |
| Teorema de Pitágoras | El Teorema de Pitágoras es una relación matemática entre los lados de un triángulo rectángulo\(a^2+b^2=c^2\), dada por, donde a y b son patas del triángulo y c es la hipotenusa del triángulo. |
Recursos adicionales
Video: Principios de Triángulos Similares Inscritos - Básico
Actividades: Triángulos Similares Inscritos Preguntas de Discusión
Ayudas de estudio: Guía de estudio de similitud de triángulo rectángulo
Práctica: Triángulos Similares Inscritos
Mundo Real: Triángulos Similares Inscritos

