7.17: Mapeo de dilataciones
- Page ID
- 107462
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Figuras que se pueden llevar entre sí utilizando una o más transformaciones rígidas seguidas de una dilatación. Reglas que describen los cambios de tamaño dados de las imágenes
Reglas para dilataciones
La siguiente figura muestra una dilatación de dos trapecios. Escribe la regla de mapeo para la dilatación de la Imagen A a la Imagen B.
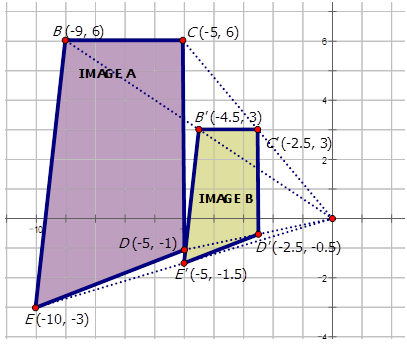
En geometría, una transformación es una operación que mueve, voltea o cambia una forma para crear una nueva forma. Una dilatación es un tipo de transformación que agranda o reduce una figura (llamada preimagen) para crear una nueva figura (llamada imagen). El factor de escala\(r\),, determina cuánto mayor o menor será la imagen de dilatación comparada con la preimagen.
Mira el diagrama a continuación:
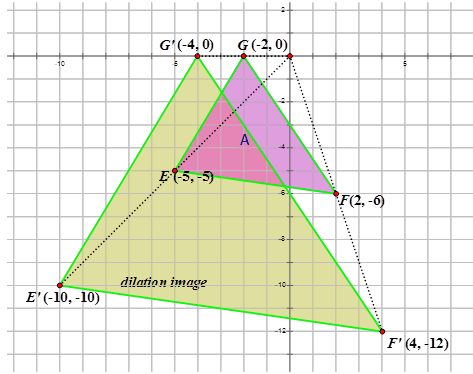
La Imagen A ha sufrido una dilatación sobre el origen con un factor de escala de 2. Observe que los puntos en la imagen de dilatación son todos el doble de los puntos de coordenadas en la preimagen. Una dilatación con un factor de escala\(k\) sobre el origen se puede describir utilizando la siguiente notación:
\(D_{k} (x,y)=(kx,ky)\)
\(k\)siempre será un valor que sea mayor que 0.
| Factor de Escala, k | Cambio de tamaño para preimagen |
|---|---|
| \(k>1\) | La imagen de dilatación es más grande que la preimagen |
| \(0<k<1\) | La imagen de dilatación es más pequeña que la preimagen |
| \(k=1\) |
La imagen de dilatación es del mismo tamaño que la preimagen |
Dibujemos la imagen de dilatación para las siguientes asignaciones:
- La regla de mapeo para la dilatación aplicada al triángulo de abajo es\((x,y)\rightarrow (1.5x,1.5y)\).
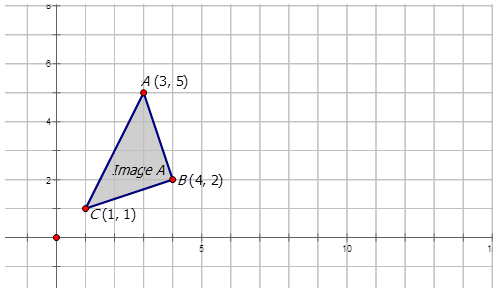
Con un factor de escala de 1.5, cada punto de coordenada se multiplicará por 1.5.
\ (\ begin {array} {llcc}
\ text {Imagen} A y A (3,5) y B (4,2) & C (1,1)\\
\ texto {Imagen de dilatación} & A^ {\ prime} (4.5,7.5) & B^ {\ prime} (6,3) & C^ {\ prime} (1.5,1.5)
\ end {array}\)
La imagen de dilatación tiene el siguiente aspecto:
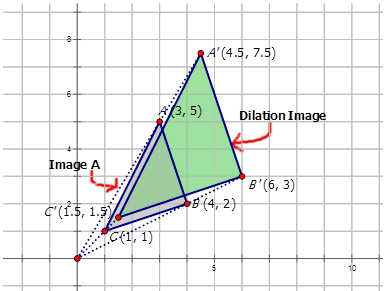
- La regla de mapeo para la dilatación aplicada al diagrama a continuación es\((x,y)\rightarrow (\dfrac{1}{3}x, \dfrac{1}{3}y)\).
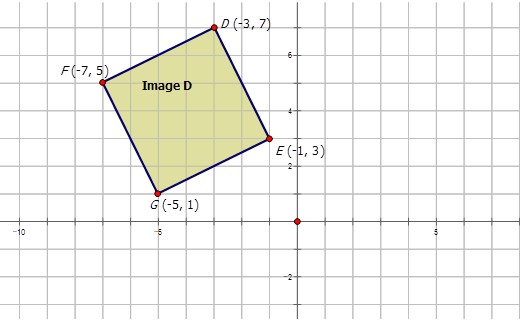
Con un factor de escala de\(\dfrac{1}{3}\), cada punto de coordenada se multiplicará por\(\dfrac{1}{3}\).
\ (\ begin {array} {llllr}
\ text {Imagen} D & D (-3,7) & E (-1,3) & F (-7,5) & G (-5,1)\\
\ text {Imagen de dilatación} & D^ {\ prime} (-1,2.3) y E^ {\ prime} (-0.3,1) y F^ {\ prime} (-2.3,1.7) y G^ {\ prime} prime} (-1.7,0.3)
\ end {array}\)
La imagen de dilatación tiene el siguiente aspecto:
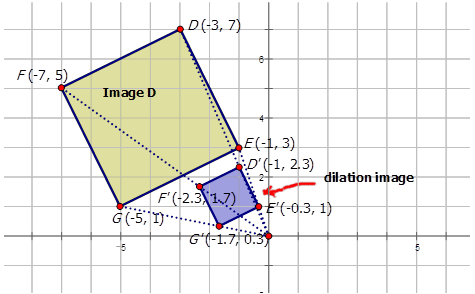
Ahora, escribamos la notación que representa la dilatación de la preimagen A a la imagen de dilatación J en el siguiente diagrama:
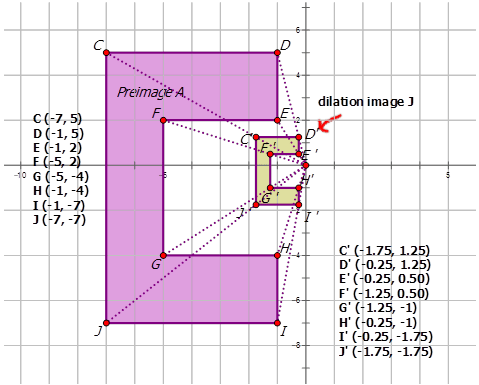
Primero, elige un punto en el diagrama para usar para ver cómo se ha visto afectado por la dilatación.
\(C:(−7,5)\qquad C′:(−1.75,1.25)\)
Observe cómo las coordenadas x e y se multiplican por\(\dfrac{1}{4}\). Esto indica que la preimagen\(A\) sufre una dilatación sobre el origen por un factor de escala de\(\dfrac{1}{4}\) para formar la imagen de dilatación\(J\). Por lo tanto la notación de mapeo es\((x,y)\rightarrow (\dfrac{1}{4}x,\dfrac{1}{4}y)\).
Ejemplo\(\PageIndex{1}\)
Anteriormente, se le pidió que escribiera la regla de mapeo para la dilatación de la Imagen A a la Imagen B en la imagen de abajo:

Solución
Mira los puntos en cada imagen:
\ (\ begin {array} {lllll}
\ texto {Imagen} A y B (-9,6) y C (-5,6) y D (-5, -1) & E (-10, -3)\
\ texto {Imagen} B & B^ {\ prime} (-4.5,3) y C^ {\ prime} (-2.5,3) y D^ {\ prime} (-2.5, -0.5) & E^ {\ prime} (-5, -1.5)
\ end {array}\)
Observe que los puntos de coordenadas en la Imagen B (la imagen de dilatación) son\ dfrac {1} {2}\) que se encuentran en la Imagen A\). Por lo tanto, la Imagen A sufre una dilatación sobre el origen del factor de escala\ dfrac {1} {2}\). Para escribir una regla de mapeo para esta dilatación escribirías: (x, y)\ rightarrow (\ dfrac {1} {2} x,\ dfrac {1} {2} y)\).
Ejemplo\(\PageIndex{2}\)
Thomas describe una dilatación de punto\(JT\) con vértices\(J(−2,6)\)\(T(6,2)\) a punto\(J′T′\) con vértices\(J′(−4,12)\) y\(T′(12,4)\). Escribe la notación para describir esta dilatación para Thomas.
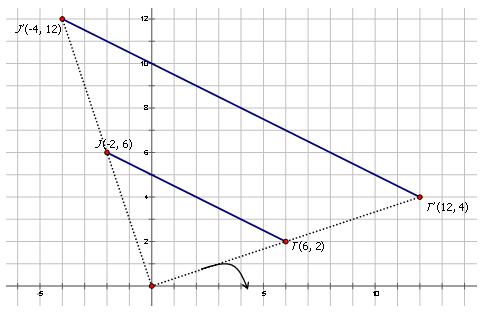
Solución
Dado que las coordenadas x e y se multiplican cada una por 2, el factor de escala es 2. La notación de mapeo es:\((x,y)\rightarrow (2x,2y)\)
Ejemplo\(\PageIndex{3}\)
Dados los puntos\(A(12,8)\) y\(B(8,4)\) en una línea experimentando una dilatación para producir\(A′(6,4)\) y\(B′(4,2)\), escribir la notación que representa la dilatación.
Solución
Para escribir la notación para describir la dilatación, elija un punto en la preimagen y luego el punto correspondiente en la imagen de dilatación para ver cómo se ha movido el punto. Observe que el punto EA\) es:
\(A(12,8)\rightarrow A′(6,4)\)
Dado que ambas coordenadas x e y se multiplican por\(\dfrac{1}{2}\), la dilatación es sobre el origen tiene un factor de escala de\(\dfrac{1}{2}\). La notación para esta dilatación sería:\((x,y)\rightarrow (\dfrac{1}{2}x,\dfrac{1}{2}y)\).
Ejemplo\(\PageIndex{4}\)
Janet estaba jugando con un programa de dibujo en su computadora. Ella creó los siguientes diagramas y luego quiso determinar las transformaciones. Escribe la regla de notación que representa la transformación del diagrama púrpura y azul al diagrama naranja y azul.
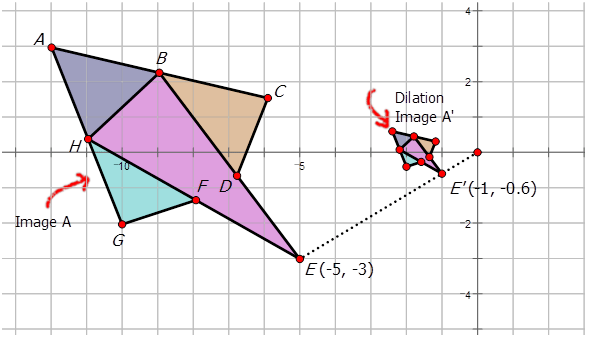
Solución
Para escribir la notación para describir la dilatación, elija un punto en la preimagen\(A\) y luego el punto correspondiente en la imagen de dilatación\(A′\) para ver cómo ha cambiado el punto. Observe que el punto\(E\) se muestra en el diagrama:
\(E(−5,−3)\rightarrow E′(−1,−0.6)\)
Dado que ambas coordenadas x e y se multiplican por\(\dfrac{1}{5}\), la dilatación es sobre el origen tiene un factor de escala de\(\dfrac{1}{5}\). La notación para esta dilatación sería:\((x,y)\rightarrow (\dfrac{1}{5}x, \dfrac{1}{5}y)\).
Revisar
Complete la siguiente tabla. Supongamos que el centro de dilatación es el origen.
| Punto de partida | \(D_{2}\) | \(D_{5}\) | \(D_{\dfrac{1}{2}}\) | \(D_{\dfrac{3}{4}}\) |
|---|---|---|---|---|
| 1. (1, 4) | \ (D_ {2}\)” class="lt-k12-5951"> | \ (D_ {5}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)” class="lt-k12-5951"> |
| 2. (4, 2) | \ (D_ {2}\)” class="lt-k12-5951"> | \ (D_ {5}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)” class="lt-k12-5951"> |
| 3. (2, 0) | \ (D_ {2}\)” class="lt-k12-5951"> | \ (D_ {5}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)” class="lt-k12-5951"> |
| 4. (-1, 2) | \ (D_ {2}\)” class="lt-k12-5951"> | \ (D_ {5}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)” class="lt-k12-5951"> |
| 5. (-2, -3) | \ (D_ {2}\)” class="lt-k12-5951"> | \ (D_ {5}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)” class="lt-k12-5951"> |
| 6. (9, 4) | \ (D_ {2}\)” class="lt-k12-5951"> | \ (D_ {5}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)” class="lt-k12-5951"> |
| 7. (-1, 3) | \ (D_ {2}\)” class="lt-k12-5951"> | \ (D_ {5}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)” class="lt-k12-5951"> |
| 8. (-5, 2) | \ (D_ {2}\)” class="lt-k12-5951"> | \ (D_ {5}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)” class="lt-k12-5951"> |
| 9. (2, 6) | \ (D_ {2}\)” class="lt-k12-5951"> | \ (D_ {5}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)” class="lt-k12-5951"> |
| 10. (-5, 7) | \ (D_ {2}\)” class="lt-k12-5951"> | \ (D_ {5}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {1} {2}}\)” class="lt-k12-5951"> | \ (D_ {\ dfrac {3} {4}}\)” class="lt-k12-5951"> |
Escribe la notación que representa la dilatación de la preimagen a la imagen para cada diagrama a continuación.
-
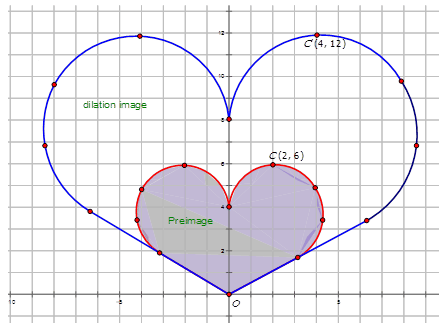
Figura\(\PageIndex{11}\) -
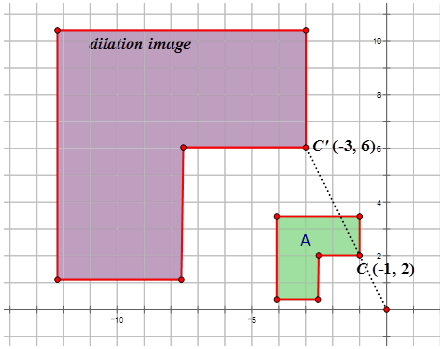
Figura\(\PageIndex{12}\) -
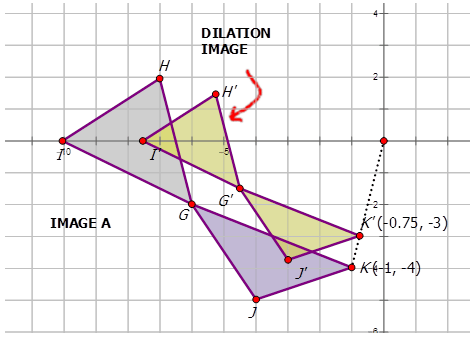
Figura\(\PageIndex{13}\) -
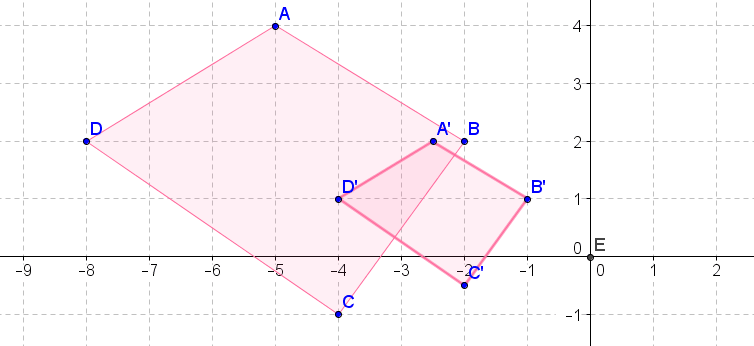
Figura\(\PageIndex{14}\) -
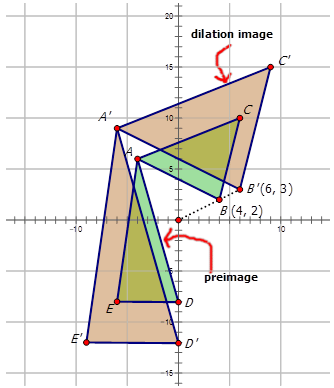
Figura\(\PageIndex{15}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.12.
Recursos adicionales
Elemento interactivo
Video: SAT Math (Geometría) - Práctica 2.7
Práctica: Mapeo de dilataciones

