8.2: Líneas de simetría
- Page ID
- 107591
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identificar existencia y número de líneas de simetría.
Identificar líneas de simetría
La simetría es la clave para el equilibrio de un diseño o estructura.
¿Qué es la simetría? ¿Cómo tiene simetría una imagen? ¿Qué tendría que hacer para estar seguro de que una imagen o construcción era simétrica?
En este concepto, aprenderás a identificar líneas de simetría.
Simetría
En ocasiones, una figura tendrá partes que se reflejan dentro de un objeto. En este caso, partes del objeto coinciden con otras partes de la imagen. Esto se llama simetría.
Veamos un ejemplo.
Mira este corazón. Tiene dos lados que coinciden. El corazón es simétrico porque hay simetría en su diseño. Este corazón se puede dividir por la mitad verticalmente donde una mitad coincide con la otra mitad.
Esta línea que divide el corazón en partes coincidentes se llama la línea de simetría.
Se pueden determinar otras líneas de simetría mirando otros objetos.
Veamos otro ejemplo.
Mira esta cruz. Tiene dos líneas de simetría. Si miras, la cruz se puede dividir por la mitad perfectamente verticalmente y por la mitad horizontalmente.
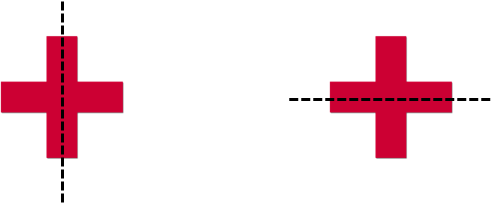
Esto quiere decir que hay dos líneas de simetría en la cruz.
Ejemplo\(\PageIndex{1}\)
Anteriormente, se le dio un problema sobre preguntas sobre simetría.
- ¿Qué es la simetría?
- ¿Cómo tiene simetría una imagen?
- ¿Qué tendrías que hacer para estar seguro de que tu imagen es simétrica?
Solución
- La simetría es cuando dos mitades de un objeto coinciden. En otras palabras, se puede dividir el objeto en partes y las partes son congruentes. Un corazón es un objeto simétrico, así es la letra A.
- Una imagen tiene simetría porque se puede dividir por la mitad para que una mitad de la imagen coincida con la otra mitad.
- Para que una imagen tenga una línea de simetría la imagen debe poder plegar sola la línea de simetría para que las dos partes sean imágenes especular entre sí. La línea plegada sería la línea de simetría. Una imagen simétrica tendría una línea de simetría como un cuadrado (cuatro líneas de simetría), un círculo (líneas infinitas de simetría) o una mariposa (una línea de simetría).
Ejemplo\(\PageIndex{2}\)
¿Esta figura tiene simetría? ¿Puede ser un reflejo?
Solución
Primero, trata de dividir esta mariposa de manera uniforme para que un lado pueda reflejar el otro. ¿Se puede trazar una línea de simetría?
La respuesta es sí.
Por lo tanto, tiene simetría.
Ejemplo\(\PageIndex{3}\)
¿La siguiente figura tiene simetría? ¿Puede ser un reflejo?
Solución
Primero, trata de dividir esta flor de manera uniforme para que un lado pueda reflejar el otro. ¿Se puede trazar una línea de simetría?
La respuesta es sí.
Por lo tanto, tiene simetría.
Ejemplo\(\PageIndex{4}\)
¿Cuántas líneas de simetría tiene esta figura?
Solución
Primero, trata de dividir este rectángulo de manera uniforme para que un lado pueda reflejar el otro. ¿Se puede trazar una línea de simetría?
La respuesta es sí. Por lo tanto, un rectángulo tiene dos líneas de simetría.
Ejemplo\(\PageIndex{5}\)
¿Estas figuras tienen simetría?
Solución
Primero, trata de dividir estas imágenes de manera uniforme para que un lado pueda reflejar el otro. ¿Se puede trazar una línea de simetría para alguna de estas imágenes?
La respuesta es no.
Por lo tanto, ninguna de estas imágenes tiene una línea de simetría.
Revisar
Usa la ilustración para responder a cada pregunta.
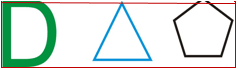
1. ¿Estas figuras tienen simetría?
2. ¿Pueden ser reflexiones?
3. ¿Cuántas líneas de simetría tiene cada figura?
Encuentra todas las líneas de simetría para las formas a continuación.
-
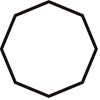
Figura\(\PageIndex{14}\) -
Figura\(\PageIndex{15}\) -
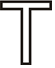
Figura\(\PageIndex{16}\)
Nombra el número de líneas de simetría para cada letra.
-
Figura\(\PageIndex{17}\) -
Figura\(\PageIndex{18}\) -
Figura\(\PageIndex{19}\) -
Figura\(\PageIndex{20}\) -
Figura\(\PageIndex{21}\)
Responder a cada pregunta verdadera o falsa.
12. Todos los triángulos tienen simetría.
13. Todos los círculos tienen simetría.
14. La letra “\(x\)” tiene dos líneas de simetría.
15. La letra “\(s\)” tiene dos líneas de simetría.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.13.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Líneas de simetría | Las líneas de simetría son las líneas que se pueden dibujar para dividir una figura en mitades iguales. |
| Reflexión | Una reflexión es una transformación que voltea una figura en el plano de coordenadas a través de una línea dada sin cambiar la forma o el tamaño de la figura. |
| Simetría | Una figura tiene simetría si se puede transformar y seguir pareciendo igual. |
Recursos adicionales
Video: Tutorial de simetría rotacional
Práctica: Líneas de simetría
Mundo real: El equilibrio de la naturaleza