8.16: Reflejando cifras
- Page ID
- 107574
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Mueva figuras en el plano de coordenadas usando patrones.
Traducciones, Rotaciones y Reflexiones
Tyler toma una foto de un artículo y su reflejo. Coloca un plano de coordenadas sobre la imagen. El plano de coordenadas se posiciona de manera que el\(x\) eje −separa la imagen de la reflexión. Luego hace la cuadrícula de acuerdo a las características clave de la imagen, de manera que un punto at\((2, 0)\) se refleja en el punto\((-2, 0)\). Si las coordenadas originales de la imagen son\((3, 0)\),\((4, 6)\) y\((5, 1)\), ¿cuáles son las coordenadas del reflejo?

En este concepto, aprenderás a encontrar las coordenadas para traducciones, rotaciones y reflexiones.
Búsqueda de coordenadas para traducciones, rotaciones y reflexiones
Cuando realizas traducciones, deslizas una figura hacia la izquierda o hacia la derecha, hacia arriba o hacia abajo. Esto significa que en el plano de coordenadas, las coordenadas para los vértices de la figura cambiarán.
Para graficar una traducción, realice el mismo cambio para cada punto.
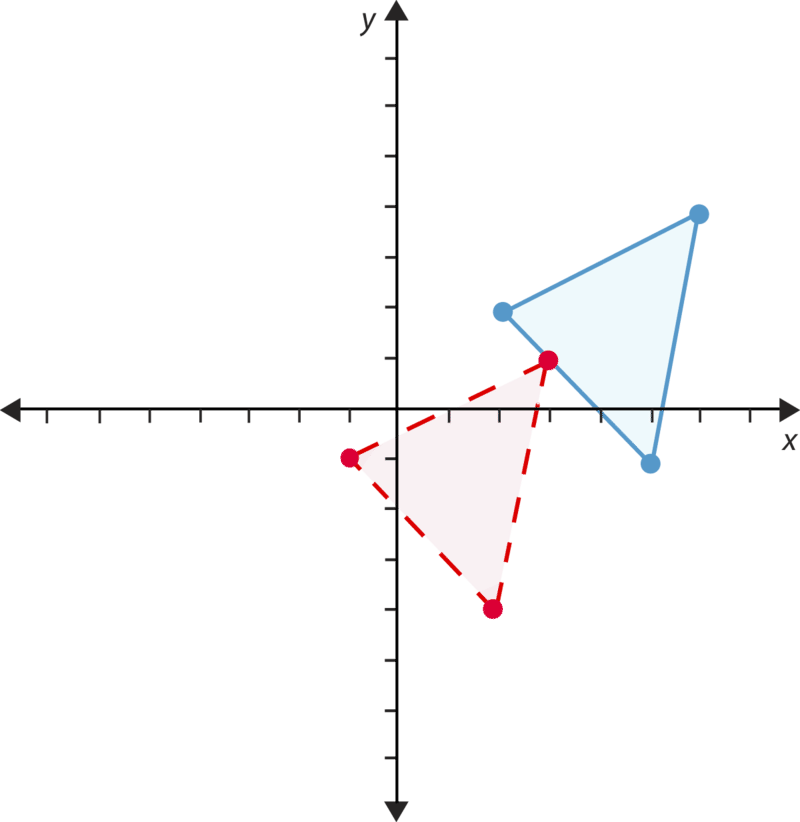
Se puede identificar un reflejo por los cambios en sus coordenadas. En una reflexión , la figura se voltea a través de una línea para hacer una imagen especular de sí misma. Echa un vistazo a la reflexión a continuación.
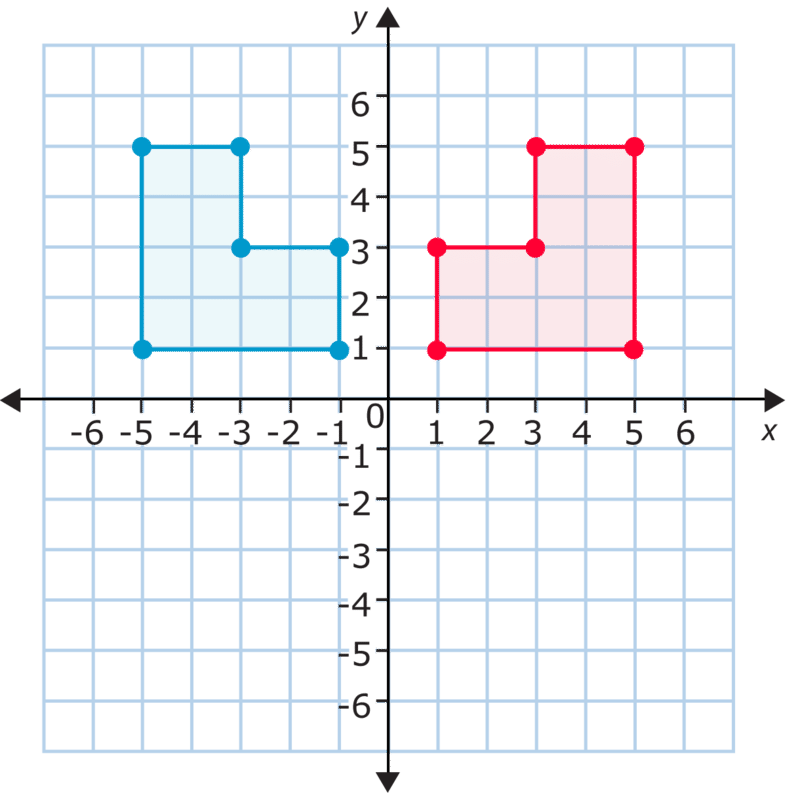
Las cifras generalmente se reflejan a través del\(x\) eje - o el\(y\) eje. En este caso, la figura se refleja a través del\(y\) eje. Si comparas las figuras del primer ejemplo vértice por vértice, verás que las\(x\) coordenadas −cambian pero las\(y\) coordenadas −permanecen iguales. Esto se debe a que la reflexión ocurre de izquierda a derecha a través del\(y\) eje. Cuando reflexiona a través del\(x\) eje\(y\) −, las coordenadas −cambian y las\(x\) coordenadas −permanecen iguales. Echa un vistazo a este ejemplo.
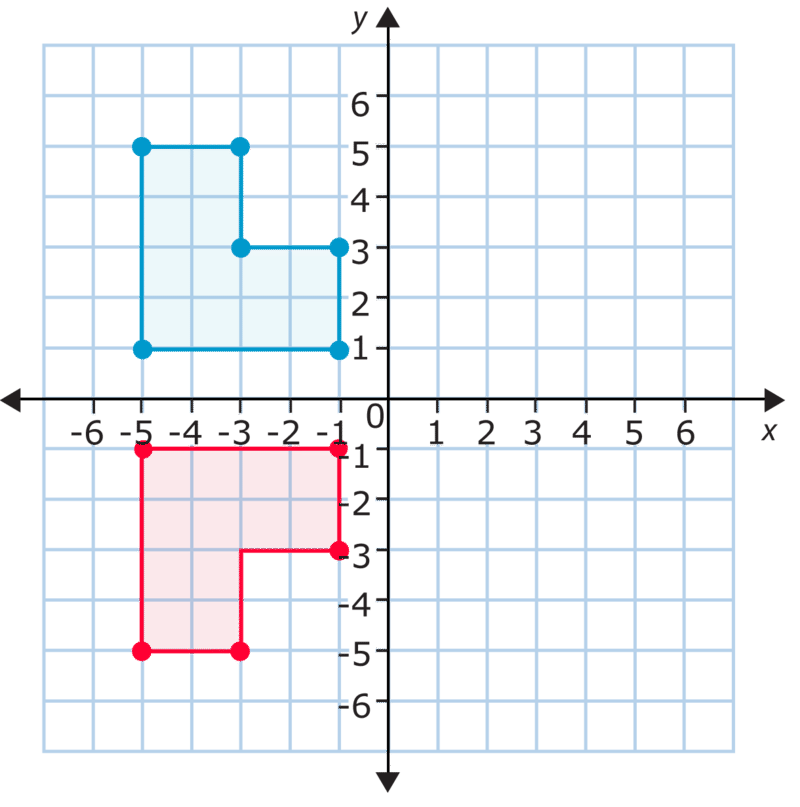
En la figura anterior se encuentran las coordenadas para el vértice superior izquierdo de la figura original\((-5, 5)\). Después de reflejarlo a través del\(x\) eje −, las coordenadas para el vértice correspondiente son\((-5, -5)\). ¿Qué tal el vértice inferior derecho? Comienza a las\((-1, 1)\), y después de la vuelta está en\((-1, -1)\). Como puede ver, las\(x\) coordenadas −permanecen iguales mientras cambian las\(y\) coordenadas −. De hecho, todas las\(y\) coordenadas −se convierten en los enteros opuestos de las\(y\) coordenadas −originales. Esto indica que se trata de una reflexión vertical (arriba/abajo) o una reflexión sobre el\(x\) eje −axis.
En una reflexión horizontal (izquierda/derecha) o una reflexión sobre el\(y\) eje, las\(x\) coordenadas −se convertirían en opuestos enteros. Veamos un ejemplo.
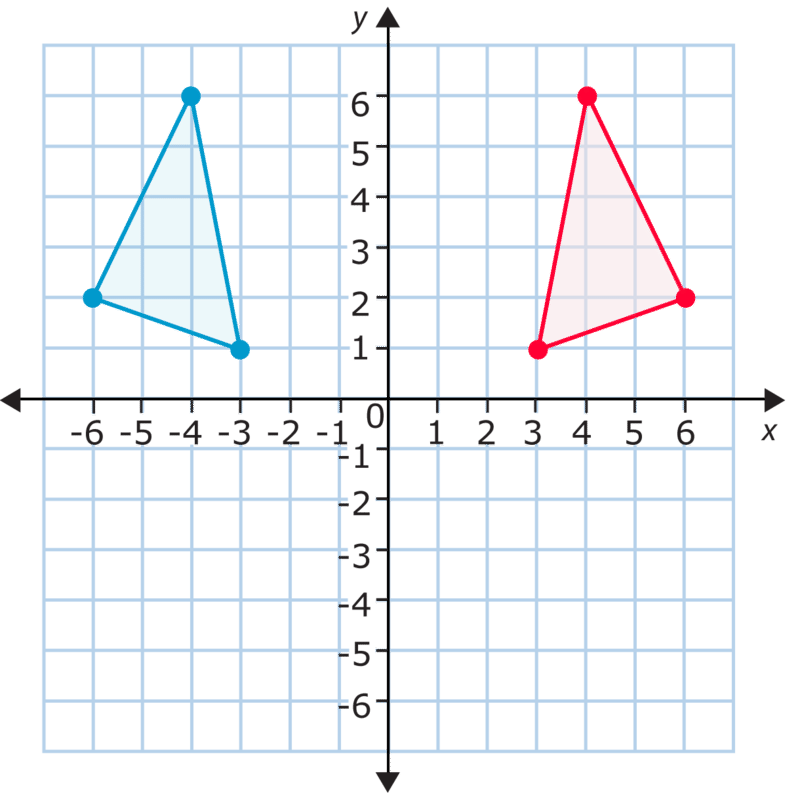
Esto es un reflejo a través del\(y\) eje. Compara los puntos. Observe que las\(y\) coordenadas −permanecen iguales. Las\(x\) coordenadas −se convierten en los opuestos enteros de las\(x\) coordenadas −originales. Mira el punto superior del triángulo, por ejemplo. Las coordenadas del punto original son\((-4, 6)\), y las coordenadas del nuevo punto son\((4, 6)\). La\(x\) coordenada −ha cambiado de -4 a 4.
Puede reconocer reflexiones por estos cambios en las\(y\) coordenadas\(x\) − y −. Si reflexiona a través del\(x\) eje −, las\(y\) coordenadas −se volverán opuestas. Si reflexionas a través del\(y\) eje, las\(x\) coordenadas −se volverán opuestas.
También puedes usar esta información para graficar reflexiones. Para graficar una reflexión, debe decidir si la reflexión se realizará a través del\(x\) eje −axis o el\(y\) eje -y luego cambiar las\(y\) coordenadas\(x\) − o −.
Ahora veamos el tercer tipo de transformación: las rotaciones. Una rotación es una transformación que gira la figura en sentido horario o antihorario. La siguiente figura ha sido rotada. ¿Cuáles son sus nuevas coordenadas?
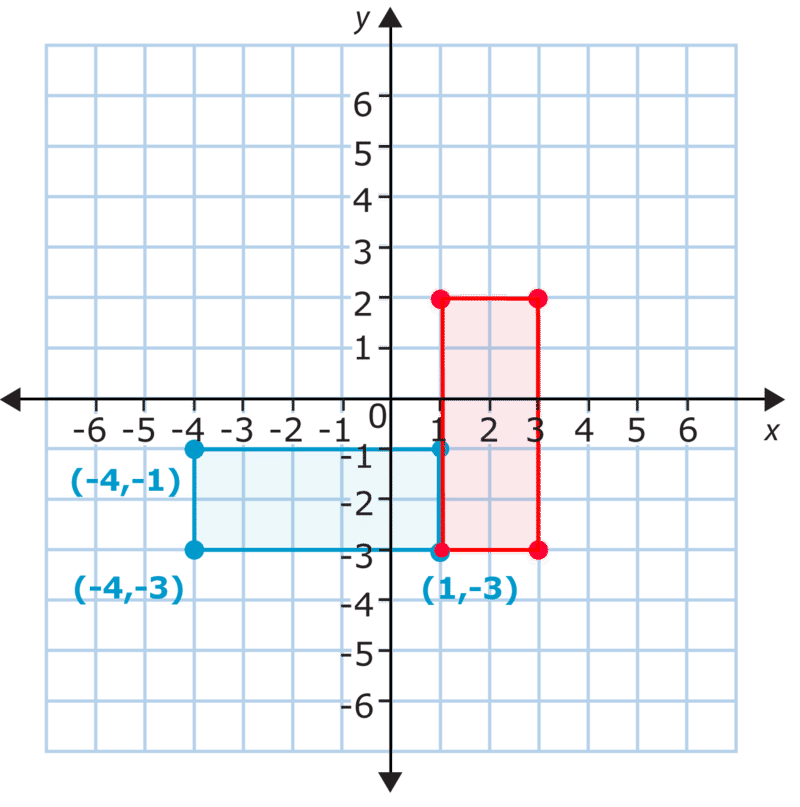
Las nuevas coordenadas de los vértices del rectángulo son\((1, -3)\),\((1, 2)\),\((3, 2)\), y\((3, -3)\). Como puede ver, las\(y\) coordenadas\(x\) − y −cambiaron. Uno de los puntos se mantuvo exactamente igual. Eso significa que la cifra se giró alrededor de este punto. Imagina que pones tu dedo en esta esquina del rectángulo y lo giras. Eso fue lo que pasó en la rotación. El rectángulo se ha girado en\(90^{\circ}\) sentido horario.
Cuando graficas una rotación, primero necesitas saber cuánto girará la figura. Al girar el rectángulo de arriba, lo\(90^{\circ}\) coloca de extremo. Girarlo lo\(180^{\circ}\) volvería a quedar plano. También necesitas saber en qué punto lo girarás. Este es el punto que se mantiene igual.
A continuación, es necesario contar cuántas unidades de largo y ancho es la cifra. La figura anterior se extiende desde 1 en el\(x\) eje −hasta -4 en el\(x\) eje −. Esto es un total de 5 unidades a lo largo del\(x\) eje −. Cuando gira una figura\(90^{\circ}\), la distancia en el\(x\) eje −se convierte en la distancia en el\(y\) eje. Mira el rectángulo. Los lados largos son horizontales al principio, pero después de girarlo, se convierten en los lados verticales. Esto significa que la distancia x de 5 se convertirá en una distancia y de 5.
Ahora, recuerda que el punto\((1, -3)\) permanece igual, por lo que es una esquina de la figura girada. Agrega 5 a la\(y\) coordenada −para encontrar el siguiente vértice del rectángulo. \(−3+5=2\). Esto pone un vértice en (1, 2)\).
Para encontrar los otros puntos del rectángulo girado, es necesario pensar en su ancho. Encuentra el ancho, o lado corto, del rectángulo original contando las unidades entre los vértices a lo largo del\(y\) eje. El rectángulo cubre 2 unidades en el\(y\) eje. Como puedes adivinar, esto se convierte en la\(x\) distancia −distancia en la figura girada. En otras palabras, se agrega 2 a la\(x\) coordenada −del punto que permanece igual. \(1+2=3\), por lo que será otro vértice del rectángulo\((3, -3)\). Para encontrar el cuarto y último vértice, agregue 2 a la\(x\) coordenada −del otro par ordenado,\((1, 2)\). Esto pone el último vértice en\((3, 2)\).
Escribe cada conjunto de coordenadas para mostrar una reflexión en el\(y\) eje.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Tyler y su foto.
Si las coordenadas originales de la imagen son\((3, 0)\),\((4, 6)\) y\((5, 1)\), ¿cuáles son las coordenadas del reflejo?
Solución
Primero, recuerde cómo reflexionar a través del\(x\) eje −axis.
Voltear la forma a través del\(x\) eje −.
A continuación, recuerda las reglas.
Las\(y\) coordenadas −cambiarán a sus opuestos enteros.
Después, escribe los nuevos puntos.
\((3, 0)\),\((4, -6)\),\((5, -1)\)
La respuesta es que las coordenadas de la reflexión son\((3, 0)\),\((4, -6)\),\((5, -1)\).
Ejemplo\(\PageIndex{2}\)
La siguiente figura se refleja a través del\(x\) eje −. ¿Cuáles son las coordenadas de la reflexión?
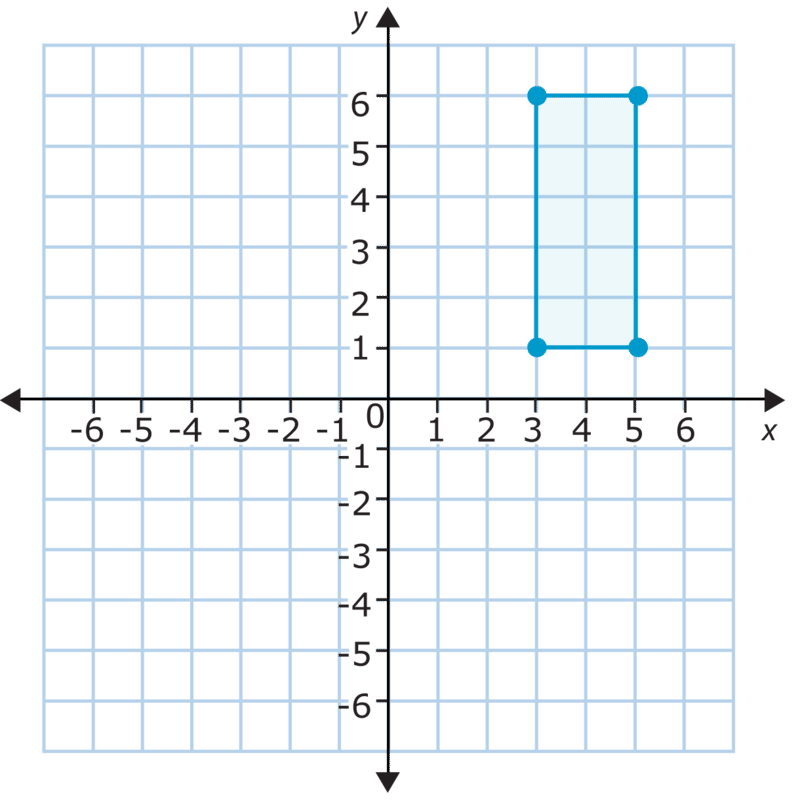
Solución
Primero, recuerde cómo reflexionar a través del\(x\) eje −axis.
Voltear la forma a través del\(x\) eje −.
A continuación, recuerda las reglas.
Las\(y\) coordenadas −cambiarán a sus opuestos enteros.
Después, escribe los nuevos puntos.
\((3, -6)\),\((3, -1)\),\((5, -6)\),\((5, -1)\)
La respuesta es que las coordenadas de la reflexión son\((3, -6)\),\((3, -1)\),\((5, -6)\),\((5, -1)\).
Ejemplo\(\PageIndex{3}\)
Determinar si el cambio es el resultado de una traslación, reflexión o rotación.
Después de una transformación, los vértices\((3, 1)\),\((0, 3)\),\((1, 2)\) se convierten\((3, -1)\),\((0, -3)\),\((1, -2)\).
Solución
Primero, mira las coordenadas para ver qué coordenadas cambian.
Las\(x\) coordenadas −permanecen iguales y las\(y\) coordenadas −cambian para cada uno de los puntos.
A continuación, determinar el tipo de cambio para las coordenadas.
Las nuevas\(y\) coordenadas −son opuestas a las coordenadas originales.
Entonces, indicar el tipo de transformación.
Reflexión
La respuesta es que el cambio es el resultado de una reflexión.
Ejemplo\(\PageIndex{4}\)
Determinar si el cambio es el resultado de una traslación, reflexión o rotación.
Después de una transformación, los vértices\((-3, 6)\),\((-2, 3)\),\((2, 3)\),\((3, 6)\) se convierten\((-3, -1)\),\((-2, 8)\),\((2, 8)\),\((3, 11)\).
Solución
Primero, mira las coordenadas para ver qué coordenadas cambian.
Las\(x\) coordenadas −permanecen iguales y las\(y\) coordenadas −cambian para cada uno de los puntos.
A continuación, determinar el tipo de cambio para las coordenadas.
Las nuevas\(y\) coordenadas −son cada una 5 más que las coordenadas originales.
Entonces, indicar el tipo de transformación.
Traducción
La respuesta es que el cambio es el resultado de una traducción.
Ejemplo\(\PageIndex{5}\)
Los puntos\((1, 2)\),\((3, 7)\),\((3, 4)\),\((5, 6)\) se reflejan sobre el\(y\) eje -eje. ¿Cuáles son las nuevas coordenadas?
Solución
Primero, recuerde los cambios que ocurren con una reflexión sobre el\(y\) eje.
Las\(x\) coordenadas −se convierten en lo contrario y las\(y\) coordenadas −permanecen iguales.
Después, escribe las nuevas coordenadas.
\((-1, 2)\),\((-3, 7)\),\((-3, 4)\),\((-5, 6)\)
La respuesta es que las nuevas coordenadas son\((-1, 2)\),\((-3, 7)\),\((-3, 4)\),\((-5, 6)\).
Verdadero o falso. Cuando hay una reflexión en el\(y\) eje, ambas coordenadas cambian a opuestas.
Revisar
Usa esta figura para responder a cada pregunta. Asegúrese de escribir todo en notación de coordenadas cuando sea posible.
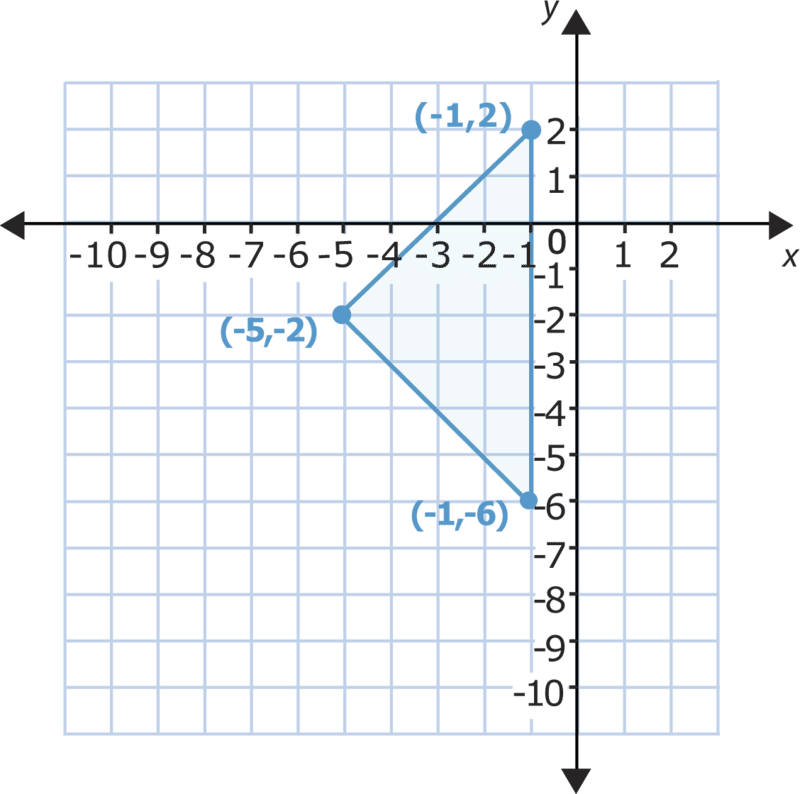
- Traduzca esta cifra tres unidades hacia arriba.
- Traduzca esta cifra cuatro unidades a la derecha.
- Traduzca esta cifra cinco unidades hacia abajo.
- Traduzca esta cifra seis unidades a la izquierda.
- Traduzca esta cifra una unidad hacia abajo y dos unidades a la derecha.
- Traduzca esta cifra dos unidades hacia arriba y una unidad a la izquierda.
- Traduzca esta cifra tres unidades hacia arriba y una unidad a la derecha.
- Girar esta figura 180 grados.
- Girar esta figura 90 grados.
- Refleja esta figura sobre el eje x.
- Refleja esta figura sobre el eje y.
- Traduzca esta cifra cinco unidades hacia arriba y tres unidades a la derecha.
- Traduzca esta cifra seis unidades hacia abajo y cuatro unidades a la izquierda.
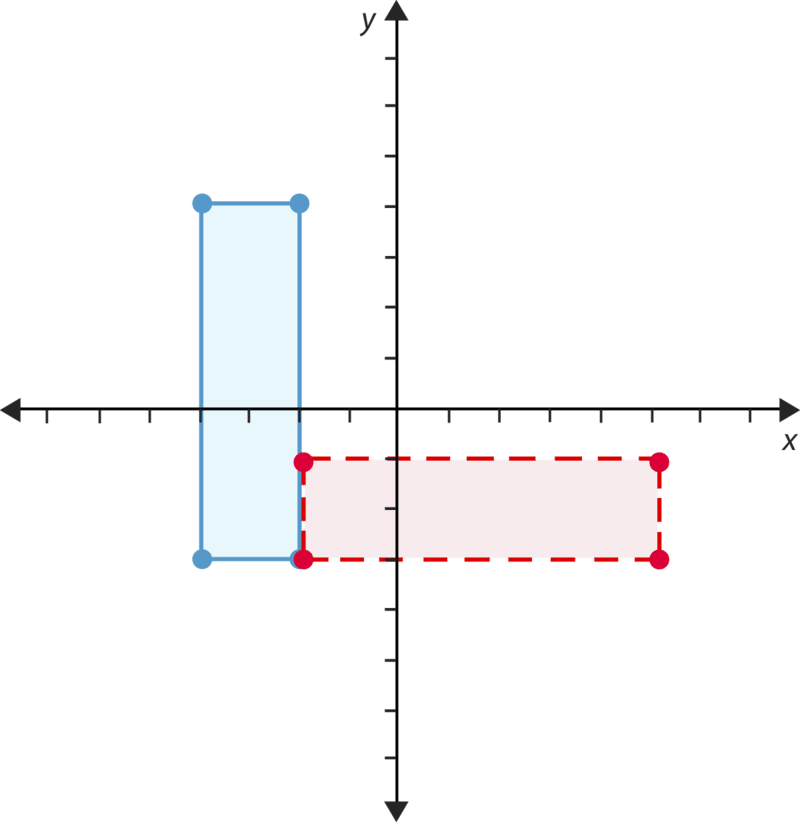
- Verdadero o falso. La siguiente figura es una imagen de un reflejo.
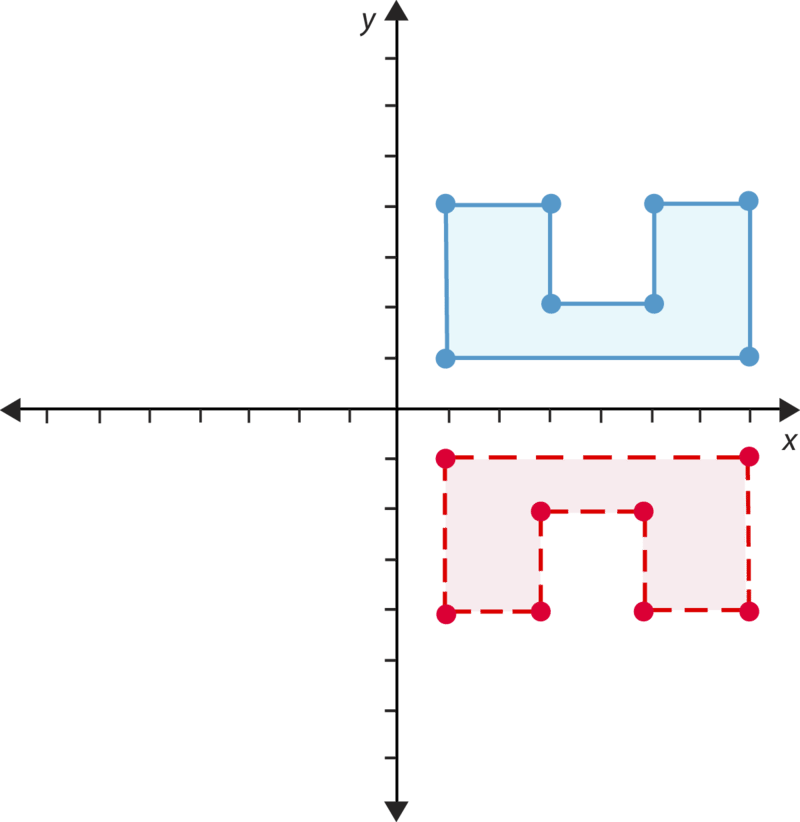
- Verdadero o falso. Esta cifra ha sido rotada\(180^{\circ}\).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.19.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| \(x\)−eje | El\(x\) eje −axis es el eje horizontal en el plano de coordenadas, que comúnmente representa el valor de la variable de entrada o independiente. |
| \(y\)-eje | El\(y\) eje -es la recta numérica vertical del plano cartesiano. |
| Notación de coordenadas | Un punto de coordenadas es la descripción de una ubicación en el plano de coordenadas. Los puntos de coordenadas se escriben comúnmente en la forma\((x, y)\) donde\(x\) está la distancia horizontal desde el origen, e y es la distancia vertical desde el origen. |
| Plano de coordenadas | El plano de coordenadas es una rejilla formada por una recta numérica horizontal y una recta numérica vertical que se cruzan en el\((0, 0)\) punto, denominado origen. El plano de coordenadas también se llama Plano Cartesiano. |
| Reflexión | Una reflexión es una transformación que voltea una figura en el plano de coordenadas a través de una línea dada sin cambiar la forma o el tamaño de la figura. |
| Rotación | Una rotación es una transformación que convierte una figura en el plano de coordenadas un cierto número de grados alrededor de un punto dado sin cambiar la forma o el tamaño de la figura. |
| Transformación | Una transformación mueve una figura de alguna manera en el plano de coordenadas. |
| Traducción | Una traslación es una transformación que desliza una figura en el plano de coordenadas sin cambiar su forma, tamaño u orientación. |
Recursos adicionales
Elemento Interactivo
Práctica: Reflejo de figuras
Mundo real: Espejo, Espejo

