8.3: Simetría de reflexión
- Page ID
- 107569
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Propiedad de una forma con una o más líneas de simetría.
Una línea de simetría es una línea que pasa a través de una figura de tal manera que divide la figura en dos mitades congruentes de tal manera que si una mitad estuviera doblada a través de la línea de simetría aterrizaría directamente encima de la otra mitad.
La simetría de reflexión está presente cuando una figura tiene una o más líneas de simetría. Estas figuras tienen simetría de reflexión:
Estas cifras no tienen simetría de reflexión:
¿Y si tuvieras una estrella de seis puntas, trazaste una línea hacia abajo y luego la doblaste a lo largo de esa línea? Si los dos lados de la estrella se alinearan, ¿qué significaría eso de la línea?
Ejemplo\(\PageIndex{1}\)
Encuentra todas las líneas de simetría para la forma a continuación.
Solución
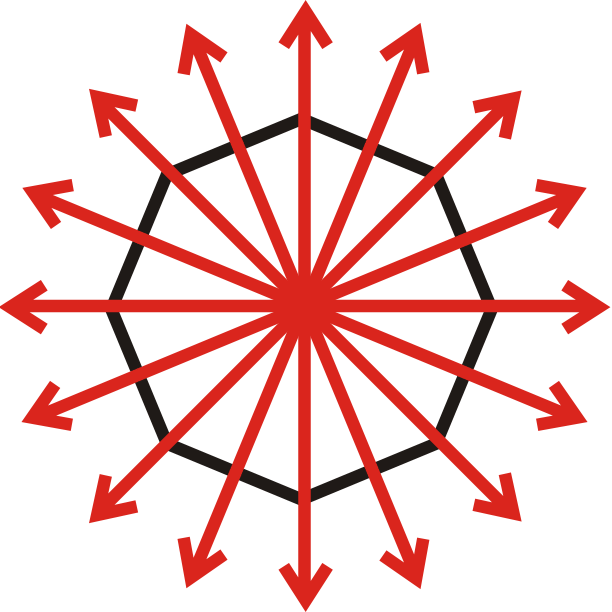
Dibuja líneas a través de la figura para que las líneas corten perfectamente la figura por la mitad. Esta figura tiene ocho líneas de simetría.
Ejemplo\(\PageIndex{2}\)
Encuentra todas las líneas de simetría para la forma a continuación.
Solución
No se pueden trazar líneas a través de la figura para que las líneas corten perfectamente la figura por la mitad, por lo que esta figura no tiene líneas de simetría.
Ejemplo\(\PageIndex{3}\)
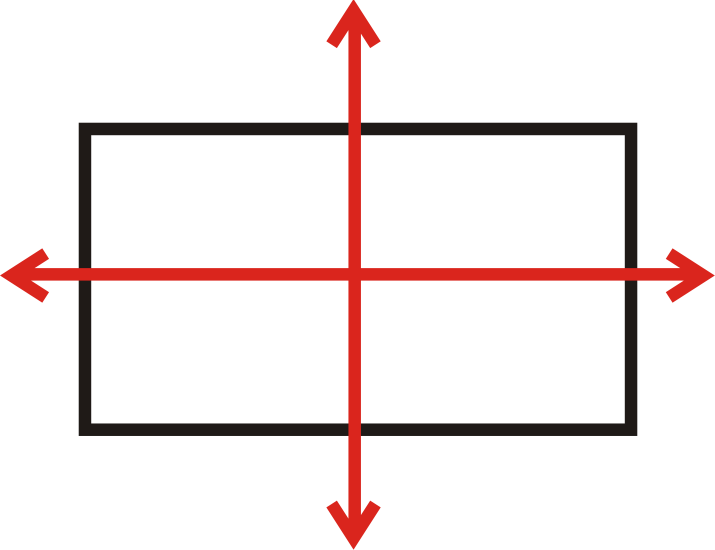
Encuentra todas las líneas de simetría para la forma a continuación.
Solución
Esta figura tiene dos líneas de simetría.
Ejemplo\(\PageIndex{4}\)
¿La siguiente figura tiene simetría de reflexión?
Solución
Sí, esta figura tiene simetría de reflexión.
Ejemplo\(\PageIndex{5}\)
¿La siguiente figura tiene simetría de reflexión?
Solución
Sí, esta figura tiene simetría de reflexión.
Revisar
Determinar si cada declaración es verdadera o falsa.
- Todos los triángulos correctos tienen simetría de línea.
- Todos los triángulos isósceles tienen simetría de línea.
- Cada rectángulo tiene simetría de línea.
- Cada rectángulo tiene exactamente dos líneas de simetría.
- Cada paralelogramo tiene simetría de línea.
- Cada cuadrado tiene exactamente dos líneas de simetría.
- Cada polígono regular tiene tres líneas de simetría.
- Cada sector de un círculo tiene una línea de simetría.
Dibuja las siguientes figuras.
- Un cuadrilátero que tiene dos pares de lados congruentes y exactamente una línea de simetría.
- Una figura con infinitamente muchas líneas de simetría.
Encuentra todas las líneas de simetría para las letras a continuación.
-
Figura\(\PageIndex{13}\) -
Figura\(\PageIndex{14}\) -
Figura\(\PageIndex{15}\) -
Figura\(\PageIndex{16}\) -
Figura\(\PageIndex{17}\)
Determinar si las siguientes palabras tienen simetría de reflexión.
- OHIO
- MOW
- WOW
- KICK
- pod
Traza cada figura y luego dibuja en todas las líneas de simetría.
-
Figura\(\PageIndex{18}\) -
Figura\(\PageIndex{19}\) -
Figura\(\PageIndex{20}\)
Determinar si las figuras a continuación tienen simetría de reflexión. Identificar todas las líneas de simetría.
-
Figura\(\PageIndex{13}\) -
Figura\(\PageIndex{13}\) -
Figura\(\PageIndex{13}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 12.1.
El vocabulario
| Término | Definición |
|---|---|
| Línea de simetría | Una línea de simetría es una línea que se puede dibujar para dividir una figura en mitades iguales. |
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| Triángulo Isósceles | Un triángulo isósceles es un triángulo en el que exactamente dos lados tienen la misma longitud. |
| Simetría de línea | Una figura tiene simetría de línea o simetría de reflexión cuando se puede dividir en mitades iguales que coinciden. |
| simetría de reflexión | Una figura tiene simetría de reflexión si se puede reflejar a través de una línea y se ve exactamente igual que antes de la reflexión. |
| Simetría | Una figura tiene simetría si se puede transformar y seguir luciendo igual. |
Recursos adicionales
Elemento interactivo
Video: Principios de simetría de reflexión - Básico
Actividades: Reflexión Simetría Discusión Preguntas
Ayudas de estudio: Guía de estudio de simetría y teselaciones
Práctica: Simetría de reflexión