8.10: Definición de Rotación
- Page ID
- 107623
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Transformaciones mediante las cuales una figura se gira alrededor de un punto fijo para crear una imagen.
Rotaciones
Una transformación es una operación que mueve, voltea o cambia de otra manera una figura para crear una nueva figura. Una transformación rígida (también conocida como transformación de isometría o congruencia) es una transformación que no cambia el tamaño o la forma de una figura.
Las transformaciones rígidas son traslaciones, reflexiones y rotaciones. La nueva figura creada por una transformación se llama la imagen. La figura original se llama la preimagen. Si la preimagen es\(A\), entonces la imagen sería\(A′\), dijo “un primo”. Si hay una imagen de\(A′\), eso sería etiquetado\(A′′\), dijo “un doble primo”.
Una rotación es una transformación donde una figura se gira alrededor de un punto fijo para crear una imagen. Las líneas dibujadas desde la preimagen hasta el centro de rotación y desde el centro de rotación a la imagen forman el ángulo de rotación.
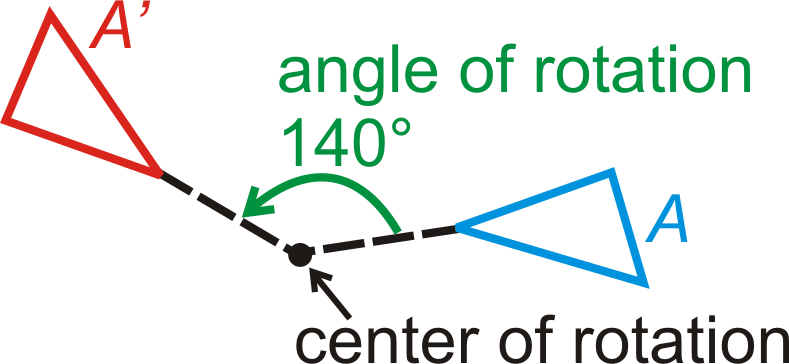
Si bien podemos rotar cualquier imagen cualquier cantidad de grados,\(90^{\circ}\),\(180^{\circ}\) y\(270^{\circ}\) las rotaciones son comunes y tienen reglas que vale la pena memorizar.
Rotación de\(180^{\circ}\):\((x,y)\rightarrow (−x,−y)\)
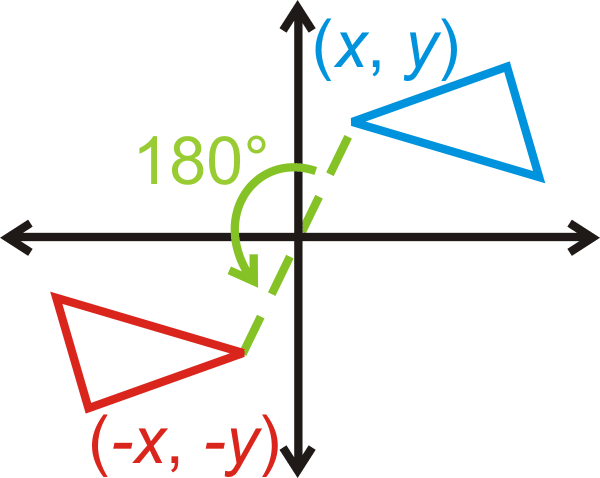
Rotación de\(90^{\circ}\):\((x,y)\rightarrow (−y,x)\)
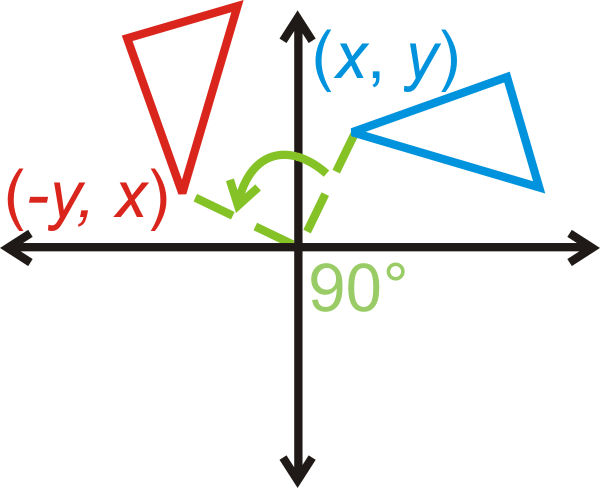
Rotación de\(270^{\circ}\):\((x,y)\rightarrow (y,−x)\)
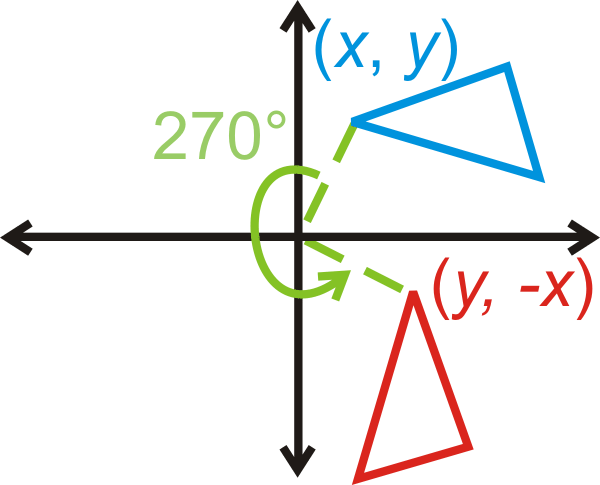
¿Y si te dieran las coordenadas de un cuadrilátero y te pidieran rotar ese cuadrilátero\(270^{\circ}\) sobre el origen? ¿Cuáles serían sus nuevas coordenadas?
Ejemplo\(\PageIndex{1}\)
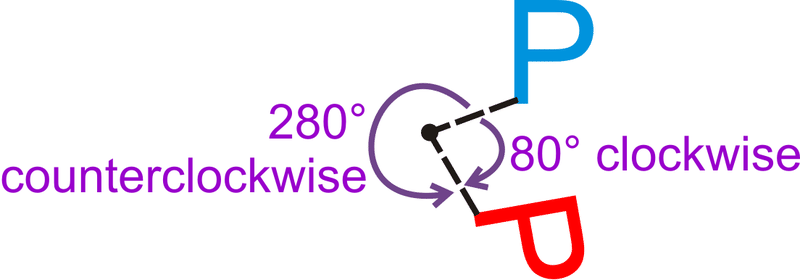
Una rotación de\(80^{\circ}\) las agujas del reloj es lo mismo que la rotación en sentido antihorario?
Solución
Hay\(360^{\circ}\) alrededor de un punto. Entonces, una\(80^{\circ}\) rotación en sentido horario es lo mismo que una\(360^{\circ}−80^{\circ}=280^{\circ}\) rotación en sentido antihorario.
Figura\(\PageIndex{6}\)Ejemplo\(\PageIndex{2}\)
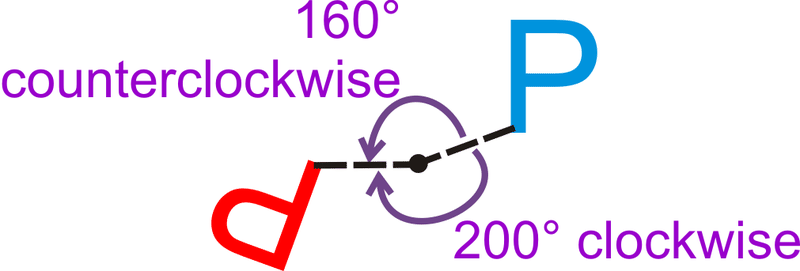
Una rotación de\ (160^ {\ circ} en sentido contrario a las agujas del reloj es lo mismo que la rotación en sentido horario?
Solución
\(360^{\circ}−160^{\circ}=200^{\circ}\)rotación en sentido horario.
Ejemplo\(\PageIndex{3}\)
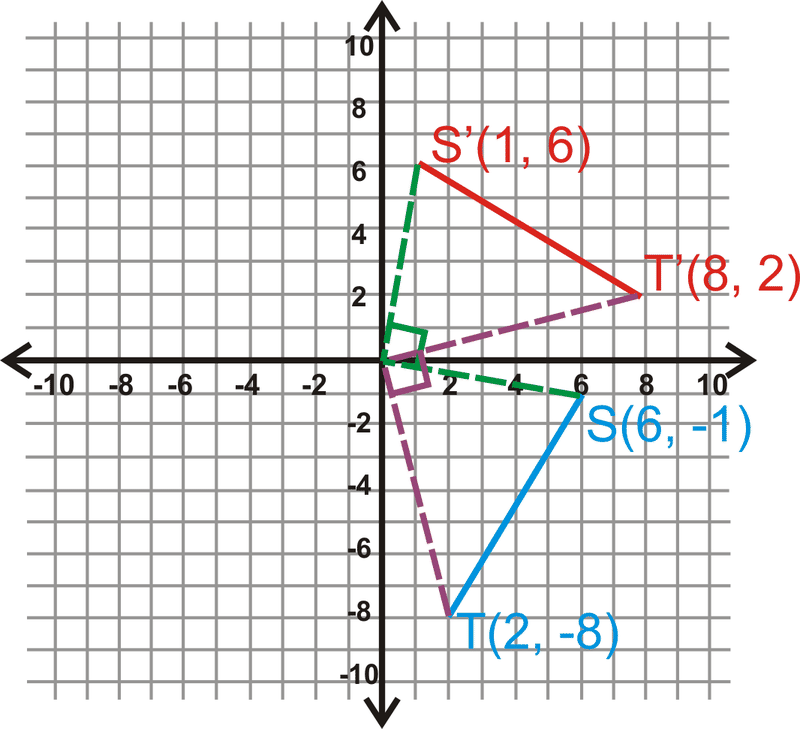
Rotar\(\overline{ST} 90^{\circ}\).
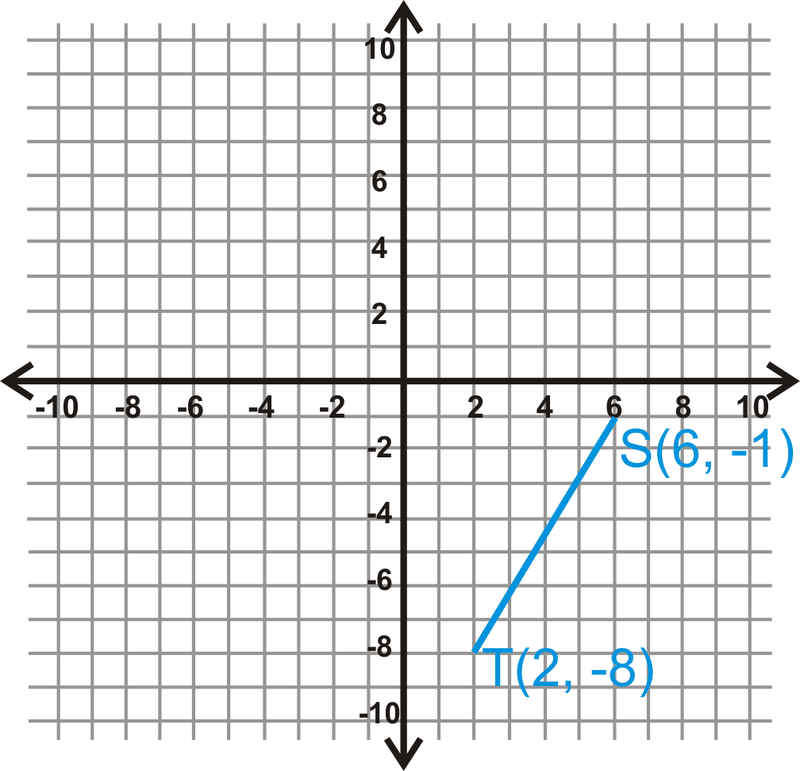
Solución
Ejemplo\(\PageIndex{4}\)
A continuación se muestra la rotación de un cuadrilátero. ¿Cuál es la medida de\(x\) y\(y\)?
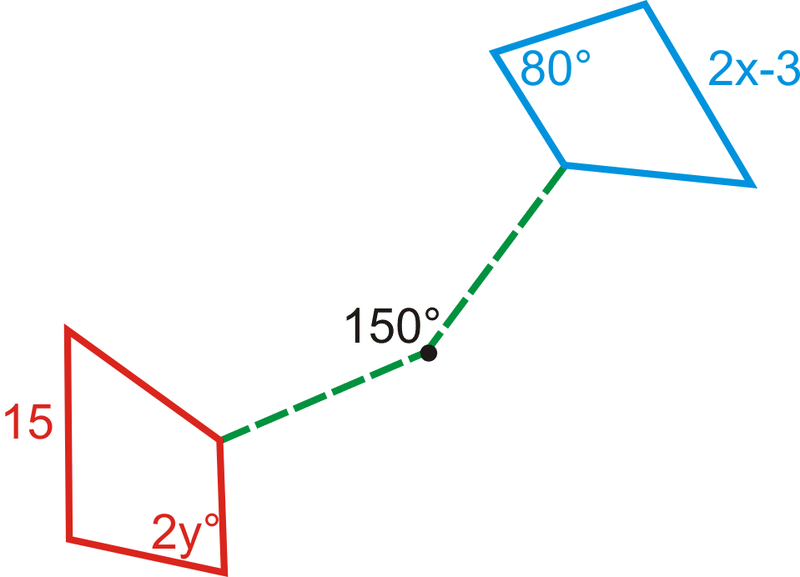
Solución
Debido a que una rotación produce cifras congruentes, podemos establecer dos ecuaciones para resolver para\(x\) y\(y\).
\ (y=4\ begin {array} {rr}
2 y=80^ {\ circ} & 2 x-3=15\
y=40^ {\ circ} & 2 x=18\
& x=9
\ end {array}\)
Ejemplo\(\PageIndex{5}\)
Rotar\(\Delta ABC\), con vértices\(A(7,4)\)\(B(6,1)\), y\(C(3,1)\),\(180^{\circ}\) sobre el origen. Encuentra las coordenadas de\(\Delta A′B′C′\).
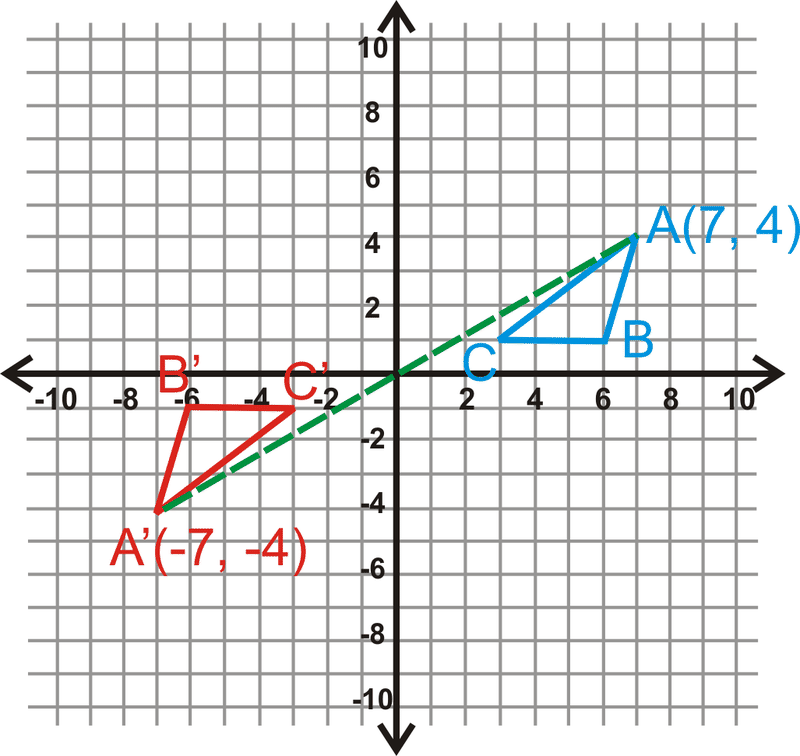
Solución
Usa la regla anterior para encontrar\(\Delta A′B′C′\).
\(\begin{aligned}A(7,4)&\rightarrow A′(−7,−4) \\ B(6,1)&\rightarrow B′(−6,−1) \\ C(3,1)&\rightarrow C′(−3,−1)\end{aligned}\)
Revisar
En las preguntas siguientes, cada rotación es en sentido antihorario, a menos que se indique lo contrario.
- Si rotaste la letra p 180^ {\ circ}\) en sentido contrario a las agujas del reloj, ¿qué letra tendrías?
- Si rotaste la letra p\(180^{\circ}\) c\ (ockwise, ¿qué letra tendrías?
- Una rotación\(90^{\circ}\) en sentido horario es lo mismo que la rotación en sentido antihorario?
- Una rotación\(270^{\circ}\) en sentido horario es lo mismo que la rotación en sentido antihorario?
- Una rotación\(210^{\circ}\) en sentido antihorario es lo mismo que la rotación en sentido horario?
- Una rotación\(120^{\circ}\) en sentido antihorario es lo mismo que la rotación en sentido horario?
- Una rotación\(340^{\circ}\) en sentido antihorario es lo mismo que la rotación en sentido horario?
- Girar una figura\(360^{\circ}\) es lo mismo que otra rotación?
- ¿Importa si giras una figura en\(180^{\circ}\) sentido horario o antihorario? ¿Por qué o por qué no?
- Al dibujar una figura girada y usar tu traslador, ¿sería más fácil rotar la figura en\(300^{\circ}\) sentido antihorario o en\(60^{\circ}\) sentido horario? Explica tu razonamiento.
Gire cada figura en el plano de coordenadas la medida del ángulo dado. El centro de rotación es el origen.
- \(180^{\circ}\)
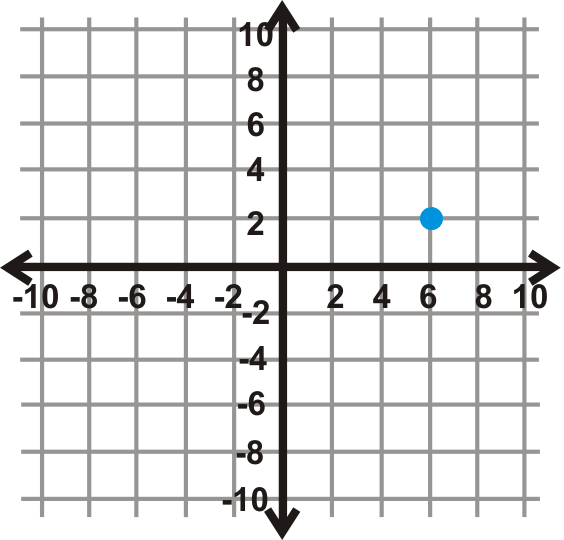
Figura\(\PageIndex{12}\) - \(90^{\circ}\)
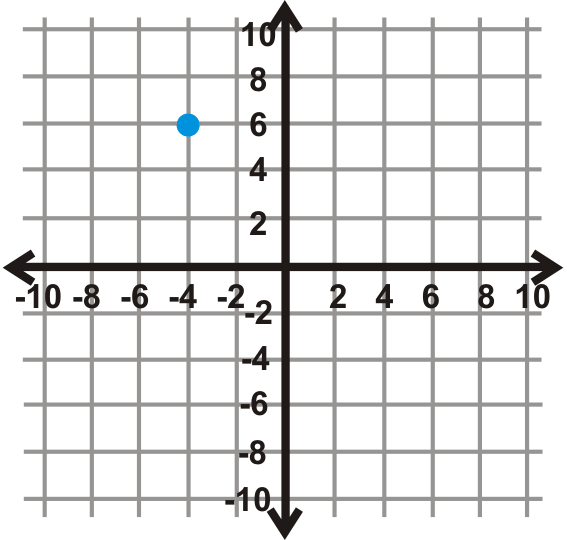Figura\(\PageIndex{13}\) - \(180^{\circ}\)
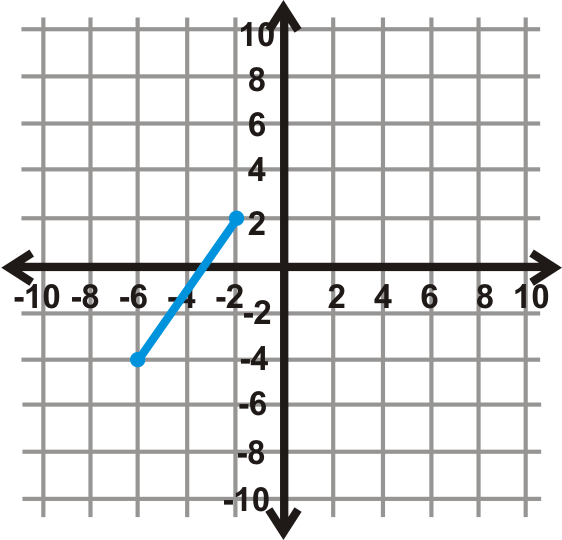
Figura\(\PageIndex{14}\) - \(270^{\circ}\)
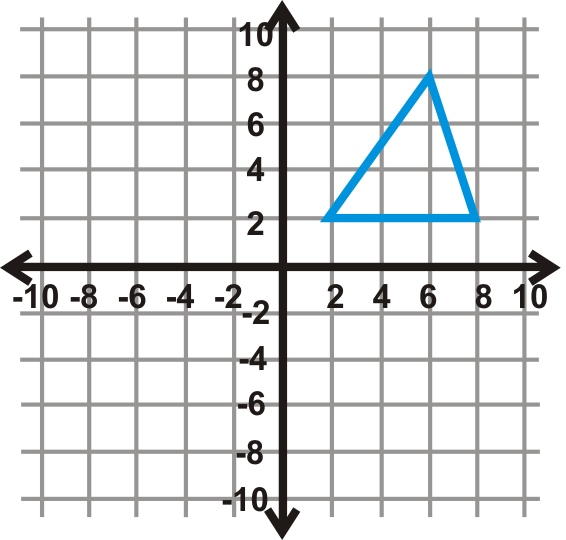
Figura\(\PageIndex{15}\) - \(90^{\circ}\)
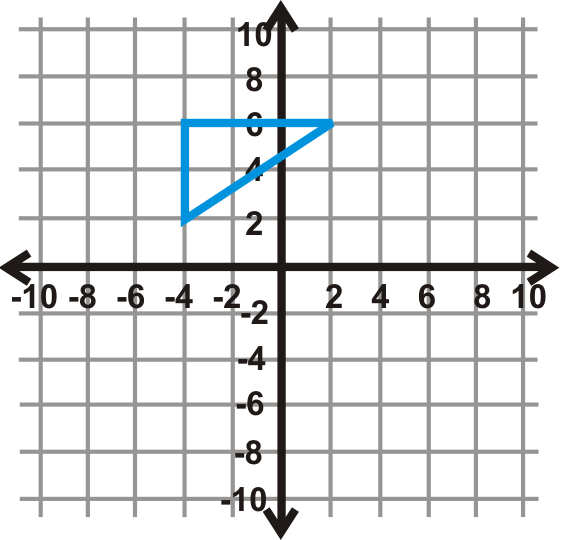
Figura\(\PageIndex{16}\) - \(270^{\circ}\)
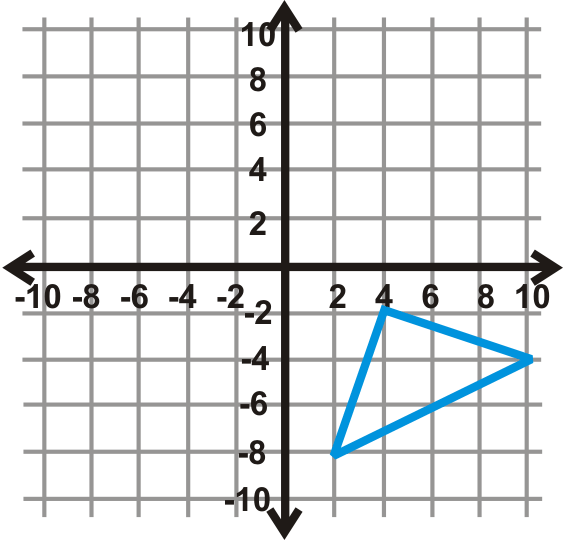
Figura\(\PageIndex{17}\) - \(180^{\circ}\)
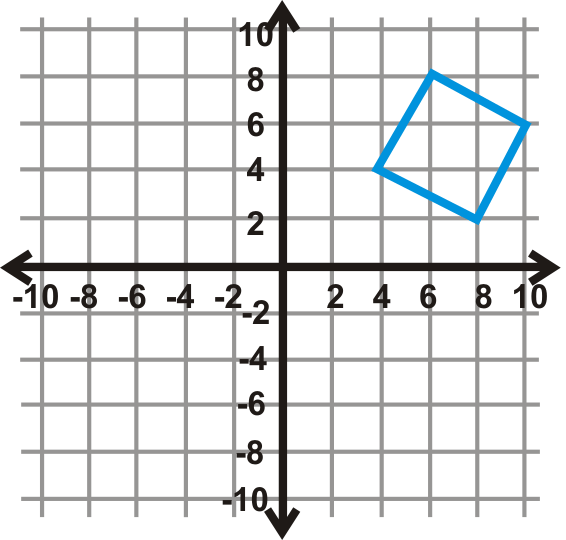
Figura\(\PageIndex{18}\) - \(270^{\circ} \)
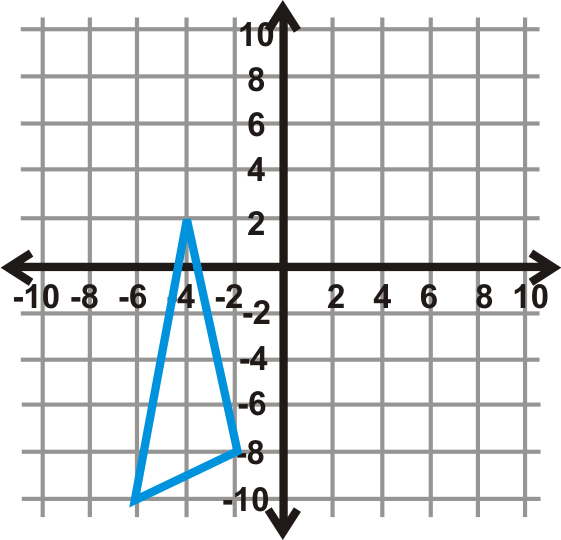
Figura\(\PageIndex{19}\) - \(90^{\circ} \)
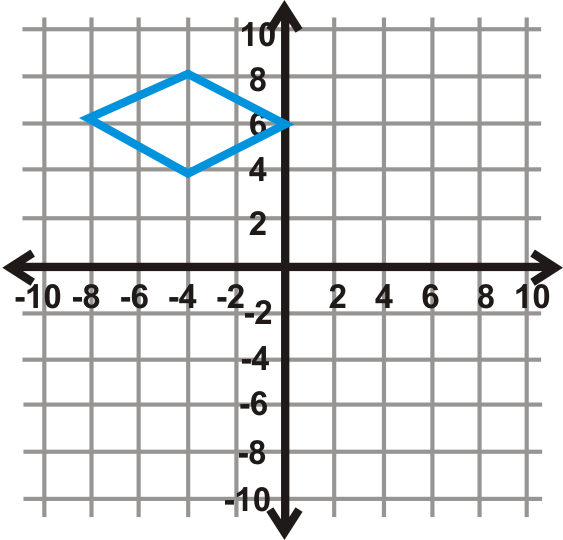
Figura\(\PageIndex{20}\)
Encuentre la medida de\(x\) en las rotaciones a continuación. La figura azul es la preimagen.
-
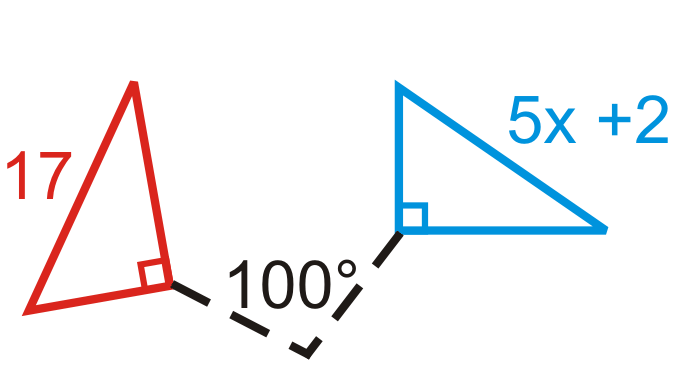
Figura\(\PageIndex{21}\) -
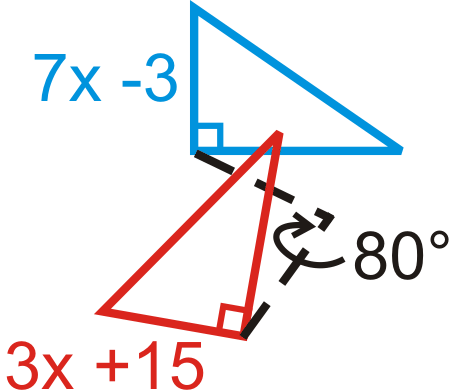
Figura\(\PageIndex{22}\) -
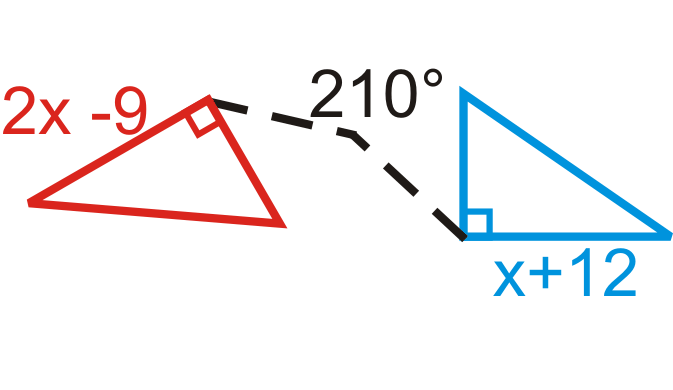
Figura\(\PageIndex{23}\)
Encuentre el ángulo de rotación para las gráficas a continuación. El centro de rotación es el origen y la figura azul es la preimagen. Tu respuesta será\(90^{\circ}\),\(270^{\circ}\), o\(180^{\circ}\).
-
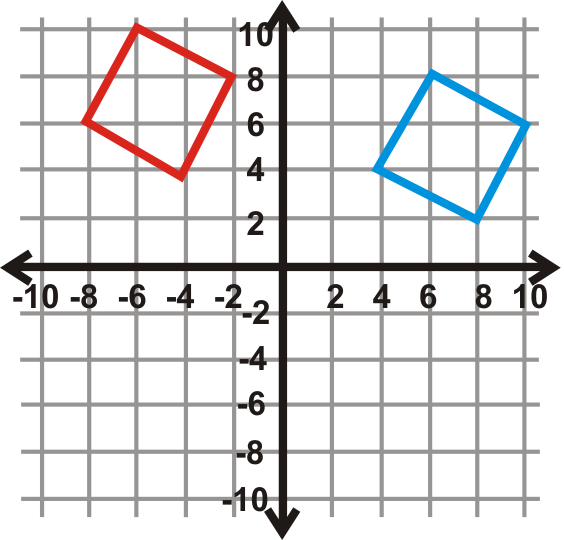
Figura\(\PageIndex{24}\) -
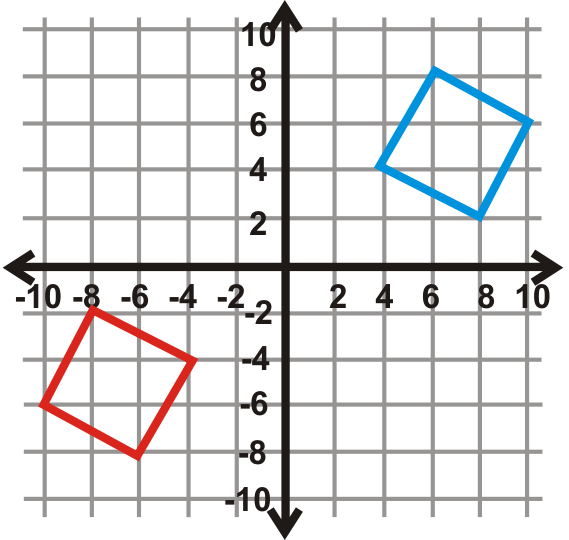
Figura\(\PageIndex{25}\) -
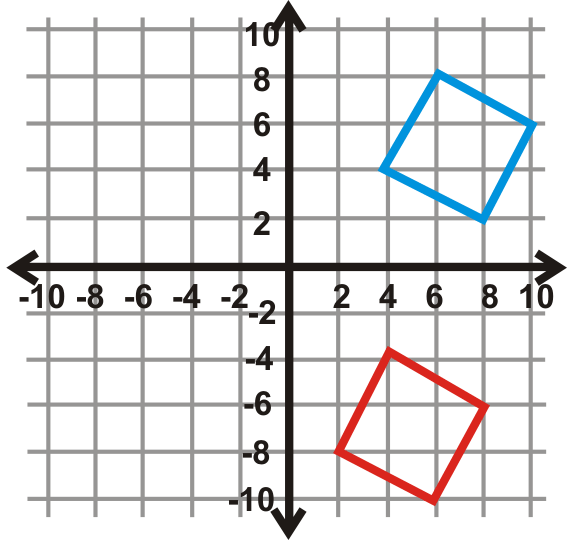
Figura\(\PageIndex{26}\) -
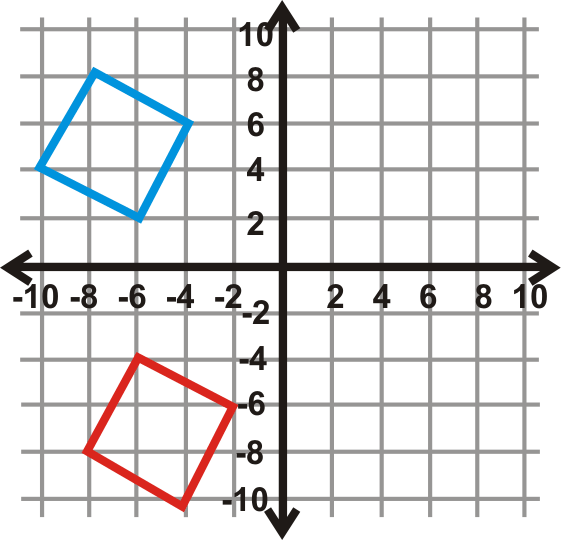
Figura\(\PageIndex{27}\) -
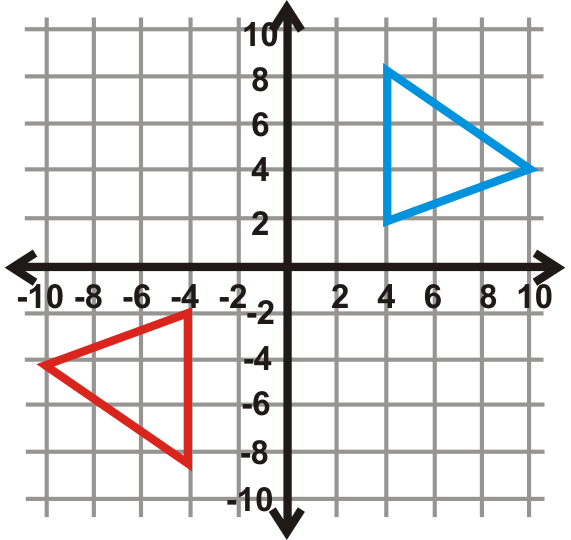
Figura\(\PageIndex{28}\) -
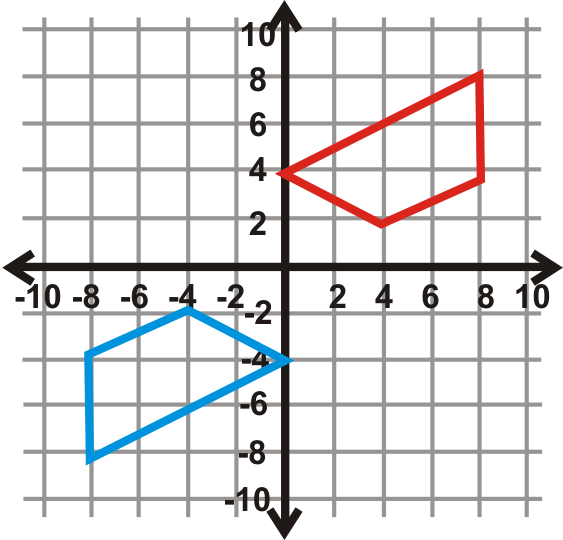
Figura\(\PageIndex{29}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 12.4.
El vocabulario
| Término | Definición |
|---|---|
| Centro de Rotación | En una rotación, el centro de rotación es el punto que no se mueve. El resto del plano gira alrededor de este punto fijo. |
| Imagen | La imagen es la apariencia final de una figura después de una operación de transformación. |
| Origen | El origen es el punto de intersección de los ejes x e y en el plano cartesiano. Las coordenadas del origen son (0, 0). |
| Preimagen | La pre-imagen es la apariencia original de una figura en una operación de transformación. |
| Rotación | Una rotación es una transformación que convierte una figura en el plano de coordenadas un cierto número de grados alrededor de un punto dado sin cambiar la forma o el tamaño de la figura. |
| Transformación Rígida | Una transformación rígida es una transformación que conserva la distancia y los ángulos, no cambia el tamaño ni la forma de la figura. |
Recursos adicionales
Elemento Interactivo
Video: Transformación: Principios de Rotación - Básicos
Actividades: Rotaciones Discusión Preguntas
Ayudas de estudio: Guía de estudio de tipos de transformaciones
Práctica: Definición de Rotación
Mundo real: Rotaciones radicales