8.14: Reglas para Reflexiones

Identificar y establecer reglas que describen reflexiones usando notación

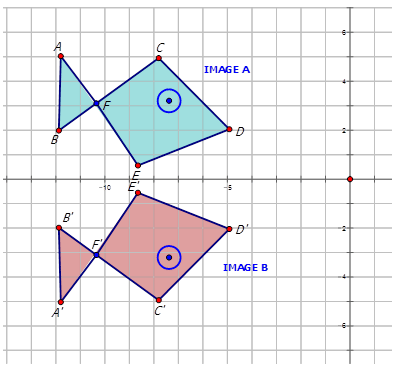
La siguiente figura muestra un patrón de dos peces. Escribe la regla de mapeo para el reflejo de Imagen\(A\) a Imagen\(B\).

Figura\(\PageIndex{1}\)

En geometría, una transformación es una operación que mueve, voltea o cambia una forma para crear una nueva forma. Una reflexión es un ejemplo de una transformación que toma una forma (llamada preimagen) y la voltea a través de una línea (llamada línea de reflexión) para crear una nueva forma (llamada imagen). Al examinar las coordenadas de la imagen reflejada, se puede determinar la línea de reflexión. Las líneas de reflexión más comunes son el\(x\) eje -eje, el\(y\) -eje, o las líneas\(y=x\) o\(y=−x\).

Figura\(\PageIndex{2}\)

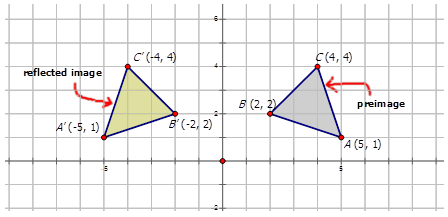
La preimagen anterior se ha reflejado a través del\(y\) eje. Esto significa que todas las coordenadas x se han multiplicado por -1. Se puede describir la reflexión en palabras, o con la siguiente notación:

\(r_{y-axis} (x,y)\rightarrow (−x,y)\)

Observe que la notación le indica exactamente cómo cambia cada\((x,y)\) punto como resultado de la transformación.

Encontremos la imagen del punto\((3, 2)\) que ha sufrido una reflexión a través de las siguientes líneas:

1. El\(x\) eje -,

Reflexión a través del\(x\) eje:\(r_{x-axis} (3,2)\rightarrow (3,−2)\)

2. El\(y\) eje

Reflexión a través del\(y\) eje:\(r_{y-axis} (3,2)\rightarrow (3,−2)\)

3. La línea\(y=x\)

Reflexión a través de la línea\(y=x\):\(r_{y=x} (3,2)\rightarrow (2,3)\)

4. La línea\(y=−x\).

Reflexión a través de la línea\(y=−x\):\(r_{y=−x} (3,2)\rightarrow (−2,−3)\)

Figura\(\PageIndex{4}\)

Ahora, reflejemos Imagen\(A\) en el diagrama a continuación a través de las siguientes líneas y escribamos la notación para cada reflexión:

Figura\(\PageIndex{5}\)

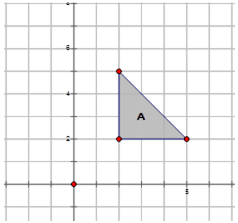
1. A través del\(y\) eje y etiquetarlo\(B\).

Reflexión a través del\(y\) eje:\(r_{y-axis} A\rightarrow B=r_{y-axis} (x,y)\rightarrow (−x,y)\)

2. A través del\(x\) eje y etiquetarlo\(O\).

Reflexión a través del\(x\) eje:\(r_{x-axis} A\rightarrow O=r_{x-axis} (x,y)\rightarrow (x,−y)\)

3. Al otro lado de la línea\(y=−x\) y etiquetarlo\(Z\).

Reflexión a través de\(y=−x\):\(r_{y=−x} A\rightarrow Z=r_{y=−x} (x,y)\rightarrow (−y,−x) \)

Figura\(\PageIndex{6}\)

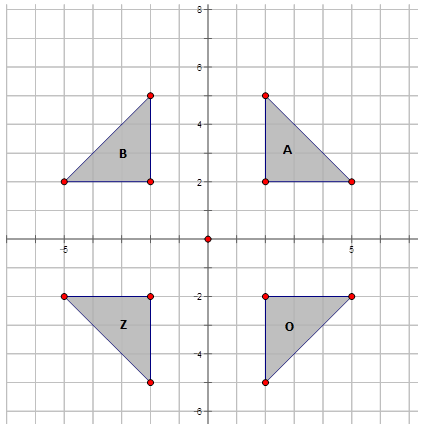
Finalmente, escribamos la notación que representa el reflejo de la preimagen a la imagen en el siguiente diagrama:

Figura\(\PageIndex{7}\)

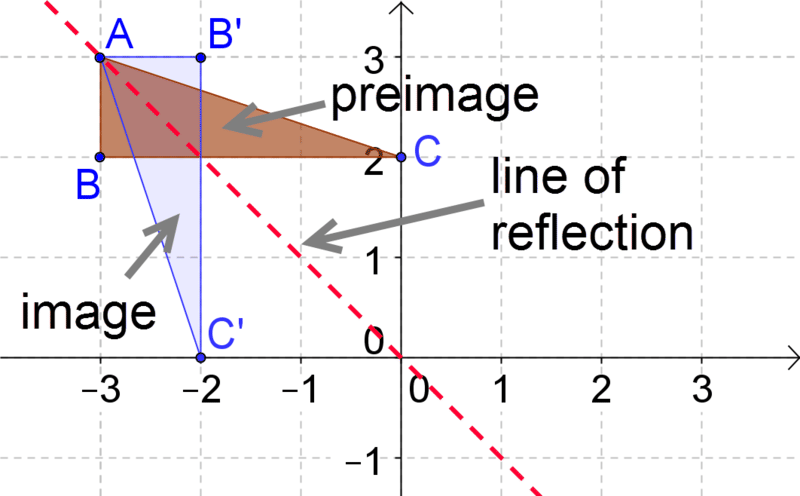
Esto es un reflejo a través de la línea\(y=−x\). La notación es\(r_{y=−x} (x,y)\rightarrow (−y,−x)\).

Ejemplo\(\PageIndex{1}\)

Anteriormente, se le dio un problema sobre la figura de abajo que muestra un patrón de dos peces. Escriba la regla de mapeo para el reflejo de la Imagen A\) a la Imagen B\).

Figura\(\PageIndex{8}\)

Solución

Para responder a esta pregunta, mira los puntos de coordenadas para la Imagen A y la Imagen B.

Imagen A	\(A(−11.8,5)\)	\(B(−11.8,2)\)	\(C(−7.8,5)\)	\(D(−4.9,2)\)	\(E(−8.7,0.5)\)	\(F(−10.4,3.1)\)
Imagen B	\(A′(−11.8,−5)\)	\(B′(−11.8,−2)\)	\(C′(−7.8,−5)\)	\(D′(−4.9,−2)\)	\(E′(−8.7,−0.5)\)	\(F′(−10.4,−3.1)\)

Observe que todo el\(y-coordinates have changed sign. Therefore Image A has reflected across the \(x\) eje -. Para escribir una regla para esta reflexión escribirías:\(r_{x-axis} (x,y)\rightarrow (x,−y)\).

Ejemplo\(\PageIndex{2}\)

Thomas describe una reflexión como punto\(J moving from \(J(−2,6)\) a\(J′(−2,−6)\). Escribe la notación para describir esta reflexión para Tomás.

\(J:(−2,6)\qquad J′:(−2,−6)\)

Solución

Dado que la coordenada y se multiplica por -1 y el\(x-coordinate remains the same, this is a reflection in the \(x\) eje -. La notación es:\(r_{x-axis} J\rightarrow J′=r_{x-axis} (−2,6)\rightarrow (−2,6)\)

Ejemplo\(\PageIndex{3}\)

Escribe la notación que representa el reflejo del diamante amarillo al diamante verde reflejado en el diagrama de abajo.

Figura\(\PageIndex{9}\)

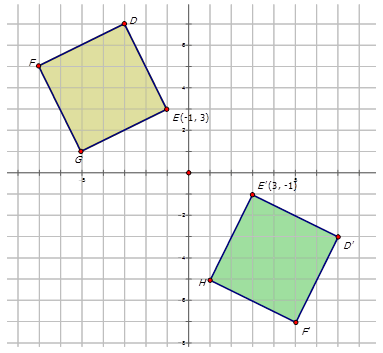
Solución

Para escribir la notación para describir el reflejo, elija un punto en la preimagen (el diamante amarillo) y luego el punto reflejado en el diamante verde para ver cómo se ha movido el punto. Observe que el punto\(E\) se muestra en el diagrama:

\(E(−1,3)\rightarrow E′(3,−1)\)

Dado que ambas\(y\) coordenadas\(x\) - y -son números invertidos, la reflexión está en la línea\(y=x\). La notación para esta reflexión sería:\(r_{y=x} (x,y)\rightarrow (y,x)\).

Ejemplo\(\PageIndex{4}\)

Karen estaba jugando con un programa de dibujo en su computadora. Ella creó los siguientes diagramas y luego quiso determinar las transformaciones. Escribe la regla de notación que representa la transformación del diagrama púrpura y azul al diagrama naranja y azul.

Figura\(\PageIndex{10}\)

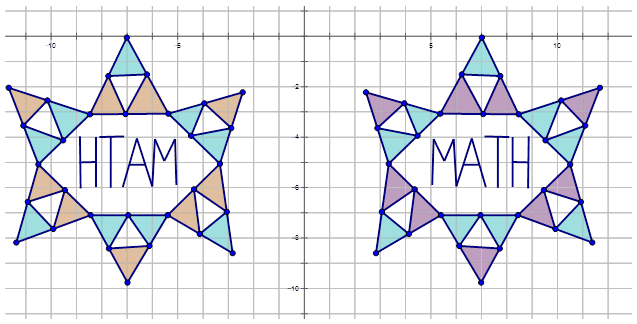
Solución

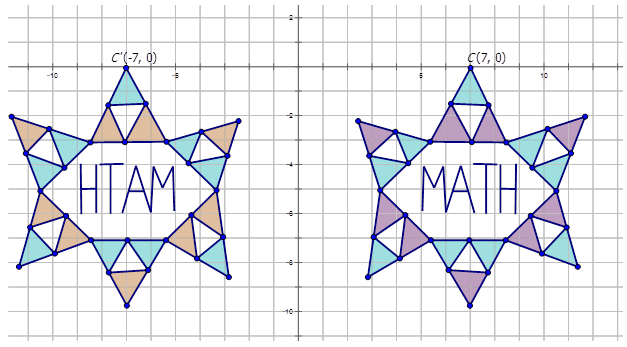
Para escribir la notación para describir la transformación, elija un punto en la preimagen (diagrama púrpura y azul) y luego el punto transformado en el diagrama naranja y azul para ver cómo se ha movido el punto. Observe que el punto A se muestra en el diagrama:

\(C(7,0)\rightarrow C′(−7,0)\)

Dado que ambas coordenadas x sólo se multiplican por -1, la transformación es una reflexión está en\(y\) -eje. La notación para esta reflexión sería:\(r_{y-axis} (x,y)\rightarrow (−x,y)\).

Figura\(\PageIndex{11}\)

Revisar

Escribe la notación para describir el movimiento de los puntos en cada una de las reflexiones a continuación.

1. \(S(1,5)\rightarrow S′(−1,5)\)
2. \(W(−5,−1)\rightarrow W′(5,−1)\)
3. \(Q(2,−5)\rightarrow Q′(2,5)\)
4. \(M(4,3)\rightarrow M′(−3,−4)\)
5. \(B(−4,−2)\rightarrow B′(−2,−4)\)
6. \(A(3,5)\rightarrow A′(−3,5)\)
7. \(C(1,2)\rightarrow C′(2,1)\)
8. \(D(2,−5)\rightarrow D′(5,−2)\)
9. \(E(3,1)\rightarrow E′(−3,1)\)
10. \(F(−4,2)\rightarrow F′(−4,−2)\)
11. \(G(1,3)\rightarrow G′(1,−3)\)

Escribe la notación que representa el reflejo de la imagen de preimagen para cada diagrama a continuación.

12. 

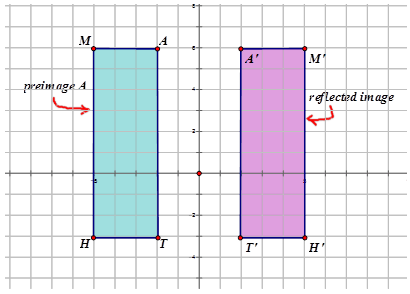
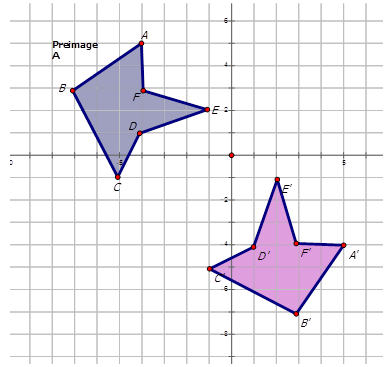
    Figura\(\PageIndex{12}\)

13. 

    Figura\(\PageIndex{13}\)

14. 

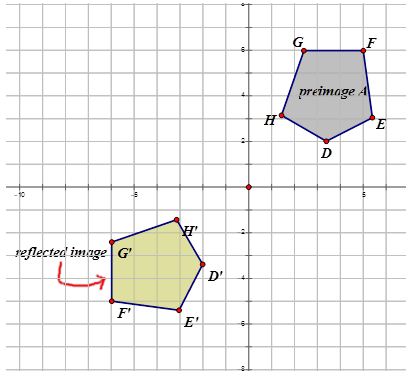
    Figura\(\PageIndex{14}\)

15. 

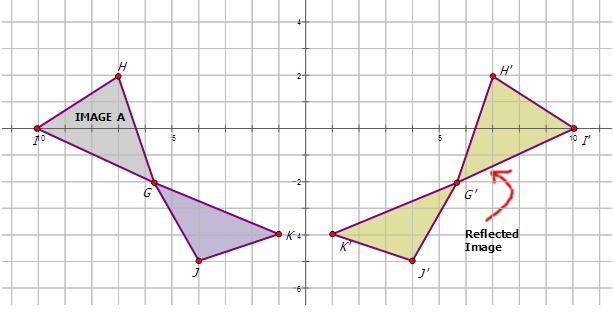
    Figura\(\PageIndex{15}\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.6.

Recursos adicionales

Elemento interactivo

Práctica: Reglas para Reflexiones