8.17: Transformaciones compuestas
- Page ID
- 107586
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Aprende a componer transformaciones de una figura en un plano de coordenadas, y entender el orden en el que aplicarlas.
Resumen de Transformaciones
Una transformación es una operación que mueve, voltea o cambia de otra manera una figura para crear una nueva figura. Una transformación rígida (también conocida como transformación de isometría o congruencia) es una transformación que no cambia el tamaño o la forma de una figura. La nueva figura creada por una transformación se llama la imagen. La figura original se llama la preimagen.
Hay tres transformaciones rígidas: traslaciones, rotaciones y reflexiones. Una traslación es una transformación que mueve cada punto de una figura a la misma distancia en la misma dirección. Una rotación es una transformación donde una figura se gira alrededor de un punto fijo para crear una imagen. Un reflejo es una transformación que convierte una figura en su imagen especular volteándola sobre una línea.
Composición de las Transformaciones
Una composición (de transformaciones) es cuando se realiza más de una transformación en una figura. Las composiciones siempre se pueden escribir como una sola regla. Puedes componer cualquier transformación, pero estas son algunas de las composiciones más comunes:
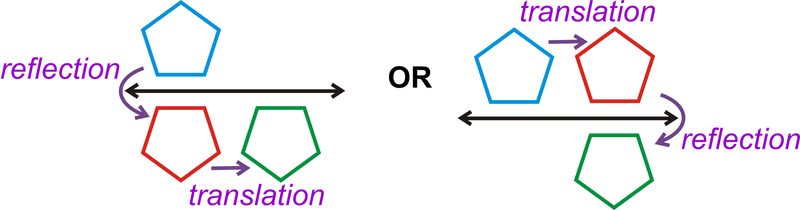
- Una reflexión de deslizamiento es una composición de una reflexión y una traducción. La traslación es en una dirección paralela a la línea de reflexión.
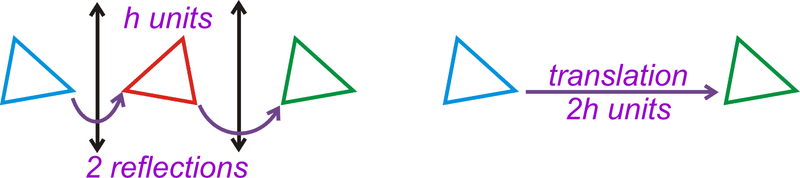
- La composición de dos reflexiones sobre líneas paralelas que están separadas por\(h\) unidades es la misma que una traducción de\(2h\) unidades (Teorema de Reflexiones sobre Líneas Paralelas).
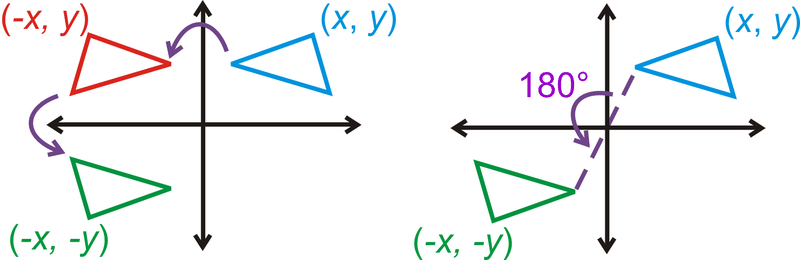
Si compone dos reflexiones sobre cada eje, entonces la imagen final es una rotación de\(180^{\circ}\) alrededor del origen del original (Reflexión sobre el Teorema de los Ejes).
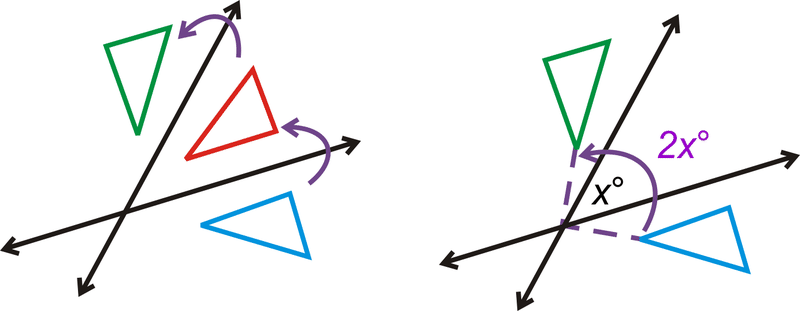
Una composición de dos reflexiones sobre líneas que se cruzan en\(x^{\circ}\) es lo mismo que una rotación de\(2x^{\circ}\). El centro de rotación es el punto de intersección de las dos líneas de reflexión (Teorema de Reflexión sobre Líneas Intersecantes).
¿Y si te dieran las coordenadas de un cuadrilátero y te pidieran reflejar el cuadrilátero y luego traducirlo? ¿Cuáles serían sus nuevas coordenadas?
Ejemplo\(\PageIndex{1}\)
Refleja\(\Delta ABC\) sobre el\(y\) eje y luego traduce la imagen 8 unidades hacia abajo.
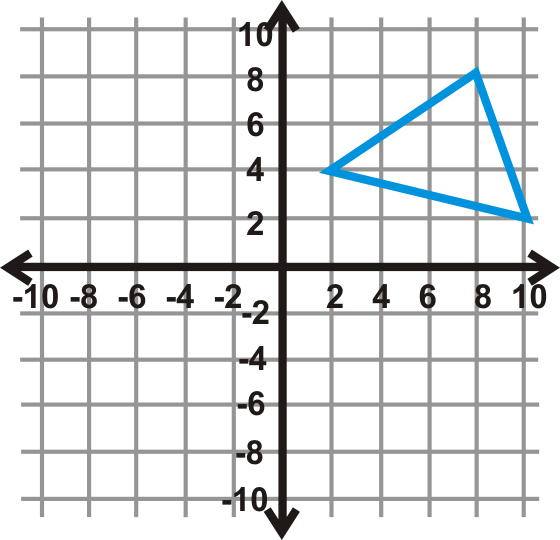
Solución
La imagen verde a la izquierda es la respuesta final.
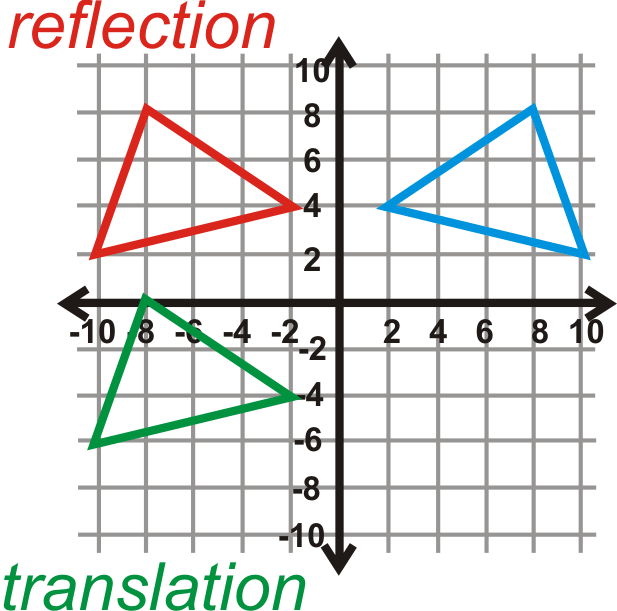
\(\begin{aligned} A(8,8)&\rightarrow A′′(−8,0) \\ B(2,4)&\rightarrow B′′(−2,−4) \\ C(10,2)&\rightarrow C′′(−10,−6) \end{aligned}\)
Ejemplo\(\PageIndex{2}\)
Escribe una sola regla para\(\Delta ABC\) a\(\Delta A′′B′′C′′\) del Ejemplo 1.
Solución
Al observar las coordenadas de\(A\) to\(A′′\), el\(x\) valor −es el signo opuesto y el\(y\) valor −es\(y−8\). Por lo tanto la regla sería\((x,y)\rightarrow (−x,y−8)\).
Ejemplo\(\PageIndex{3}\)
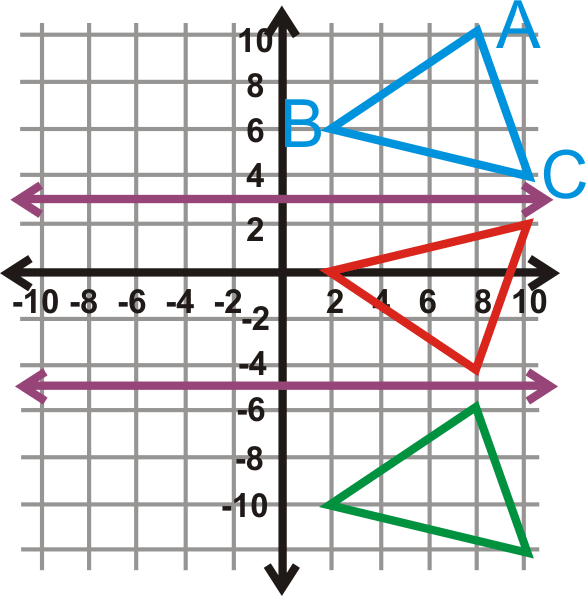
Reflexiona\(\Delta ABC\) sobre\(y=3\) y luego refleja la imagen sobre\(y=−5\).
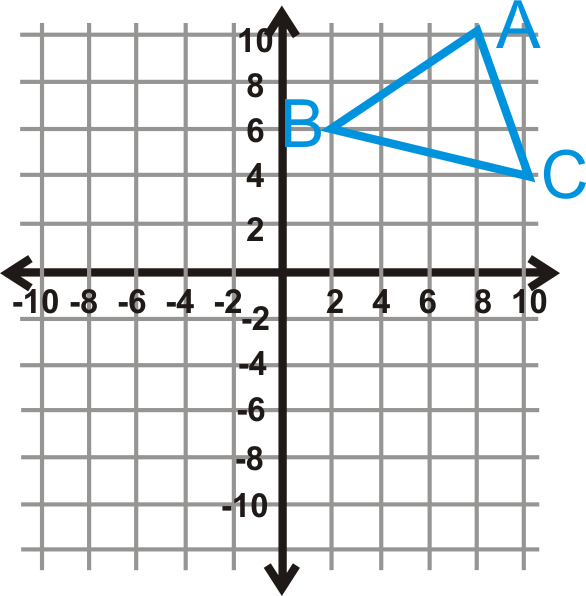
Solución
El orden importa, por lo que\(y=3\) primero reflexionarías sobre, (triángulo rojo) y luego lo reflejarías sobre\(y=−5\) (triángulo verde).
Ejemplo\(\PageIndex{4}\)
Un cuadrado se refleja sobre dos líneas que se cruzan en\(79^{\circ}\) ángulo. ¿A qué transformación será igual esta?
Solución
Del teorema de Reflexión sobre Líneas Intersecantes, esto es lo mismo que una rotación de\(2\cdot 79^{\circ}\) =178^ {\ circ}\).
Ejemplo\(\PageIndex{5}\)
\(\Delta DEF\)tiene vértices\(D(3,−1)\),\(E(8,−3)\), y\(F(6,4)\). Reflexionar\(\Delta DEF\) una\(x=−5\) y otra vez\(x=1\). Determinar cuál de las traducciones sería la misma que esta doble reflexión.
Solución
A partir del Teorema de Reflexiones sobre Líneas Paralelas, sabemos que esta doble reflexión va a ser la misma que una sola traducción de\(2(1−(−5))\) o 12 unidades.
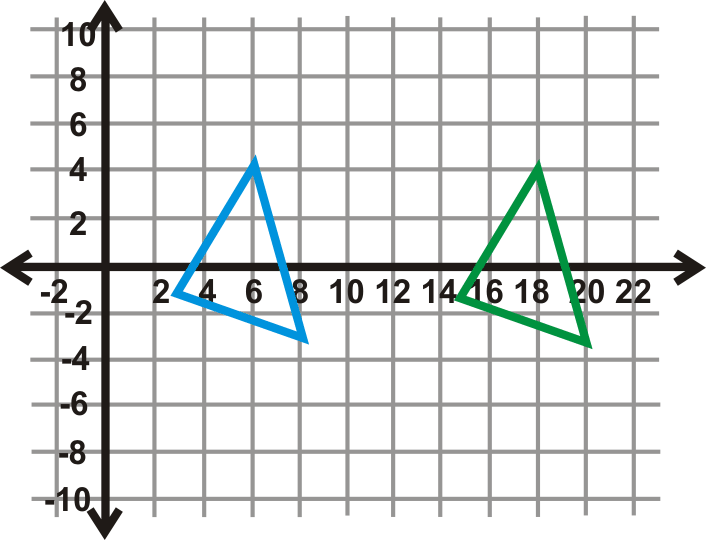
Ejemplo\(\PageIndex{6}\)
Refleja\(\Delta DEF\) desde la Pregunta 2 sobre el\(x\) eje -eje, seguido por el\(y\) -eje. Encuentra las coordenadas de\(\Delta D′′E′′F′′\) y la única transformación que esta doble reflexión es la misma que.
Solución
\(\Delta D′′E′′F′′\)es el triángulo verde en la gráfica a la izquierda. Si comparamos las coordenadas de la misma con\(\Delta DEF\), tenemos:
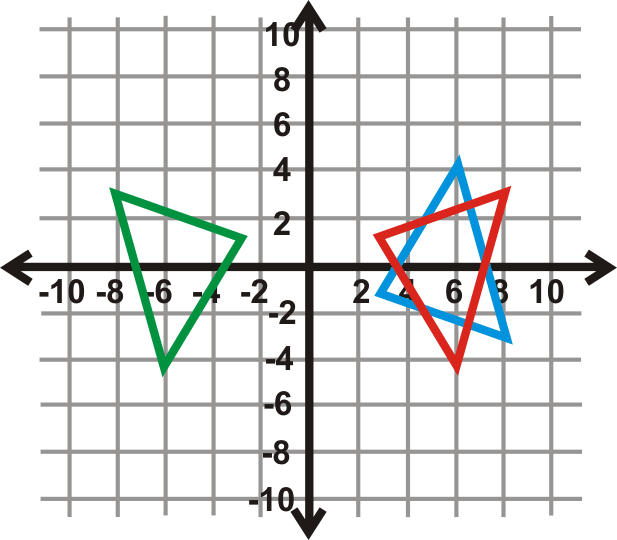
\(\begin{aligned}D(3,−1)&\rightarrow D′′(−3,1) \\ E(8,−3)&\rightarrow E′′(−8,3) \\ F(6,4)&\rightarrow F′′(−6,−4)\end{aligned}\)
Revisar
- Explicar por qué la composición de dos o más isometrías también debe ser una isometría.
- ¿Qué transformación es lo mismo que una reflexión sobre dos líneas paralelas?
- ¿Qué transformación es lo mismo que una reflexión sobre dos líneas que se cruzan?
Utilice la gráfica del cuadrado de la izquierda para responder a las preguntas 4-6.
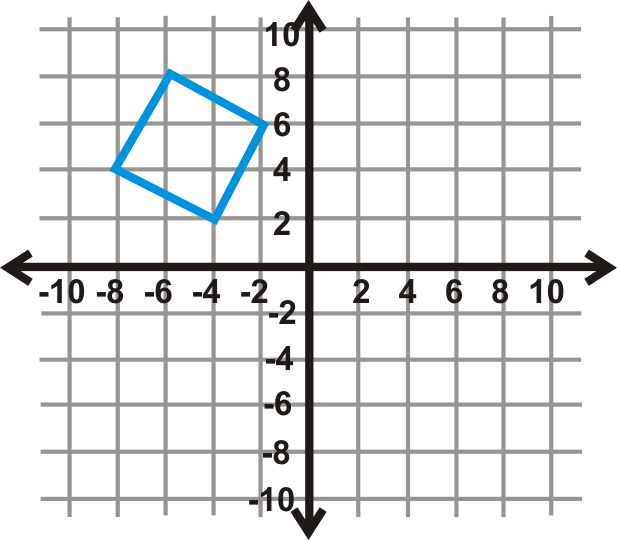
- Realizar una reflexión de deslizamiento sobre el\(x\) eje y hacia la derecha 6 unidades. Escribe las nuevas coordenadas.
- ¿Cuál es la regla para esta reflexión de deslizamiento?
- ¿Qué reflejo de deslizamiento movería la imagen de nuevo a la preimagen?
Utilice la gráfica del cuadrado de la izquierda para responder a las preguntas 7-9.

- Realice una reflexión de deslizamiento hacia la derecha 6 unidades, luego sobre el\(x\) eje. Escribe las nuevas coordenadas.
- ¿Cuál es la regla para esta reflexión de deslizamiento?
- ¿La regla en #8 es diferente a la regla en #5? ¿Por qué o por qué no?
Usa la gráfica del triángulo a la izquierda para responder a las preguntas 10-12.
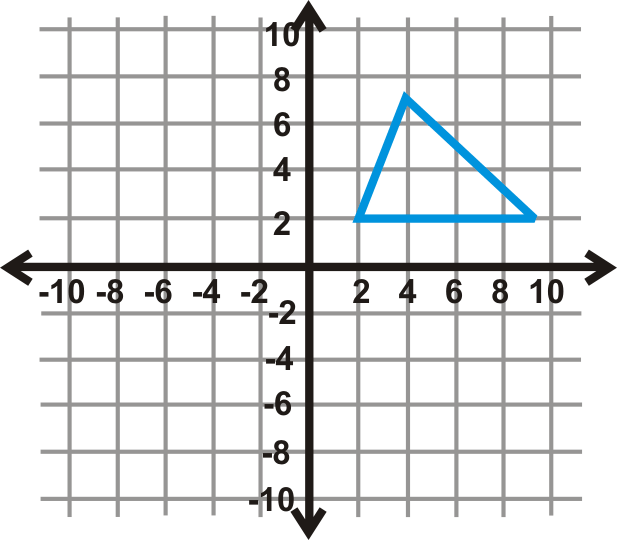
- Realizar una reflexión de deslizamiento sobre el\(y\) eje y hacia abajo 5 unidades. Escribe las nuevas coordenadas.
- ¿Cuál es la regla para esta reflexión de deslizamiento?
- ¿Qué reflejo de deslizamiento movería la imagen de nuevo a la preimagen?
Usa la gráfica del triángulo a la izquierda para responder a las preguntas 13-15.
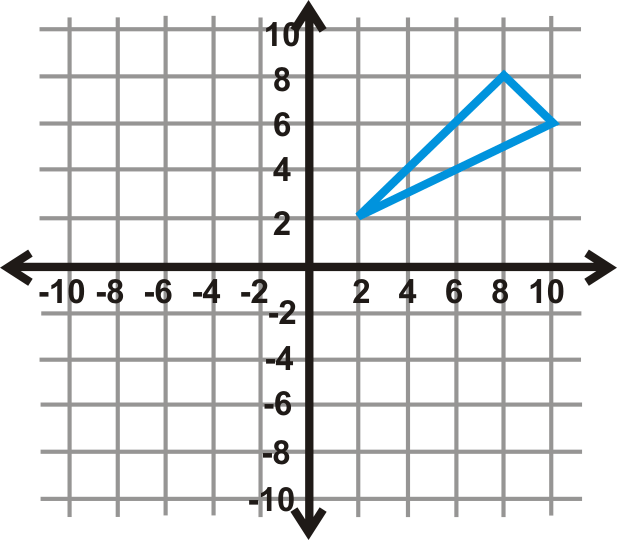
- Reflejar la preimagen sobre\(y=−1\) seguida de\(y=−7\). Dibuja el nuevo triángulo.
- ¿A qué transformación es igual esta doble reflexión?
- Escribe la regla.
Usa la gráfica del triángulo a la izquierda para responder a las preguntas 16-18.

- Reflejar la preimagen sobre\(y=−7\) seguida de\(y=−1\). Dibuja el nuevo triángulo.
- ¿A qué transformación es igual esta doble reflexión?
- Escribe la regla.
- ¿En qué se diferencian los triángulos finales en #13 y #16?
Utilice el trapecio en la gráfica de la izquierda para responder a las preguntas 20-22.
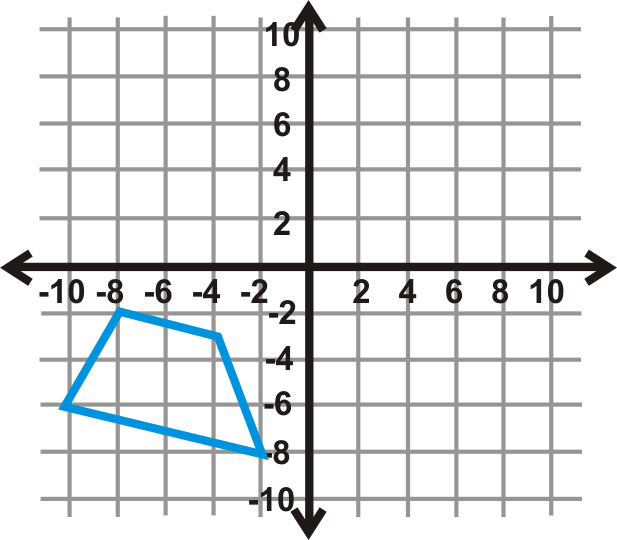
- Refleja la preimagen sobre el\(x\) eje -y luego sobre el\(y\) eje -eje. Dibuja el nuevo trapecio.
- Ahora, empezar de nuevo. Refleja el trapecio sobre el\(y\) eje -y luego sobre el\(x\) eje -eje. Dibuja este trapecio.
- ¿Son diferentes los trapecios finales de #20 y #21? ¿Por qué crees que es eso?
Responde las preguntas que aparecen a continuación. Sé lo más específico que puedas.
- Dos líneas paralelas están separadas por 7 unidades. Si reflejas una figura sobre ambos ¿qué tan lejos estarán con la preimagen y la imagen final?
- Después de una doble reflexión sobre líneas paralelas, una preimagen y su imagen están separadas por 28 unidades. ¿A qué distancia están las líneas paralelas?
- Dos líneas se cruzan en\(165^{\circ}\) ángulo. Si una figura se refleja sobre ambas líneas, ¿a qué distancia estarán la preimagen y la imagen?
- ¿Cuál es el centro de rotación para #25?
- Dos líneas se cruzan en\(83^{\circ}\) ángulo. Si una figura se refleja sobre ambas líneas, ¿a qué distancia estarán la preimagen y la imagen?
- Una preimagen y su imagen están\(244^{\circ}\) separadas. Si la preimagen se reflejaba sobre dos líneas que se cruzaban, ¿en qué ángulo se cruzaban?
- Una preimagen y su imagen están\(98^{\circ}\) separadas. Si la preimagen se reflejaba sobre dos líneas que se cruzaban, ¿en qué ángulo se cruzaban?
- Después de una doble reflexión sobre líneas paralelas, una preimagen y su imagen están separadas 62 unidades. ¿A qué distancia están las líneas paralelas?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 12.6.
El vocabulario
| Término | Definición |
|---|---|
| composición (de transformaciones) | Cuando se realiza más de una transformación sobre una figura. |
| Rotación | Una rotación es una transformación que convierte una figura en el plano de coordenadas un cierto número de grados alrededor de un punto dado sin cambiar la forma o el tamaño de la figura. |
| Reflexión | Una reflexión es una transformación que voltea una figura en el plano de coordenadas a través de una línea dada sin cambiar la forma o el tamaño de la figura. |
| Reflexión de Deslizamiento | Una reflexión seguida de una traslación donde la línea de reflexión es paralela a la dirección de traslación se denomina reflexión de deslizamiento o caminata. |
| Transformación compuesta | Una transformación compuesta, también conocida como composición de transformación, es una serie de múltiples transformaciones realizadas una tras otra. |
Recursos adicionales
Elemento Interactivo
Video: Componer principios de transformaciones - Básicos
Actividades: Composición de las transformaciones Preguntas de discusión
Ayudas de estudio: Guía de estudio de composición de transformaciones
Práctica: Transformaciones compuestas

