8.18: Notación para transformaciones compuestas
- Page ID
- 107592
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Interpretar y usar notación para transformaciones combinadas
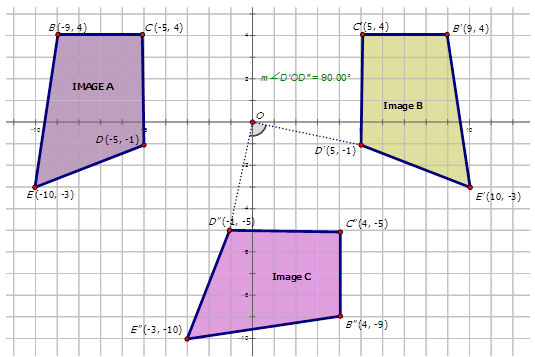
La siguiente figura muestra una transformación compuesta de un trapecio. Escriba la regla de mapeo para la transformación compuesta.
En geometría, una transformación es una operación que mueve, voltea o cambia una forma para crear una nueva forma. Una transformación compuesta es cuando se realizan dos o más transformaciones en una figura (llamada preimagen) para producir una nueva figura (llamada imagen). El orden de las transformaciones realizadas en una transformación compuesta importa.
Para describir una transformación compuesta mediante notación, se indica cada una de las transformaciones que componen la transformación compuesta y las vincula con el símbolo\(\circ\). Las transformaciones se realizan en orden de derecha a izquierda. Recordemos la siguiente notación para traducciones, reflexiones y rotaciones:
- Traducción:\(T_{a,b}: (x,y)\rightarrow (x+a,y+b)\) es una traducción de\(a\) unidades a la derecha y\(b\) unidades arriba.
- Reflexión:\(r_{y−axis}(x,y)\rightarrow (−x,y)\).
- Rotación:\(R_{90^{\circ}}(x,y)=(−y,x)\)
Vamos a graficar la línea que se describe a continuación y la imagen compuesta definida por\(r_{y−axis} \circ R_{90^{\circ}}\):
La primera traducción es un giro de la\(90^{\circ}\) CCW sobre el origen a producir\(X′Y′\). La segunda traslación es una reflexión sobre el\(y\) eje a producir\(X′′Y′′\).
Ahora, graficemos las imágenes compuestas descritas en los siguientes problemas:
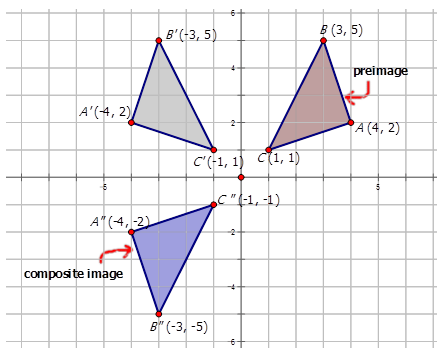
- Imagen A con vértices\(A(3,5)\),\(B(4,2)\) y\(C(1,1)\) se somete a una transformación compuesta con regla de mapeo\(r_{x−axis} \circ r_{y−axis}\).
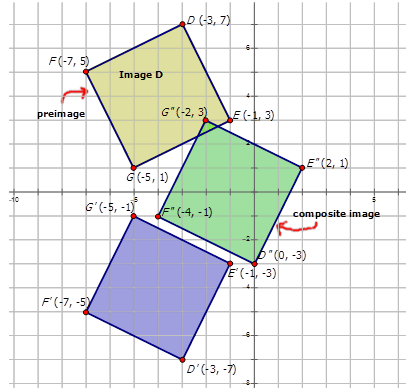
- Imagen\(D\) con vértices\(D(−3,7)\),\(E(−1,3)\),\(F(−7,5)\) y\(G(−5,1)\) se somete a una transformación compuesta con regla de mapeo\(T_{3,4} \circ r_{x−axis}\).
Ejemplo\(\PageIndex{1}\)
Anteriormente, se le pidió que escribiera la regla de mapeo para la siguiente transformación compuesta:

Solución
La transformación de Imagen\(A\) a Imagen\(B\) es un reflejo a través del\(y\) eje. La notación para esto es\(r_{y−axis}\). La transformación de la imagen B para formar imagen\(C\) es una rotación sobre el origen de\(90^{\circ}CW\). La notación para esta transformación es\(R_{270^{\circ}}\). Por lo tanto, la notación para describir la transformación de Imagen\(A\) a Imagen\(C\) es\(R_{270^{\circ}} \circ r_{y−axis}\)
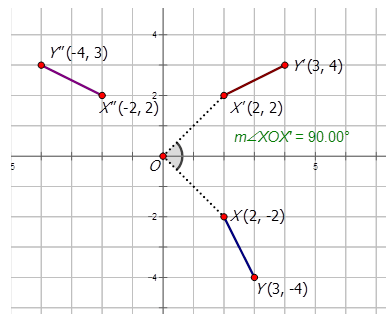
Ejemplo\(\PageIndex{2}\)
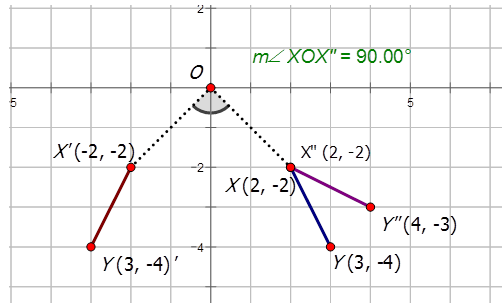
Grafica la línea\(XY\) dado eso\(X(2,−2)\) y\(Y(3,−4)\). También grafica la imagen compuesta que satisface la regla\(R_{90^{\circ}} \circ r_{y−axis}\)
Solución
La primera transformación es una reflexión sobre el\(y\) eje a producir\(X′Y′\). La segunda transformación es un\(90^{\circ}CCW\) giro sobre el origen a producir\(X′′Y′′\).
Ejemplo\(\PageIndex{3}\)
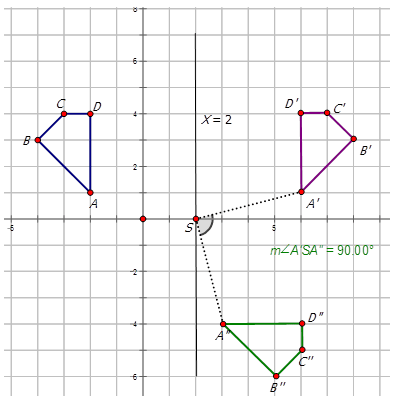
Describa las transformaciones compuestas en el diagrama a continuación y escriba la notación para representar la transformación de figura\(ABCD\) a\(A′′B′′C′′D′′\).
Solución
En el diagrama se muestran dos transformaciones. La primera transformación es una reflexión sobre la línea X=2\) a producir\(A′B′C′D′\). La segunda transformación es una rotación\(90^{\circ}\) CW (o\(270^{\circ}CCW\)) alrededor del punto\((2, 0)\) para producir la figura\(A′′B′′C′′D′′\). La notación para esta transformación compuesta es:
\(R_{270^{\circ}} \circ r_{x=2}\)
Ejemplo\(\PageIndex{4}\)
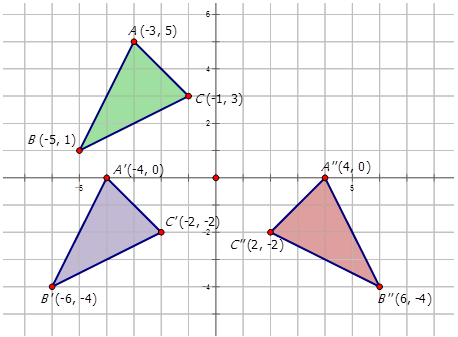
Describa las transformaciones compuestas en el diagrama a continuación y escriba la notación para representar la transformación de figura\(ABC\) a\(A′′B′′C′′\).
Solución
En el diagrama se muestran dos transformaciones. La primera transformación es una traslación de 1 unidad a la izquierda y 5 unidades hacia abajo para producir\(A′B′C′\). La segunda reflexión en el\(y\) eje para producir la figura\(A′′B′′C′′\). La notación para esta transformación compuesta es:
\(r_{y−axis} \circ T_{−1,−5}\)
Revisar
Complete la siguiente tabla:
| Punto de partida | \(T_{3,−4} \circ R_{90^{\circ}}\) | \(r_{x−axis} \circ r_{y−axis}\) | \(T_{1,6} \circ r_{x-axis}\) | \(r_{y−axis} \circ R_{180^{\circ}}\) |
|---|---|---|---|---|
| 1. \((1, 4)\) | \ (T_ {3, −4}\ circ R_ {90^ {\ circ}}\)” class="lt-k12-6155"> | \ (r_ {x−axis}\ circ r_ {y−axis}\)” class="lt-k12-6155"> | \ (T_ {1,6}\ circ r_ {eje x}\)” class="lt-k12-6155"> | \ (r_ {y−axis}\ circ R_ {180^ {\ circ}}\)” class="lt-k12-6155"> |
| 2. \((4, 2)\) | \ (T_ {3, −4}\ circ R_ {90^ {\ circ}}\)” class="lt-k12-6155"> | \ (r_ {x−axis}\ circ r_ {y−axis}\)” class="lt-k12-6155"> | \ (T_ {1,6}\ circ r_ {eje x}\)” class="lt-k12-6155"> | \ (r_ {y−axis}\ circ R_ {180^ {\ circ}}\)” class="lt-k12-6155"> |
| 3. \((2, 0)\) | \ (T_ {3, −4}\ circ R_ {90^ {\ circ}}\)” class="lt-k12-6155"> | \ (r_ {x−axis}\ circ r_ {y−axis}\)” class="lt-k12-6155"> | \ (T_ {1,6}\ circ r_ {eje x}\)” class="lt-k12-6155"> | \ (r_ {y−axis}\ circ R_ {180^ {\ circ}}\)” class="lt-k12-6155"> |
| 4. \((-1, 2)\) | \ (T_ {3, −4}\ circ R_ {90^ {\ circ}}\)” class="lt-k12-6155"> | \ (r_ {x−axis}\ circ r_ {y−axis}\)” class="lt-k12-6155"> | \ (T_ {1,6}\ circ r_ {eje x}\)” class="lt-k12-6155"> | \ (r_ {y−axis}\ circ R_ {180^ {\ circ}}\)” class="lt-k12-6155"> |
| 5. \((-2, -3)\) | \ (T_ {3, −4}\ circ R_ {90^ {\ circ}}\)” class="lt-k12-6155"> | \ (r_ {x−axis}\ circ r_ {y−axis}\)” class="lt-k12-6155"> | \ (T_ {1,6}\ circ r_ {eje x}\)” class="lt-k12-6155"> | \ (r_ {y−axis}\ circ R_ {180^ {\ circ}}\)” class="lt-k12-6155"> |
| 6. \((4, -1)\) | \ (T_ {3, −4}\ circ R_ {90^ {\ circ}}\)” class="lt-k12-6155"> | \ (r_ {x−axis}\ circ r_ {y−axis}\)” class="lt-k12-6155"> | \ (T_ {1,6}\ circ r_ {eje x}\)” class="lt-k12-6155"> | \ (r_ {y−axis}\ circ R_ {180^ {\ circ}}\)” class="lt-k12-6155"> |
| 7. \((3, -2)\) | \ (T_ {3, −4}\ circ R_ {90^ {\ circ}}\)” class="lt-k12-6155"> | \ (r_ {x−axis}\ circ r_ {y−axis}\)” class="lt-k12-6155"> | \ (T_ {1,6}\ circ r_ {eje x}\)” class="lt-k12-6155"> | \ (r_ {y−axis}\ circ R_ {180^ {\ circ}}\)” class="lt-k12-6155"> |
| 8. \((5, 4)\) | \ (T_ {3, −4}\ circ R_ {90^ {\ circ}}\)” class="lt-k12-6155"> | \ (r_ {x−axis}\ circ r_ {y−axis}\)” class="lt-k12-6155"> | \ (T_ {1,6}\ circ r_ {eje x}\)” class="lt-k12-6155"> | \ (r_ {y−axis}\ circ R_ {180^ {\ circ}}\)” class="lt-k12-6155"> |
| 9. \((-3, 7)\) | \ (T_ {3, −4}\ circ R_ {90^ {\ circ}}\)” class="lt-k12-6155"> | \ (r_ {x−axis}\ circ r_ {y−axis}\)” class="lt-k12-6155"> | \ (T_ {1,6}\ circ r_ {eje x}\)” class="lt-k12-6155"> | \ (r_ {y−axis}\ circ R_ {180^ {\ circ}}\)” class="lt-k12-6155"> |
| 10. \((0, 0)\) | \ (T_ {3, −4}\ circ R_ {90^ {\ circ}}\)” class="lt-k12-6155"> | \ (r_ {x−axis}\ circ r_ {y−axis}\)” class="lt-k12-6155"> | \ (T_ {1,6}\ circ r_ {eje x}\)” class="lt-k12-6155"> | \ (r_ {y−axis}\ circ R_ {180^ {\ circ}}\)” class="lt-k12-6155"> |
Escribe la notación que representa la transformación compuesta de la preimagen\(A\) a las imágenes compuestas en los diagramas a continuación.
-
Figura\(\PageIndex{9}\) -
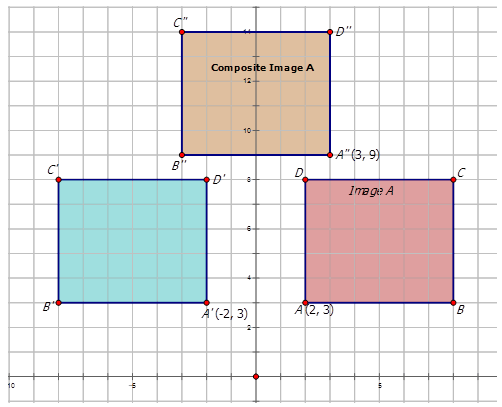
Figura\(\PageIndex{10}\) -
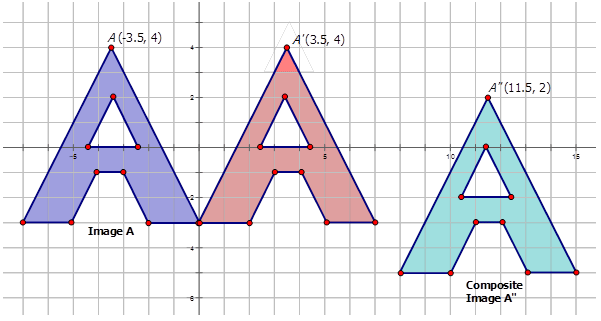
Figura\(\PageIndex{11}\) -
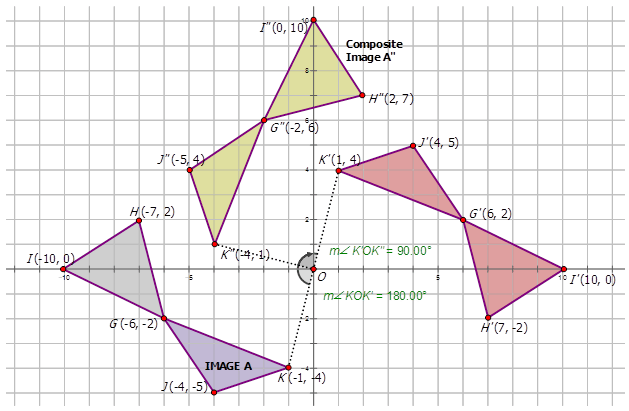
Figura\(\PageIndex{12}\) -
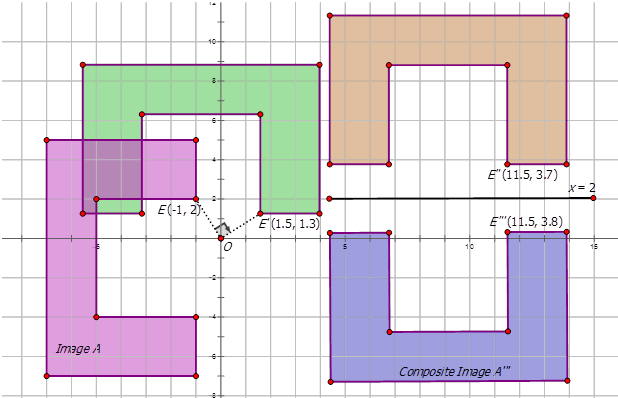
Figura\(\PageIndex{13}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.15.
El vocabulario
| Término | Definición |
|---|---|
| Reflexiones | Las reflexiones son transformaciones que dan como resultado una “imagen especular” de una función padre. Son causadas por signos diferentes entre las funciones padre e hijo. |
| Rotación | Una rotación es una transformación que convierte una figura en el plano de coordenadas un cierto número de grados alrededor de un punto dado sin cambiar la forma o el tamaño de la figura. |
| Transformación | Una transformación mueve una figura de alguna manera en el plano de coordenadas. |
Recursos adicionales
Práctica: Notación para transformaciones compuestas

