9.3: Secciones transversales y redes
- Page ID
- 107289
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Las secciones transversales son intersecciones de un plano con un sólido. Las redes son representaciones desplegadas y planas de los lados de una forma 3D que permiten encontrar la suma del área de las caras mostrando los bordes y las caras en 2-D.
Si bien nuestro mundo es tridimensional, estamos acostumbrados a modelar y pensar en objetos tridimensionales sobre papel (en dos dimensiones). Hay algunas formas comunes de ayudar a pensar en tres dimensiones en dos dimensiones. Una forma de “ver” una figura tridimensional en un plano bidimensional (como en una hoja de papel o una pantalla de computadora) es usar secciones transversales. Otra forma de “ver” una figura tridimensional en un plano bidimensional es usar una red.
Sección transversal: La intersección de un plano con un sólido.
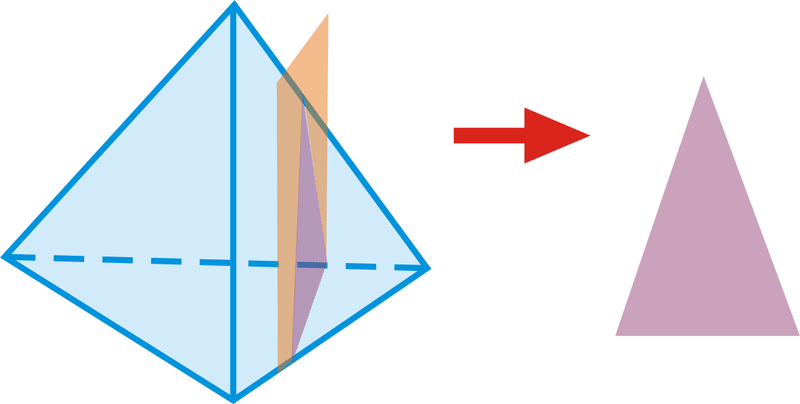
La sección transversal del plano del durazno y el tetraedro es un triángulo.
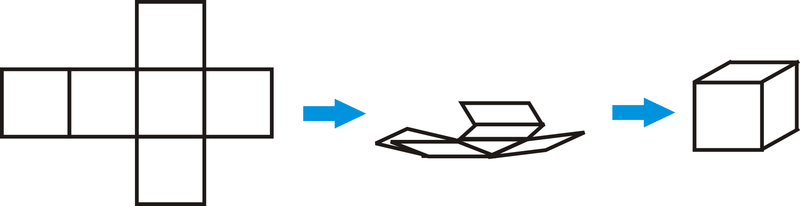
Red: Una representación desplegada y plana de los lados de una forma tridimensional.
Es bueno poder visualizar secciones transversales y redes como los objetos tridimensionales que representan.
¿Y si te dieran una figura tridimensional como una pirámide y quisieras saber cómo sería esa figura en dos dimensiones? ¿Cómo sería una rebanada plana o una representación plana desplegada de ese sólido?
Ejemplo\(\PageIndex{1}\)
Describir la sección transversal formada por la intersección del plano y el sólido.
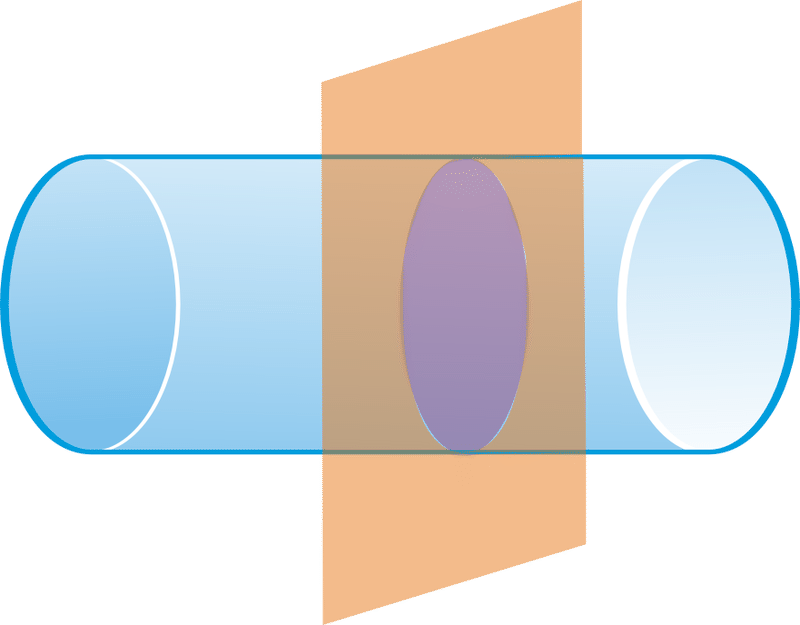
Solución
Círculo
Ejemplo\(\PageIndex{2}\)
Determinar qué forma está formada por la siguiente red.
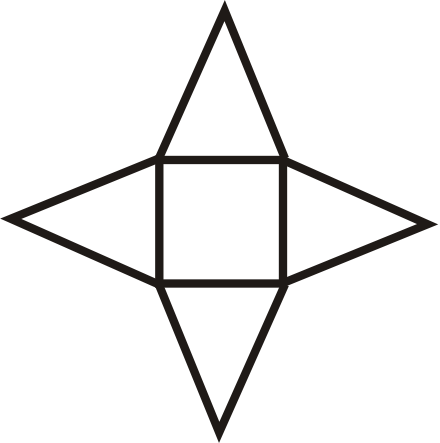
Solución
Pirámide cuadrada
Ejemplo\(\PageIndex{3}\)
¿Cuál es la forma que forma la intersección del plano y el octaedro regular?
-
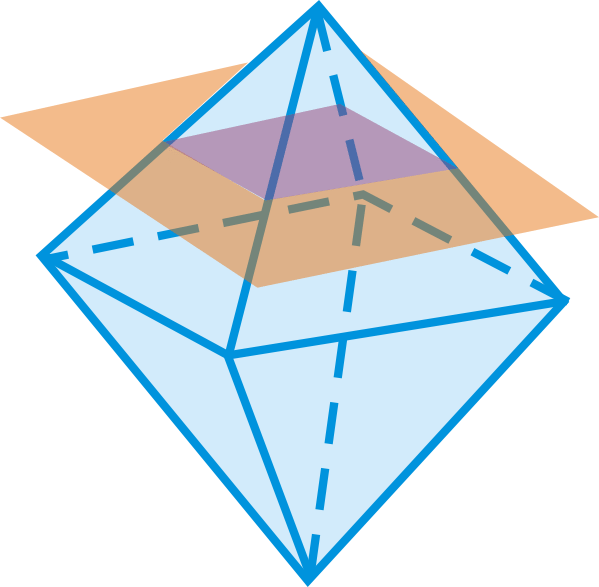
Figura\(\PageIndex{5}\) -
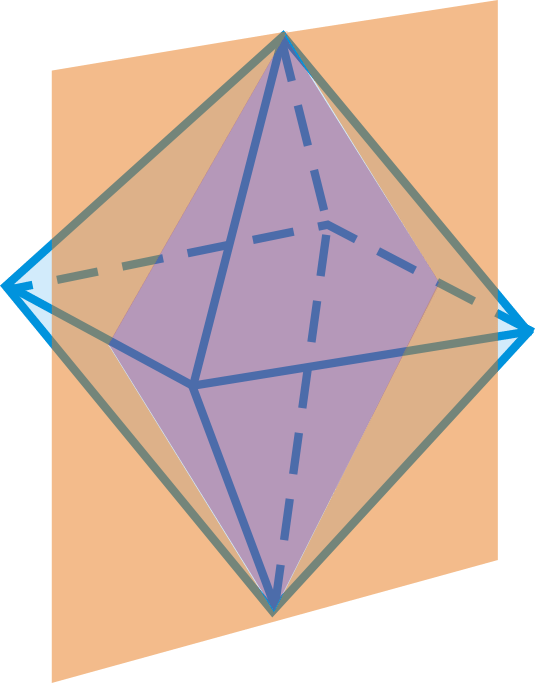
Figura\(\PageIndex{6}\) -
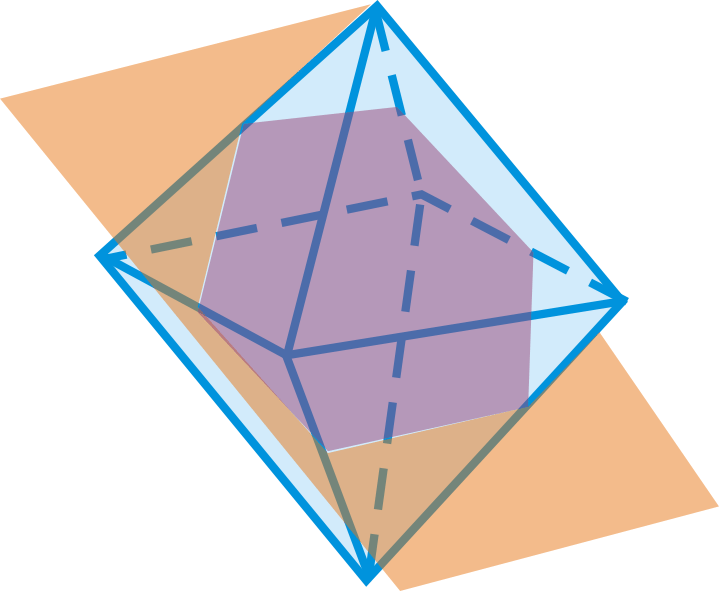
Figura\ (\ pageIndex {7}\
Solución
- Cuadrado
- Rombo
- Hexágono
Ejemplo\(\PageIndex{4}\)
¿Qué tipo de figura crea esta red?
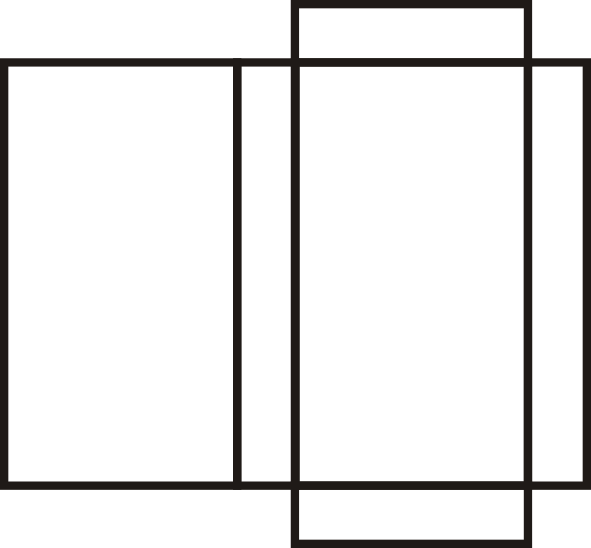
Solución
La red crea un prisma rectangular.
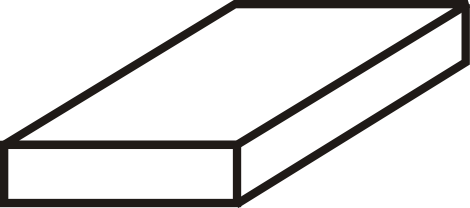
Ejemplo\(\PageIndex{5}\)
Dibuja una red del prisma triangular derecho debajo.
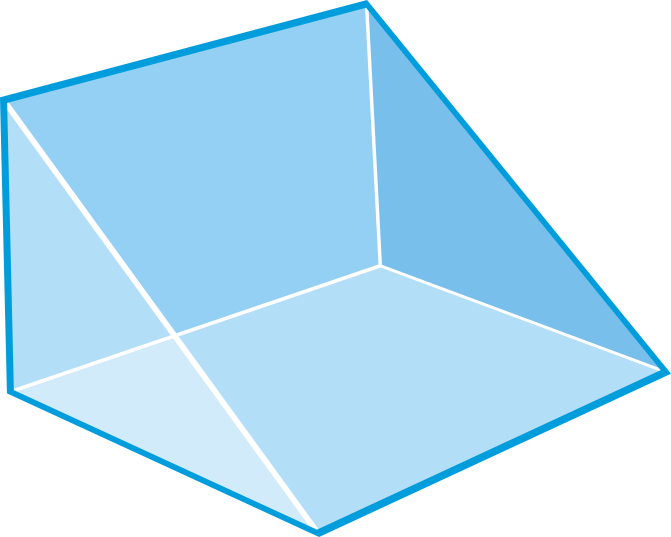
Solución
La red tendrá dos triángulos y tres rectángulos. Los rectángulos son de diferentes tamaños y los dos triángulos son iguales.
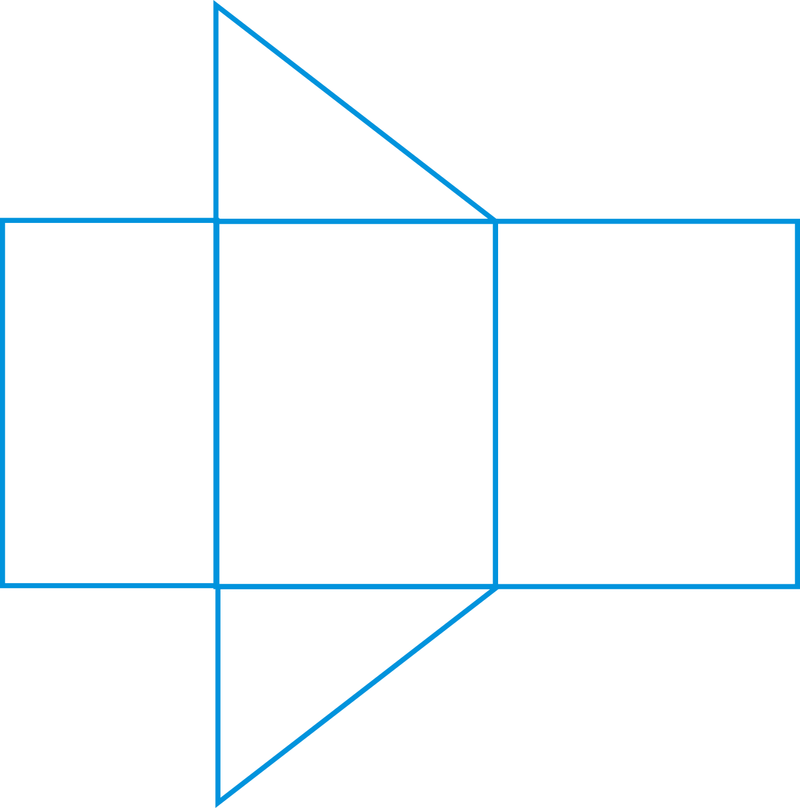
Hay varias redes diferentes de cualquier poliedro. Por ejemplo, esta red podría tener los triángulos en cualquier lugar a lo largo de la parte superior o inferior de los tres rectángulos.
Revisar
Describir la sección transversal formada por la intersección del plano y el sólido.
-
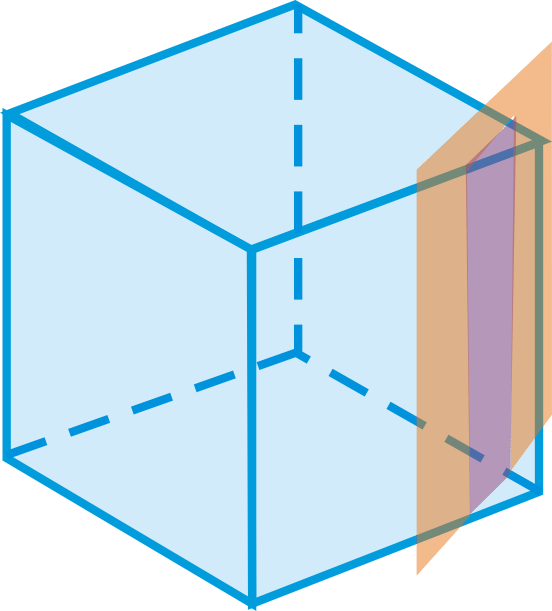
Figura\(\PageIndex{12}\) -
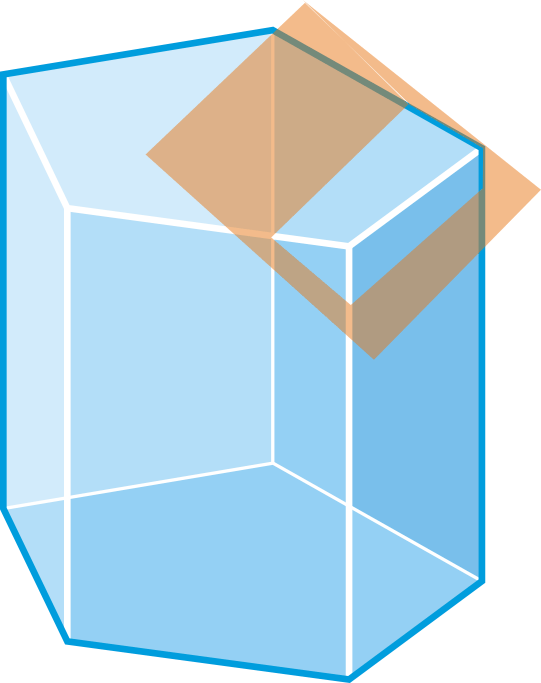
Figura\(\PageIndex{13}\)
Dibuje la red para los siguientes sólidos.
-
Figura\(\PageIndex{14}\) -
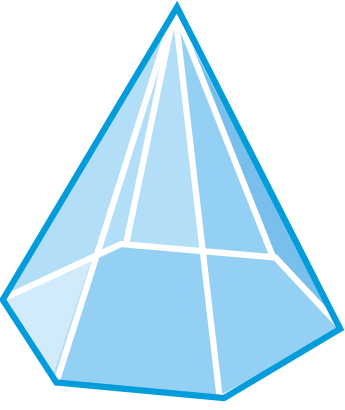
Figura\(\PageIndex{15}\) -
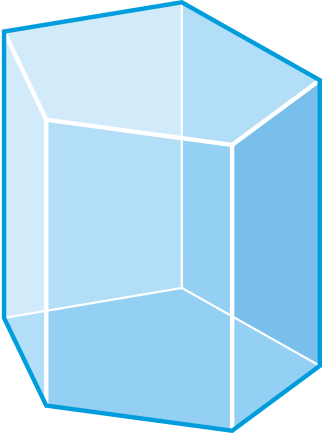
Figura\(\PageIndex{16}\) -
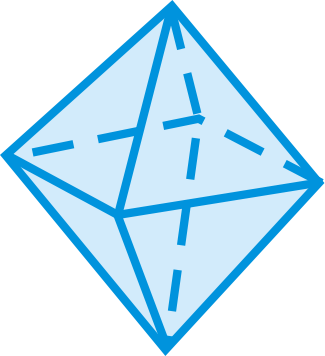
Figura\(\PageIndex{17}\) -
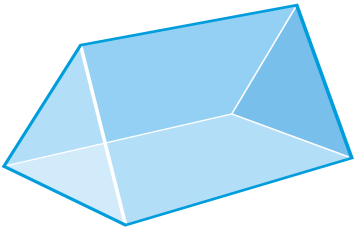
Figura\(\PageIndex{18}\) -
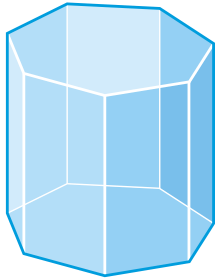
Figura\(\PageIndex{19}\)
Determinar qué forma está formada por las siguientes redes.
-
Figura\(\PageIndex{20}\) -
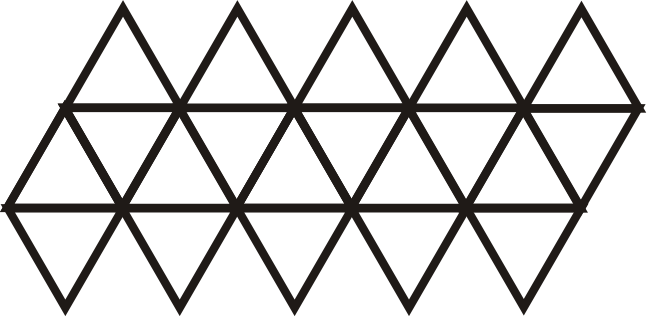
Figura\(\PageIndex{21}\) -
Figura\(\PageIndex{22}\) -
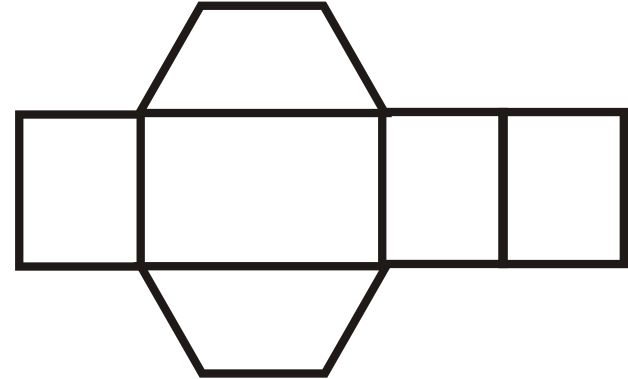
Figura\ (\ pageIndex {23}\
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.2.
El vocabulario
| Término | Definición |
|---|---|
| sección transversal | La intersección de un plano con un sólido. |
| neto | Una representación desplegada y plana de los lados de una forma tridimensional. |
| sección transversal | Una sección transversal es la intersección de un sólido tridimensional con un plano. |
| Poliedro | Un poliedro es un sólido sin curvas, superficies o aristas. Todas las caras son polígonos y todas las aristas son segmentos de línea. |
| Volumen | El volumen es la cantidad de espacio dentro de los límites de un objeto tridimensional. |