9.13: Volumen de Prismas Usando Cubos Unitarios
- Page ID
- 107329
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Usa cubos para encontrar el volumen de un prisma.

La tarea de Jerry en su clase de carpintería es construir un contenedor de almacenamiento de madera que contendrá al menos 48 unidades cúbicas de material. Jerry ya comenzó en el contenedor rectangular, que es de 4 unidades de ancho y 2 unidades de largo. Jerry no está seguro de qué altura debe tener el contenedor para poder contener un volumen de 48 unidades cúbicas. ¿Cómo puede Jerry usar esta información para determinar la altura del contenedor?
En este concepto, aprenderás a identificar el volumen de prismas usando cubos unitarios.
Encontrar el volumen de prismas usando cubos unitarios
Volumen es la cantidad de espacio dentro de una figura sólida.

Estos cubos conforman un prisma rectangular. Los cubos representan el volumen del prisma. Este prisma es de cinco cubos por dos cubos por un cubo. Es decir, tiene cinco cubos de largo, por dos cubos de alto por un cubo de ancho. Se puede multiplicar cada uno de estos valores juntos para obtener el volumen del prisma rectangular.
\(5\times 2\times 1=10\text{ cubic units }\)
El volumen del prisma rectangular es de 10 unidades cúbicas o\(\text{ units}^{3}\). Las unidades son unidades cúbicas porque multiplicaste las unidades 3 veces cuando multiplicaste la altura, la longitud y la anchura.
Aquí hay otro prisma.
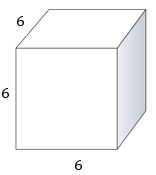
Primero, para averiguar el volumen de este prisma, identificar las mediciones.
Largo - 6
Ancho - 6
Altura - 6
A continuación, sustituya estos valores en la fórmula por volumen luego resuelva.
\(\text{Length }\times \text{ Width }\times \text{ Height}=\text{ Volume in cubic units}\)
\(6\times 6\times 6=216\text{ cubic units}\)
El volumen del cubo es\(216\text{ cubic units}\).
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Jerry y el contenedor de almacenamiento que está construyendo.
El contenedor tiene 4 unidades de ancho y 2 unidades de largo cuando se enteró del requerimiento de volumen. El contenedor necesita tener un volumen de 48 unidades cúbicas. ¿Cómo puede Jerry usar esta información para determinar la altura que debe tener el contenedor?
Solución
Primero, para calcular la altura que debe tener el contenedor, identifique las medidas dadas.
Largo - 2 unidades
Ancho - 4 unidades
Altura -?
Volumen - 48 unidades cúbicas
A continuación, sustituya estos valores en la fórmula para volumen.
\(\begin{aligned} \text{ Length }\times \text{ Width} \times \text{ Height}&=Volume in cubic units \\ 2\times 4\times H&=48 \text{ cubic units}\end{aligned}\)
Entonces, multiplicar.
\(8(H)=48\)
Después, divida ambos lados por 8.
\(H=6\text{ units}\)
El contenedor debe tener una altura de 6 unidades.
Ejemplo\(\PageIndex{2}\)
¿Cuál es el volumen de esta cifra?

Solución
Primero, para averiguar el volumen de este prisma, identificar las mediciones.
Largo - 4 unidades
Ancho - 4 unidades
Altura - 3 unidades
A continuación, sustituya estos valores en la fórmula para volumen luego resuelva.
\(\begin{aligned} \text{ Length}\times \text{ Width}\times \text{ Height}=\text{ Volume in cubic units} \\ 4\times 4\times 3=216 \text{ cubic units}\end{aligned}\)
El volumen del prisma es\(48\text{ cubic units}\), o\(48 \text{ units}^{3}\).
Ejemplo\(\PageIndex{3}\)
Encuentra el volumen del prisma.

Solución
Primero, para averiguar el volumen de este prisma, identificar las mediciones.
Largo - 1
Ancho - 2
Altura - 5
A continuación, sustituya estos valores en la fórmula para volumen luego resuelva.
\(\begin{aligned} \text{Length}\times \text{ Width}\times \text{Height}&=\text{Volume in cubic units} \\ 1\times 2\times 5&=10 \text{ cubic units}\end{aligned}\)
El volumen del prisma es de 10 unidades cúbicas.
Ejemplo\(\PageIndex{4}\)
Encuentra el volumen del prisma.
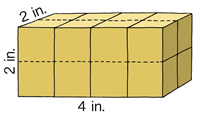
Solución
Primero, para averiguar el volumen de este prisma, identificar las mediciones.
Largo - 2 pulgadas
Ancho - 4 pulgadas
Altura - 2 pulgadas
A continuación, sustituya estos valores en la fórmula para volumen luego resuelva.
\(\begin{aligned} \text{Length}\times \text{Width}\times \text{Height}&=\text{ Volume in cubic units}\\ 2\times 4\times 2&=16 \text{ cubic inches}\end{aligned}\)
El volumen del cubo es de 16 pulgadas cúbicas.
Ejemplo\(\PageIndex{5}\)
Encuentra el volumen del prisma.
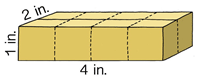
Solución
Primero, para averiguar el volumen de este prisma, identificar las mediciones.
Largo - 2 pulgadas
Ancho - 4 pulgadas
Altura - 1 pulgada
A continuación, sustituya estos valores en la fórmula para volumen luego resuelva.
\(\begin{aligned} \text{Length}\times \text{Width}\times \text{Height}&=\text{ Volume in cubic units}\\ 2\times 4\times 1&=8 \text{ cubic units}\end{aligned}\)
El volumen del prisma es de 8 pulgadas cúbicas.
Revisar
Encuentra el volumen de cada prisma.
-
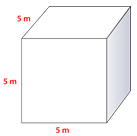
Figura\(\PageIndex{8}\) -

Figura\(\PageIndex{9}\) -

Figura\(\PageIndex{10}\) -
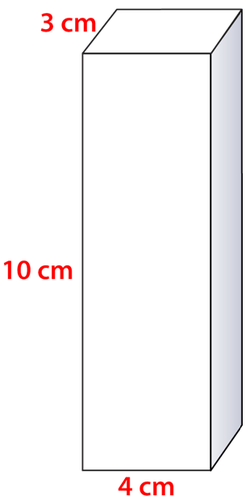
Figura\(\PageIndex{11}\) -
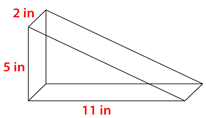
Figura\(\PageIndex{12}\) -

Figura\(\PageIndex{13}\) -

Figura\(\PageIndex{14}\) -

Figura\(\PageIndex{15}\) -

Figura\(\PageIndex{16}\) -

Figura\(\PageIndex{17}\)
Identificar cada tipo de prisma.
-

Figura\(\PageIndex{18}\) -

Figura\(\PageIndex{19}\) -

Figura\(\PageIndex{20}\) -

Figura\(\PageIndex{21}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.15.
vocabulario
| Término | Definición |
|---|---|
| Net | Una red es un diagrama que muestra una vista “aplanada” de un sólido. En una red, cada cara y base se muestra con todas sus dimensiones. Una red también puede servir como patrón para construir un sólido tridimensional. |
| Prisma Rectangular | Un prisma rectangular es un prisma compuesto por dos bases rectangulares y cuatro caras rectangulares. |
| Superficie | El área superficial es el área total de todas las superficies de un objeto tridimensional. |
| Prisma Triangular | Un prisma triangular es un prisma compuesto por dos bases triangulares y tres caras rectangulares. |
| Volumen | El volumen es la cantidad de espacio dentro de los límites de un objeto tridimensional. |
Recursos adicionales
Video: Volumen de Geometría Sólida
Práctica: Volumen de prismas usando cubos unitarios

