9.12: Volumen de Prismas
- Page ID
- 107347
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Usa la fórmula\(V = Bh\)

Karen y Lance están construyendo un patio trasero para sus dos hijos. Tienen un columpio, un tiovivo y una caja de arena ya instalada. Lance va a la tienda a comprar arena para el arenero y necesita saber cuánta arena puede contener. La caja de arena mide 6 pies de ancho, 8 pies de largo y 1 pie de profundidad. ¿Cómo puede Lance usar una fórmula para calcular el volumen total de este sandbox?
En este concepto, aprenderás a encontrar volúmenes de prismas rectangulares y triangulares utilizando fórmulas.
Encontrar el volumen de prismas
Volumen es la cantidad de espacio dentro de una figura sólida.
Llenar figuras sólidas con cubos es una forma sencilla y fácil de entender el volumen. Si puedes contar los cubos, puedes averiguar el volumen. Sin embargo, a veces tendrás que averiguar el volumen de un prisma cuando no hay cubos dibujados dentro de él.
Echa un vistazo al prisma de abajo.
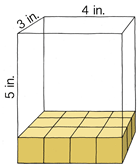
Este prisma rectangular tiene una altura de 5 pulgadas, un ancho de 3 pulgadas y una longitud de 4 pulgadas.
Aquí hay una fórmula para encontrar el volumen de este tipo prisma.
\(V=Bh\)
B significa el área de la base, que es la longitud por el ancho, y h significa la altura.
Entonces, primero averiguar el área de la base.
\(A=3\times 4=12\)
A continuación, multiplicar\(B\) por\(h\).
\(\begin{aligned} h&=5\\ V&=12\times 5=60\end{aligned}\)
El volumen es de 60 pulgadas cúbicas o\(in^{3}\). Recuerda, el volumen está en unidades cúbicas.
Veamos otro ejemplo. Encuentra el volumen usando la fórmula de volumen.
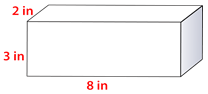
\(V=Bh\)
Primero, figura el área de la base.
El área de la base es\(2\times 8=16\)
A continuación, multiplique la B por h. La altura es de 3 pulgadas.
\(\begin{aligned} V&=16\times 3 \\ V&=48\: \text{ in}^{3}\end{aligned}\)
El volumen de este prisma rectangular es\(48\:\text{ in}^{3}\).
Se puede utilizar la misma fórmula para encontrar el volumen del prisma triangular. Excepto esta vez, el área de la base es un triángulo y no un rectángulo.
Echa un vistazo al prisma triangular de abajo.

Para encontrar el volumen de un prisma triangular, multiplique el área de la base (\(B\)) con la altura del prisma.
\(V=Bh\)
Primero, encuentra el área de la base triangular usando la fórmula para el área de un triángulo.
\(\begin{aligned} A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(15\times 6) \\ A&=\dfrac{1}{2}(90) \\ A&=45\:\text{ sq. units}\end{aligned}\)
A continuación, multiplica esto por la altura.
\(\begin{aligned} V&=Bh \\ V&=(45)h \\ V&=45(2) \\ V&=90\text{ cubic centimeters} or \text{ cm}^{3}\end{aligned}\)
El volumen del prisma es\(90\text{ cm}^{3}\).
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre la caja de arena de Lance y Karen.
La caja de arena mide 6 pies de ancho, 8 pies de largo y 1 pie de profundidad. Lance necesita conocer el volumen.
Solución
Para encontrar el volumen de la caja de arena, que es un prisma con una de sus bases quitadas, utilice la siguiente fórmula.
\(V=Bh\)
Primero, sustituir en los valores dados. Recuerda, B es largo por ancho.
\(\begin{aligned} V&=(8\times 6)(1)\\ V&=48\text{ ft}^{3}\end{aligned}\)
Este es el volumen total.
A continuación, para saber cuánta arena necesita para llenar la caja de arena a mitad de camino, divida el volumen total por 2.
\(48\divide 2=24\)
Lance necesita 24 pies cúbicos de arena para llenar la caja de arena hasta la mitad.
Ejemplo\(\PageIndex{2}\)
Encuentra el volumen del prisma.
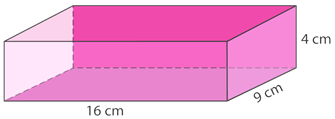
Solución
Para encontrar el volumen de un prisma, utilice la siguiente fórmula.
\(V=Bh\)
Primero, sustituir en los valores dados. Recuerda que B es largo por ancho.
\(\begin{aligned} V&=(16\times 9)(4) \\ V&=576\text{ cm}^{3}\end{aligned}\)
La respuesta es\(576\text{ cm}^{3}\).
Ejemplo\(\PageIndex{3}\)
Encuentra el volumen del prisma.

Solución
Primero, para encontrar el volumen de un prisma, usa la siguiente fórmula.
\(V=Bh\)
A continuación, sustituir en los valores dados. Recuerda que B es largo por ancho. Se trata de un cubo cuadrado, por lo que la longitud, la anchura y la altura son las mismas.
\(\begin{aligned} V&=(5\times 5)(5) \\V&=125\text{ in}^{3}\end{aligned}\)
La respuesta es\(125\text{ in}^{3}\).
Ejemplo\(\PageIndex{4}\)
Encuentra el volumen del prisma.
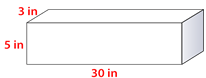
Solución
Primero, para encontrar el volumen de un prisma, usa la siguiente fórmula.
\(V=Bh\)
Primero, sustituir en los valores dados. Recuerda, B es largo por ancho.
\(\begin{aligned} V&=(30\times 5)(3) \\ V&=450\text{ in}^{3}\end{aligned}\)
La respuesta es\(450\text{ in}^{3}\).
Ejemplo\(\PageIndex{5}\)
Encuentra el volumen del prisma.
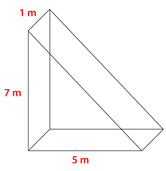
Solución
Para encontrar el volumen de un prisma triangular, multiplique el área de la base (B) con la altura del prisma.
\(V=Bh\)
Primero, encuentra el área de la base triangular usando la fórmula para el área de un triángulo.
\(\begin{aligned} A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(5\times 7) \\ A&=\dfrac{1}{2}(35) \\ A&=17.5 \text{ sq. m} \end{aligned}\)
A continuación, multiplica esto por la altura.
\(\begin{aligned} V&=Bh \\ V&=(17.5)1 \\ V&=17.5\text{ cm}^{3}\end{aligned}\)
El volumen del prisma es\(17.5\text{ cm}^{3}\).
Revisar
Encuentra el volumen de cada prisma rectangular. Recuerda etiquetar tu respuesta en unidades cúbicas.
- Largo = 5 in, ancho = 3 in, alto = 4 in
- Largo = 7 m, ancho = 6 m, alto = 5 m
- Largo = 8 cm, ancho = 4 cm, alto = 9 cm
- Largo = 8 cm, ancho = 4 cm, alto = 12 cm
- Largo = 10 pies, ancho = 5 pies, alto = 6 pies
- Largo = 9 m, ancho = 8 m, alto = 11 m
- Largo = 5.5 in, ancho = 3 in, alto = 5 in
- Largo = 6.6 cm, ancho = 5 cm, alto = 7 cm
- Largo = 7 pies, ancho = 4 pies, alto = 6 pies
- Largo = 15 m, ancho = 8 m, alto = 10 m
Encuentra el volumen de cada prisma triangular. Recuerda que h\) significa la altura de la base triangular y H\) significa la altura de todo el prisma.
- \(b=6\text{ in}\),\(h=4\text{ in}\),\(H=5\text{ in}\)
- \(b=7\text{ in}\),\(h=5\text{ in}\),\(H=9\text{ in}\)
- \(b=10\text{ m}\),\(h=8\text{ m}\),\(H=9\text{ m}\)
- \(b=12\text{ m}\),\(h=10\text{ m}\),\(H=13\text{ m}\)
- \(b=8\text{ cm}\),\(h=6\text{ cm}\),\(H=9\text{ cm}\)
Responder verdadero o falso para cada una de las siguientes preguntas.
- El volumen es la cantidad de espacio que una figura puede contener en su interior.
- El volumen de un prisma rectangular es siempre mayor que el volumen de un cubo.
- El volumen de un prisma triangular es menor que un prisma rectangular con la base del mismo tamaño.
- Un pintor necesitaría conocer la superficie de una casa para hacer su trabajo correctamente.
- Si Marcus está cubriendo su libro con una portada de libro, Marcus está cubriendo la superficie del libro.
vocabulario
| Término | Definición |
|---|---|
| Net | Una red es un diagrama que muestra una vista “aplanada” de un sólido. En una red, cada cara y base se muestra con todas sus dimensiones. Una red también puede servir como patrón para construir un sólido tridimensional. |
| Prisma Rectangular | Un prisma rectangular es un prisma compuesto por dos bases rectangulares y cuatro caras rectangulares. |
| Superficie | El área superficial es el área total de todas las superficies de un objeto tridimensional. |
| Prisma Triangular | Un prisma triangular es un prisma compuesto por dos bases triangulares y tres caras rectangulares. |
Recursos adicionales
Elemento Interactivo
Video: Volumen de Geometría Sólida
Práctica: Volumen de prismas

