9.23: Superficie de Conos
- Page ID
- 107311
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)NECESITA CONTENIDO DE GEO.858

Robbie está construyendo una base para que un ventilador cilíndrico lo ponga en su habitación. El cono truncado tiene un radio mayor de 3 pies, un radio más pequeño de 2 pies y una altura inclinada de 3 pies. Él va a pintar el soporte y necesita encontrar la superficie de la base para averiguar cuánta pintura comprar. ¿Cómo puede Robbie averiguar el área de superficie?
En este concepto, aprenderás a encontrar los conos de superficie y los conos truncados.
Superficie
Los conos son figuras tridimensionales que tienen una base circular y un punto en la parte superior. Puede calcular el área de superficie de un cono usando una red o una fórmula. El área superficial es el total de las áreas de cada cara en una figura sólida.
Así es como se vería la red de un cono.

El círculo sombreado es la base. Recuerda, los conos siempre tienen bases circulares. La porción no sombreada del cono representa su lado. Técnicamente no se le llama cara a esto porque tiene un borde redondo.
Para encontrar el área de superficie de un cono, es necesario calcular el área de la base circular y el lateral y agregarlos juntos. La fórmula para encontrar el área de un círculo es\(A&=\pi r^{2}\), donde r es el radio del círculo. Utiliza esta fórmula para encontrar el área de la base circular.
Para encontrar el área del lado del cono, multiplicas el radio (\(r\)), la altura inclinada (\(s\)) y\(\pi\).
\(A=\pi rs\)
Veamos un ejemplo.
Encuentra el área de superficie del siguiente cono.
 Figura\(\PageIndex{4}\)
Figura\(\PageIndex{4}\)Primero, calcule el área de la base.
\(\begin{aligned}A&=\pi r^{2} \\ A&=\pi (5)^{2}\\ A&=78.5\end{aligned}\)
A continuación, calcular el área del sector, también conocida como área de superficie lateral.
\(\begin{aligned}A&=\pi (5)(11.7) \\ A&=183.8\end{aligned}\)
Después, agregue el área de la base a la superficie lateral.
\(\begin{aligned} A&=\text{base} +\text{lateral Surface} \\ A&=78.5+183.8 \\ A&=262.3\end{aligned}\)
La respuesta es 262.3.
El área de superficie del cono es\(262.3 \text{ in}^{2}\).
Un atajo sería simplemente usar la fórmula para encontrar el área de superficie de un cono. Aquí está la fórmula para encontrar el área superficial de un cono:\(SA&=\pi r^{2}+\pi rs\).
La primera parte de la fórmula,\(\pi r^{2}\), es simplemente la fórmula de área para círculos. Esto representa el área base. La segunda parte,\ pi rs, representa la superficie lateral del lado del cono. Simplemente puedes juntar las piezas y resolverlas para el área de ambas partes a la vez.
Un cono truncado es aquel en el que se corta la punta del cono dejando dos bases circulares y una cara lateral.
A continuación se muestra una imagen de cómo se ve un cono truncado.
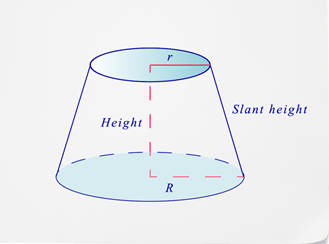
Observe que con un cono truncado tendrá dos bases circulares diferentes: un radio superior y una inferior. Tendrás que encontrar el área de ambas bases más el área del sector para encontrar la superficie.
La fórmula para encontrar el área de superficie de un cono truncado es:
\(SA=\pi [s(R+r)+r^{2}+r^{2}]\)
Observe que s significa altura inclinada, la R mayúscula representa el radio mayor y la r minúscula representa el radio más pequeño.
Veamos un ejemplo.
¿Cuál es la superficie de un cono truncado con una altura inclinada de 6 cm, un radio de 8 cm y un radio de 6 cm?
Primero, rellena todo lo que sabes en la fórmula del área de superficie.
\(\begin{aligned}SA&=\pi [s(R+r)+r^{2}+r^{2}] \\ SA&=\pi [6(8+6)+8^{2}+6^{2}]\end{aligned}\)
A continuación, use álgebra para resolver el área de superficie.
\(\begin{aligned}SA&=\pi [6(8+6)+8^{2}+6^{2}] \\ SA&=\pi [6(14)+64+36] \\ SA&=\pi [84+64+36] \\ SA&=\pi [184] \\ SA&=578.1\end{aligned}\)
La respuesta es 578.1.
El área de superficie del cono es\(578.1\text{ cm}^2\).
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre el stand de fans de Robbie.
Robbie está construyendo un soporte en forma de cono truncado. La base circular inferior tiene un radio de 3 pies. La parte superior circular tiene un radio de 2 pies. La altura inclinada para el soporte es de 3 pies. Robbie tiene que encontrar la superficie para que sepa cuánta pintura necesita.
Solución
Primero, sustituya lo que sabes en la fórmula de área de superficie.
\(\begin{aligned}SA&=\pi [s(R+r)+r^{2}+r^{2}] \\ SA&=\pi [3(3+2)+3^{2}+2^{2}]\end{aligned}\)
A continuación, use álgebra para resolver el área de superficie.
\(\begin{aligned}SA&=\pi [3(3+2)+3^{2}+2^{2}] \\ SA&=\pi [3(5)+9+4] \\ SA&=\pi [15+9+4] \\ SA&=\pi [28] \\ SA&=87.96\end{aligned}\)
La respuesta es 87.96.
Robbie necesita suficiente pintura para cubrir\(88\text{ ft}^2\).
Ejemplo\(\PageIndex{2}\)
Trey está decorando sombreros de fiesta cónicos para su fiesta envolviéndolos en papel de seda de colores. Cada sombrero tiene un radio de 4.2 centímetros y una altura inclinada de 8.6 centímetros. Si quiere envolver seis sombreros de fiesta, ¿cuánto papel necesitará?
Solución
Primero, sustituya lo que sabes en la fórmula de área de superficie.
\(\begin{aligned}SA&=\pi r^{2}+\pi rs \\ SA&=\pi (4.2)2+\pi (4.2)(8.6)\end{aligned}\)
A continuación, use álgebra para resolver el área de superficie.
\(\begin{aligned}SA&=\pi (4.2)^{2}+\pi (4.2)(8.6) \\ SA&=\pi (17.64)+\pi (36.12) \\ SA&=55.4+113.5 \\ SA&=168.9\end{aligned}\)
Después, encuentra el área total de los 6 sombreros.
\(SA_{total}&=6×SA^{one\: hat} 89 \\ SA_{total}&=6×168.9 \\SA_{total}&=1013.4\end{aligned}\)
La respuesta es 1013.4.
Trey necesitaría 1013.4 cm 2 de papel para hacer los seis sombreros.
Ejemplo\(\PageIndex{3}\)
Encuentra el área de superficie de un cono con un radio de 4 pulgadas y una altura inclinada de 6 pulgadas.
Solución
Primero, sustituya lo que sabes en la fórmula de área de superficie.
\(\begin{aligned}SA&=\pi r^{2}+\pi rs \\ SA&=\pi (4)2+\pi (4)(6)\end{aligned}\)
A continuación, use álgebra para resolver el área de superficie.
\(\begin{aligned}SA&=\pi (4)^{2}+\pi (4)(6) \\ SA&=\pi (16)+\pi (24) \\ SA&=50.3+75.4\\ SA&=125.7\end{aligned}\)
La respuesta es 125.7.
El área de superficie del cono es\(125.7 \text{ in}^{2}\).
Ejemplo\(\PageIndex{4}\)
Encuentra el área de superficie de un cono con un radio de 5 pies y una altura inclinada de 8 pies.
Solución
Primero, sustituya lo que sabes en la fórmula de área de superficie.
\(\begin{aligned}SA&=\pi r^{2}+\pi rs \\ SA&=\pi (5)2+\pi (5)(8)\end{aligned}\)
A continuación, use álgebra para resolver el área de superficie.
\(\begin{aligned}SA&=\pi (5)^{2}+\pi (5)(8) \\ SA&=\pi (25)+\pi (40) \\ SA&=78.5+125.7 \\ SA&=204.2\end{aligned}\)
La respuesta es 204.2.
El área de superficie del cono es\(204.2\text{ ft}^2\).
Ejemplo\(\PageIndex{5}\)
Encuentra el área de superficie de un cono con un radio de 3 pulgadas y una altura inclinada de 4.5 pulgadas.
Solución
Primero, sustituya lo que sabes en la fórmula de área de superficie.
\(\begin{aligned}SA&=\pi r^{2}+\pi rs \\ SA&=\pi (3)^{2}+\pi (3)(4.5)\end{aligned}\)
A continuación, use álgebra para resolver el área de superficie.
\(\begin{aligned} SA&=\pi (3)^{2}+\pi (3)(4.5) \\ SA&=\pi (9)+\pi (13.5) \\ SA&=28.3+42.4 \\ SA&=70.7\end{aligned}\)
La respuesta es 70.7.
El área de superficie del cono es\(70.7 \text{ in}^{2}\).
Revisar
Responde las preguntas a continuación de cada uno de los siguientes diagramas
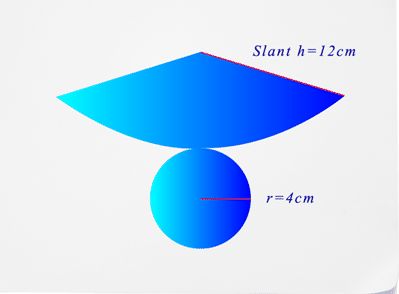
- ¿Cuál es el nombre de la figura representada en esta red?
- ¿Cuál es el diámetro de esta figura?
- ¿Cuál es la altura inclinada de la figura?
- ¿Cuál es la superficie de la figura?
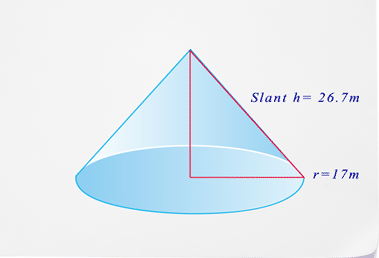
- ¿Cuál es el nombre de esta figura?
- ¿Cuál es la forma de la base?
- ¿Cuál es el diámetro de la base?
- ¿Cuál es la superficie de esta figura?

- ¿Cuál es el nombre de esta figura?
- ¿Cuál es la forma de la base?
- ¿Cuál es el diámetro de la base?
- ¿Cuál es la superficie de esta figura?
Encuentra el área de superficie de cada cono.
- \(r=4\text{ in}\),\(sh=5\text{ in}\)
- \(r=5 \text{ m}\),\(sh=7 \text{ m}\)
- \(r=3 \text{ cm}\),\(sh=6\text{ cm}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.9.
Recursos
vocabulario
| Término | Definición |
|---|---|
| Cono | Un cono es una figura tridimensional sólida con una base circular y un vértice. |
| Net | Una red es un diagrama que muestra una vista “aplanada” de un sólido. En una red, cada cara y base se muestra con todas sus dimensiones. Una red también puede servir como patrón para construir un sólido tridimensional. |
| Sector | Un sector de un círculo es una porción de un círculo contenida entre dos radios del círculo. Los sectores se pueden medir en grados. |
| Superficie | El área superficial es el área total de todas las superficies de un objeto tridimensional. |
| Altura Inclinada | La altura inclinada es la altura de una cara lateral de una pirámide. |
Recursos adicionales
Video: Área de superficie del cono - Descripción general
Práctica: Superficie de Conos

