9.24: Volumen de Conos
- Page ID
- 107240
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El volumen es igual al área de los tiempos base\(\dfrac{1}{3}\) de la altura.

Encontrar el volumen de un cono
Para averiguar el volumen de un cono, primero veamos cómo puedes compararlo con otra figura sólida. La figura sólida más cercana a un cono es un cilindro. Tanto los conos como los cilindros tienen bases circulares. La diferencia entre los dos es mientras que un cilindro tiene dos bases circulares, un cono solo tiene una.
Aquí hay un cilindro y la fórmula para encontrar el volumen de un cilindro.
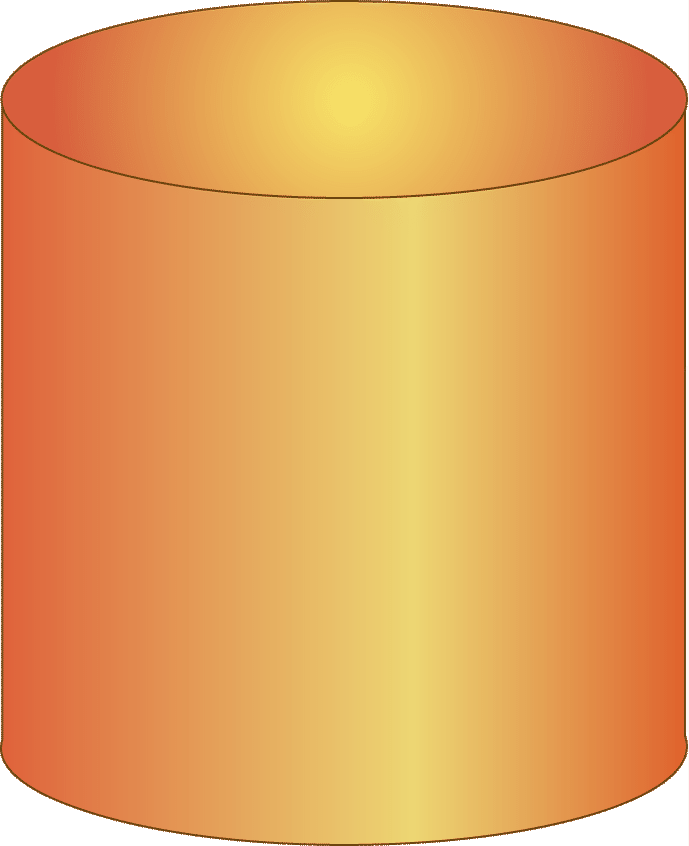
\(V&=\pi r^{2} h\)
En la imagen de abajo, puedes ver cómo se relacionan un cilindro y un cono:
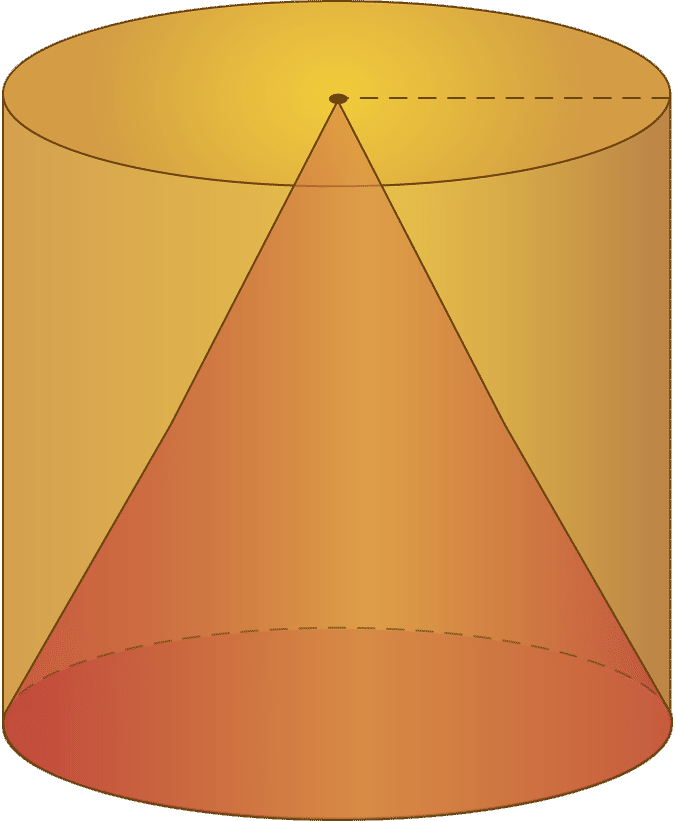
Para encontrar el volumen del cono, usas una fórmula similar a la de una pirámide, excepto que vas a tomar en consideración que la base de un cono es un círculo. Por lo tanto, necesitarás encontrar el área del círculo para encontrar el volumen del cono. La fórmula para el área de un círculo es\(\pi r^{2}\). Toma esa medida y multiplícalo por la altura del cono. A continuación, debido a que el cono llena una porción del cilindro, multiplique el producto por un tercio.
\(V&=\dfrac{1}{3} \pi r^{2} h\)
Veamos un ejemplo. ¿Cuál es el volumen del cono abajo?
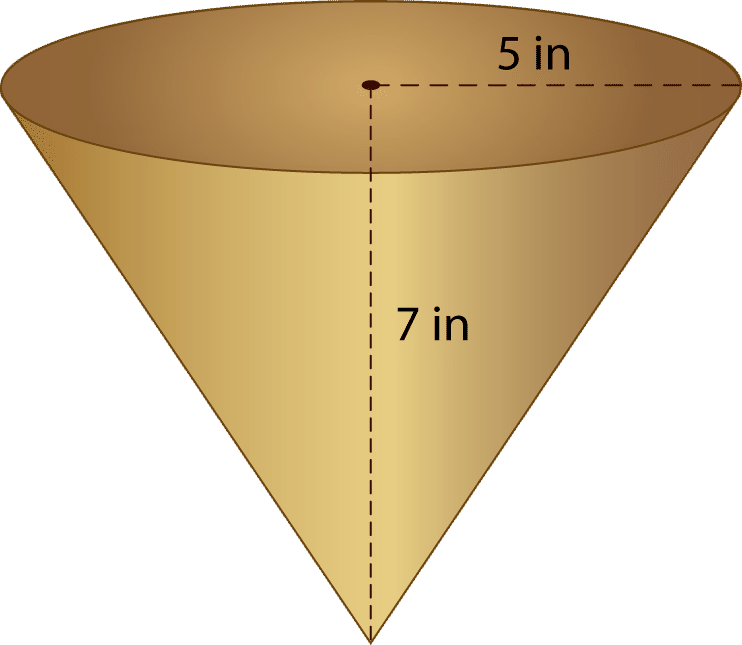
Primero, sustituya los valores dados en la fórmula.
\(\begin{aligned}V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(52)(7) \\ V&=\dfrac{1}{3} (3.14)(25)(7) \\ V&=\dfrac{1}{3} (3.14)(175)\\ V&=\dfrac{549.5}{3} \\ V&=183.16 \text{ in}^{3}\end{aligned}\)
La respuesta es que el volumen del cono es de 183.16 pulgadas cúbicas.
Veamos otro ejemplo. Encuentra el volumen del siguiente cono.
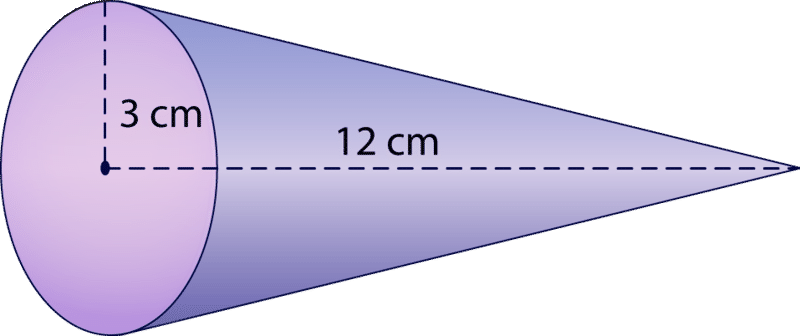
Primero, sustituya los valores dados en la fórmula.
\(\begin{aligned}V&=\dfrac{1}{3} (3.14)(3^{2})(12) \\ V&=\dfrac{1}{3} (3.14)(9)(12) \\ V&=\dfrac{1}{3} (3.14)(108) \\ V&=\dfrac{339.12}{3} \\ V&=113.04 cm^{3}\end{aligned}\)
El volumen del cono es\(113.04\text{ cm}^3\).
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre las nuevas tazas de postre de Francine.
Necesita averiguar el volumen de helado que cabrá en una taza de postre. El diámetro de la copa es de 3 pulgadas y la altura es de 6 pulgadas.
Solución
Primero, busque el valor del radio dividiendo el diámetro por 2, y sustituya los valores por pi, el radio y la altura del cono en la fórmula para el volumen de un cono.
\(\begin{aligned}r&=1.5 \\ r&=3\divide 2 \\ V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(1.52)(6)\end{aligned}\)
A continuación, cuadrar el radio y multiplicar los valores juntos.
\(\begin{aligned}V&=\dfrac{1}{3} (3.14)(1.52)(6) \\ V&=\dfrac{1}{3} (3.14)(2.25)(6) \\ V&=\dfrac{1}{3} (3.14)(13.5) \\ V&=42.393\end{aligned}\)
Después, divida por 3 y registre la respuesta, recordando incluir la unidad de medida apropiada.
\(\begin{aligned}V&=42.393 \\ V&=14.13 \text{ in}^{3}\end{aligned}\)
La respuesta es que el volumen de helado que llenará la copa del desierto en forma de cono de Francine es de 16.75 pulgadas cúbicas.
Ejemplo\(\PageIndex{2}\)
Encuentra el volumen de un cono con un radio de 2 pulgadas y una altura de 4 pulgadas.
Solución
Primero, sustituya los valores por pi, el radio y la altura del cono en la fórmula para el volumen de un cono.
\(\begin{aligned}V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(2^{2})(4)\end{aligned}\)
A continuación, cuadrar el radio y multiplicar los valores juntos.
\(\begin{aligned}V&=\dfrac{1}{3} (3.14)(2^{2})(4) \\ V&=\dfrac{1}{3} (3.14)(4)(4) \\ V&=\dfrac{1}{3} (3.14)(16) \\ V&=50.243\end{aligned}\)
Después, divida por 3 y registre la respuesta, recordando incluir la unidad de medida apropiada.
\(\begin{aligned}V&=\dfrac{50.24}{3} \\ V&=16.75 \text{ in}^{3}\end{aligned}\)
La respuesta es que el volumen del cono es de 16.75 pulgadas cúbicas.
Ejemplo\(\PageIndex{3}\)
Encuentra el volumen de un cono con un radio de 5 pies y una altura de 8 pies.
Solución
Primero, sustituya los valores por pi, el radio y la altura del cono en la fórmula para el volumen de un cono.
\(\begin{aligned}V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(52)(8)\end{aligned}\)
A continuación, cuadrar el radio y multiplicar los valores juntos.
\(\begin{aligned}V&=\dfrac{1}{3} (3.14)(52)(8) \\ V&=\dfrac{1}{3} (3.14)(25)(8) \\ V&=\dfrac{1}{3} (3.14)(200) \\ V&=\dfrac{628}{3}\end{aligned}\)
Después, divida por 3 y registre la respuesta, recordando incluir la unidad de medida apropiada.
\(\begin{aligned}V&=\dfrac{628}{3} \\ V&=209.33 \text{ in}^{3}\end{aligned}\)
La respuesta es que el volumen del cono es de 209.33 pulgadas cúbicas.
Ejemplo\(\PageIndex{4}\)
Un cono con un radio de 4 m y una altura de 9 m.
Solución
Primero, sustituya los valores por pi, el radio y la altura del cono en la fórmula para el volumen de un cono.
\(\begin{aligned}V&=\dfrac{1}{3} \pi r^{2} h \\ V&=\dfrac{1}{3} (3.14)(4^{2})(9)\end{aligned}\)
A continuación, cuadrar el radio y multiplicar los valores juntos.
\(\begin{aligned}V&=\dfrac{1}{3} (3.14)(4^{2})(9) \\ V&=\dfrac{1}{3} (3.14)(16)(9) \\ V&=\dfrac{1}{3} (3.14)(144) \\ V&=\dfrac{452.16}{3}\end{aligned}\)
Después, divida por 3 y registre la respuesta, recordando incluir la unidad de medida apropiada.
\(\begin{aligned} V&=\dfrac{452.16}{3} \\ V&=150.72 \text{ m}^{3}\end{aligned}\)
La respuesta es que el volumen del cono es de 150.72 metros cúbicos.
Revisar
Encuentra el volumen de cada cono.
- Un cono con un radio de 3 pulgadas y una altura de 7 pulgadas.
- Un cono con un radio de 5 pies y una altura de 9 pies.
- Un cono con un radio de 6 metros y una altura de 10 metros.
- Un cono con un radio de 10 pulgadas y una altura de 12 pulgadas.
- Un cono con un radio de 12 mm y una altura de 14 mm.
- Un cono con un radio de 5 pies y una altura de 12 pies.
- Un cono con un radio de 4.5 pulgadas y una altura de 7 pulgadas.
- Un cono con un radio de 3.5 pulgadas y una altura de 5.5 pulgadas.
- Un cono con un radio de 7 cm y una altura de 13 cm.
- Un cono con un radio de 8 cm y una altura de 11 cm.
- Un cono con un radio de 7.5 pulgadas y una altura de 11 pulgadas.
- Un cono con un radio de 11.5 pulgadas y una altura de 15 pulgadas.
- Un cono con un radio de 12.5 pies y una altura de 15 pies.
Resuelve cada problema de palabras.
- Un cono tiene un radio de 6 metros y una altura de 14 metros. ¿Cuál es su volumen?
- Los recipientes de glaseado para el decorador de tartas de Tina son conos. Cada contenedor tiene un radio de 2.4 pulgadas y una altura de 7 pulgadas. Si Tina compra contenedores de glaseado rojo, amarillo y azul, ¿cuánto glaseado comprará?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.15.
El vocabulario
| Término | Definición |
|---|---|
| Cono | Un cono es una figura tridimensional sólida con una base circular y un vértice. |
| Pyramid | Una pirámide es un objeto tridimensional con una base que es un polígono y caras triangulares que se encuentran en un vértice. |
| Volumen | Volumen es la cantidad de espacio dentro de los límites de un objeto tridimensional. |
Recursos adicionales
Elemento interactivo
Video: Determinar el volumen de un cono
Práctica: Volumen de Conos

