4.3: Triángulos Rectos Especiales
- Page ID
- 107274
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El Teorema de Pitágoras es genial para encontrar el tercer lado de un triángulo rectángulo cuando ya conoces otros dos lados. Hay algunos triángulos como los triángulos 30-60-90 y 45-45-90 que son tan comunes que es útil conocer las proporciones laterales sin hacer cada vez el Teorema de Pitágoras. El uso de estos patrones también te permite resolver totalmente los lados faltantes de estos triángulos especiales cuando solo conoces la longitud de un lado.
Dado un triángulo rectángulo 45-45-90 con lados de 6 pulgadas, 6 pulgadas y\(x\) pulgadas, ¿cuál es el valor de\(x\)?
Triángulos Rectos Especiales
Hay tres tipos de triángulos rectos especiales, triángulos 30-60-90, triángulos 45-45-90 y triángulos triangulares pitagóricos.
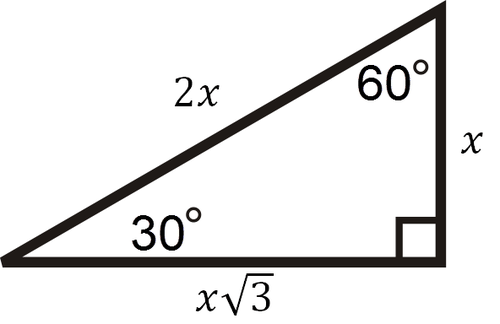
Triángulos 30-60-90
Un triángulo rectángulo 30-60-90 tiene relaciones laterales\(x, x \sqrt{3}, 2 x\).
Confirmar con el Teorema de Pitágoras:
\(\begin{aligned} x^{2}+(x \sqrt{3})^{2} &=(2 x)^{2} \\ x^{2}+3 x^{2} &=4 x^{2} \\ 4 x^{2} &=4 x^{2} \end{aligned}\)
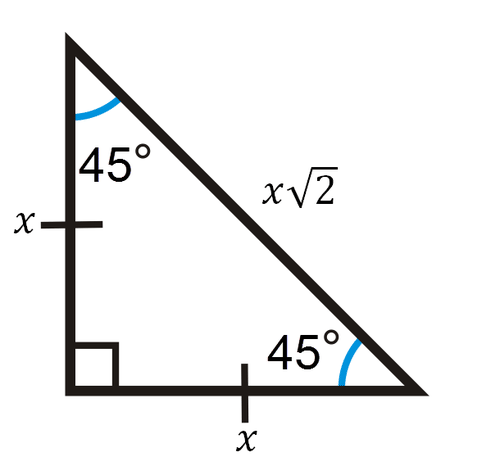
45-45-90 Triángulos
Un triángulo rectángulo de 45 - 45 -90 tiene relaciones laterales\(x, x, x \sqrt{2}\).
Confirmar con el Teorema de Pitágoras:
\(\begin{aligned} x^{2}+x^{2} &=(x \sqrt{2})^{2} \\ 2 x^{2} &=2 x^{2} \end{aligned}\)
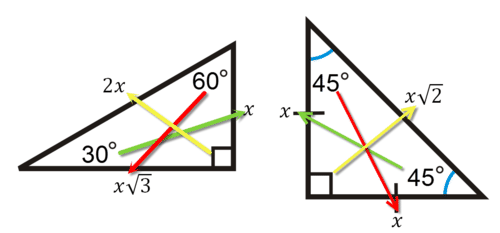
Tenga en cuenta que el orden de las relaciones laterales\(x, x \sqrt{3}, 2 x\) y\(x, x, x \sqrt{2}\) es importante porque cada relación lateral tiene un ángulo correspondiente. En todos los triángulos, los lados más pequeños corresponden a los ángulos más pequeños y los lados más grandes siempre corresponden a los ángulos más grandes.
Triángulos triples pitagóricos
Los triples numéricos pitagóricos son triángulos rectos especiales con lados enteros. Si bien los ángulos no son enteros, las relaciones laterales son muy útiles de conocer porque aparecen en todas partes. Conocer estos triples numéricos también ahorra mucho tiempo de hacer repetidamente el Teorema de Pitágoras. Aquí hay algunos ejemplos de triples numéricos pitagóricos:
- 3, 4, 5
- 5, 12, 13
- 7, 24, 25
- 8, 15, 17
- 9, 40, 41
Se pueden encontrar más triples de números pitagóricos escalando cualquier otro triple de número pitagórico. Por ejemplo:
\(3,4,5 \rightarrow 6,8,10\)(escalado por un factor de 2)
Incluso se pueden encontrar más triples de números pitagóricos tomando cualquier entero impar como 11, al cuadrarlo para obtener 121, reducir a la mitad el resultado para obtener 60.5. El número original 11 y los dos números que están 0.5 arriba y abajo (60 y 61) siempre serán un número pitagórico triple.
\(11^{2}+60^{2}=61^{2}\)
Ejemplos
Anteriormente te preguntaron sobre un triángulo rectángulo 45-45-90 con lados de 6 pulgadas, 6 pulgadas y\(x\) pulgadas. Si puedes reconocer el patrón para triángulos rectos 45-45-90, un triángulo rectángulo con patas de 6 pulgadas y 6 pulgadas tiene una hipotenusa que es\(6 \sqrt{2}\) pulgadas\(x=6 \sqrt{2}\).
Un triángulo rectángulo 30-60-90 tiene hipotenusa de longitud 10. ¿Cuáles son las longitudes de los otros dos lados?
La hipotenusa es el lado opuesto al 90. A veces es útil dibujar un cuadro o hacer una mesa.
| 30 | 60 | 90 |
| \(x\) | \(x \sqrt{3}\) | \(2 x\) |
| 10 |
De la tabla se pueden escribir ecuaciones posteriores muy pequeñas para resolver por los lados faltantes.
\(\begin{aligned} 10 &=2 x \\ x &=5 \\ x \sqrt{3} &=5 \sqrt{3} \end{aligned}\)
Los otros lados son 5 y\(5 \sqrt{3}\).
Un triángulo rectángulo 30-60-90 tiene una longitud lateral de 18 pulgadas correspondiente a 60 grados. ¿Cuáles son las longitudes de los otros dos lados?
Haz una tabla con las proporciones laterales y la información dada, luego escribe ecuaciones y resuelve las longitudes laterales faltantes.
| 30 | 60 | 90 |
| \(x\) | \(x \sqrt{3}\) | \(2 x\) |
| 18 |
\(\begin{aligned} 18 &=x \sqrt{3} \\ \frac{18}{\sqrt{3}} &=x \\ x &=\frac{18}{\sqrt{3}}=\frac{18}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}}=\frac{18 \sqrt{3}}{3}=6 \sqrt{3} \\ x &=6 \sqrt{3} \end{aligned}\)
Tenga en cuenta que es necesario racionalizar los denominadores.
Ahora usa el\(x\) valor calculado para resolver\(2 x\).
\(2 x=2(6 \sqrt{3})\)
\(2 x=12 \sqrt{3}\)
Los otros lados son\(6 \sqrt{3}\) y\(12 \sqrt{3}\).
Usando tu conocimiento de las proporciones especiales del triángulo rectángulo, resuelve los lados faltantes del triángulo rectángulo.
Los otros lados son cada uno\(\frac{5 \sqrt{2}}{2}\).
| 45 | 45 | 90 |
| \(x\) | \(x\) | \(x \sqrt{2}\) |
| 5 |
\(\begin{aligned} x \sqrt{2} &=5 \\ x &=\frac{5}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}}=\frac{5 \sqrt{2}}{2} \end{aligned}\)
Los otros lados son cada uno\(\frac{5 \sqrt{2}}{2}\)
Usando tu conocimiento de las proporciones especiales del triángulo rectángulo, resuelve los lados faltantes del triángulo rectángulo.
Los otros lados son 9 y\(6 \sqrt{3}\).
| 30 | 60 | 90 |
| \(x\) | \(x \sqrt{3}\) | \(2 x\) |
| \(3 \sqrt{3}\) |
\(\begin{aligned} x &=3 \sqrt{3} \\ 2 x &=6 \sqrt{3} \\ x \sqrt{3} &=3 \sqrt{3} \cdot \sqrt{3}=9 \end{aligned}\)
Los otros lados son 9 y\(6 \sqrt{3}\).
Revisar
Para 1-4, encuentra los lados faltantes del triángulo 45-45-90 con base en la información dada en cada fila.
| Número de problema | Lado opuesto\(45^{\circ}\) | Lado opuesto\(45^{\circ}\) | Lado opuesto\(90^{\circ}\) |
| 1. | 3 | ||
| 2. | 7.2 | ||
| 3. | 16 | ||
| 4. | \(5 \sqrt{2}\) |
Para 5-8, encuentra los lados faltantes del triángulo 30-60-90 con base en la información dada en cada fila.
| Número de problema | Lado opuesto\(30^{\circ}\) | Lado opuesto\(60^{\circ}\) | Lado opuesto\(90^{\circ}\) |
| 1. | \(3 \sqrt{2}\) | ||
| 2. | 4 | ||
| 3. | 15 | ||
| 4. | \(12 \sqrt{3}\) |
Usa la imagen de abajo para el 9-11.
9. ¿Qué ángulo corresponde al lado que es 12 unidades?
10. ¿Qué lado corresponde al ángulo recto?
11. ¿Qué ángulo corresponde al lado que es 5 unidades?
12. Un triángulo rectángulo tiene un ángulo de\(\frac{\pi}{6}\) radianes y una hipotenusa de 20 pulgadas. ¿Cuáles son las longitudes de los otros dos lados del triángulo?
13. Un triángulo tiene dos ángulos que miden\(\frac{\pi}{4}\) radianes. El lado más largo es de 3 pulgadas de largo. ¿Cuáles son las longitudes de los otros dos lados?
Para 14-19, verificar el número de Pitágoras Triple usando el Teorema de Pitágoras.
14. 3, 4, 5
15. 5, 12, 13
16. 7, 24, 25
17. 8, 15, 17
18. 9, 40, 41
19. 6, 8, 10
20. Encuentra otro Número Pitagórico Triple usando el método explicado para encontrar “11, 60, 61”.
...