6: Intervalos de confianza y tamaño de muestra
( \newcommand{\kernel}{\mathrm{null}\,}\)
Las inferencias que se discutieron en los capítulos 5 y 6 se basaron en el supuesto de una hipótesis a priori que el investigador tenía sobre una población. Sin embargo, hay momentos en los que los investigadores no tienen hipótesis. En tales casos simplemente les gustaría una buena estimación del parámetro.
A estas alturas ya deberías darte cuenta de que la estadística (que proviene de la muestra) probablemente no será igual al parámetro de la población, pero estará relativamente cerca ya que forma parte de la colección normalmente distribuida de posibles estadísticas. En consecuencia, lo mejor que se puede afirmar es que la estadística es una estimación puntual del parámetro. Debido a que la mitad de las estadísticas que podrían seleccionarse son superiores al parámetro y la mitad son menores, y debido a que la variación que se puede esperar para las estadísticas depende, en parte, del tamaño de la muestra, entonces el conocimiento de la estadística es insuficiente para determinar el grado en que es una buena estimación para el parámetro. Por esta razón, las estimaciones se proporcionan con intervalos de confianza en lugar de estimaciones puntuales.
Probablemente esté más familiarizado con el concepto de intervalos de confianza de los resultados de las encuestas anteriores a las elecciones. Un reportero podría decir que 48% de las personas en una encuesta planean votar por el candidato A, con un margen de error de más o menos 3%. La interpretación es que entre 45% y 51% de la población de votantes votará por el candidato A. El tamaño del margen de error proporciona información sobre la brecha potencial entre la estimación puntual (estadística) y el parámetro. El intervalo da el rango de valores que es más probable que contengan el parámetro true. Para un intervalo de confianza de (0.45,0.51) existe la posibilidad de que el candidato pueda tener la mayoría del apoyo. El margen de error, y consecuentemente el intervalo, depende del grado de confianza que se desee, del tamaño de la muestra y del error estándar de la distribución muestral.
La lógica detrás de la creación de intervalos de confianza se puede demostrar usando la regla empírica, también conocida como la regla 68-95-99.7 que aprendió en el Capítulo 5. Sabemos que de todas las estadísticas posibles que comprenden una distribución de muestreo, 95% de ellas se encuentran dentro de aproximadamente 2 errores estándar de la media de la distribución. De esto podemos deducir que la media de la distribución está dentro de 2 errores estándar del 95% de las estadísticas posibles. Por analogía, esto equivale a decir que si estás a menos de dos metros del alumno que está sentado a tu lado, entonces ese alumno está a menos de dos metros de ti. En consecuencia, al tomar la estadística y sumar y restar dos errores estándar, se crea un intervalo que debe contener el parámetro para el 95% de las estadísticas que podríamos obtener utilizando un buen proceso de muestreo aleatorio.
Al utilizar la regla empírica, el número 2, en la frase “2 errores estándar”, se denomina valor crítico. Sin embargo, un buen intervalo de confianza requiere un valor crítico con mayor precisión que la que proporciona la regla empírica. Además, puede haber un deseo de que el grado de confianza sea algo además del 95%. Las alternativas comunes incluyen intervalos de confianza de 90% y 99%. Si el grado de confianza es del 95%, entonces los valores críticos separan el 95% medio de las estadísticas posibles del resto de la distribución. Si el grado de confianza es del 99%, entonces los valores críticos separan el 99% medio de las estadísticas posibles del resto de la distribución. Si el valor crítico se encuentra en la distribución normal estándar (unz valor) o en las distribuciones t (un valor t) se basa en si el intervalo de confianza es para una proporción o una media.
Se debe determinar el valor crítico y el error estándar de la distribución muestral para poder calcular el margen de error.
El valor crítico se encuentra determinando primero el área en una cola. El área en la cola izquierda (AL) se encuentra restando el grado de confianza de 1 y luego dividiendo éste por 2.
AL=1−degree of confidence2.
Por ejemplo, sustituir en la fórmula un intervalo de confianza del 95% produce
AL=1−0.952=0.025
El valor Z crítico para un área a la izquierda de 0.025 es -1.96. Debido a la simetría, el valor crítico de un área a la derecha de 0.025 es +1.96. Esto quiere decir que si encontramos los valores críticos correspondientes a un área en la cola izquierda de 0.025, encontraremos las líneas que separan al grupo de estadísticas con un 95% de probabilidad de ser seleccionado del grupo que tiene un 5% de probabilidad de ser seleccionado.
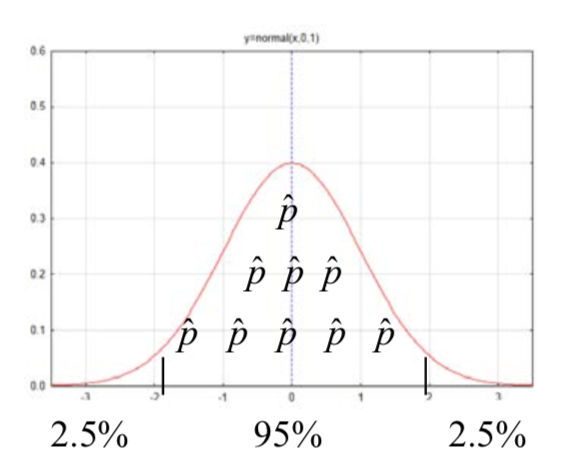
Un área en la cola izquierda de 0.025, que se encuentra en el cuerpo de la tabla de distribución z, corresponde con unz∗ valor de -1.96. Esto se muestra en la sección de la tabla Z que se muestra a continuación.
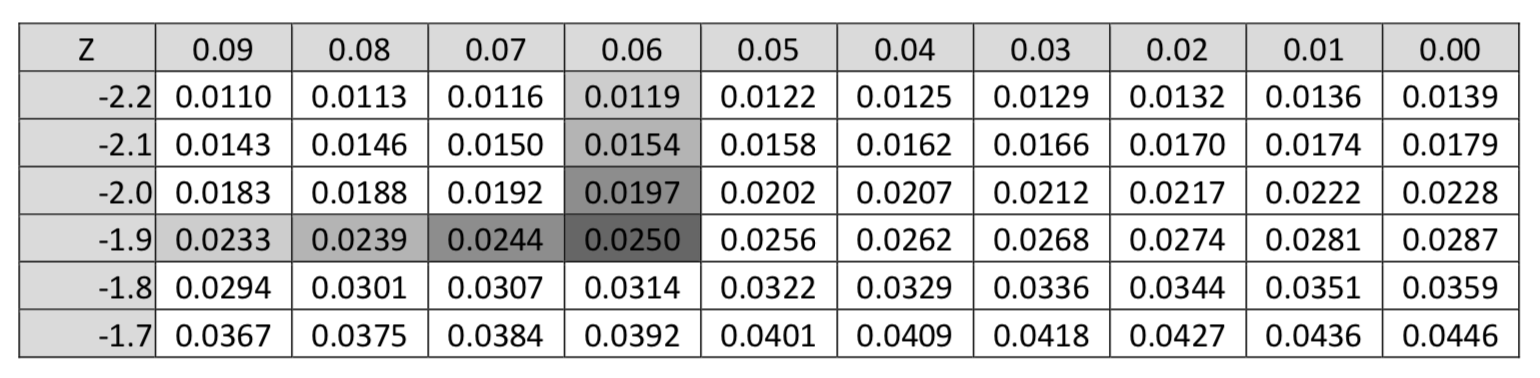
Elz valor crítico de -1.96 también se llama percentil 2.5. Eso significa que 2.5% de todas las estadísticas posibles están por debajo de ese valor.
Los valores críticos también se pueden encontrar usando una calculadora TI 84. Utilice2nd Distr, #3 invnorm (percentil,μ,σ). Por ejemplo invnorm (0.025,0,1) da -1.95996 que redondea a -1.96.
Los intervalos de confianza para las proporciones siempre tienen un valor crítico encontrado en la distribución normal estándar. Elz valor que se encuentra se le da la notaciónz∗. Estos valores críticos varían en función del grado de confianza. Los otros intervalos de confianza más comunes son 90% y 99%. Complete la siguiente tabla para encontrar estos valores críticos de uso común.
| Grado de Confianza | Área en la cola izquierda | z∗ |
|---|---|---|
| 0.90 | \ (z^ {\ ast}\)” style="vertical-align: middle; "> | |
| 0.95 | 0.025 | \ (z^ {\ ast}\)” style="vertical-align: middle; ">1.96 |
| 0.99 | \ (z^ {\ ast}\)” style="vertical-align: middle; "> |
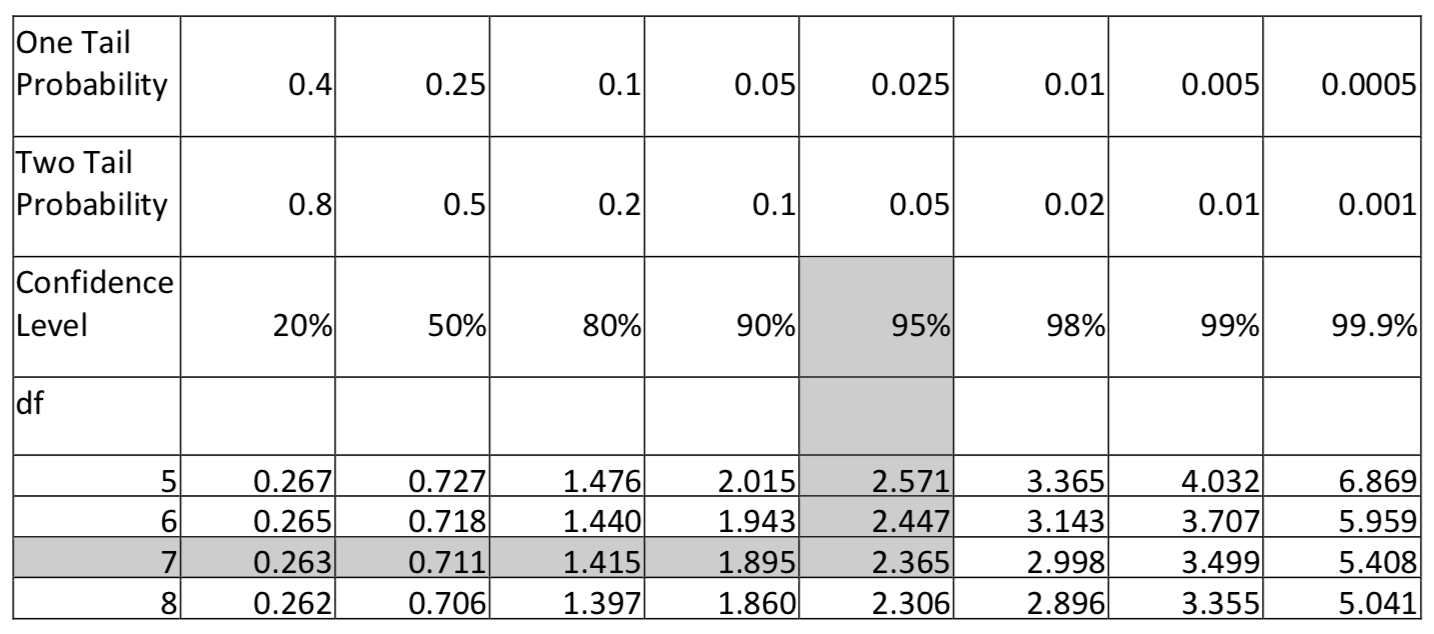
Los intervalos de confianza para las medias requieren un valor críticot∗, que se encuentra en las tablas t. Estos valores críticos dependen tanto del grado de confianza como del tamaño de la muestra, o más precisamente, de los grados de libertad. La parte superior de la tabla t proporciona una variedad de niveles de confianza junto con el área en una o ambas colas. El enfoque más fácil para encontrar elt∗ valor crítico es encontrar la columna con el nivel de confianza apropiado y luego encontrar dónde esa columna se cruza con la fila que contiene los grados de libertad apropiados. Por ejemplo, elt∗ valor para un intervalo de confianza del 95% con 7 grados de libertad es de 2.365.
El segundo componente del margen de error, que es el error estándar para la distribución de muestreo, asume el conocimiento de la media de la distribución (e.g.μˆp=p yμˉx=μ). Al probar hipótesis sobre la media de la distribución, asumimos estos valores porque asumimos que la hipótesis nula es verdadera. Sin embargo, al crear intervalos de confianza, admitimos no conocer estos valores y por lo tanto, en consecuencia no podemos usar el error estándar. Por ejemplo, el error estándar para elσˆp=√p(1−p)n. Como no sabemosp, no podemos usar esta fórmula. Asimismo, el error estándar para la distribución de medias muestrales esσˉx=σ√n. Para encontrarσ necesitamos saber la media poblacionalμ, pero una vez más no la conocemos, y ni siquiera tenemos una hipótesis al respecto, así que consecuentemente no podemos encontrarσ. La estrategia en ambos casos es encontrar una estimación del error estándar utilizando una estadística para estimar el parámetro faltante. Así,ˆp se utiliza para estimarp ys se utiliza para estimarσ. Los errores estándar estimados luego se convierten en:sˆp=√ˆp(1−ˆp)n ysˉx=s√n.
Ahora se han sentado las bases para desarrollar las fórmulas de intervalo de confianza para las situaciones para las que probamos hipótesis en el capítulo anterior, a saberp,pA−pB,μ, yμA−μB. La siguiente tabla resume estos cuatro parámetros, sus distribuciones y los errores estándar estimados.
| Parámetro | Distribución | Error estándar estimado |
|---|---|---|
| Proporción para una población,p | 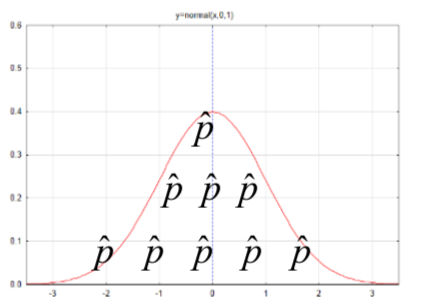 |
sˆp=√ˆp(1−ˆp)n |
| Diferencia entre proporciones para dos poblaciones,pA−pB | 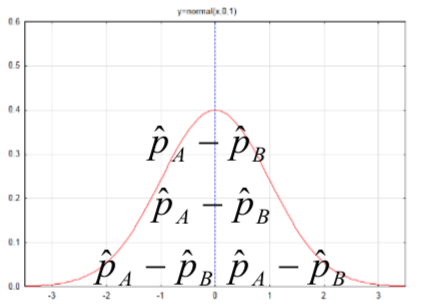 |
sˉpA−ˉpB=√ˆpA(1−ˆpA)nA+ˆpB(1−ˆpB)nB |
| M ean para una población o diferencia de medias para datos dependientes,μ | 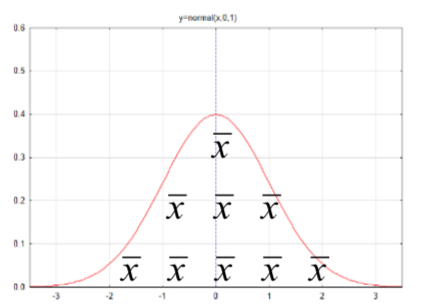 |
sˉx=s√n |
| D diferencia entre medias de dos poblaciones independientes,μA−μB | 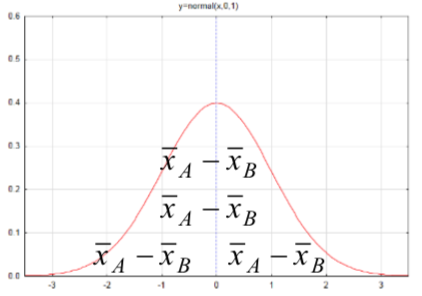 |
sˉxA−ˉxB=√[(nA−1)s2A+(nB−1)s2BnA+nB−2][1nA+1nB] |
El proceso de razonamiento para determinar las fórmulas para los intervalos de confianza es el mismo en todos los casos.
- Determinar el grado de confianza. Los más comunes son 95%, 99% y 90%.
- Utilice el grado de confianza junto con la tabla apropiada (z* o t*) para encontrar el valor crítico.
- Multiplique el valor crítico por el error estándar para encontrar el margen de error.
- El intervalo de confianza es el estadístico más o menos el margen de error.
Observe que todos los intervalos de confianza tienen el mismo formato, aunque algunos parezcan más difíciles que otros.
±margen estadístico de error
estadístico valor± crítico× estimado error estándar
Intervalos de confianza sobre la proporción para una población:
ˆp±z∗√ˆp(1−ˆp)n
Intervalos de confianza para la diferencia de proporciones entre dos poblaciones:
(ˆpA−ˆpB±z∗√ˆpAˆqAnA+ˆpBˆqBnB
Recuerden esoq=1–p.
Intervalos de confianza para la media de una población:
ˉx±t∗s√n
Intervalo de confianza para la diferencia entre dos medias independientes:
(ˉxA+ˉxB±t∗(√[(nA−1)s2A+(nB−1)s2BnA+nB−2][1nA+1nB])
dondet∗ es el percentil apropiado de la distribución t (nA+nB - 2).
Las fórmulas de intervalo de confianza se organizan a continuación de la misma manera que las fórmulas de prueba de hipótesis se organizaron en el Capítulo 6. Deberías ver una similitud entre las fórmulas correspondientes.
| Proporciones (para datos categóricos) | Medios (para datos cuantitativos) | |
|---|---|---|
| 1 - muestra |
ˆp±z∗√ˆp(1−ˆp)n Supuestos: np≥5,n(1−p)≥5 |
ˉx±t∗s√n df = n - 1 Supuestos: Sin<30, la población está aproximadamente distribuida normalmente. |
| 2 - muestras |
(ˆpA−ˆpB±z∗√ˆpAˆqAnA+ˆpBˆqBnB Asunción: np≥5, tanton(1−p)≥5 para la población |
(ˉxA+ˉxB±t∗(√[(nA−1)s2A+(nB−1)s2BnA+nB−2][1nA+1nB]) df =nA +nB - 2 Supuestos: Sin<30, la población está aproximadamente distribuida normalmente. |
¿Qué significa un intervalo de confianza? Para un intervalo de confianza del 95%, 95% de todas las estadísticas posibles están dentro de z* (o t*) errores estándar de la media de la distribución. Por lo tanto, existe una probabilidad del 95% de que los datos que se seleccionan aleatoriamente produzcan una de esas estadísticas y el intervalo de confianza que se crea contendrá el parámetro. Se desconoce si el intervalo en última instancia incluye el parámetro o no. Solo sabemos que si los procesos de muestreo se repitieran una gran cantidad de veces produciendo muchos intervalos de confianza, alrededor del 95% de ellos contendrían el parámetro.
Ejemplo 1
En un experimento de automaticidad, los estudiantes de colegios comunitarios tuvieron dos oportunidades para ir al laboratorio de computación para probar sus habilidades de automaticidad (fluidez matemática). Los estudiantes fueron asignados aleatoriamente para usar uno de los dos programas de práctica para determinar si un programa conduce a una mejora mayor que el otro. Estos programas se denominarán programa A y programa B.
a. ¿Cuál es el intervalo de confianza del 95% para la proporción de estudiantes que mejoran desde su primer intento hasta su segundo intento si 99 de 113 estudiantes mejoraron?
Para ayudar a elegir la fórmula correcta del intervalo de confianza, observe que este problema se trata de proporciones y solo hay un grupo de estudiantes.
La fórmula que cumple con estos criterios es:ˆp±z∗√ˆp(1−ˆp)n. Antes de sustituir, es necesario calcularˆp. Desdeˆp=xn=99113=0.876 (redondear a 3 decimales), entonces la fórmula del intervalo de confianza se convierte en0.876±1.96√0.876(1−0.876113. Esto simplifica a 0.876± 0.061. El margen de error es de 6.1%. El intervalo de confianza es (0.815,0.937). La conclusión es que estamos 95% seguros de que la verdadera proporción de estudiantes que mejorarían de una prueba a la siguiente está entre 0.815 (81.5%) y 0.937 (93.7%).
Para encontrar este intervalo en la calculadora TI 84, seleccione Stat, Tests, A 1-PropZint.
b. ¿Cuál es el intervalo de confianza del 90% para la diferencia en la proporción de alumnos que mejoraron desde su primer intento hasta su segundo intento utilizando el Programa A (37/45) y el Programa B (61/67)?
Para ayudar a elegir la fórmula correcta del intervalo de confianza, observe que este problema se trata de proporciones y hay dos poblaciones diferentes: una usando el Programa A y la otra usando el Programa B.
La fórmula que cumple con estos criterios es:(ˆpA−ˆpB±z∗√ˆpAˆqAnA+ˆpBˆqBnB. DesdeˆpA=xn=3745=0.822 yˆpB=xn=6167=0.919, entonces la fórmula del intervalo de confianza se convierte en
0.822−0.910)±1.645√0.822(1−0.822)45+0.910(1−0.910)67
Después de la simplificación el intervalo de confianza puede escribirse como un estadístico ± margen de error: -0.088± 0.110. El margen de error es del 11.0%. El intervalo de confianza es (-0.198,0.022). La conclusión es que estamos 90% seguros de que la verdadera diferencia de proporciones entre los que utilizan el Programa A y los que utilizan el Programa B está entre -0.198 y 0.022. Observe que 0 cae dentro de ese rango, lo que indica que potencialmente no hay diferencia entre estas dos proporciones.
Para encontrar este intervalo en la calculadora TI 84, seleccione Stat, Tests, B 2-PROPzint.
c. Cuál es el intervalo de confianza del 99% para la mejora promedio de los estudiantes de Álgebra Introductoria que utilizan el programa B (media = 5.0, DE = 3.18, n = 19).
Para ayudar a elegir la fórmula correcta del intervalo de confianza, observe que este problema se trata de medios y solo hay una población (estudiantes de Álgebra Introductoria que utilizan el programa B).
La fórmula que cumple con estos criterios es:ˉx±t∗s√n. Hay 18 grados de libertad (df = n-1) por lo que elt∗ valor es 2.878. Después de sustituir por todas las variables se convierte la fórmula5.0±2.8783.18√19. Esto simplifica a 5.0± 2.1. El intervalo de confianza es (2.9, 7.1).
Para encontrar este intervalo en la calculadora TI 84, seleccione Estadísticas, Pruebas, #8 Tintervalo.
d. ¿Cuál es la confianza del 95% para la diferencia de mejora entre los estudiantes de álgebra introductoria y álgebra intermedia que utilizan el programa A. Las estadísticas para álgebra introductoria son media = 2.4, SD = 3.53, n = 16. Los estadísticos para álgebra intermedia son media = 4, DE = 4.89, n = 21.
Para ayudar a elegir la fórmula correcta del intervalo de confianza, observe que este problema se trata de medias pero hay dos poblaciones (estudiantes de álgebra introductoria y estudiantes de álgebra intermedia). La fórmula que cumple con estos criterios es:
(ˉxA+ˉxB±t∗(√[(nA−1)s2A+(nB−1)s2BnA+nB−2][1nA+1nB])
Hay 35 grados de libertad (nA+nB - 2). Desafortunadamente, este valor no existe sobre lat mesa del Capítulo 6, por lo que será necesario estimarlo. Un enfoque es usar el valor crítico para 30 grados de libertad (2.042) que es mayor que el valor crítico para 40 grados de libertad (2.021) ya que esto asegurará que el intervalo de confianza sea al menos tan grande como sea necesario. Después de sustituir todas las variables, la fórmula se convierte(2.4−4)±2.042(4.359√116+121) y con simplificación -1.6± 2.95. El intervalo es (-4.55,1.35). Debido a que elt∗ valor crítico es ligeramente mayor de lo que debería ser, el intervalo es ligeramente más ancho de lo que se calcularía usando las funciones en una calculadora TI 84 (-4.537,1.3368).
El segundo enfoque es encontrar este intervalo en la calculadora TI 84. Seleccione Estadísticas, Pruebas, #0 2-SampTint.
Estimación del tamaño de la muestra
La porción de margen de error de una fórmula de intervalo de confianza también se puede usar para estimar el tamaño de muestra que se necesita. Deje que E represente el margen de error deseado. Si se realiza el muestreo de datos categóricos para una población, entoncesE=z∗√ˆp(1−ˆp)n. Resuelve esto para n usando álgebra. Dado que el objetivo es asegurarse de que el tamaño de la muestra sea lo suficientemente grande, y como noˆp se conoce de antemano, entonces es necesario asegurarse de queˆp(1−ˆp) sea el mayor valor posible. Eso va a pasar cuandoˆp=0.5.
E=z∗√ˆp(1−ˆp)n
Ez∗=√ˆp(1−ˆp)n
E2z∗2=ˆp(1−ˆp)n
n=z∗2ˆp(1−ˆp)E2
n=z∗20.5(0.5)E2
n=0.25z∗2E2on=z∗24E2
Ejemplo 2
Estimar el tamaño muestral necesario para una encuesta presidencial nacional si el margen de error deseado es de 3%. Asumir 95% grado de confianza.
n=1.9624(0.03)2=1067.1o 1068 (redondear para obtener suficiente en el amplio).


