7.3: Diagramas Penrose y causalidad

No podemos visualizar directamente un colector de cuatro dimensiones. Sin embargo, cuando un espacio-tiempo tiene una simetría, es posible que podamos visualizar las propiedades relevantes de todo considerando una parte de menor dimensión del mismo. Por analogía, si quisiéramos visualizar la estructura del interior de la tierra, podríamos dibujar un diagrama que muestre una sección bidimensional a través de su centro. De hecho, podríamos deshacernos de dos dimensiones y simplemente dibujar un diagrama de una sola línea radial que va desde el núcleo de la tierra hasta su superficie; cada punto de esta línea representaría entonces una esfera. Si hacemos esto en la relatividad general, para un espacio-tiempo que es esféricamente simétrico, entonces podemos reducir el cuatridimensional a uno bidimensional, representando cada punto una biesfera. Al aplicar algunos trucos adicionales, veremos que podemos terminar con una visualización muy conveniente y útil llamada diagrama Penrose, también conocido como diagrama Penrose-Carter o diagrama causal.

Espacio-tiempo plano

Como calentamiento, la Figura 7.3.1 muestra un diagrama de Penrose para espacio-tiempo plano (Minkowski). El diagrama parece 1 + 1-dimensional, pero la convención es que se asume la simetría esférica, por lo que se ocultan dos dimensiones más, y realmente estamos retratando 3 + 1 dimensiones. Un punto típico en el interior de la región diamantada representa una esfera 2. En este tipo de diagrama, los conos de luz se ven igual que lo harían en un diagrama de espacio-tiempo normal del espacio Minkowski, pero las escalas de distancia están altamente distorsionadas. El diamante representa todo el espacio-tiempo, con la distorsión ajustando toda esta región infinita en esa área finita de la página. A pesar de la distorsión, el diagrama muestra superficies parecidas a la luz como diagonales de 45 grados. Sin embargo, las geodésicas espaciales y temporales están distorsionadas, como lo muestran las curvas del diagrama.

Figura\(\PageIndex{1}\) - Diagrama de Penrose para espacio-tiempo plano.

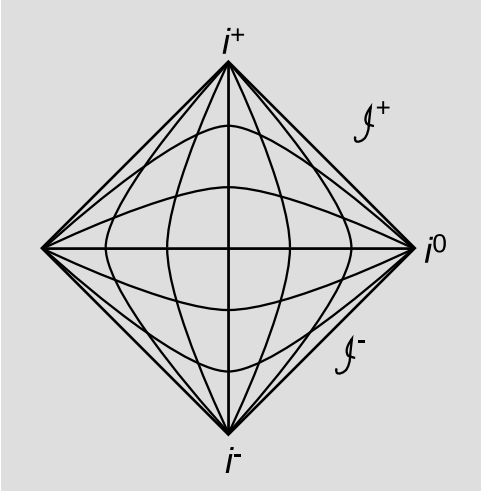
La distorsión se hace mayor a medida que nos alejamos del centro del diagrama, y se vuelve infinita cerca de los bordes. Debido a esta distorsión infinita, los puntos i ⁻ e i ⁺ en realidad representan 3 esferas. Todas las curvas temporales comienzan en i ⁻ y terminan en i ⁺, que son puntos idealizados en el infinito, como los puntos de fuga en los dibujos en perspectiva. Podemos pensar en i ⁺ como el “cementerio de elefantes”, donde van partículas masivas cuando mueren. Del mismo modo, las curvas parecidas a la luz terminan en\(\mathscr{I}^{+}\) (que incluye su imagen especular a la izquierda), denominadas infinito nulo. ³ El punto en i ⁰ es un punto final infinitamente distante para curvas espaciales. Debido a la simetría esférica, las mitades izquierda y derecha del diagrama son redundantes.

Es posible inventar fórmulas explícitas que se traducen de ida y vuelta entre las coordenadas de Minkowski y los puntos sobre el diamante, pero en general esto no es necesario. De hecho, la utilidad de los diagramas es que nos dejan pensar en las relaciones causales de manera independiente de coordenadas. Un cono de luz en el diagrama se ve exactamente como un cono de luz normal.

Dado que este espacio-tiempo en particular es homogéneo, no hace diferencia qué ubicación espacial en el diagrama escogemos como nuestro eje de simetría. Por ejemplo, podríamos elegir arbitrariamente la esquina izquierda, la geodésica central parecida al tiempo (dibujada recta) o una de las otras geodésicas similares al tiempo (representadas como si fueran curvas).

Schwarzschild Espacio-tiempo

La Figura 7.3.2 es un diagrama de Penrose para el espacio-tiempo Schwarzschild, es decir, un espacio-tiempo que se parece al espacio Minkowski, excepto que tiene un agujero negro eterno en él. Se trata de un agujero negro que no se formó por colapso gravitacional. Este espacio-tiempo no es homogéneo; tiene una ubicación específica que es su centro de simetría esférica, y esta es la línea vertical de la izquierda marcada con r = 0. El triángulo es el espacio-tiempo dentro del horizonte de eventos; podríamos haberlo copiado a través de la línea r = 0 si así lo hubiéramos deseado, pero las copias habrían sido redundantes.

Figura\(\PageIndex{2}\) - Diagrama de Penrose para el espacio-tiempo Schwarzschild: un agujero negro que no se formó por colapso gravitacional.

El diagrama de Penrose facilita razonar sobre las relaciones causales. Por ejemplo, podemos ver que si una partícula alcanza un punto dentro del horizonte de eventos, todo su futuro causal se encuentra dentro del horizonte, y todas sus posibles líneas mundiales futuras se cruzan con la singularidad. El horizonte es una superficie parecida a la luz, lo cual tiene sentido, porque se define como el límite del conjunto de puntos desde los que podría llegar un rayo de luz\(\mathscr{I}^{+}\).

Agujero Negro Astrofísico

La Figura 7.3.3 es un diagrama de Penrose para un agujero negro que se ha formado por colapso gravitacional. Usando este tipo de diagrama, podemos abordar sucintamente una de las preguntas frecuentes más molestas sobre los agujeros negros. (Cf. Sección 6.3, donde tomamos un enfoque más engorroso sin diagramas Penrose.) Si un observador distante observa la nube colapsada de materia a partir de la cual se forma el agujero negro, sus observaciones ópticas mostrarán que la luz de la materia se vuelve cada vez más desplazada al rojo gravitacionalmente, y si lo desea, puede interpretarlo como un ejemplo de dilatación gravitacional del tiempo. A medida que espera cada vez más, las señales de luz de la materia infalible tardan cada vez más en llegar. El desplazamiento al rojo se acerca al infinito a medida que la materia se acerca al horizonte, por lo que las ondas de luz finalmente se vuelven demasiado bajas en energía para ser detectables por cualquier instrumento dado. Además, su paciencia (o su vida) se agotará, porque el tiempo en su reloj se acerca al infinito mientras espera recibir señales de la materia que se acerca al horizonte. Todo esto es exactamente como debería ser, ya que el horizonte es por definición el límite de su universo observable. (Un rayo de luz emitido desde el horizonte terminará en i ⁺, que es un punto final de líneas mundiales similares al tiempo alcanzadas solo por observadores que han experimentado una cantidad infinita de tiempo adecuado).

Figura\(\PageIndex{3}\) - Diagrama de Penrose para un agujero negro formado por colapso gravitacional.

Las personas a las que les molestan estos temas a menudo reconocen la inobservabilidad externa de la materia que pasa por el horizonte, y luego quieren pasar de esto a preguntas como: “¿Eso significa que el agujero negro nunca se forma realmente?” Esto presupone que nuestro observador distante tiene una noción de simultaneidad singularmente definida que se aplica a una región del espacio que se extiende desde su propia posición hasta el interior del agujero negro, para que pueda decir lo que sucede dentro del agujero negro “ahora”. Pero la noción de simultaneidad en la relatividad general es aún más limitada que su contraparte en la relatividad especial. No sólo la simultaneidad en la relatividad general depende del observador, como en la relatividad especial, sino que también es local más que global.

En la Figura 7.3.4, E es un evento en la línea mundial de un observador. La superficie espacial _S1 es una posible “ahora” para este observador. Según esta superficie, ninguna partícula ha caído jamás y llegado al horizonte; cada partícula de este tipo tiene una línea mundial que se cruza con _S1, y por lo tanto todavía está en camino.

Figura\(\PageIndex{4}\) - Según el observador distante, ¿la materia infalible llega alguna vez a la singularidad?

S ₂ es otro posible “ahora” para el mismo observador al mismo tiempo. Según esta definición de “ahora”, todas las partículas han pasado por el horizonte de eventos, pero ninguna ha alcanzado todavía la singularidad. Por último, S ₃ es un “ahora” según el cual todas las partículas han golpeado la singularidad.

Si se trataba de una relatividad especial, entonces podríamos decidir qué superficie era la noción correcta de simultaneidad para el observador, a partir del estado de movimiento del observador. Pero en la relatividad general, esto sólo funciona localmente (razón por la cual hice que las tres superficies coincidieran cerca de E). No hay una forma bien definida de decidir cuál es la forma correcta de extender globalmente esta noción de simultaneidad.

Si bien puede parecer extraño que no podamos decir si la singularidad “ya” se ha formado según un observador distante, esto es realmente solo un resultado inevitable del hecho de que la singularidad es espacial. Lo mismo sucede en el caso de un espacio-tiempo Schwarzschild, que consideramos como una descripción de un eterno agujero negro, es decir, uno que siempre ha existido y siempre lo hará. En el diagrama similar de Penrose para un agujero negro eterno, todavía podemos dibujar una superficie espacial como S ₁ o S ₂, representando una definición de “ahora” tal que la singularidad aún no existe.

Diagramas Penrose en General

Idealmente nos gustaría generalizar el procedimiento para dibujar diagramas Penrose para poder determinar de manera única uno para cualquier espacio-tiempo. Esto resulta no ser tan claro. El procedimiento sería algo como esto:

1. Hacer una sección o proyección n-dimensional, donde generalmente, pero no siempre, n = 2.
2. Hacer una transformación para reducir el colector resultante a uno plano de tamaño finito.
3. Colinda con superficies idealizadas y apunta al infinito.

En el paso 1, queremos aprovechar cualquier simetría, como la simetría rotacional, para que el resultado final sea informativo, sea representativo de todo el espacio-tiempo y represente con precisión las relaciones causales en el espacio-tiempo original. Si el espacio-tiempo original tiene un bajo grado de simetría (por ejemplo, un espacio-tiempo que contiene tres agujeros negros dispuestos en un triángulo), entonces esto podría requerir n > 2. En este paso también necesitamos asegurarnos de que las geodésicas similares a la luz en el espacio original corresponden correctamente a las geodésicas similares a la luz en el subcolector.

Para el paso 2, ya hemos dado una caracterización geométrica del tipo de transformación que tenemos en mente, lo que se denomina transformación conforme. Resulta posible encapsular esta idea de una manera analítica sencilla. Dado un espacio-tiempo con una métrica g, definimos una métrica ficticia\(\tilde{g} = \Omega^{2} g\), donde\(\Omega\) es un número real distinto de cero que varía de un punto a otro. (Cf. sec. 5.11, donde\(\Omega\) fue constante.) La idea aquí es que g y\(\tilde{g}\) estén de acuerdo en dónde está el cono de luz, pero no están de acuerdo en la medición de distancias y tiempos. El mismo colector equipado con la métrica ficticia\(\tilde{g}\) es el que se dibuja en la página cuando hacemos un diagrama de Penrose. Dejamos\(\Omega\) → 0 a medida que nos acercamos a las regiones limítrofes idealizadas como i ⁰ y\(\mathscr{I}^{+}\), y esto es lo que hace que el diagrama de Penrose ocupe espacio finito en la página.

No es posible en general hacer lo que se requiere en el paso 2 haciendo una transformación conforme para cambiar un colector en uno plano. Un colector que se puede aplanar de esta manera se denomina conformalmente plano. Todos los colectores bidimensionales son conformalmente planos, por lo que en el caso n = 2 esto está garantizado. Para n > 3 normalmente no tendremos planitud conforme si hay ondas gravitacionales o fuerzas mareales presentes.

La parte más problemática, sorprendentemente, es el paso 3. Este tema va bajo el rubro general de “construcciones de límites”. Hay reseñas disponibles sobre este tema. ⁴ Hay una serie de técnicas más o menos específicas para construir un límite, con una sopa de alfabeto de nombres que incluyen el límite g, el límite c, el límite b y el límite a. Como alguien que no es especialista en este subcampo, la impresión que me da es que se trata de un área de investigación que ha resultado mal y nunca ha producido ningún resultado útil, pero el trabajo continúa, y es posible que en algún momento el humo se despeje. Como ejemplo sencillo de lo que a uno le gustaría obtener, pero no se obtiene, de estos estudios, parecería natural preguntarse cuántas dimensiones hay en una singularidad de agujero negro. (Véase el ejemplo 4 para una discusión de por qué se trata de una pregunta no trivial.) Diferentes respuestas regresan de los diferentes métodos. Por ejemplo, el enfoque b-boundary dice que tanto las singularidades de agujero negro como las cosmológicas son puntos de dimensión cero, mientras que en el método c-boundary (que fue diseñado para armonizar con los diagramas de Penrose) son de tres superficies (como se imaginaría a partir de los diagramas de Penrose).

Hiperbolicidad Global

La causalidad se refiere a nuestro sentimiento vagamente definido de que el mundo debe tener una progresión ordenada de causa y efecto. Hacer esta noción más precisa es sorprendentemente difícil. Los diagramas de Penrose, y sus conceptos asociados, son esencialmente representaciones de la estructura causal del espacio-tiempo, y estos resultan ser útiles para armar uno de los intentos más satisfactorios de definir la causalidad. Esta definición se llama hiperbolicidad global. La terminología oscura se relaciona con la clasificación de ecuaciones diferenciales parciales.

Algunas definiciones se requieren como preliminares. Considera un conjunto S de eventos en el espacio-tiempo. S está acotada si no incluye ninguno de los puntos idealizados en el diagrama de Penrose que hemos agregado en el infinito. ⁵ S está cerrado si contiene su propio límite. ⁶ S es compacto si está cerrado y acotado.

Notas

⁵ Más rigurosamente, esto equivale a decir que para cualquier geodésico en S, hay un límite en el parámetro afín.

⁶ Para hacerlo más preciso, procedemos como se describe en la sección 5.10 ampliando el conjunto de puntos en nuestro colector espacio-temporal M para incluir puntos a distancias infinitesimales de uno de los puntos originales. Entonces S se cierra si, para cualquier punto en la versión ampliada de S, hay un punto que se encuentra a una distancia infinitesimal de él en la versión original de S.

Ejemplo 9: Conos ligeros compactos y no compactos

La Figura 7.3.5 muestra un espacio-tiempo que contiene un agujero negro que se forma por colapso gravitacional. El punto P está dentro del horizonte de eventos, Q afuera. Considere los siguientes cuatro conjuntos de puntos:

Figura\(\PageIndex{5}\)

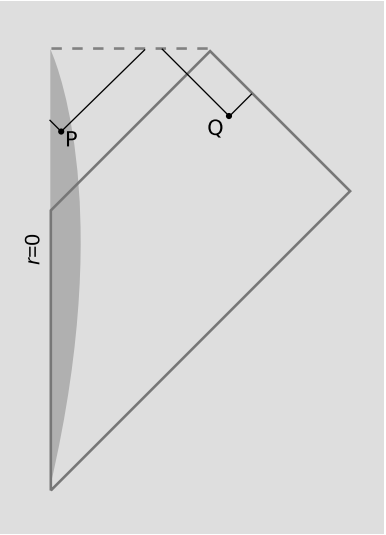
I ⁺ (P), llamado el futuro cronológico de P, es el interior del cono de luz dirigido al futuro de P.

J ⁺ (P) es como I ⁺ (P), pero también incluye eventos que están en el límite del cono de luz, es decir, eventos que no pueden conectarse a P por una curva similar al tiempo pero que pueden conectarse a él por una curva similar a la luz. A esto lo llamamos el futuro causal de P, ya que es el conjunto de eventos que podría ocasionar P.

I ⁺ (Q) y J ⁺ (Q) son los conjuntos análogos construidos sobre Q.

De estos cuatro conjuntos, solo J ⁺ (P) es compacto. I ⁺ (P) no es compacto porque no está cerrado. I ⁺ (Q) y J ⁺ (Q) no son compactos porque no están acotados; incluyen puntos idealizados en el infinito que se encuentran en i ⁺ y\(\mathscr{I}^{+}\).

Además de la notación introducida en el ejemplo 9, necesitaremos las notaciones similares I ⁻ y J ⁻ para los conos de luz pasados correspondientes.

Definición

Un espacio-tiempo es globalmente hiperbólico si: (1) no hay curvas cerradas, similares al tiempo (CTC), ⁷ y (2) dados dos eventos P y Q cualesquiera, la intersección de J ⁺ (P) y J ⁻ (Q) es compacta. (La condición 2 solo se requiere cuando P y Q son puntos en el colector, no puntos de límite).

---

⁷ Para mayor precisión, la condición necesita ser un poco más fuerte. No queremos curvas cerradas, no espaciales, y también queremos que sea imposible que existan curvas que estén arbitrariamente cercanas a ser tales curvas, en el sentido de que para cualquier evento, existe un vecindario a su alrededor que nunca podrá ser revisitado.

En un espacio-tiempo globalmente hiperbólico, los problemas de valor inicial siempre tienen soluciones únicas. Es decir, podemos elegir una superficie espacial y dar el valor de una ola en esa superficie, y la ecuación de onda tendrá entonces una solución única. Tal superficie se llama superficie Cauchy.

Podemos verificar fácilmente mediante la inspección de los digramas de Penrose que los espacio-tiempos descritos anteriormente en esta sección son globalmente hiperbólicos. La condición 2 implica que la intersección no contiene singularidades ni puntos al infinito. Si bien los espacio-tiempos del agujero negro sí contienen singularidades, la naturaleza espacial de estas singularidades implica que nunca podrán estar en la intersección de los conos de luz como se menciona en la definición. Por lo tanto, tales espacio-tiempos son globalmente hiperbólicos.

Ejemplo 10: Hiperbolicidad global

Figura\(\PageIndex{6}\)

La Figura 7.3.6 (1) muestra una pieza cortada del espacio Minkowski. El contorno discontinuas está destinado a indicar que la pieza no incluye su límite. Este espacio-tiempo no es globalmente hiperbólico. Para ciertas elecciones de eventos P y Q, la intersección J ⁺ (P) J ⁻ (Q) podría extenderse hasta el corte en el borde. Dado que el espacio-tiempo no incluye su límite, esta intersección no sería compacta. Es fácil ver por qué falla la causalidad en este espacio-tiempo. Si elegimos una superficie similar al espacio cerca de la parte inferior del diagrama, solo cortaría una pequeña parte del fondo del espacio-tiempo. En tiempos posteriores, el espacio-tiempo crece a un ritmo que es mayor que c. Por lo tanto, tal superficie no puede ser utilizada como superficie Cauchy; dadas las condiciones iniciales en esta superficie, no podemos predecir lo que sucederá en las partes del universo que están fuera de su futuro causal.

En la Figura 7.3.6 (2) tenemos el mismo ejemplo, pero ahora se incluye el límite. Este conjunto no es un colector, lo que lo excluye de la consideración como espacio-tiempo en la relatividad general. La Figura 7.3.6 (3) es una imagen del espacio Minkowski con una singularidad similar al tiempo en él (línea discontinua). Las singularidades no son conjuntos de puntos en el colector, por lo que topológicamente, esto es como el espacio Minkowski con una sola curva similar al tiempo extirpada quirúrgicamente. La hiperbolicidad global falla porque la intersección J ⁺ (P) J ⁻ (Q) podría rodear la singularidad, y no sería compacta porque no incluiría su límite en la singularidad. Esta violación de la hiperbolicidad global indica una falla de causalidad en dicho espacio-tiempo (ver sección 6.3).

Al cortar la mitad inferior del diamante que representa el espacio-tiempo Minkowski, se obtiene la Figura 7.3.6 (4). La línea discontinua indica que el límite no está incluido, y por lo tanto este es un colector. También es globalmente hiperbólico. Este ejemplo sugiere que la hiperbolicidad global no necesariamente captura todo lo que podríamos querer describir en una definición de causalidad. Si una paleontóloga que vive en este espacio-tiempo encuentra un fósil de dinosaurio incrustado en una roca, naturalmente inferirá que un dinosaurio vivió en algún momento del pasado, haciendo que el fósil exista. Pero quizás este no es el caso —el hipotético dinosaurio podría ser uno que hubiera existido antes del límite. Esta violación de causalidad con sabor a creacionismo es de un sabor diferente al de la situación que hubiéramos tenido si el borde inferior del diagrama hubiera sido una singularidad del big bang; en ese caso, habríamos tenido una razón cognoscible por la que las cadenas de causa y efecto no podrían extenderse de nuevo al pasado más allá de un cierto tiempo.

Referencias

³ Véase también la sección 7.4

⁴ Ashley, “Teoremas de la singularidad y la construcción de límites abstractos”, digitalcollections.anu.edu.a... dle/1885/46055. GarciaParrado y Senovilla, “Estructuras causales y límites causales”, http://arxiv.org/abs/gr-qc/0501069.