3.19: Amplificadores Operacionales
- Page ID
- 85560
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Una breve descripción del funcionamiento de un amplificador operacional.
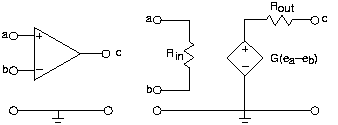
Los amplificadores operacionales no solo tienen el modelo de circuito que se muestra en la Figura 3.19.1 anterior, sino que sus valores de elementos son muy especiales.
- La resistencia de entrada, R in, es típicamente grande, del orden de 1 MΩ.
- La resistencia de salida, R out, es pequeña, generalmente inferior a 100 Ω.
- La ganancia de voltaje, G, es grande, superior a 10 5.
La gran ganancia llama la atención; sugiere que un amplificador operacional podría convertir una señal de entrada de 1 mV en una de 100 V. Si tuviera que construir un circuito de este tipo, conectar una fuente de voltaje al nodo a, conectar el nodo b a la referencia y mirar la salida, se sentiría decepcionado. Al tratar con componentes electrónicos, no se puede olvidar la fuente de alimentación no representada pero necesaria.
Es imposible que los componentes electrónicos produzcan voltajes que excedan los proporcionados por la fuente de alimentación o que produzcan corrientes que excedan la clasificación de la fuente de alimentación.
Los voltajes de fuente de alimentación típicos requeridos para los circuitos de amplificador operacional son + (15V). Adjuntar la señal de 1 mv no solo fallaría en producir una señal de 100 V, la forma de onda resultante estaría severamente distorsionada. Si bien es un resultado deseable si eres un aficionado al rock & roll, los estéreos de alta calidad no deben distorsionar las señales. Otra consideración al diseñar circuitos con amplificadores operacionales es que estos valores de elementos son típicos: El control cuidadoso de la ganancia solo se puede obtener eligiendo un circuito para que sus valores de elementos dicten la ganancia resultante, que debe ser menor que la proporcionada por el amplificador operacional.
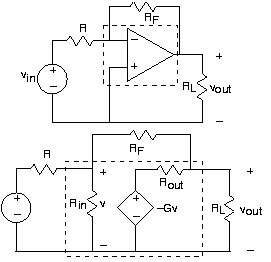
Amplificador de inversión
La configuración de retroalimentación mostrada en la Figura 3.19.2 es el circuito de amplificador operacional más común para obtener lo que se conoce como amplificador inversor.
\[\left ( \frac{R_{F}R_{out}}{R_{out}-GR_{F}}\left ( \frac{1}{R_{out}}+\frac{1}{R_{in}}+\frac{1}{R_{L}}\right )\left ( \frac{1}{R}+\frac{1}{R_{in}}+\frac{1}{R_{F}} \right ) -\frac{1}{R_{F}} \right )v_{out}=\frac{1}{R}v_{in} \nonumber \]
proporciona la relación exacta de entrada y salida. Al elegir los valores de los elementos con respecto a las características op-amp, podemos simplificar drásticamente la expresión.
- Hacer que la resistencia de carga, R L, sea mucho mayor que la salida R. Esta situación baja el término 1/R L del segundo factor de la ecuación anterior.
- Hacer que la resistencia, R, sea menor que R in, lo que significa que el 1/R en término en el tercer factor es despreciable.
Con estos dos criterios de diseño, la expresión se convierte en:
\[\left ( \frac{R_{F}R_{out}}{R_{out}-GR_{F}}\left ( \frac{1}{R}+\frac{1}{R_{F}} \right ) -\frac{1}{R_{F}} \right )v_{out}=\frac{1}{R}v_{in} \nonumber \]
Debido a que la ganancia es grande y la resistencia R out es pequeña, el primer término se convierte en -1/G, dejándonos con:
\[\left ( \left ( -\frac{1}{G} \right )\left ( \frac{1}{R}+\frac{1}{R_{F}} \right ) -\frac{1}{R_{F}} \right )v_{out}=\frac{1}{R}v_{in} \nonumber \]
Si seleccionamos los valores de R F y R para que GR>>R F, este factor ya no dependerá de la ganancia inherente del op-amp, y será igual a -1/R F. Bajo estas condiciones, se obtiene la relación clásica entrada-salida para el amplificador inversor basado en op-amp.
\[v_{out}=-\left ( \frac{R_{F}}{R}v_{in} \right ) \nonumber \]
En consecuencia, la ganancia proporcionada por nuestro circuito está totalmente determinada por nuestra elección de la resistencia de retroalimentación R F y la resistencia de entrada R. Siempre es negativa, y puede ser menor de uno o mayor que uno en magnitud. No puede exceder la ganancia inherente del amplificador operacional y no debe producir salidas tan grandes que resulten distorsiones (¡recuerde la fuente de alimentación!). Curiosamente, tenga en cuenta que esta relación no depende de la resistencia de carga. Este efecto se produce porque utilizamos resistencias de carga grandes en comparación con la resistencia de salida del amplificador operacional. Por lo tanto, la observación significa que, si es cuidadoso, podemos colocar circuitos de amplificador operacional en cascada, sin incurrir en el efecto de circuitos sucesivos cambiando el comportamiento (función de transferencia) de los anteriores; vea este problema.
Filtros activos
Siempre y cuando se cumplan los requisitos de diseño, la relación entrada-salida para el amplificador inversor también se aplica cuando los elementos del circuito de retroalimentación y entrada son impedancias (resistencias, condensadores e inductores).
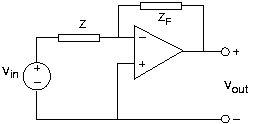
\[\frac{V_{out}}{V_{in}}=-\frac{Z_{F}}{Z} \nonumber \]
Diseñemos un circuito de amplificador operacional que funcione como un filtro de paso bajo. Queremos que la función de transferencia entre la salida y la tensión de entrada sea:
\[H(f)=\frac{K}{1+\frac{if}{f_{c}}} \nonumber \]
donde K es igual a la ganancia de banda de paso y f c es la frecuencia de corte. Supongamos que la inversión (ganancia negativa) no importa. Con la función de transferencia del circuito op-amp anterior en mente, consideremos algunas opciones.
- \[Z_{F}=K,\; \; Z=1+\frac{if}{f_{c}} \nonumber \]
Esta elección significa que la impedancia de retroalimentación es una resistencia y que la impedancia de entrada es una combinación en serie de un inductor y una resistencia. En el diseño de circuitos, tratamos de evitar los inductores porque son físicamente más voluminosos que los condensadores.
- \[Z_{F}=\frac{1}{1+\frac{if}{f_{c}}},\; \; Z=\frac{1}{K} \nonumber \]
Considere el recíproco de la impedancia de retroalimentación (su admitancia):
\[Z_{F}^{-1}=1+\frac{if}{f_{c}} \nonumber \]
Dado que esta admitancia es una suma de admitancias, esta expresión sugiere la combinación paralela de una resistencia (valor = 1 Ω) y un condensador (valor =( 1/f c) F). Tenemos la idea correcta, pero los valores (como 1 Ω) no son correctos. Considere la combinación paralela RC general; su admisión es
\[\frac{1}{R_{F}}+i2\pi fC \nonumber \]
Dejando que la resistencia de entrada sea igual a R, la función de transferencia del amplificador inversor op-amp ahora es
\[H(f)=-\frac{\frac{R_{F}}{R}}{1+i2\pi fR_{F}C} \nonumber \]
donde la ganancia es igual
\[\frac{R_{F}}{R} \nonumber \]
y la frecuencia de corte
\[\frac{1}{R_{F}C} \nonumber \]
Crear una función de transferencia específica con amplificadores operacionales no tiene una respuesta única. A diferencia del diseño con circuitos pasivos, la electrónica es más flexible (se puede construir una cascada de circuitos para que cada uno tenga poco efecto en los demás; ver [enlace]) y puede resultar ganancia (aumento de potencia y amplitud). Para completar nuestro ejemplo, supongamos que queremos un filtro de paso bajo que emule lo que hacen las compañías telefónicas. Las señales transmitidas por teléfono tienen un límite de frecuencia superior de aproximadamente 3 kHz. Para la segunda opción de diseño, requerimos R F C=5.3x10 -5. Por lo tanto, son posibles muchas opciones para los valores de resistencia y capacitancia. Un condensador de 1 μF y una resistencia de 330 Ω, 10 nF y 33 kΩ, y 10 pF y 33 MΩ funcionarían teóricamente. También deseemos una ganancia de voltaje de diez:
\[\frac{R_{F}}{R}=10 \nonumber \]
\[R=\frac{R_{F}}{10} \nonumber \]
Recordemos que debemos tener R<R en.
Como la impedancia de entrada del amplificador operacional es de aproximadamente 1 MΩ, no queremos
\[\frac{\left | Z_{F} \right |}{R}< 10^{5} \nonumber \]
para todas las frecuencias de interés. Por lo tanto,
\[\frac{\frac{R_{F}}{\left | 1+i2\pi fR_{F}C \right |}}{R}< 10^{5} \nonumber \]
A medida que esta impedancia disminuye con la frecuencia, la especificación de diseño de
\[\frac{R_{F}}{R}=10 \nonumber \]
significa que este criterio se cumple fácilmente. Por lo tanto, las dos primeras opciones para los valores de resistencia y condensador (así como muchas otras en este rango) funcionarán bien. Consideraciones adicionales como el costo de las piezas podrían entrar en la imagen. A menos que tenga una aplicación de alta potencia (esta no es una) o pida componentes de alta precisión, los costos no dependen en gran medida de los valores de los componentes siempre que se mantenga cerca de los valores estándar. Para resistencias, que tienen valores r10 d, se obtienen fácilmente valores de
Qué tienen de especial los valores de resistencia; ¿por qué estos valores de apariencia bastante impar para r?
Solución
La relación entre los valores adyacentes es aproximadamente\[\sqrt{2} \nonumber \]
Manera intuitiva de resolver circuitos Op-Amp
Cuando cumplimos con las especificaciones de diseño de amplificador operacional, podemos simplificar enormemente nuestros cálculos de circuitos, tanto que no necesitamos el modelo de circuito del amplificador operacional para determinar la función de transferencia. Aquí está nuestro amplificador inversor.
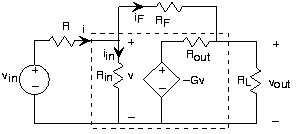
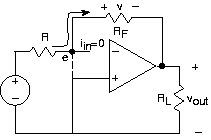
Cuando aprovechamos las características del amplificador operacional (gran impedancia de entrada, gran ganancia y pequeña impedancia de salida), observamos los dos hechos importantes siguientes.
- El i in actual debe ser muy pequeño. El voltaje producido por la fuente dependiente es 10 5 veces el voltaje v. Por lo tanto, el voltaje
- Debido a esta suposición, esencialmente no hay flujo de corriente a través de R en el voltaje
Armados con estas aproximaciones, volvamos a nuestro circuito original como se muestra en la Figura 3.19.4. El voltaje del nodo e es esencialmente cero, lo que significa que está esencialmente vinculado al nodo de referencia. Así, la corriente a través de la resistencia R es:
\[i=\frac{v_{in}}{R} \nonumber \]
Además, la resistencia de realimentación aparece en paralelo con la resistencia de carga. Debido a que la corriente que entra en el amplificador operacional es cero, ¡toda la corriente que fluye a través de R fluye a través de la resistencia de retroalimentación (i F = i)! El voltaje a través de la resistencia de retroalimentación R es igual a:
\[v=\frac{v_{in}R_{F}}{R} \nonumber \]
Debido a que el extremo izquierdo de la resistencia de retroalimentación está esencialmente unido al nodo de referencia, el voltaje a través de él es igual al negativo de eso a través de la resistencia de salida:
\[v_{out}=-v=-\frac{v_{in}R_{F}}{R} \nonumber \]
El uso de este enfoque facilita mucho el análisis de nuevos circuitos de amplificador operacional. Al usar esta técnica, verifique para asegurarse de que los resultados que obtiene sean consistentes con los supuestos de que esencialmente una corriente cero ingresa al amplificador operacional y un voltaje casi cero a través de las entradas del amplificador operacional.
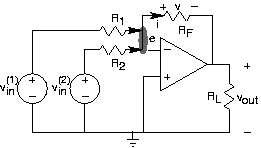
Intentemos esta técnica de análisis sobre una simple extensión de la configuración del amplificador inversor que se muestra en la Figura 3.19.5 anterior. Si alguna de las combinaciones fuente-resistencia no estuviera presente, el amplificador inversor permanece, y sabemos que la función de transferencia. Por superposición, sabemos que la relación entrada-salida es:
\[v_{out}=\left ( -\left ( \frac{R_{F}}{R_{1}} v_{in}^{(1)}\right ) \right )-\frac{R_{F}}{R_{2}} v_{in}^{(2)} \nonumber \]
Cuando partimos de cero, el nodo que une las tres resistencias está al mismo potencial que la referencia,
\[e\simeq 0 \nonumber \]
La suma de corrientes que fluyen hacia ese nodo es cero. Por lo tanto, la corriente i que fluye en la resistencia R F es igual a:
\[i=\frac{v_{in}^{(1)}}{R_{1}}+\frac{v_{in}^{(2)}}{R_{2}} \nonumber \]
Debido a que la resistencia de retroalimentación está esencialmente en paralelo con la resistencia de carga, los voltajes deben satisfacer
\[v=-v_{out} \nonumber \]
De esta manera, obtenemos la relación input-output dada anteriormente.
¿Qué utilidad tiene este circuito? ¿Se puede extender sin límite la noción básica del circuito?


