3.20: El Diodo

Objetivos de aprendizaje

• Una breve descripción de un diodo y su funcionamiento interno.

Figura 3.20.1 relación v-i y símbolo esquemático para el diodo. Aquí, los parámetros del diodo fueron temperatura ambiente y I ₀ =1μA

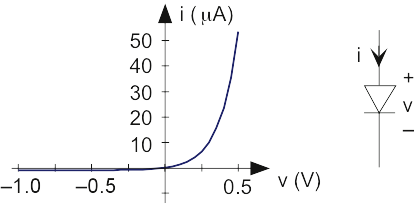
La resistencia, el condensador y el inductor son elementos de circuito lineal en que sus relaciones v-i son lineales en el sentido matemático. Las fuentes de voltaje y corriente son (técnicamente) dispositivos no lineales: dicho simplemente, duplicar la corriente a través de una fuente de voltaje no duplica la tensión. Un elemento de circuito no lineal más descarado y muy útil es el diodo (aprende más). Su relación insumo-producto tiene una forma exponencial.

\[i(t)=I_{0}\left ( e^{\frac{q}{kT}v(t)} -1\right ) \nonumber \]

Aquí, la cantidad q representa la carga de un solo electrón en culombios, k es la constante de Boltzmann y T es la temperatura del diodo en K. A temperatura ambiente, la relación

\[\frac{kT}{q}=25mV \nonumber \]

La constante I ₀ es la corriente de fuga, y suele ser muy pequeña. Al ver esta relación v-i en la Figura 3.20.1, la no linealidad se vuelve obvia. Cuando el voltaje es positivo, la corriente fluye fácilmente a través del diodo. Esta situación se conoce como sesgo hacia adelante. Cuando aplicamos un voltaje negativo, la corriente es bastante pequeña, e igual a I ₀, conocida como la corriente de fuga o polarización inversa. Un modelo menos detallado para el diodo tiene cualquier corriente positiva que fluye a través del diodo cuando está polarizado hacia delante, y ninguna corriente cuando está polarizado negativamente. Tenga en cuenta que el símbolo esquemático del diodo parece una punta de flecha; la dirección del flujo de corriente corresponde a la dirección que apunta la punta de flecha.

Figura 3.20.2 El circuito de diodos

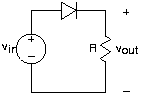
Debido a la naturaleza no lineal del diodo, no podemos usar impedancias ni reglas de combinación serie/paralelo para analizar los circuitos que los contienen. El método de nodo confiable siempre se puede usar; solo se basa en KVL para su aplicación, y KVL es una declaración sobre caídas de voltaje alrededor de una ruta cerrada independientemente de si los elementos son lineales o no. Así, para este sencillo circuito tenemos

\[\frac{v_{out}}{R}=I_{0}\left ( e^{\frac{q}{kT}(v_{m}-v_{out})} -1\right ) \nonumber \]

Esta ecuación no se puede resolver en forma cerrada. Debemos entender lo que está pasando desde principios básicos, utilizando ayudas computacionales y gráficas. Como aproximación, cuando v _in es positivo, la corriente fluye a través del diodo siempre que el voltaje v _out sea menor que v _in (por lo que el diodo está polarizado hacia adelante). Si la fuente es negativa o v _out “intenta” ser más grande que v _en el diodo es polarizado inverso, y la corriente de polarización inversa fluye a través del diodo. Así, en este nivel de análisis, los voltajes de entrada positivos dan como resultado voltajes de salida positivos con negativos dando como resultado:

\[v_{out}=-(RI_{0}) \nonumber \]

Figura 3.20.3 Gráficas de corriente y voltaje de diodo

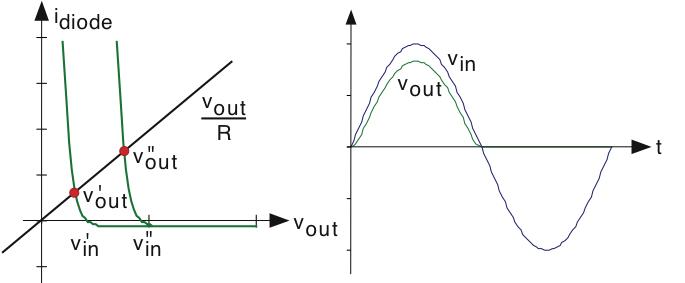
Necesitamos detallar la no linealidad exponencial para determinar cómo el circuito distorsiona la forma de onda del voltaje de entrada. Por supuesto, podemos resolver numéricamente la Figura 3.20.2 para determinar el voltaje de salida cuando la entrada es una sinusoide. Para saber más, expresemos esta ecuación gráficamente. Trazamos cada término como una función de v _out para diversos valores del voltaje de entrada v _en donde se cruzan nos da el voltaje de salida. El lado izquierdo, la corriente a través de la resistencia de salida, no varía por sí mismo con v _in, y así tenemos una línea recta fija. En cuanto al lado derecho, que expresa la relación v-i del diodo, el punto en el que la curva cruza el eje v _out nos da el valor de v _in. Claramente, las dos curvas siempre se cruzarán solo una vez para cualquier valor de v _in, y para v positivo _en la intersección ocurre a un valor para v _out menor que v _pulg. Esta reducción es menor si la línea recta tiene una pendiente menos profunda, lo que corresponde a usar una resistencia de salida más grande. Para v _in negativo, el diodo es polarizado inverso y el voltaje de salida es igual a:

\[v_{out}=-(RI_{0}) \nonumber \]

¿Qué utilidad podría tener este sencillo circuito? La no linealidad del diodo no se puede escapar aquí, y la distorsión claramente evidente debe tener alguna aplicación práctica si el circuito fuera útil. Este circuito, conocido como rectificador de media onda, está presente en prácticamente todas las radios AM dos veces y ¡cada uno sirve funciones muy diferentes! Aprenderemos qué funciona más adelante.

Figura 3.20.4 Rectificador de media onda

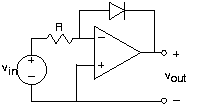
Aquí hay un circuito que involucra a un diodo que en realidad es más sencillo de analizar que el anterior. Sabemos que la corriente a través de la resistencia debe ser igual a la que pasa por el diodo. Así, la corriente del diodo es proporcional a la tensión de entrada. Como el voltaje a través del diodo está relacionado con el logaritmo de su corriente, vemos que la relación entrada-salida es:

\[v_{out}=-\left ( \frac{kT}{q} \ln \left ( \frac{v_{in}}{RI_{0}}+1 \right )\right ) \nonumber \]

Claramente, el nombre amplificador logarítmico está justificado para este circuito.