10.8: Patrón de radiación
- Page ID
- 83691
El patrón de radiación de una antena transmisora describe la magnitud y polarización del campo radiado por la antena en función del ángulo relativo a la antena. También se puede definir un patrón para una antena receptora, sin embargo, diferimos la discusión del caso de recepción a una sección posterior.
El concepto de patrón de radiación está estrechamente relacionado con los conceptos de directividad y ganancia (Sección 10.7). La principal distinción es la consideración explícita de la polarización. En muchas aplicaciones, la polarización del campo irradiado por una antena transmisora es tan importante como la densidad de potencia radiada por la antena. Por ejemplo, un enlace de radiocomunicación consiste en una antena que está transmitiendo separada por cierta distancia de una antena que está recibiendo. La directividad determina la densidad de potencia entregada a la antena receptora, pero la antena receptora debe estar copolarizada con la onda que llega para capturar toda esta potencia.
El concepto de patrón de radiación se explica quizás mejor con el ejemplo. La antena más simple que se encuentra en la práctica común es el dipolo eléctrico corto (ESD), que consiste en un cable recto de longitud\(L\) que es mucho menor que la mitad de una longitud de onda. En la Sección 9.5, se muestra que el campo irradiado por un ESD que se ubica en el origen y alineado a lo largo del\(z\) eje es:
\[\widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} j \eta \frac{I_0\cdot\beta L}{8\pi} ~\left(\sin\theta\right) ~\frac{e^{-j\beta r}}{r} \label{m0205_eESDE} \]
donde\(I_0\) representa la magnitud y fase de la corriente aplicada a los terminales,\(\eta\) es la impedancia de onda del medio, y\(\beta=2\pi/\lambda\) es la constante de propagación de fase del medio. Tenga en cuenta que la dirección de referencia del campo eléctrico está en la\(\hat{\bf \theta}\) dirección; por lo tanto, un receptor debe estar\(\hat{\bf \theta}\) polarizado en relación con el sistema de coordenadas del transmisor para capturar toda la potencia disponible. Un receptor que no esté completamente\(\hat{\bf \theta}\) polarizado capturará menos energía. En el extremo, un receptor\(\hat{\bf \phi}\) polarizado con respecto al sistema de coordenadas del transmisor capturará potencia cero. Así, para la ESD\(\hat{\bf z}\) orientada, nos referimos a la\(\hat{\bf \theta}\) polarización del campo transmitido como “co-polarizada” o simplemente “co-pol”, y la\(\hat{\bf \phi}\) -polarización del campo transmitido como “cross-pol”.
En este punto, el lector puede preguntarse a qué propósito sirve definir la polarización cruzada, ya que la definición dada anteriormente parece sugerir que el cross-pol siempre debe ser cero. En la práctica común de ingeniería, el cross-pol no es cero cuando el co-pol es diferente de la polarización pretendida o nominal del campo irradiado por la antena. En el caso de la ESD, observamos que el campo eléctrico siempre está\(\hat{\bf \theta}\) polarizado, y por lo tanto consideramos que es la polarización nominal. Dado que la polarización real de la ESD en el ejemplo es precisamente la misma que la polarización nominal de la ESD, el polo cruzado de la ESD ideal es cero. Si, por otro lado,\(\hat{\bf \theta}\) definimos arbitrariamente que es la polarización nominal y aplicamos esta definición a una antena diferente que no produce un campo eléctrico uniformemente\(\hat{\bf \theta}\) polarizado, entonces observamos cross-pol distinto de cero. El cross-pol se usa de manera similar para cuantificar los efectos debidos a errores en la posición u orientación, o debido a la modificación indeseada del campo debido a materiales (por ejemplo, estructuras de alimentación o montaje) cerca de la antena de transmisión. Resumiendo:
Co-pol se define comúnmente como la polarización pretendida o nominal para una aplicación particular, que no es necesariamente la polarización real radiada por la antena bajo consideración. Cross-pol mide la polarización en el plano ortogonal; es decir, la desviación de la supuesta copol.
Regresando a la ESD: Dado que\(\widetilde{\bf E}({\bf r})\) depende solo de\(\theta\) y no\(\phi\), el patrón de copol es el mismo en cualquier plano que contenga el\(z\) eje. Nos referimos a cualquier avión como el plano E. En general:
El plano E es cualquier plano en el que se\(\widetilde{\bf E}\) encuentra el vector nominal o previsto.
Dado que el ESD está\(\hat{\bf \theta}\) polarizado, el patrón del plano E del ESD es simplemente:
\[\left|\widetilde{\bf E}({\bf r})\right| \approx \eta \frac{I_0\cdot\beta L}{8\pi} ~\left(\sin\theta\right) ~\frac{1}{r} \label{m0205_eEESD} \]
Este patrón se muestra en la Figura\(\PageIndex{1}\).
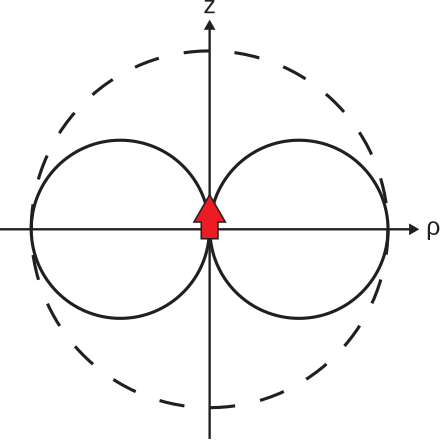
La ecuación\ ref {M0205_EEESD} se conoce como un patrón no normalizado. El patrón normalizado asociado se aborda más adelante en esta sección.
Del mismo modo, definimos el plano H de la siguiente manera:
El plano H es cualquier plano en el que\(\widetilde{\bf H}\) se encuentra el vector nominal o previsto, y así es perpendicular tanto al plano E como a la dirección de propagación.
En el caso de la ESD, el único plano H es el\(z=0\) plano. El patrón del plano H se muestra en la Figura\(\PageIndex{2}\).
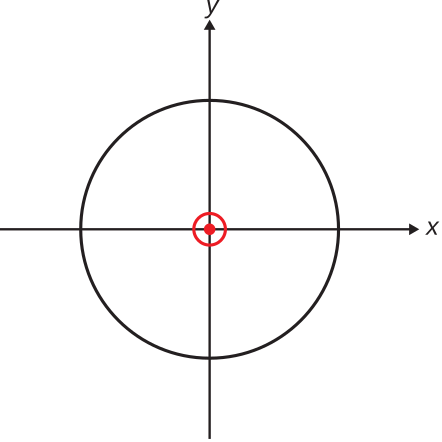
A menudo es útil normalizar el patrón, lo que significa que escalamos el patrón para que su magnitud máxima corresponda a un valor conveniente. Hay dos escalamientos comunes. Una escala común establece el valor máximo del patrón igual a 1 y, por lo tanto, es independiente de la magnitud y distancia de la fuente. Esto se conoce como el patrón normalizado. El patrón de co-pol normalizado se puede definir de la siguiente manera:
\[F(\theta,\phi) \triangleq \frac{\left|\hat{\bf e}\cdot\widetilde{\bf E}({\bf r})\right|}{\left|\hat{\bf e}\cdot\widetilde{\bf E}({\bf r})\right|_{max}} \label{m0205_eNormPat} \]
donde\(\hat{\bf e}\) es la dirección de referencia de copol, y el denominador es el valor máximo del campo eléctrico a distancia\(r\).
Un patrón normalizado se escala a una magnitud máxima de 1, usando la definición expresada en la Ecuación\ ref {M0205_enormPAT}.
Obsérvese que el valor de\(r\) es irrelevante, ya que el numerador y el denominador ambos escalan con\(r\) de la misma manera. Así, el patrón normalizado, al igual que la directividad, no cambia con la distancia desde la antena.
Para la ESD,\(\hat{\bf e}=\hat{\bf \theta}\), por lo que el patrón normalizado de copol es:
\[F(\theta,\phi) = \frac{\left|\hat{\bf \theta}\cdot\widetilde{\bf E}({\bf r})\right|}{\left|\hat{\bf \theta}\cdot\widetilde{\bf E}({\bf r})\right|_{max}} ~~~ \mbox{(ESD)} \nonumber \]
que rinde simplemente
\[F(\theta,\phi) \approx \sin\theta ~~~ \mbox{(ESD)} \nonumber \]
Así, el patrón de copol normalizado del plano E de la ESD es Figura\(\PageIndex{1}\) donde el radio del círculo de valor máximo es igual a 1, que es 0 dB. De manera similar, el patrón de copol normalizado en el plano H de la ESD es Figura\(\PageIndex{2}\) donde el radio del círculo es igual a 1 (0 dB).
El otro escalado común para patrones establece el valor máximo igual a directividad máxima. La directividad es proporcional a la densidad de potencia, que es proporcional a\(\left|\widetilde{\bf E}({\bf r})\right|^2\). Por lo tanto, este patrón de “directividad normalizada” se puede expresar como:
\[D_{max}\left|F(\theta,\phi)\right|^2 \nonumber \]
donde\(D_{max}\) está la directividad en cualquier dirección que sea máxima. Para la EDS considerada previamente,\(D_{max}=1.5\) (Sección 10.7). Por lo tanto, el patrón de copol de la ESD usando este escalado particular es
\[1.5 \sin^2\theta ~~~ \mbox{(ESD)} \nonumber \]
Así, el patrón de copol del plano E de la ESD usando esta escala es similar a la Figura\(\PageIndex{1}\), excepto que es cuadrado en magnitud y el radio del círculo de valor máximo es igual a 1.5, que es 1.76 dB. El patrón de copol del plano H de la ESD, usando esta escala, es Figura\(\PageIndex{2}\) donde el radio del círculo es igual a 1.5 (1.76 dB).
Patrón de lóbulos
Casi todas las antenas de uso común exhiben una directividad mayor que la de la ESD. Los patrones de estas antenas posteriormente exhiben una estructura más compleja. La figura\(\PageIndex{3}\) muestra un ejemplo.
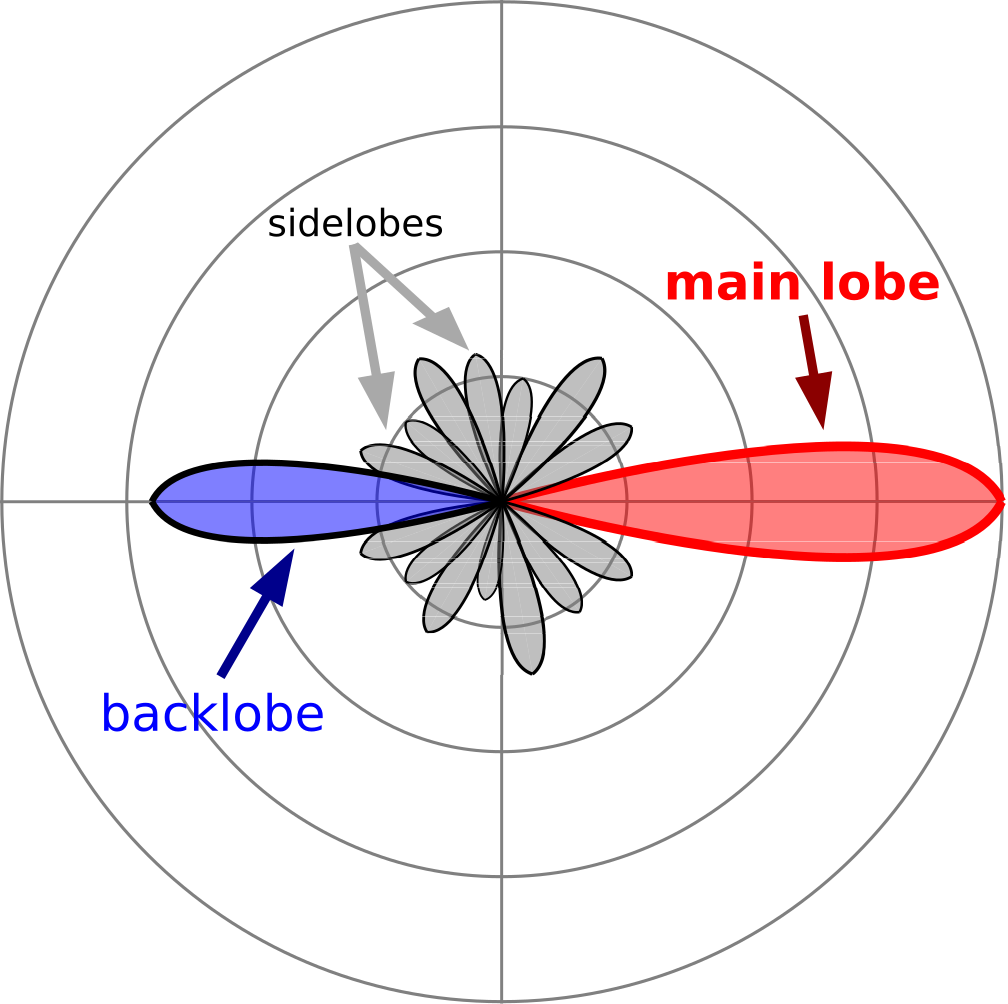
La región alrededor de la dirección de la directividad máxima se conoce como el lóbulo principal. El lóbulo principal está delimitado a cada lado por un nulo, donde la magnitud alcanza un mínimo local, quizás cero. Muchas antenas también exhiben un lóbulo en la dirección opuesta, conocido como lóbulo posterior. (Muchas otras antenas exhiben un nulo en esta dirección.) Los lóbulos entre el lóbulo principal y el lóbulo posterior se denominan lóbulos laterales. Otras métricas de patrón de uso común incluyen el primer nivel de lóbulo lateral, que es la relación de la magnitud máxima del lóbulo lateral más cercano al lóbulo principal al del lóbulo principal; y la relación delantero-atrás, que es la relación de la magnitud máxima del lóbulo posterior a la del lóbulo principal .
Cuando el lóbulo principal es estrecho, es común caracterizar el patrón en términos de ancho de haz de media potencia (HPBW). Esto se muestra en la Figura\(\PageIndex{4}\).
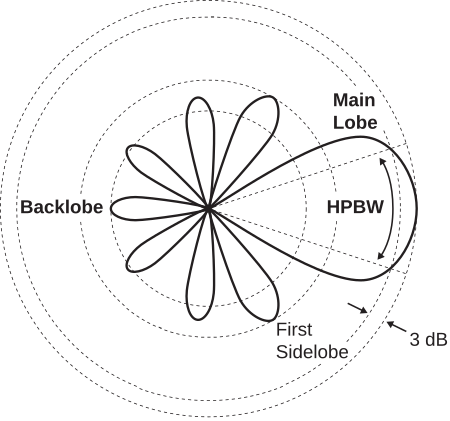
HPBW es el ancho del lóbulo principal medido entre dos puntos en los que la directividad es la mitad de su valor máximo. Como métrica de patrón, HPBW depende del plano en el que se mide. En particular, HPBW puede ser diferente en los planos E y H. Por ejemplo, se encuentra que la HPBW del plano E de la ESD es\(90^{\circ}\), mientras que la HPBW del plano H no está definida ya que el patrón es constante en el plano H.
Antenas omnidireccionales e isotrópicas
El ESD es un ejemplo de una antena omnidireccional. Una antena omnidireccional es una antena cuya magnitud de patrón es nominalmente constante en un plano que contiene la directividad máxima. Para el ESD, este plano es el plano H, por lo que se dice que el ESD es omnidireccional en el plano H. El término “omnidireccional” no indica patrón constante en todas las direcciones. (De hecho, tenga en cuenta que la ESD exhibe valores nulos de patrón en dos direcciones).
Una antena omnidireccional, como la ESD, exhibe directividad constante y nominalmente máxima en un plano.
Se dice que una antena cuyo patrón es uniforme en todas las direcciones es isotrópica. Ninguna antena físicamente realizable es isotrópica; de hecho, la ESD es lo más cercana que se puede conseguir. Sin embargo, el concepto de “antena isotrópica” es útil como estándar contra el cual se pueden cuantificar otras antenas. Dado que el patrón de una antena isotrópica es constante con la dirección, la densidad de potencia radiada por dicha antena en cualquier dirección es igual a la densidad de potencia promediada en todas las direcciones. Así, la directividad de una antena isotrópica es exactamente 1. La directividad de cualquier otra antena puede expresarse en unidades de “dBi”, que es simplemente dB en relación con la de una antena isotrópica. Por ejemplo, la directividad máxima de la ESD es 1.5, que es\(10\log_{10}\left(1.5/1\right)\)\(=\) 1.76 dBi. Resumiendo:
Una antena isotrópica exhibe directividad constante en todas las direcciones. Tal antena no es físicamente realizable, pero sin embargo es útil como línea de base para describir otras antenas.
Lectura adicional:
- “Patrón de radiación” en Wikipedia.