Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

Inicio
Ingeniería
Libro: Electromagnetica II (Ellingson)
10: Antenas
10.9: Modelo de circuito equivalente para recepción

10.9: Modelo de circuito equivalente para recepción

Última actualización

30 oct 2022
Guardar como PDF
- 10.8: Patrón de radiación
- 10.10: Reciprocidad

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

En esta sección, comenzamos a abordar las antenas como dispositivos que convierten las ondas electromagnéticas incidentes en potenciales y corrientes en un circuito. Es conveniente representar este proceso en forma de un circuito equivalente a Thévenin. El circuito particular abordado en esta sección se muestra en la Figura $\PageIndex{1}$ .

Figura $\PageIndex{1}$ : Circuito equivalente a Thévenin para una antena en presencia de una onda electromagnética incidente. (CC BY-SA 4.0 (modificado); S. Lally)

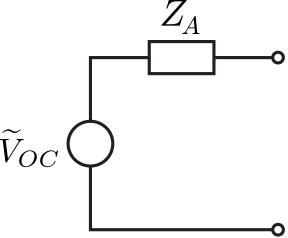
El circuito consta de una fuente de voltaje $\widetilde{V}_{OC}$ y una impedancia en serie $Z_A$ . El potencial fuente $\widetilde{V}_{OC}$ es el potencial en los terminales de la antena cuando no hay terminación; es decir, cuando la antena está en circuito abierto. La impedancia en serie $Z_A$ es la impedancia de salida del circuito, y así determina la magnitud y fase de la corriente en los terminales una vez que se conecta una carga. Dada $\widetilde{V}_{OC}$ y la corriente a través del circuito equivalente, es posible determinar la potencia entregada a la carga. Así, este modelo es bastante útil, pero sólo si somos capaces de determinar $\widetilde{V}_{OC}$ y $Z_A$ . Esta sección proporciona una derivación informal de estas cantidades que es suficiente para abordar productivamente los temas importantes posteriores de la adaptación efectiva de apertura e impedancia de las antenas receptoras. ¹

Longitud efectiva del vector

Sin que se requiera derivación, podemos deducir lo siguiente sobre $\widetilde{V}_{OC}$ :

$\widetilde{V}_{OC}$ debe depender de la intensidad del campo eléctrico incidente $\widetilde{\bf E}^i$ . Presumiblemente la relación es lineal, por lo que $\widetilde{V}_{OC}$ es proporcional a la magnitud de $\widetilde{\bf E}^i$ .
Dado que $\widetilde{\bf E}^i$ es un vector mientras que $\widetilde{V}_{OC}$ es un escalar, debe haber algún vector ${\bf l}_e$ para el cual
$\widetilde{V}_{OC}=\widetilde{\bf E}^i\cdot{\bf l}_e \label{m0206_Voc}$
Ya que $\widetilde{\bf E}^i$ tiene unidades base SI de V/m y $\widetilde{V}_{OC}$ tiene unidades base SI de V, ${\bf l}_e$ debe tener unidades base SI de m; es decir, longitud.
Esperamos que eso $\widetilde{V}_{OC}$ aumente a medida que aumenta el tamaño de la antena, por lo que la magnitud de ${\bf l}_e$ probable aumenta con el tamaño de la antena.
La dirección de ${\bf l}_e$ debe estar relacionada con la orientación del campo eléctrico incidente relativo al de la antena, ya que esto es claramente importante pero aún no lo hemos contabilizado ya.

Puede parecer en este punto que ${\bf l}_e$ está inequívocamente determinado, y solo necesitamos derivar su valor. Sin embargo, este no es el caso. De hecho, hay múltiples definiciones únicas de ${\bf l}_e$ que reducirán el vector $\widetilde{\bf E}^i$ al escalar observado a $\widetilde{V}_{OC}$ través de la ecuación\ ref {m0206_VOC}. En esta sección, emplearemos la definición más utilizada, en la que ${\bf l}_e$ se conoce como longitud efectiva del vector. Siguiendo esta definición, la parte escalar $l_e$ de ${\bf l}_e=\hat{\bf l} l_e$ se conoce comúnmente como cualquiera de los siguientes: longitud efectiva (el término utilizado en este libro), altura efectiva o factor de antena.

En esta sección, nos limitaremos a definir la longitud efectiva del vector, y diferir una derivación formal a la Sección 10.11. En esta definición, establecemos arbitrariamente $\hat{\bf l}$ , el vector unitario de valor real que indica la dirección de ${\bf l}_e$ , igual a la dirección en la que el campo eléctrico transmitido desde esta antena estaría polarizado en el campo lejano. Por ejemplo, considere un $\hat{\bf z}$ dipolo eléctricamente corto (ESD) orientado, localizado en el origen. El campo eléctrico transmitido desde esta antena tendría solo un $\hat{\bf \theta}$ componente, y ningún $\hat{\bf \phi}$ componente (y ciertamente ningún $\hat{\bf r}$ componente). Así, $\hat{\bf l}=\hat{\bf \theta}$ en este caso.

Aplicando esta definición, se $\widetilde{\bf E}^i \cdot \hat{\bf l}$ produce el componente escalar de $\widetilde{\bf E}^i$ que se copolariza con el campo eléctrico irradiado por la antena al transmitir. Ahora $l_e$ se define de manera única para ser el factor que convierte este componente en $\widetilde{V}_{OC}$ . Resumiendo:

La longitud efectiva del vector ${\bf l}_e = \hat{\bf l} l_e$ se define de la siguiente manera: $\hat{\bf l}$ es el vector unitario de valor real correspondiente a la polarización del campo eléctrico que se transmitiría desde la antena en el campo lejano. Posteriormente, la longitud efectiva $l_e$ es

$l_e \triangleq \frac{\widetilde{V}_{OC}}{\widetilde{\bf E}^i \cdot \hat{\bf l}} \nonumber$

donde $\widetilde{V}_{OC}$ es el potencial de circuito abierto inducido en los terminales de antena en respuesta a la intensidad del campo eléctrico incidente $\widetilde{\bf E}^i$ .

Si bien esta definición arroja un valor inequívoco para $l_e$ , aún no está claro cuál es ese valor. Para la mayoría de las antenas, la longitud efectiva es bastante difícil de determinar directamente, y en su lugar se debe determinar la longitud efectiva indirectamente a partir de las características de transmisión vía reciprocidad. Este enfoque es relativamente fácil (aunque todavía bastante esfuerzo) para dipolos delgados, y se presenta en la Sección 10.11.

Para dar un ejemplo de cómo funciona la longitud efectiva de inmediato, considere la ESD $\hat{\bf z}$ orientada descrita anteriormente en esta sección. Que la duración de esta ESD sea $L$ . Dejar $\widetilde{\bf E}^i$ ser una onda plana $\hat{\bf \theta}$ -polarizada que llega a la ESD. El ESD es de circuito abierto, por lo que el potencial inducido en sus terminales lo es $\widetilde{V}_{OC}$ . Se observa lo siguiente:

Cuando $\widetilde{\bf E}^i$ llega desde cualquier parte del $\theta=\pi/2$ avión (es decir, anchas a la ESD), $\widetilde{\bf E}^i$ apunta en la $-\hat{\bf z}$ dirección, y nos encontramos con eso $l_e\approx L/2$ . No debe sorprender que $l_e$ sea proporcional a $L$ ; esta expectativa se señaló anteriormente en esta sección.
Cuando $\widetilde{\bf E}^i$ llega desde las direcciones $\theta=0$ o $\theta=\pi$ —es decir, a lo largo del eje de la ESD— $\widetilde{\bf E}^i$ es perpendicular al eje de la ESD. En este caso, encontramos que $l_e$ es igual a cero.

Tomados en conjunto, estos hallazgos sugieren que $l_e$ debe contener un factor de $\sin\theta$ . Concluimos que la longitud efectiva del vector para una ESD $\hat{\bf z}$ dirigida de longitud $L$ es

${\bf l}_e \approx \hat{\bf \theta}\frac{L}{2}\sin\theta ~~~~~ \mbox{(ESD)} \label{m0206_eVEL-ESD}$

Ejemplo $\PageIndex{1}$ : Potential induced in an ESD

Un dipolo recto delgado de 10 cm de longitud se ubica en el origen y alineado con el $z$ eje. Una onda plana es incidente en el dipolo desde la dirección $(\theta=\pi/4,\phi=\pi/2)$ . La frecuencia de la onda es de 30 MHz. La magnitud del campo eléctrico incidente es $10~\mu$ V/m (rms). ¿Cuál es la magnitud del potencial de circuito abierto inducido cuando el campo eléctrico está $\hat{\bf \theta}$ polarizado (a) y (b) $\hat{\bf \phi}$ polarizado?

Solución

La longitud de onda en este ejemplo es $c/f\cong 10$ m, por lo que este dipolo es eléctricamente corto. Usando la ecuación\ ref {M0206_Evel-ESD}:

$\begin{aligned} {\bf l}_e & \approx \hat{\bf \theta}\frac{10~\mbox{cm}}{2}\sin\frac{\pi}{4} \nonumber \\ & \approx \hat{\bf \theta}\left(3.54~\mbox{cm}\right) \nonumber\end{aligned} \nonumber$

Así, la longitud efectiva $l_e=3.54$ cm. Cuando el campo eléctrico está $\hat{\bf \theta}$ polarizado, la magnitud del voltaje de circuito abierto inducido es

$\begin{aligned} \left|\widetilde{V}_{OC}\right| &=\left| \widetilde{\bf E}^i \cdot {\bf l}_e \right| \nonumber \\ &\approx \left(10~\mu\mbox{V/m}\right)\hat{\bf \theta} \cdot \hat{\bf \theta}\left(3.54~\mbox{cm}\right) \nonumber \\ &\approx \underline{354~\mbox{nV}~~\mbox{rms}}~~~ \mbox{(a)} \nonumber\end{aligned} \nonumber$

Cuando el campo eléctrico está $\hat{\bf \phi}$ polarizado:

$\begin{aligned} \left|\widetilde{V}_{OC}\right| &\approx \left(10~\mu\mbox{V/m}\right)\hat{\bf \phi} \cdot \hat{\bf \theta}\left(3.54~\mbox{cm}\right) \nonumber \\ &\approx \underline{0} ~~~ \mbox{(b)} \nonumber\end{aligned} \nonumber$

Esto se debe a que la polarización del campo eléctrico incidente es ortogonal a la de la ESD. De hecho, la respuesta a la parte (b) es cero para cualquier ángulo de incidencia $(\theta,\phi)$ .

Impedancia de salida

La impedancia de salida $Z_A$ es algo más difícil de determinar sin una derivación formal, lo cual se presenta en la Sección 10.12. Para los efectos de esta sección, basta con saltar directamente al resultado:

La impedancia $Z_A$ de salida del circuito equivalente para una antena en el caso de recepción es igual a la impedancia de entrada de la misma antena en el caso de transmisión.

Este hecho notable es consecuencia de la propiedad de reciprocidad de los sistemas de antenas, y simplifica enormemente el análisis de las antenas receptoras.

Ahora una demostración de cómo se puede utilizar el circuito equivalente de antena para determinar la potencia entregada por una antena a un circuito eléctrico conectado:

Ejemplo $\PageIndex{2}$ : Power captured by an ESD

Continuando con la parte (a) del Ejemplo $\PageIndex{1}$ : Si esta antena se termina en una carga conjugada, entonces ¿cuál es la potencia entregada a esa carga? Supongamos que la antena no tiene pérdidas.

Solución

Primero, determinamos la impedancia $Z_A$ del circuito equivalente de la antena. Esto es igual a la impedancia de entrada de la antena en transmisión. Dejar $R_A$ y $X_A$ ser las partes reales e imaginarias de esta impedancia; es decir, $Z_A=R_A+jX_A$ . Además, $R_A$ es la suma de la resistencia a la radiación $R_{rad}$ y la resistencia a la pérdida. La resistencia a la pérdida es cero debido a que la antena no tiene pérdidas. Dado que se trata de un ESD:

$R_{rad} \approx 20\pi^2 \left(\frac{L}{\lambda}\right)^2 \nonumber$

Por lo tanto, $R_A = R_{rad}\approx 4.93$ m $\Omega$ . No necesitamos calcular $X_A$ , como se hará evidente en el siguiente paso.

Una carga conjugada tiene impedancia $Z_A^*$ , por lo que el potencial $\widetilde{V}_L$ a través de la carga es

$\widetilde{V}_L = \widetilde{V}_{OC}\frac{Z_A^*}{Z_A+Z_A^*} = \widetilde{V}_{OC}\frac{Z_A^*}{2R_A} \nonumber$

La corriente $\widetilde{I}_L$ a través de la carga es

$\widetilde{I}_L = \frac{\widetilde{V}_{OC}}{Z_A+Z_A^*} = \frac{\widetilde{V}_{OC}}{2R_A} \nonumber$

Tomando $\widetilde{V}_{OC}$ como una cantidad RMS, la potencia $P_L$ entregada a la carga es

$P_L = \mbox{Re}\left\{V_L I_L^*\right\} = \frac{\left|\widetilde{V}_{OC}\right|^2}{4R_A} \nonumber$

En la parte (a) del Ejemplo $\PageIndex{1}$ , $\left|\widetilde{V}_{OC}\right|$ se encuentra que es $\approx 354$ nV rms, así $P_L \approx \underline{6.33 \text{ pW}}$ .

Las derivaciones formales de estas cantidades se proporcionan en secciones posteriores. El punto de partida es la sección sobre reciprocidad. ↩

Longitud efectiva del vector

Ejemplo\PageIndex{1}\PageIndex{1}: Potential induced in an ESD

Solución

Impedancia de salida

Ejemplo\PageIndex{2}\PageIndex{2}: Power captured by an ESD

Solución

Support Center

How can we help?

Ejemplo $\PageIndex{1}$ : Potential induced in an ESD

Ejemplo $\PageIndex{2}$ : Power captured by an ESD