5.4: La fórmula cuadrática

Considerar la función cuadrática general $$f(x)=a x^{2}+b x+c$$

En la sección anterior, aprendimos que podemos encontrar los ceros de esta función resolviendo la ecuación $$f(x)=0$$

Si sustituimos$f(x) = ax^2 + bx + c$, entonces la ecuación resultante $$a x^{2}+b x+c=0$$

se llama una ecuación cuadrática. En la sección anterior, resolvimos ecuaciones de este tipo factorizando y utilizando la propiedad cero del producto.

Sin embargo, no siempre es posible factorizar el trinomio en el lado izquierdo de la ecuación cuadrática (1) como producto de factores con coeficientes enteros. Por ejemplo, considere la ecuación cuadrática $$2 x^{2}+7 x-3=0$$

Comparando$2x^2 + 7x − 3$ con$ax^2 + bx + c$, vamos a enumerar todos los pares enteros cuyo producto es ac = (2) (−3) = −6.

Ni uno solo de estos pares enteros se suma a b = 7. Por lo tanto, el trinomio cuadrático$2x^2 + 7x − 3$ no factoriza sobre los enteros. En consecuencia, necesitaremos otro método para resolver la ecuación cuadrática (2).

El propósito de esta sección es desarrollar una fórmula que proporcione consistentemente soluciones de la ecuación cuadrática general (1). Sin embargo, antes de que podamos desarrollar la “Fórmula Cuadrática”, necesitamos sentar algunas bases que involucren las raíces cuadradas de los números.

Raíces Cuadradas

Comenzamos nuestra discusión sobre las raíces cuadradas investigando las soluciones de la ecuación$x^2 = a$. Considera la ecuación bastante simple

$$x^{2}=25$$

Porque$(−5)^2 = 25$ y$(5)^2 = 25$, la ecuación (3) tiene dos soluciones, x = −5 o x = 5. Usualmente denotamos estas soluciones simultáneamente, usando un signo “más o menos”:

$$x=\pm 5$$

Estas soluciones se denominan raíces cuadradas de 25. Debido a que hay dos soluciones, necesitamos una notación diferente para cada una. Denotaremos la raíz cuadrada positiva de 25 con la notación$\sqrt{25}$ y la raíz cuadrada negativa de 25 con la notación$-\sqrt{25}$. Por lo tanto,

$$\sqrt{25}=5 \qquad \text { and } \qquad-\sqrt{25}=-5$$

En una línea similar, la ecuación$x^{2}=36$ tiene dos soluciones$x=\pm \sqrt{36}$, o alternativamente,$x=\pm 6$. La notación$\sqrt{36}$ llama a la raíz cuadrada positiva, mientras que la notación$-\sqrt{36}$ llama a la raíz cuadrada negativa. Es decir, $$\sqrt{36}=6 \qquad \text { and } \qquad-\sqrt{36}=-6$$

No es necesario que el lado derecho de la ecuación$x^2 = a$ sea un “cuadrado perfecto”. Por ejemplo, la ecuación

$$x^{2}=7 \quad \text { has solutions } \quad x=\pm \sqrt{7}$$

No hay raíz cuadrada racional de 7. Es decir, no hay manera de expresar la raíz cuadrada de 7 en la forma p/q, donde p y q son enteros. Por lo tanto,$\sqrt{7}$ es un ejemplo de un número irracional. Sin embargo,$\sqrt{7}$ es un número real perfectamente válido y nos sentimos perfectamente cómodos dejando nuestra respuesta en la forma que se muestra en la ecuación (4).

Sin embargo, si se necesita una aproximación para la raíz cuadrada de 7, podemos razonar que debido a que 7 se encuentra entre 4 y 9, la raíz cuadrada de 7 estará entre 2 y 3. Debido a que 7 está más cerca de 9 que 4, una aproximación razonable podría ser

$$\sqrt{7} \approx 2.6$$

Una calculadora puede proporcionar una aproximación aún mejor. Por ejemplo, nuestros informes TI83

$$\sqrt{7} \approx 2.645751311$$

Hay dos casos degenerados que involucran la ecuación$x^2 = a$ que exigen nuestra atención.

1. La ecuación$x^{2}=0$ tiene una sola solución, a saber x = 0. Por lo tanto,$\sqrt{0} = 0$.
2. La ecuación no$x^{2}=-4$ tiene soluciones reales.4 No es posible cuadrar un número real y obtener −4. Ante esta situación, simplemente vamos a afirmar que “la ecuación no$x^{2}=-4$ tiene soluciones reales (no hay soluciones que sean números reales)”.

Ejemplo$\PageIndex{1}$

Encuentra todas las soluciones reales de las ecuaciones$x^2 = 30, x^2 = 0, and x^2 = −14$.

Solución

Las soluciones siguen.

• La ecuación$x^2 = 30$ tiene dos soluciones reales, a saber$x=\pm \sqrt{30}$.
• La ecuación$x^2 = 0$ tiene una solución real, a saber x = 0.
• La ecuación no$x^2 = -14$ tiene soluciones reales.

Probemos ejemplos adicionales.

Ejemplo$\PageIndex{2}$

Encuentra todas las soluciones reales de la ecuación$(x + 2)^2 = 43$.

Solución

Hay dos posibilidades para x + 2, a saber $$x+2=\pm \sqrt{43}$$

Para resolver para x, resta 2 de ambos lados de esta última ecuación. $$x=-2 \pm \sqrt{43}$$

Si bien esta última respuesta suele ser la forma preferible de la respuesta, hay algunas ocasiones en las que se necesita una aproximación. Entonces, nuestro TI83 da las siguientes aproximaciones.

$$-2-\sqrt{43} \approx-8.557438524 \qquad \text { and } \qquad-2+\sqrt{43} \approx 4.557438524$$

Ejemplo$\PageIndex{3}$

Encuentra todas las soluciones reales de la ecuación$(x − 4)^2 = −15$.

Solución

Si x es un número real, entonces también lo es x − 4. No es posible cuadrar el número real x − 4 y obtener −15. Por lo tanto, este problema no tiene soluciones reales.

Desarrollo de la Fórmula Cuadrática

Ahora tenemos todas las bases para buscar una solución de la ecuación cuadrática general

$$a x^{2}+b x+c=0$$

Vamos a usar una forma de “completar el cuadrado” para resolver esta ecuación para x Comencemos restando c de ambos lados de la ecuación.

$$a x^{2}+b x=-c$$

A continuación, divida ambos lados de la ecuación por a. $$x^{2}+\frac{b}{a} x=-\frac{c}{a}$$

Toma la mitad del coeficiente de x, como en (1/2) (b/a) = b/ (2a). Cuadrado este resultado para obtener$b^{2} /\left(4 a^{2}\right)$. Agrega esta cantidad a ambos lados de la ecuación.

$$x^{2}+\frac{b}{a} x+\frac{b^{2}}{4 a^{2}}=-\frac{c}{a}+\frac{b^{2}}{4 a^{2}}$$

A la izquierda facetamos el trinomio cuadrado perfecto. A la derecha obtenemos un denominador común y sumamos las fracciones equivalentes resultantes.

$$\begin{array}{l}{\left(x+\frac{b}{2 a}\right)^{2}=-\frac{4 a c}{4 a^{2}}+\frac{b^{2}}{4 a^{2}}} \\ {\left(x+\frac{b}{2 a}\right)^{2}=\frac{b^{2}-4 a c}{4 a^{2}}}\end{array}$$

Siempre que el lado derecho de esta última ecuación sea positivo, tenemos dos soluciones reales.

$$x+\frac{b}{2 a}=\pm \sqrt{\frac{b^{2}-4 a c}{4 a^{2}}}$$

A la derecha, tomamos la raíz cuadrada de la parte superior y la parte inferior de la fracción.

$$x+\frac{b}{2 a}=\pm \frac{\sqrt{b^{2}-4 a c}}{2 a}$$

Para completar la solución, solo necesitamos restar b/ (2a) de ambos lados de la ecuación.

$$x=-\frac{b}{2 a} \pm \frac{\sqrt{b^{2}-4 a c}}{2 a}$$

Aunque esta última respuesta es una solución perfectamente buena, habitualmente reescribimos la solución con un único denominador común.

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$

Este último resultado da la solución a la ecuación cuadrática general (8). La solución (9) se llama la fórmula cuadrática.

La fórmula cuadrática

Las soluciones a la ecuación cuadrática $$a x^{2}+b x+c=0$$ vienen dadas por la fórmula cuadrática $$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$

Si bien el desarrollo de la fórmula cuadrática puede resultar intimidante, en la práctica su aplicación es bastante sencilla. Veamos algunos ejemplos.

Ejemplo$\PageIndex{4}$

Usa la fórmula cuadrática para resolver la ecuación $$x^{2}=27-6 x$$

Solución

El primer paso es colocar la ecuación en la forma$ax^2 + bx + c = 0$ moviendo cada término a un lado de la ecuación,7 arreglando los términos en potencias descendentes de x.

$$x^{2}+6 x-27=0$$

A continuación, compare$x^2 + 6x − 27 = 0$ con la forma general de la ecuación cuadrática$ax^2 + bx + c = 0$ y observe que a = 1, b = 6 y c = −27. Copia la fórmula cuadrática.

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$

Sustituya a = 1, b = 6 y c = −27 y simplifique.

$$\begin{aligned} x &=\frac{-(6) \pm \sqrt{(6)^{2}-4(1)(-27)}}{2(1)} \\ x &=\frac{-6 \pm \sqrt{36+108}}{2} \\ x &=\frac{-6 \pm \sqrt{144}}{2} \end{aligned}$$

En este caso, 144 es un cuadrado perfecto. Es decir$\sqrt{144} = 12$, para que podamos seguir simplificando $$x=\frac{-6 \pm 12}{2}$$

Es importante señalar que hay dos respuestas reales, a saber

$$x=\frac{-6-12}{2} \quad \text { or } \qquad x=\frac{-6+12}{2}$$

Simplificando, $$x=-9 \qquad \text { or } \qquad x=3$$

Es interesante señalar que este problema podría haberse resuelto factorizando. En efecto,

$$\begin{aligned} x^{2}+6 x-27 &=0 \\(x-3)(x+9) &=0 \end{aligned}$$

por lo que la propiedad cero del producto requiere que ya sea x − 3 = 0 o x + 9 = 0, lo que lleva a x = 3 o x = −9, respuestas idénticas a las encontradas por la fórmula cuadrática.

Pronto tendremos más que decir sobre el “discriminante”, pero no es casualidad que lo cuadrático$x^2 + 6x − 27$ factorizara. Aquí está el hecho relevante.

Cuando el discriminante es un cuadrado perfecto

En la fórmula cuadrática, $$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$ el número bajo el radical,$b^2 − 4ac$, se llama el discriminante. Cuando el discriminante es un cuadrado perfecto, la función cuadrática siempre factorizará.

Sin embargo, no siempre es así que podamos factorizar la cuadrática dada. Veamos otro ejemplo.

Ejemplo$\PageIndex{5}$

Dada la función cuadrática$f(x) = x^2 − 2x$, encuentra todas las soluciones reales de f (x) = 2.

Solución

Porque$f(x) = x^2 − 2x$, la ecuación f (x) = 2 se convierte

$$x^{2}-2 x=2$$

Establezca un lado de la ecuación igual a cero restando 2 de ambos lados de la ecuación.

$$x^{2}-2 x-2=0$$

Compare$x^2 − 2x − 2 = 0$ con la ecuación cuadrática general$ax^2 + bx + c = 0$ y observe que a = 1, b = −2 y c = −2. Anota la fórmula cuadrática.

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$

A continuación, sustituya a = 1, b = −2 y c = −2. Tenga en cuenta el uso cuidadoso de paréntesis.

$$x=\frac{-(-2) \pm \sqrt{(-2)^{2}-4(1)(-2)}}{2(1)}$$

Simplificar. $$\begin{array}{l}{x=\frac{2 \pm \sqrt{4+8}}{2}} \\ {x=\frac{2 \pm \sqrt{12}}{2}}\end{array}$$

En este caso, 12 no es un cuadrado perfecto, por lo que hemos simplificado tanto como es posible en este momento.10 Sin embargo, podemos aproximar estas soluciones con la ayuda de una calculadora.

$$x=\frac{2-\sqrt{12}}{2} \approx-0.7320508076 \qquad x=\frac{2+\sqrt{12}}{2} \approx 2.732050808$$

Estas aproximaciones encontraremos útiles en lo que sigue.

Las ecuaciones en Ejemplos$\PageIndex{4}$ y$\PageIndex{5}$ representan un cambio fundamental en nuestra técnica habitual para resolver ecuaciones. En el pasado, hemos tratado de “aislar” los términos que contienen x (o lo que sea desconocido que estemos resolviendo) en un lado de la ecuación, y todos los demás términos en el otro lado de la ecuación. Ahora, en Ejemplos$\PageIndex{4}$ y$\PageIndex{5}$, nos encontramos moviendo todo a un lado de la ecuación, haciendo que un lado de la ecuación sea igual a cero. Esto lleva alguna explicación.

Lineal o no lineal

Supongamos que lo desconocido que estamos resolviendo es x.

• Si la mayor potencia de x presente en la ecuación es x a la primera potencia, entonces la ecuación es lineal. Así, por ejemplo, cada una de las ecuaciones $$2 x+3=7, \quad 3-4 x=5 x+9, \quad \text { and } \qquad a x+b=c x+d$$ es lineal.
• Si hay potencias de x mayores que x a la primera potencia en la ecuación, entonces la ecuación es no lineal. Así, por ejemplo, cada una de las ecuaciones $$x^{2}-4 x=9, \qquad x^{3}=2 x+3, \quad \text { and } \quad a x^{2}+b x=c x+d$$ es no lineal.

La estrategia para resolver una ecuación se desplazará, dependiendo de si la ecuación es lineal o no lineal.

Estrategia de solución: lineal versus no lineal

Al resolver ecuaciones, primero debe preguntar si la ecuación es lineal o no lineal. Nuevamente, supongamos que lo desconocido que deseamos resolver es x.

• Si la ecuación es lineal, mueva todos los términos que contengan x a un lado de la ecuación, todos los términos restantes al otro lado de la ecuación.
• Si la ecuación es no lineal, mueva todos los términos a un lado de la ecuación, haciendo que el otro lado de la ecuación sea cero.

Así, debido a que ax + b = cx + d es lineal en x, el primer paso para resolver la ecuación sería mover todos los términos que contienen x a un lado de la ecuación, todos los demás términos al otro lado de la ecuación, como en

$$a x-c x=d-b$$

Por otro lado, la ecuación$ax^2 + bx = cx + d$ es no lineal en x, por lo que el primer paso sería mover todos los términos a un lado de la ecuación, haciendo que el otro lado de la ecuación sea igual a cero, como en $$a x^{2}+b x-c x-d=0$$

En Ejemplo$\PageIndex{5}$, la ecuación$x^2−2x = 2$ es no lineal en x, así que movimos todo al lado izquierdo de la ecuación, haciendo que el lado derecho de la ecuación sea igual a cero, como en$x^2 −2x−2 = 0$. No obstante, no importa de qué lado hagas igual a cero. Supongamos que mueve cada término al lado derecho de la ecuación, como en $$0=-x^{2}+2 x+2$$

Comparando$0 = −x^2 + 2x + 2$ con la ecuación cuadrática general$0 = ax^2 + bx + c$, tenga en cuenta que a = −1, b = 2 y c = 2. Anota la fórmula cuadrática.

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$

A continuación, sustituya a = −1, b = 2 y c = 2. Nuevamente, tenga en cuenta el uso cuidadoso de los paréntesis.

$$x=\frac{-(2) \pm \sqrt{(2)^{2}-4(-1)(2)}}{2(-1)}$$

Esto lleva a dos soluciones, $$x=\frac{-2 \pm \sqrt{4+8}}{-2}=\frac{-2 \pm \sqrt{12}}{-2}$$

En Ejemplo$\PageIndex{5}$, encontramos las siguientes soluciones y sus aproximaciones.

$$x=\frac{2-\sqrt{12}}{2} \approx-0.7320508076 \qquad x=\frac{2+\sqrt{12}}{2} \approx 2.732050808$$

Es una pregunta justa preguntarse si nuestras soluciones$x=(-2 \pm \sqrt{12}) /(-2)$ son las mismas. Una forma de averiguarlo es encontrar aproximaciones decimales de cada una en nuestra calculadora.

$$x=\frac{-2-\sqrt{12}}{-2} \approx 2.732050808 \qquad x=\frac{-2+\sqrt{12}}{-2} \approx-0.7320508076$$

El hecho de que obtengamos las mismas aproximaciones decimales debería despertar la confianza de que tenemos las mismas soluciones. Sin embargo, también podemos manipular las formas exactas de nuestras soluciones para demostrar que coinciden con las formas anteriores que se encuentran en Ejemplo$\PageIndex{5}$.

Toma las dos soluciones y multiplica tanto el numerador como el denominador por menos uno.

$$\frac{-2-\sqrt{12}}{-2}=\frac{2+\sqrt{12}}{2} \qquad \text { and } \quad \frac{-2+\sqrt{12}}{-2}=\frac{2-\sqrt{12}}{2}$$

Esto demuestra que nuestras soluciones son idénticas a las que se encuentran en Ejemplo$\PageIndex{5}$.

Podemos hacer la misma negación del numerador y denominador en forma compacta.

$$\frac{-2 \pm \sqrt{12}}{-2}=\frac{2 \mp \sqrt{12}}{2}$$

Tenga en cuenta que esto lleva a las mismas dos respuestas,$(2-\sqrt{12}) / 2$ y$(2+\sqrt{12}) / 2$.

De los dos métodos (mover todos los términos a la izquierda o todos los términos a la derecha), preferimos el enfoque de Ejemplo$\PageIndex{5}$. Al mover los términos hacia el lado izquierdo de la ecuación, como en$x^2 − 2x − 2 = 0$, el coeficiente de$x^2$ es positivo (a = 1) y evitamos el signo menos en el denominador producido por la fórmula cuadrática.

Intercepta

En Ejemplo$\PageIndex{5}$, se utilizó la fórmula cuadrática para encontrar las soluciones de$x^2 − 2x − 2 = 0$. Estas soluciones, y sus aproximaciones, se muestran en la ecuación (14). Es importante hacer la conexión que las soluciones en la ecuación (14) son los ceros de la función cuadrática$g(x) = x^2 − 2x − 2$. Los ceros también proporcionan las coordenadas x de las intercepciones x de la gráfica de g (una parábola). Para enfatizar este punto, dibujemos la gráfica de la parábola que tiene la ecuación$g(x) = x^2 − 2x − 2$.

Primero, complete el cuadrado para colocar la función cuadrática en forma de vértice. Toma la mitad del coeficiente medio y el cuadrado, como en$[(1/2)(−2)]^2 = 1$; luego suma y resta este término para que la ecuación quede equilibrada.

$$\begin{array}{l}{g(x)=x^{2}-2 x-2} \\ {g(x)=x^{2}-2 x+1-1-2}\end{array}$$

Factorizar el trinomio cuadrado perfecto, luego combinar las constantes al final. $$g(x)=(x-1)^{2}-3$$

Se trata de una parábola que se abre hacia arriba. Se desplaza hacia la derecha 1 unidad y hacia abajo 3 unidades. Esto facilita la identificación del vértice y dibujar el eje de simetría, como se muestra en la Figura$\PageIndex{1}$ (a).

Ahora será evidente por qué utilizamos nuestra calculadora para aproximar las soluciones en (14). Estas son las coordenadas x de las intercepciones x. Una intercepción x se localiza aproximadamente en (−0.73, 0), la otra aproximadamente (2.73, 0). Estas aproximaciones se utilizan para trazar la ubicación de las intercepciones como se muestra en la Figura$\PageIndex{1}$ (b). Sin embargo, los valores reales de las intercepciones son$((2-\sqrt{12}) / 2,0)$ y$((2+\sqrt{12}) / 2,0)$, y estos valores exactos deben usarse para anotar las intercepciones, como se muestra en la Figura$\PageIndex{1}$ (b).

Finalmente, para encontrar la intercepción y, dejar x = 0 in$g(x) = x^2 − 2x − 2$. Así, g (0) = −2 y la intercepción y es (0, −2). La intercepción y y su imagen especular a través del eje de simetría se trazan en la Figura$\PageIndex{1}$ (c), donde también se muestra la gráfica final de la parábola.

Figura$\PageIndex{1}$

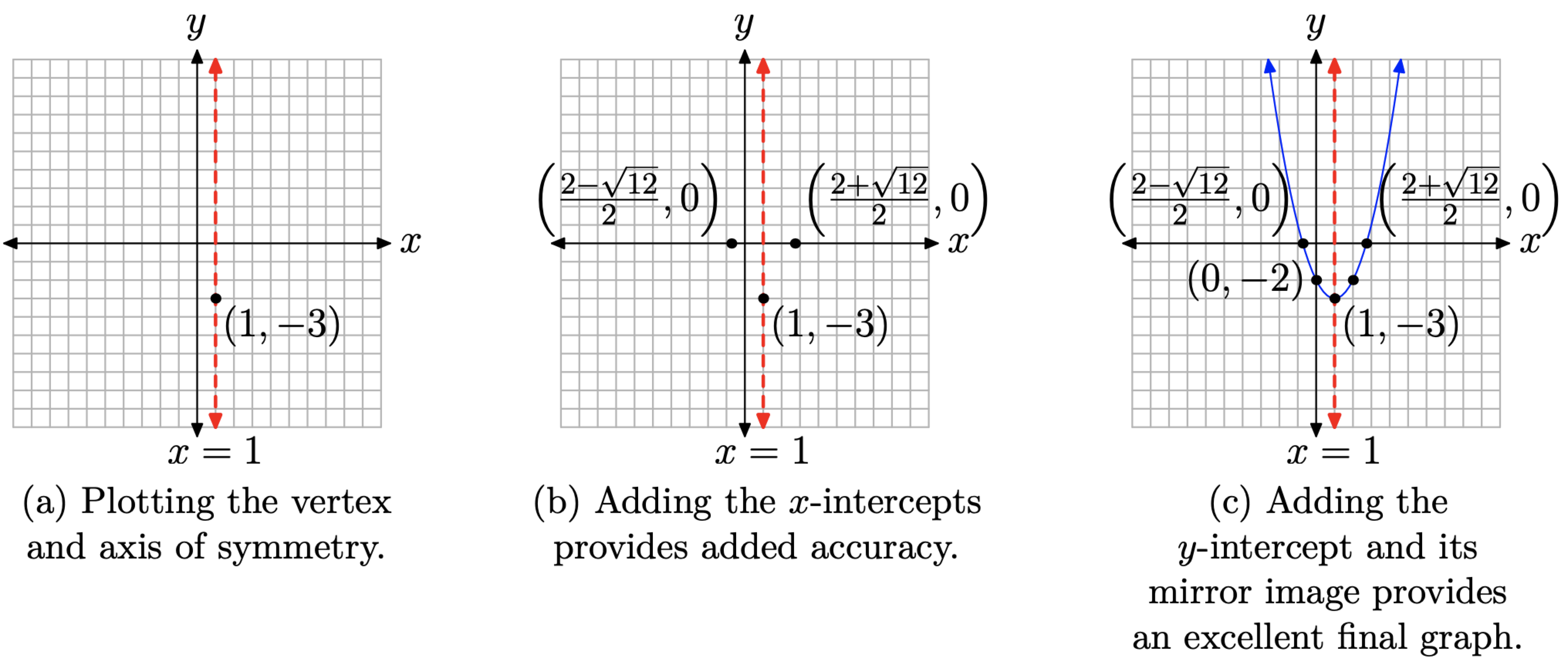
Hemos hecho un punto importante y hacemos una pausa para dar énfasis.

Ceros e Intercepciones

Siempre que uses la fórmula cuadrática para resolver la ecuación cuadrática $$a x^{2}+b x+c=0$$

las soluciones $$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$

son los ceros de la función cuadrática $$f(x)=a x^{2}+b x+c$$

Las soluciones también proporcionan las coordenadas x de las intercepciones x de la gráfica de f.

Tenemos que discutir un concepto final.

El discriminante

Consideremos nuevamente la ecuación cuadrática$ax^2 + bx + c = 0$ y las soluciones (ceros) proporcionadas por la fórmula cuadrática

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$

La expresión bajo el radical,$b^2 − 4ac$, se llama el discriminante, que denotamos con la letra D. Es decir, la fórmula para el discriminante viene dada por

$$D=b^{2}-4 a c$$

El discriminante se utiliza para determinar la naturaleza y el número de soluciones a la ecuación cuadrática$ax^2+bx+c = 0$. Esto se hace sin realmente calcular las soluciones.

Veamos tres ejemplos clave.

Ejemplo$\PageIndex{6}$

Considerar la ecuación cuadrática $$x^{2}-4 x-4=0$$ Calcular el discriminante y utilizarlo para determinar la naturaleza y el número de las soluciones.

Solución

Compare$x^2 − 4x − 4 = 0$ con$ax^2 + bx + c = 0$ y observe que a = 1, b = −4 y c = −4. El discriminante viene dado por el cálculo

$$D=b^{2}-4 a c=(-4)^{2}-4(1)(-4)=32$$

Obsérvese que el discriminante D es positivo; es decir, D > 0.

Considere la función cuadrática$f(x) = x^2 − 4x − 4$, que se puede escribir en forma de vértice

$$f(x)=(x-2)^{2}-8$$

Se trata de una parábola que se abre hacia arriba. Se desplaza hacia la derecha 2 unidades, luego hacia abajo 8 unidades. Por lo tanto, cruzará el eje x en dos ubicaciones. De ahí que uno esperaría que la fórmula cuadrática proporcionara dos soluciones reales (intercepciones x). En efecto,

$$x=\frac{-(-4) \pm \sqrt{(-4)^{2}-4(1)(-4)}}{2(1)}=\frac{4 \pm \sqrt{32}}{2}$$

Obsérvese que el discriminante, D = 32 como se calculó anteriormente, es el número bajo la raíz cuadrada. Estas soluciones tienen aproximaciones

$$x=\frac{4-\sqrt{32}}{2} \approx-0.8284271247 \qquad \text { and } \qquad x=\frac{4+\sqrt{32}}{2} \approx 4.828427125$$

que ayudan a trazar una gráfica precisa de$f(x) = (x − 2)^2 − 8$, como se muestra en la Figura$\PageIndex{2}$.

Figura$\PageIndex{2}$. Si el discriminante es positivo, hay dos intercepciones x reales.

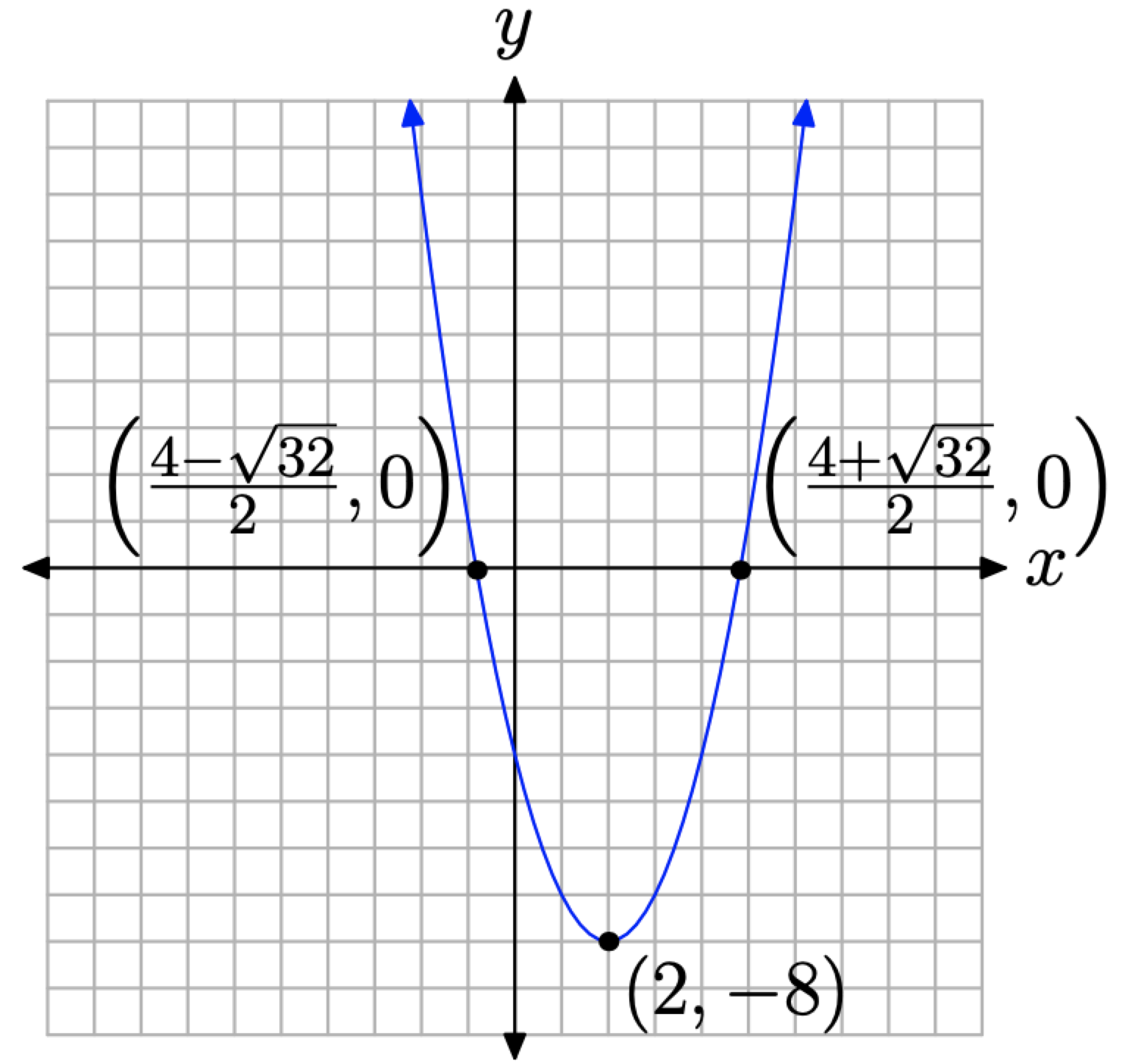
Así, si el discriminante es positivo, la parábola tendrá dos intercepciones x reales.

A continuación, veamos un ejemplo donde el discriminante es igual a cero.

Ejemplo$\PageIndex{7}$

Consideremos nuevamente la ecuación cuadrática$ax^2 + bx + c = 0$ y las soluciones (ceros) proporcionadas por la fórmula cuadrática

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$$ La expresión bajo el radical,$b^2 − 4ac$, se llama el discriminante, que denotamos con la letra D. Es decir, la fórmula para el discriminante viene dada por $$D=b^{2}-4 a c$$

El discriminante se utiliza para determinar la naturaleza y el número de soluciones a la ecuación cuadrática$ax^2+bx+c = 0$. Esto se hace sin realmente calcular las soluciones. Considerar la ecuación cuadrática $$x^{2}-4 x+4=0$$

Calcular el discriminante y utilizarlo para determinar la naturaleza y el número de las soluciones.

Solución

Compare$x^2 − 4x + 4 = 0$ con$ax^2 + bx + c = 0$ y observe que a = 1, b = −4 y c = 4. El discriminante viene dado por el cálculo

$$D=b^{2}-4 a c=(-4)^{2}-4(1)(4)=0$$

Tenga en cuenta que el discriminante es igual a cero.

Considere la función cuadrática$f(x) = x^2 − 4x + 4$, que se puede escribir en forma de vértice

$$f(x)=(x-2)^{2}$$

Se trata de una parábola que se abre hacia arriba y se desplaza 2 unidades hacia la derecha. Tenga en cuenta que no hay desplazamiento vertical, por lo que el vértice de la parábola descansará sobre el eje x, como se muestra en la Figura$\PageIndex{3}$. En este caso, nos pareció necesario trazar dos puntos a la derecha del eje de simetría, luego reflejarlos a través del eje de simetría, para obtener una gráfica precisa de la parábola.

Figura$\PageIndex{3}$. A la derecha hay una tabla de puntos satisfactorios$f(x) = (x−2)^2$. Estos puntos y sus imágenes especulares se ven como puntos sólidos superpuestos en la gráfica de$f(x) = (x − 2)^2$ la izquierda.

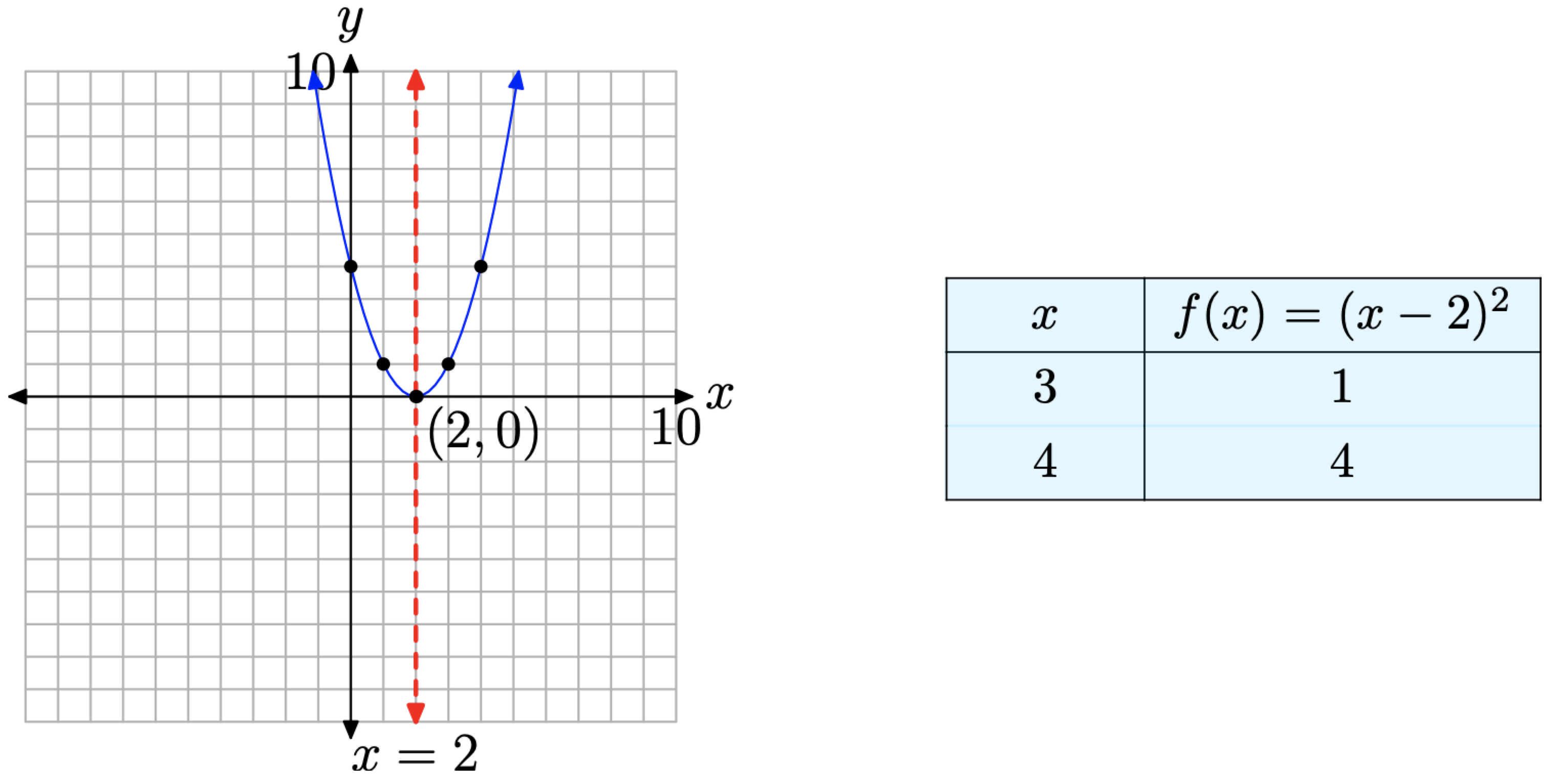
Eche un vistazo más de cerca a la ecuación (17). Si establecemos f (x) = 0 en esta ecuación, entonces obtenemos$0 = (x − 2)^2$. Esto podría escribirse 0 = (x − 2) (x − 2) y podríamos decir que las soluciones son 2 y 2 de nuevo. Sin embargo, los matemáticos prefieren decir que “2 es una solución de multiplicidad 2" o “2 es una solución doble” .11 Observe cómo la parábola es tangente al eje x en la ubicación de la “solución doble”. Es decir, la parábola baja del infinito positivo, toca (pero no cruza) el eje x en x = 2, luego vuelve a subir al infinito positivo. Por supuesto, la situación se revertiría en la parábola abierta a la baja, como en$g(x) = −(x − 2)^2$, pero la gráfica seguiría “besando” el eje x en la ubicación de la “solución doble”.

Aún así, lo clave a tener en cuenta aquí es el hecho de que el discriminante D = 0 y la parábola tiene sólo una intercepción x. Es decir, la ecuación$x^2 − 4x + 4 = 0$ tiene una única solución real.

A continuación, veamos qué pasa cuando el discriminante es negativo.

Ejemplo$\PageIndex{8}$

Considerar la ecuación cuadrática $$x^{2}-4 x+8=0$$

Calcular el discriminante y utilizarlo para determinar la naturaleza y el número de las soluciones.

Solución

Compare$x^2 − 4x + 8 = 0$ con$ax^2 + bx + c = 0$ y observe que a = 1, b = −4 y c = 8. El discriminante viene dado por el cálculo

$$D=b^{2}-4 a c=(-4)^{2}-4(1)(8)=-16$$

Obsérvese que el discriminante es negativo.

Considere la función cuadrática$f(x) = x^2 − 4x + 8$, que se puede escribir en forma de vértice

$$f(x)=(x-2)^{2}+4$$

Se trata de una parábola que se abre hacia arriba. Además, tiene que ser desplazado 2 unidades a la derecha y 4 unidades hacia arriba, por lo que no puede haber intercepciones x, como se muestra en la Figura$\PageIndex{4}$. Nuevamente, nos pareció necesario en este ejemplo trazar dos puntos a la derecha del eje de simetría, luego reflejarlos, para obtener una trama precisa de la parábola.

Figura$\PageIndex{4}$. A la derecha hay una tabla de puntos satisfactorios$f(x)=(x-2)^{2}+4$. Estos puntos y sus imágenes especulares se ven como puntos sólidos superpuestos en la gráfica de$f(x)=(x-2)^{2}+4$ la izquierda.

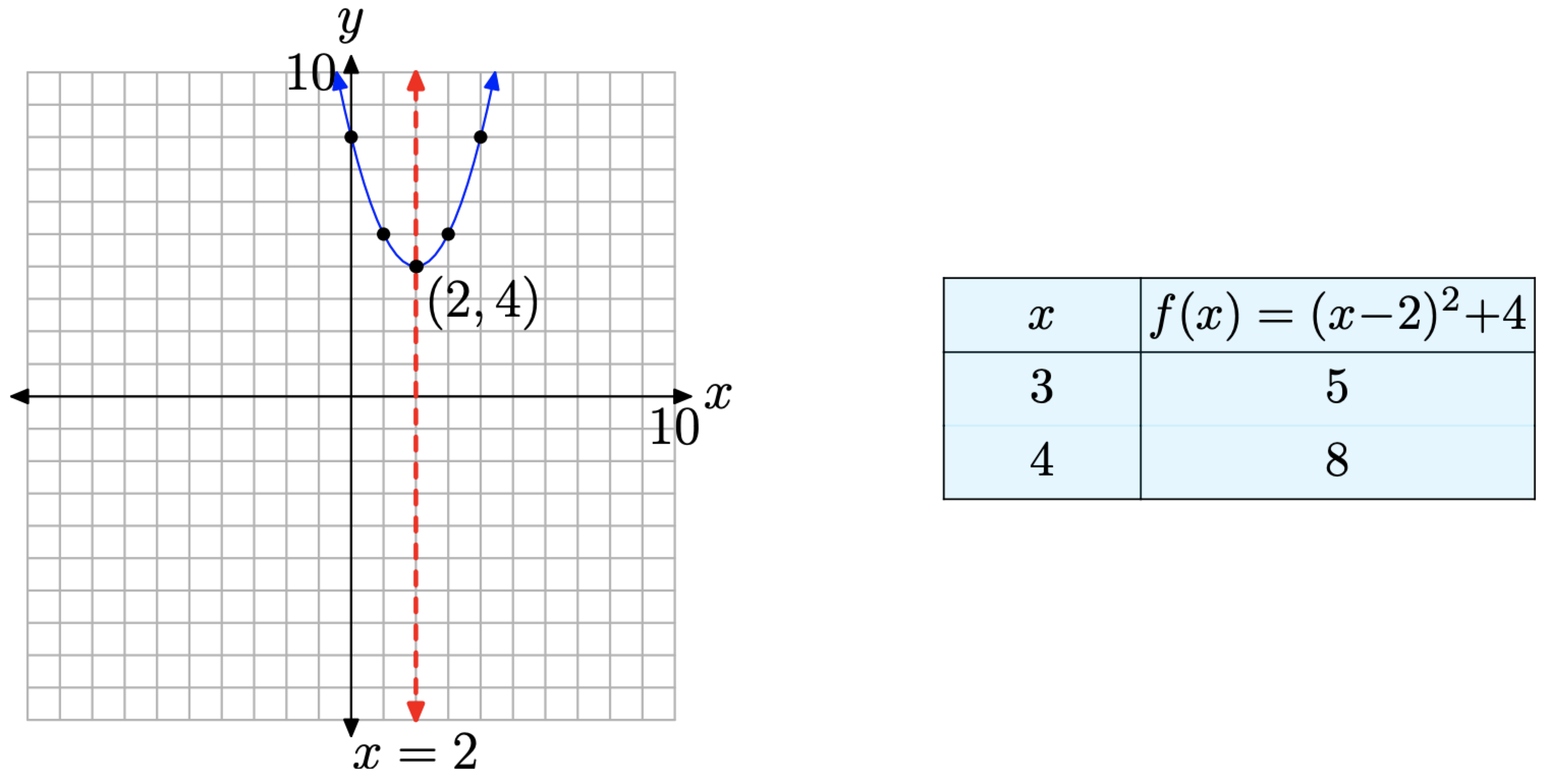
Una vez más, el punto clave en este ejemplo es el hecho de que el discriminante es negativo y no hay soluciones reales de la ecuación cuadrática (equivalentemente, no hay intercepciones x). Veamos qué pasa si realmente tratamos de encontrar las soluciones de$x^2 − 4x + 8 = 0$ usar la fórmula cuadrática. Nuevamente, a = 1, b = −4, y c = 8, por lo que $$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}=\frac{-(-4) \pm \sqrt{(-4)^{2}-4(1)(8)}}{2(1)}$$ Simplificando, $$x=\frac{4 \pm \sqrt{-16}}{2}$$

Nuevamente, recordemos que el número bajo la raíz cuadrada es el discriminante. En este caso el discriminante es −16. No es posible cuadrar un número real y obtener −16. Así, la ecuación cuadrática no$x^2 − 4x + 8 = 0$ tiene soluciones reales, como se predijo.

Resumamos los hallazgos en nuestros últimos tres ejemplos.

Resumen

Considera la ecuación cuadrática $$a x^{2}+b x+c=0$$ . El discriminante se define como $$D=b^{2}-4 a c$$ .

Hay tres posibilidades:

1. Si D > 0, entonces la ecuación cuadrática tiene dos soluciones reales.
2. Si D = 0, entonces la ecuación cuadrática tiene una solución real.
3. Si D < 0, entonces la ecuación cuadrática no tiene soluciones reales.

Este resultado clave se refleja en la gráfica de la función cuadrática.

Resumen

Considera la función cuadrática $$f(x)=a x^{2}+b x+c$$ .

La gráfica de esta función es una parábola. Existen tres posibilidades dependiendo del valor del discriminante$D = b^2 − 4ac$.

1. Si D > 0, la parábola tiene dos intercepciones x.
2. Si D = 0, la parábola tiene exactamente una intercepción x.
3. Si D < 0, la parábola no tiene intercepciones x.

Ejercicio

En los Ejercicios 1 - 8, encuentra todas las soluciones reales de la ecuación dada. Usa una calculadora para aproximar las respuestas, corregir a la centésima más cercana (dos decimales).

Ejercicio$\PageIndex{1}$

$x^2 = 36$

Contestar

$x = \pm 6$

Ejercicio$\PageIndex{2}$

$x^2 = 81$

Ejercicio$\PageIndex{3}$

$x^2 = 17$

Contestar

$x = \pm \sqrt{17} \approx \pm 4.12$

Ejercicio$\PageIndex{4}$

$x^2 = 13$

Ejercicio$\PageIndex{5}$

$x^2 = 0$

Responder

x = 0

Ejercicio$\PageIndex{6}$

$x^2 = −18$

Ejercicio$\PageIndex{7}$

$x^2 = −12$

Responder

No hay una solución real

Ejercicio$\PageIndex{8}$

$x^2 = 3$

En los Ejercicios 9 - 16, encuentra todas las soluciones reales de la ecuación dada. Usa una calculadora para aproximar tus respuestas a la centésima más cercana.

Ejercicio$\PageIndex{9}$

$(x−1)^2 = 25$

Responder

x = −4 o x = 6

Ejercicio$\PageIndex{10}$

$(x+3)^2 = 9$

Ejercicio$\PageIndex{11}$

$(x+2)^2 = 0$

Responder

x = −2

Ejercicio$\PageIndex{12}$

$(x−3)^2 = −9$

Ejercicio$\PageIndex{13}$

$(x+6)^2 = −81$

Responder

No hay una solución real

Ejercicio$\PageIndex{14}$

$(x+7)^2 = 10$

Ejercicio$\PageIndex{15}$

$(x−8)^2 = 15$

Responder

$x = 8 \pm \sqrt{15} \approx 4.13, 11.87$

Ejercicio$\PageIndex{16}$

$(x+10)^2 = 37$

En los Ejercicios 17 - 28, realizar cada una de las siguientes tareas para la función cuadrática dada.

1. Configura un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Recuerda dibujar todas las líneas con una regla.
2. Colocar la función cuadrática en forma de vértice. Trazar el vértice en su sistema de coordenadas y etiquetarlo con sus coordenadas. Dibuja el eje de simetría en tu sistema de coordenadas y etiquétalo con su ecuación.
3. Usa la fórmula cuadrática para encontrar las intercepciones x de la parábola. Use una calculadora para aproximar cada intercepción, corrija a la décima más cercana y use estas aproximaciones para trazar las intercepciones x en su sistema de coordenadas. Sin embargo, etiquetar cada intercepción x con sus coordenadas exactas.
4. Trace la intercepción y en su sistema de coordenadas y su imagen especular a través del eje de simetría y etiquete cada uno con sus coordenadas.
5. Usando toda la información de tu sistema de coordenadas, dibuja la gráfica de la parábola, luego etiquétela con la forma de vértice de la función. Utilice la notación de intervalos para indicar el dominio y el rango de la función cuadrática.

Ejercicio$\PageIndex{17}$

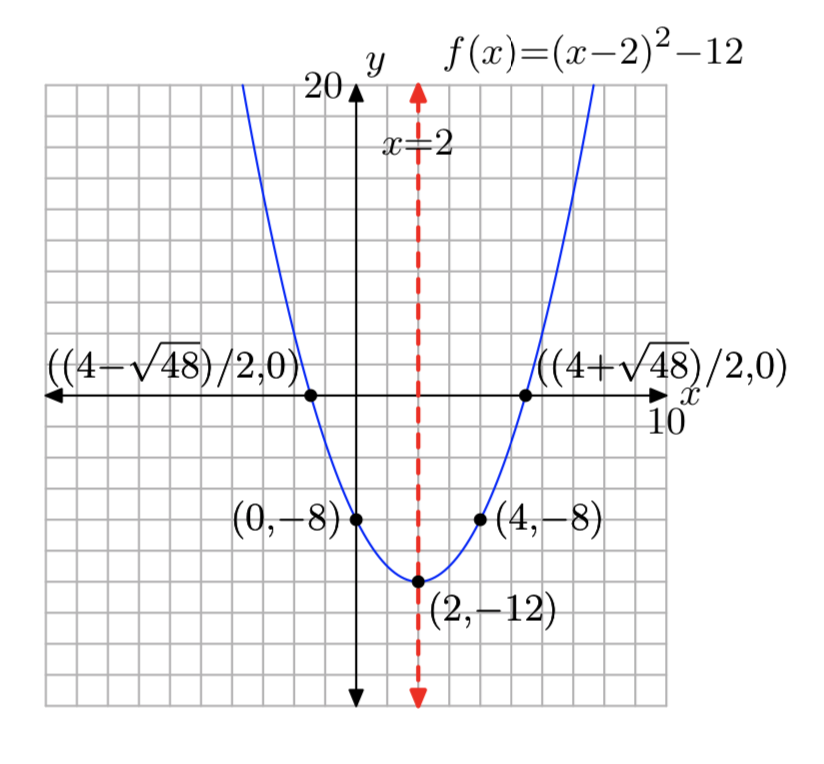
$f(x) = x^2−4x−8$

Responder

Dominio =$(−\infty, \infty)$,

Rango = [−12,$\infty$)

Ejercicio$\PageIndex{18}$

$f(x) = x^2+6x−1$

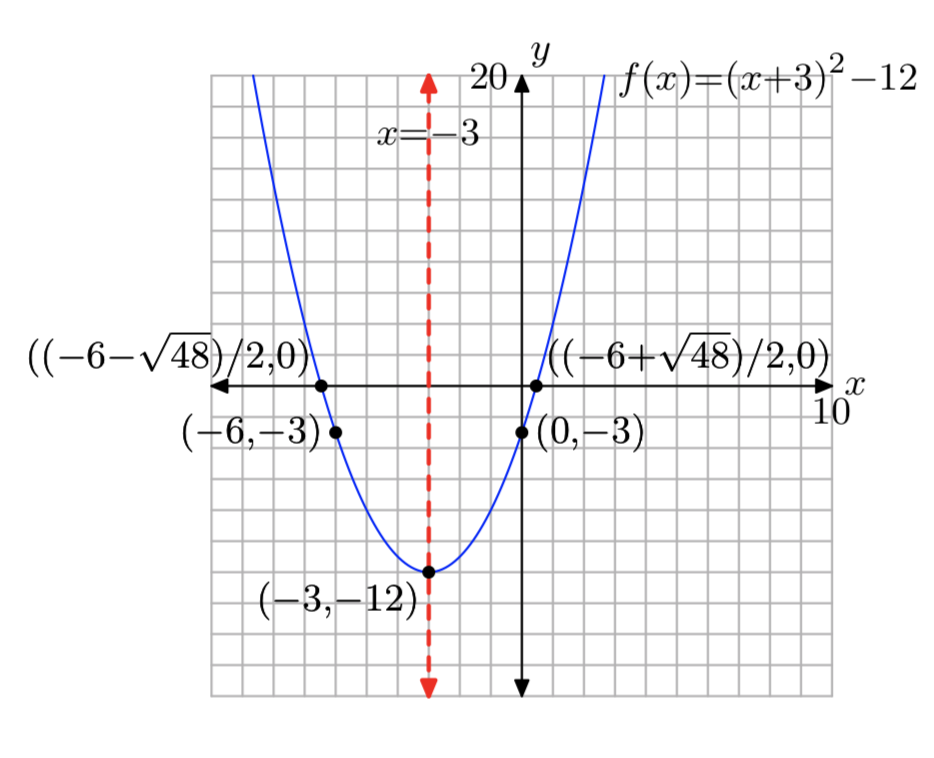
Ejercicio$\PageIndex{19}$

$f(x) = x^2+6x−3$

Responder

Dominio =$(−\infty, \infty)$,

Rango = [−12,$\infty$)

Ejercicio$\PageIndex{20}$

$f(x) = x^2−8x+1$

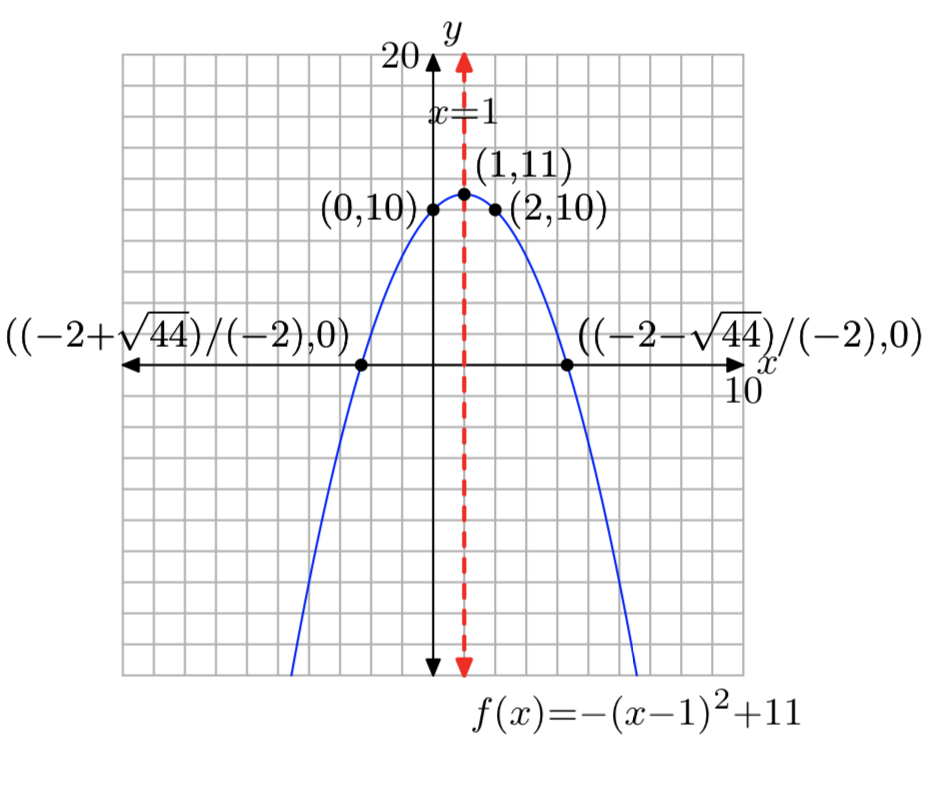
Ejercicio$\PageIndex{21}$

$f(x) = −x^2+2x+10$

Responder

Dominio =$(−\infty, \infty)$,

Rango = (−$\infty$, 11]

Ejercicio$\PageIndex{22}$

$f(x) = −x^2−8x−8$

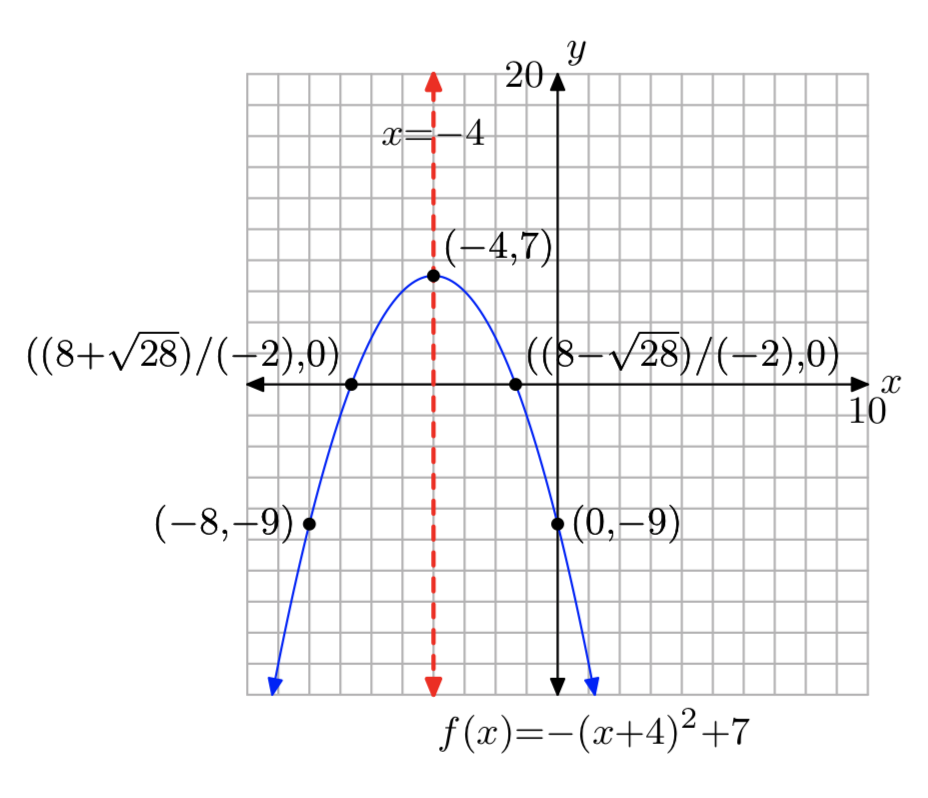
Ejercicio$\PageIndex{23}$

$f(x) = −x^2−8x−9$

Responder

Dominio =$(−\infty, \infty)$,

Rango = (−$\infty$, 7]

Ejercicio$\PageIndex{24}$

$f(x) = −x^2+10x−20$

Ejercicio$\PageIndex{25}$

$f(x)=2x^2−20x+40$

Responder

Dominio =$(−\infty, \infty)$,

Rango = [−10,$\infty$)

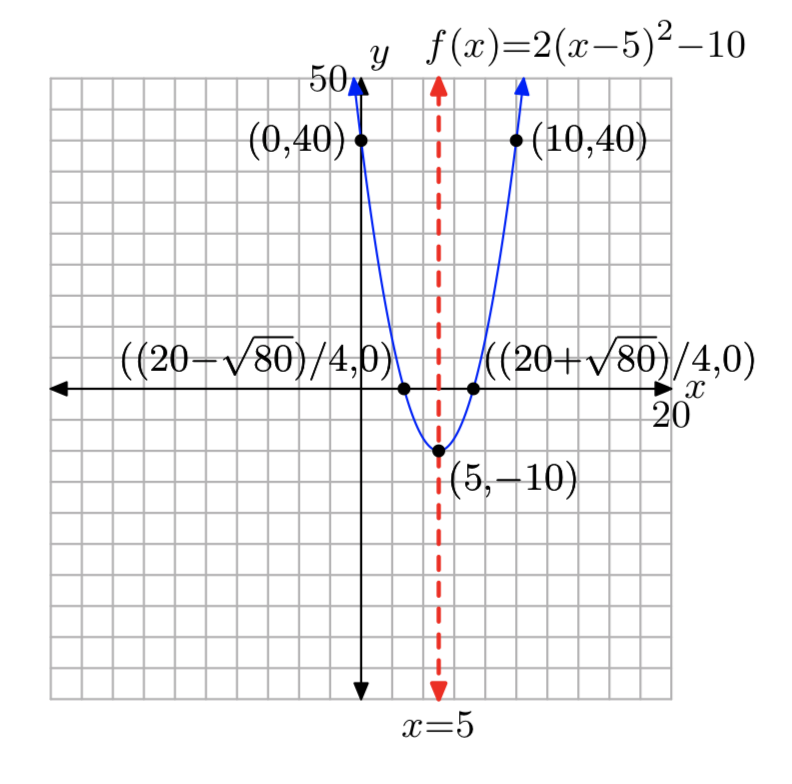
Ejercicio$\PageIndex{26}$

$f(x) = 2x^2−16x+12$

Ejercicio$\PageIndex{27}$

$f(x) = −2x^2+16x+8$

Responder

Dominio =$(−\infty, \infty)$,

Rango = (−$\infty$, 40]

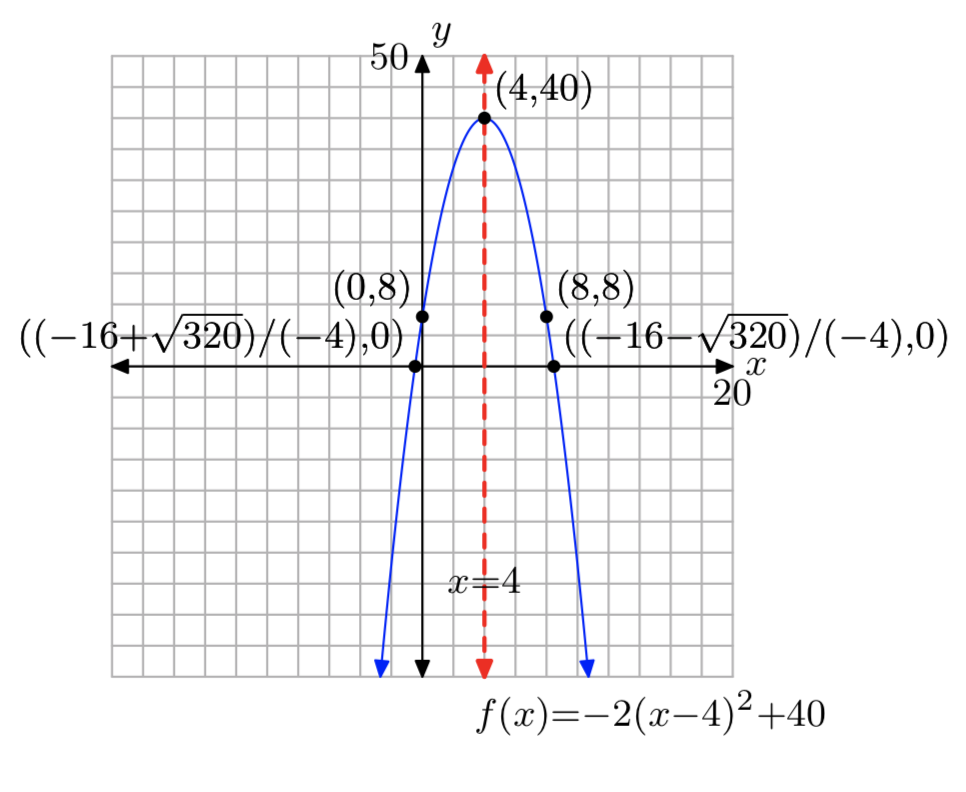
Ejercicio$\PageIndex{28}$

$f(x) = −2x^2−24x−52$

En los Ejercicios 29 - 32, realice cada una de las siguientes tareas para la ecuación cuadrática dada.

1. Configura un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Recuerda dibujar todas las líneas con una regla.
2. Demostrar que el discriminante es negativo.
3. Utiliza la técnica de completar el cuadrado para poner la función cuadrática en forma de vértice. Trazar el vértice en su sistema de coordenadas y etiquetarlo con sus coordenadas. Dibuja el eje de simetría en tu sistema de coordenadas y etiquétalo con su ecuación.
4. Trace la intercepción y y su imagen especular a través del eje de simetría en su sistema de coordenadas y etiquete cada una con sus coordenadas.
5. Porque el discriminante es negativo (¿te acordaste de demostrar eso?) , no hay intercepciones x. Usa la ecuación dada para calcular un punto adicional, luego trazar el punto y su imagen especular a través del eje de simetría y etiquetar cada uno con sus coordenadas.
6. Usando toda la información de tu sistema de coordenadas, dibuja la gráfica de la parábola, luego etiquétela con la forma de vértice de función. Utilice la notación de intervalos para describir el dominio y el rango de la función cuadrática.

Ejercicio$\PageIndex{29}$

$f(x) = x^2+4x+8$

Responder

Dominio =$(−\infty, \infty)$,

Rango = [4,$\infty$)

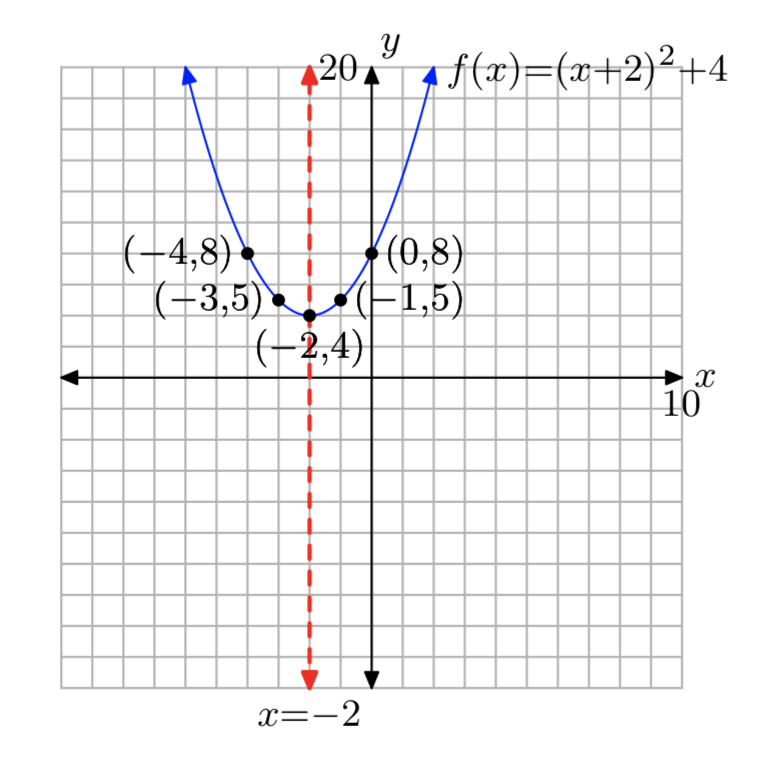
Ejercicio$\PageIndex{30}$

$f(x) = x^2−4x+9$

Ejercicio$\PageIndex{31}$

$f(x) = −x^2+6x−11$

Responder

Dominio =$(−\infty, \infty)$,

Rango = (−$\infty$, −2]

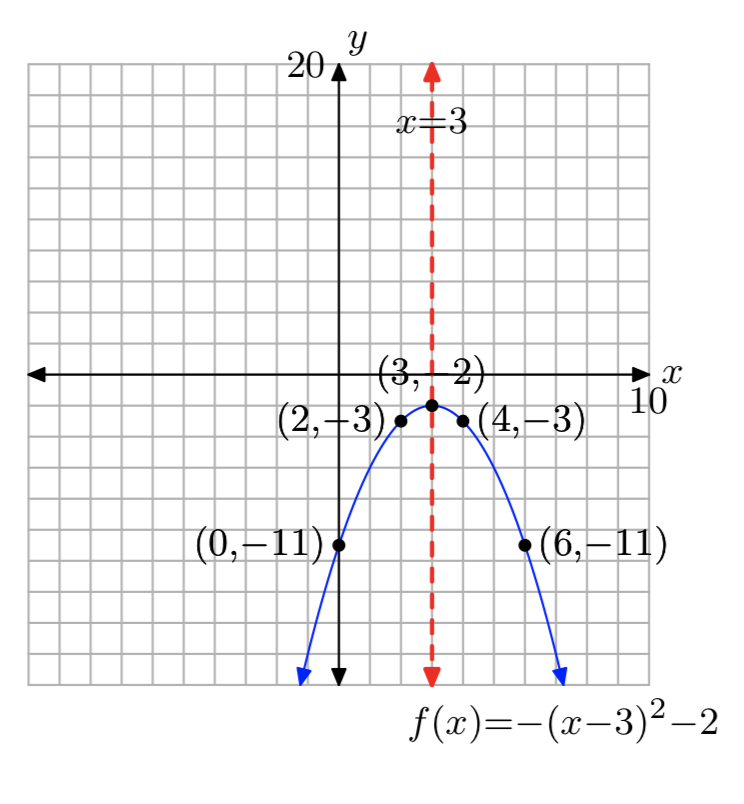
Ejercicio$\PageIndex{32}$

$f(x) = −x^2−8x−20$

En los Ejercicios 33 - 36, realice cada una de las siguientes tareas para la función cuadrática dada.

1. Configura un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Recuerda dibujar todas las líneas con una regla.
2. Utilice el discriminante para ayudar a determinar el valor de k de manera que la gráfica de la función cuadrática dada tenga exactamente una intercepción x.
3. Sustituya este valor de k de nuevo en la función cuadrática dada, luego use la técnica de completar el cuadrado para poner la función cuadrática en forma de vértice. Trazar el vértice en su sistema de coordenadas y etiquetarlo con sus coordenadas. Dibuja el eje de simetría en tu sistema de coordenadas y etiquétalo con su ecuación
4. Trace la intercepción y y su imagen especular a través del eje de simetría y etiquetar cada una con sus coordenadas.
5. Usa la ecuación para calcular un punto adicional a cada lado del eje de simetría, luego traza este punto y su imagen especular a través del eje de simetría y etiquetar cada uno con sus coordenadas.
6. Usando toda la información de tu sistema de coordenadas, dibuja la gráfica de la parábola, luego etiquétela con la forma de vértice de la función. Utilice la notación de intervalos para describir el dominio y el rango de la función cuadrática.

Ejercicio$\PageIndex{33}$

$f(x) = x^2−4x+4k$

Responder

k = 1

Dominio =$(−\infty, \infty)$,

Rango = [0,$\infty$)

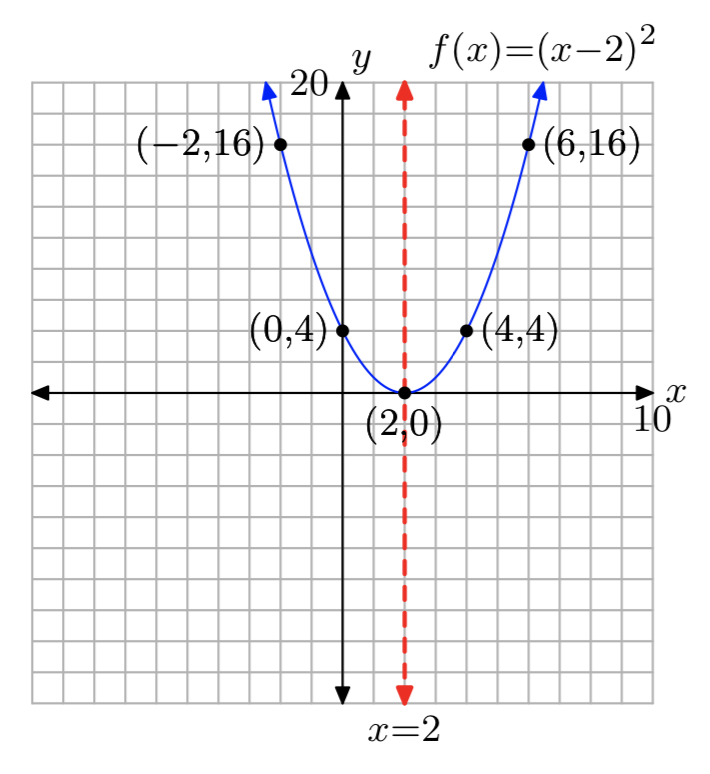
Ejercicio$\PageIndex{34}$

$f(x) = x^2+6x+3k$

Ejercicio$\PageIndex{35}$

$f(x) = kx^2−16x−32$

Responder

k = −2

Dominio =$(−\infty, \infty)$,

Rango = (−$\infty$, 0]

Ejercicio$\PageIndex{36}$

$f(x) = kx^2−24x+48$

Ejercicio$\PageIndex{37}$

Encuentra todos los valores de k para que la gráfica de la función cuadrática$f(x) = kx^2−3x+5$ tenga exactamente dos intercepciones x.

Responder

{k:$k < \frac{9}{20}$}

Ejercicio$\PageIndex{38}$

Encuentra todos los valores de k para que la gráfica de la función cuadrática$f(x) = 2x^2+7x−4k$ tenga exactamente dos intercepciones x.

Ejercicio$\PageIndex{39}$

Encuentra todos los valores de k para que la gráfica de la función cuadrática no$f(x) = 2x^2−x+5k$ tenga intercepciones x.

Responder

{k:$k > \frac{1}{40}$}

Ejercicio$\PageIndex{40}$

Encuentra todos los valores de k para que la gráfica de la función cuadrática no$f(x) = kx^2−2x−4$ tenga intercepciones x.

En los Ejercicios 41 - 50, encuentra todas las soluciones reales, si las hubiere, de la ecuación f (x) = b.

Ejercicio$\PageIndex{41}$

$f(x) = 63x^2+74x−1$; b = 8

Responder

$−\frac{9}{7}, \frac{1}{9}$

Ejercicio$\PageIndex{42}$

$f(x) = 64x^2+128x+64$; b = 0

Ejercicio$\PageIndex{43}$

$f(x) = x^2−x−5$; b = 2

Responder

$\frac{1+\sqrt{29}}{2}, \frac{1−\sqrt{29}}{2}$

Ejercicio$\PageIndex{44}$

$f(x) = 5x^2−5x$; b = 3

Ejercicio$\PageIndex{45}$

$f(x) = 4x^2+4x−1$; b = −2

Responder

$−\frac{1}{2}$

Ejercicio$\PageIndex{46}$

$f(x) = 2x^2−9x−3$; b = −1

Ejercicio$\PageIndex{47}$

$f(x) = 2x^2+4x+6$; b = 0

Responder

no hay soluciones reales

Ejercicio$\PageIndex{48}$

$f(x) = 24x^2−54x+27$; b = 0

Ejercicio$\PageIndex{49}$

$f(x) = −3x^2+2x−13$; b = −5

Responder

no hay soluciones reales

Ejercicio$\PageIndex{50}$

$f(x) = x^2−5x−7$; b = 0

En los Ejercicios 51 - 60, encuentra todas las soluciones reales, si las hubiere, de la ecuación cuadrática.

Ejercicio$\PageIndex{51}$

$−2x^2+7 = −3x$

Responder

$\frac{3−\sqrt{65}}{4}, \frac{3+\sqrt{65}}{4}$

Ejercicio$\PageIndex{52}$

$−x^2 = −9x+7$

Ejercicio$\PageIndex{53}$

$x^2−2 = −3x$

Responder

$−\frac{3−\sqrt{17}}{2}, −\frac{3+\sqrt{17}}{2}$

Ejercicio$\PageIndex{54}$

$81x^2 = −162x−81$

Ejercicio$\PageIndex{55}$

$9x^2+81 = −54x$

Responder

− 3

Ejercicio$\PageIndex{56}$

$−30x^2−28 = −62x$

Ejercicio$\PageIndex{57}$

$−x^2+6 = 7x$

Responder

$−\frac{7+\sqrt{73}}{2}, −\frac{7−\sqrt{73}}{2}$

Ejercicio$\PageIndex{58}$

$−8x^2 = 4x+2$

Ejercicio$\PageIndex{59}$

$4x^2+3 = −x$

Responder

no hay soluciones reales

Ejercicio$\PageIndex{60}$

$27x^2 = −66x+16$

En los Ejercicios 61 - 66, encuentra todas las intercepciones x, si las hay, de la función dada.

Ejercicio$\PageIndex{61}$

$f(x) = −4x^2−4x−5$

Responder

sin intercepciones x

Ejercicio$\PageIndex{62}$

$f(x) = 49x^2−28x+4$

Ejercicio$\PageIndex{63}$

$f(x) = −56x^2+47x+18$

Responder

($\frac{9}{8}$, 0), ($−\frac{2}{7}$, 0)

Ejercicio$\PageIndex{64}$

$f(x) = 24x^2+34x+12$

Ejercicio$\PageIndex{65}$

$f(x) = 36x^2+96x+64$

Responder

($−\frac{4}{3}$, 0)

Ejercicio$\PageIndex{66}$

$f(x) = 5x^2+2x+3$

En los Ejercicios 67 - 74, determinar el número de soluciones reales de la ecuación.

Ejercicio$\PageIndex{67}$

$9x^2+6x+1 = 0$

Responder

1

Ejercicio$\PageIndex{68}$

$7x^2−12x+7 = 0$

Ejercicio$\PageIndex{69}$

$−6x^2+4x−7 = 0$

Responder

0

Ejercicio$\PageIndex{70}$

$−8x^2+11x−4 = 0$

Ejercicio$\PageIndex{71}$

$−5x^2−10x−5 = 0$

Responder

1

Ejercicio$\PageIndex{72}$

$6x^2+11x+2 = 0$

Ejercicio$\PageIndex{73}$

$−7x^2−4x+5 = 0$

Responder

2

Ejercicio$\PageIndex{74}$

$6x^2+10x+4 = 0$

​​​​​​​