6.2: Ceros de polinomios
- Page ID
- 110830
En la sección anterior se estudió el comportamiento final de polinomios. Sabemos que el comportamiento final de un polinomio es idéntico al comportamiento final de su término principal. Nuestro enfoque se concentró en los extremos derecho e izquierdo de la gráfica y no en lo que sucede en el medio. En esta sección, nuestro enfoque se desplaza hacia el interior. Hay dos áreas importantes de concentración: los máximos y mínimos locales del polinomio, y la ubicación de las intercepciones x o ceros del polinomio. En esta sección nos concentramos en encontrar los ceros del polinomio.
Ceros
Comencemos con una definición formal de los ceros de un polinomio.
Definición: Cero del polinomio
\(p(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}\)Sea un polinomio con coeficientes reales. Decimos que\(a\) es un cero del polinomio si y solo si\(p(a) = 0\).
La definición también se mantiene si los coeficientes son complejos, pero ese es un tema para un curso más avanzado.
Por ejemplo, −5 es un cero del polinomio\(p(x)=x^{2}+3 x-10\) porque
\[\begin{aligned} p(-5) &=(-5)^{2}+3(-5)-10 \\ &=25-15-10 \\ &=0 \end{aligned}\]
Del mismo modo, −1 es un cero del polinomio\(p(x)=x^{3}+3 x^{2}-x-3\) porque
\[\begin{aligned} p(-1) &=(-1)^{3}+3(-1)^{2}-(-1)-3 \\ &=-1+3+1-3 \\ &=0 \end{aligned}\]
Veamos un ejemplo más extenso.
Ejemplo\(\PageIndex{1}\)
Encuentra los ceros del polinomio definido por
\[p(x)=(x+3)(x-2)(x-5). \nonumber\]
Solución
A primera vista, la función no parece tener la forma de un polinomio. Sin embargo, dos aplicaciones de la propiedad distributiva proporcionan el producto de los dos últimos factores.
\[\begin{aligned} p(x) &=(x+3)(x(x-5)-2(x-5)) \\ &=(x+3)\left(x^{2}-5 x-2 x+10\right) \\ &=(x+3)\left(x^{2}-7 x+10\right) \end{aligned}\]
Una tercera y cuarta aplicación de la propiedad distributiva revela la naturaleza de nuestra función.
\[\begin{aligned} p(x) &=x\left(x^{2}-7 x+10\right)+3\left(x^{2}-7 x+10\right) \\ &=x^{3}-7 x^{2}+10 x+3 x^{2}-21 x+30 \\ &=x^{3}-4 x^{2}-11 x+30 \end{aligned}\]
De ahí que p sea claramente un polinomio. Sin embargo, la forma factorizada original proporciona un acceso más rápido a los ceros de este polinomio. Usando la Definición 1, necesitamos encontrar valores de x que hagan p (x) = 0. Es decir, tenemos que resolver la ecuación\[p(x)=0\]
Por supuesto, p (x) = (x + 3) (x − 2) (x − 5), entonces, de manera equivalente, necesitamos resolver la ecuación
\[(x+3)(x-2)(x-5)=0\]
Por la propiedad cero del producto, ya sea
\[x+3=0 \quad \text { or } \quad x-2=0 \quad \text { or } \quad x-5=0\]
Se trata de ecuaciones lineales (primer grado), cada una de las cuales se puede resolver de forma independiente. Así, ya sea
\[x=-3 \quad \text { or } \quad x=2 \quad \text { or } \quad x=5\]
De ahí que los ceros del polinomio p son −3, 2 y 5.
Usemos la ecuación (4) para verificar que −3 es un cero del polinomio p. Sustituya −3 por x in\(p(x)=x^{3}-4 x^{2}-11 x+30\).
\[\begin{aligned} p(-3) &=(-3)^{3}-4(-3)^{2}-11(-3)+30 \\ &=-27-36+33+30 \\ &=0 \end{aligned}\]
Este cálculo verifica que −3 es un cero del polinomio p. Sin embargo, es mucho más fácil verificar que −3 es un cero del polinomio usando la ecuación (3). Sustituye −3 por x en p (x) = (x + 3) (x − 2) (x − 5).
\[\begin{aligned} p(-3) &=(-3+3)(-3-2)(-3-5) \\ &=(0)(-5)(-8) \\ &=0 \end{aligned}\]
Dejaremos a nuestros lectores comprobar que 2 y 5 son también ceros del polinomio p.
Es muy importante tener en cuenta que una vez que conoces los factores lineales (primer grado) de un polinomio, los ceros siguen con facilidad. En el último ejemplo, p (x) = (x+3) (x−2) (x−5), por lo que los factores lineales son x + 3, x − 2 y x − 5. En consecuencia, los ceros son −3, 2 y 5.
Antes de continuar, nos tomamos un momento para revisar un patrón de multiplicación importante.
La diferencia de dos cuadrados
Un patrón especial de multiplicación que aparece frecuentemente en este texto se llama la diferencia de dos cuadrados. Utilice la propiedad distributiva para expandir (a + b) (a − b).
\[\begin{aligned}(a+b)(a-b) &=a(a-b)+b(a-b) \\ &=a^{2}-a b+b a-b^{2} \end{aligned}\]
Ya que\(ab = ba\), tenemos el siguiente resultado.
Propiedad 5: La diferencia del patrón de dos cuadrados
\[(a+b)(a-b)=a^{2}-b^{2}\]
Así, si tienes dos binomios con idénticos términos primero y segundo, pero los términos de uno están separados por un signo más, mientras que los términos del segundo están separados por un signo menos, entonces multiplicas al cuadrado el primer y segundo términos y separando estos cuadrados con un signo menos. De ahí el nombre, la “diferencia de dos cuadrados”.
Por ejemplo,
\[(2 x+3)(2 x-3)=(2 x)^{2}-(3)^{2}=4 x^{2}-9 \nonumber\]
Observe cómo simplemente cuadramos los términos primero y segundo coincidentes y luego separamos nuestros cuadrados con un signo menos. De manera similar,
\[\begin{aligned}(x+5)(x-5) &=x^{2}-25 \\(5 x+4)(5 x-4) &=25 x^{2}-16 \\(3 x-7)(3 x+7) &=9 x^{2}-49 \end{aligned}\]
En cada caso, observe cómo cuadramos los términos primero y segundo coincidentes, luego separamos los cuadrados con un signo menos.
Una vez que hayas dominado la multiplicación usando el patrón “Diferencia de cuadrados”, es fácil factorizar usando el mismo patrón. Simplemente revierte el procedimiento. Por ejemplo
\[4 x^{2}-9=(2 x+3)(2 x-3) \nonumber\]
Empezamos por tomar la raíz cuadrada de las dos plazas. Así, la raíz cuadrada de 4\(x^{2}\) es 2x y la raíz cuadrada de 9 es 3. Luego formamos dos binomios con los resultados 2x y 3 como términos coincidentes primero y segundo, separando un par con un signo más, el otro par con un signo menos.
De manera similar,\[9 x^{2}-49=(3 x+7)(3 x-7) \nonumber\]
Nuevamente, observe cómo tomamos la raíz cuadrada de cada término, formamos dos binomios con los resultados, luego separamos un par con un plus, el otro con un menos.
Encontraremos a mano el patrón “Diferencia de cuadrados” en lo que sigue.
Encontrar ceros por factorización
Ahora exploraremos cómo podemos encontrar los ceros de un polinomio mediante factorización, seguido de la aplicación de la propiedad cero del producto. Es importante entender que los polinomios de esta sección han sido cuidadosamente seleccionados para que los puedas factorizar utilizando las diversas técnicas que siguen.
Exploremos factorización por agrupación.
Ejemplo\(\PageIndex{2}\)
Encuentra los ceros del polinomio\[p(x)=x^{3}+2 x^{2}-25 x-50\]
Solución
En Ejemplo\(\PageIndex{1}\) aprendimos que es fácil detectar los ceros de un polinomio si el polinomio se expresa como un producto de factores lineales (primer grado). En este ejemplo no se factoriza el polinomio, por lo que parecería que lo primero que tendremos que hacer es factorizar nuestro polinomio.
Siempre que se te presente una expresión de cuatro términos, una cosa que puedes probar es factorizar agrupando. Entonces, con este pensamiento en mente, vamos a factorizar una x de los dos primeros términos, luego un −25 de los dos segundos términos.
\[\begin{aligned} p(x) &=x^{3}+2 x^{2}-25 x-50 \\ &=x^{2}(x+2)-25(x+2) \end{aligned}\]
Obsérvese que este último resultado es la diferencia de dos términos. El polinomio aún no está completamente factorizado ya que aún no es producto de dos o más factores. No obstante, tenga en cuenta que cada uno de los dos términos tiene un factor común de x + 2. Vamos a factorizar este factor común.
\[p(x)=\left(x^{2}-25\right)(x+2)\]
Todavía no hemos factorizado completamente nuestro polinomio. El primer factor es la diferencia de dos cuadrados y se puede factorizar aún más.
\[p(x)=(x+5)(x-5)(x+2)\]
El polinomio p ahora está completamente factorizado. Para encontrar los ceros del polinomio p, necesitamos resolver la ecuación\[p(x)=0\]
Sin embargo, p (x) = (x + 5) (x − 5) (x + 2), así que de manera equivalente, necesitamos resolver la ecuación\[(x+5)(x-5)(x+2)=0\]
Podemos usar la propiedad cero del producto. O\[x+5=0 \quad \text { or } \quad x-5=0 \quad \text { or } \quad x+2=0\]
Nuevamente, cada una de estas ecuaciones lineales (primer grado) se puede resolver de forma independiente. O\[x=-5 \quad \text { or } \quad x=5 \quad \text { or } \quad x=-2\]
Así, los ceros del polinomio p son −5, 5 y −2. Dejaremos que nuestros lectores verifiquen estos resultados.
Nuevamente, es muy importante darse cuenta de que una vez determinados los factores lineales (primer grado), siguen los ceros del polinomio. En este ejemplo, los factores lineales son x + 5, x − 5 y x + 2. Inmediatamente se deduce que los ceros del polinomio son −5, 5 y −2.
En el siguiente ejemplo, veremos que a veces el primer paso es factorizar el mayor factor común.
Ejemplo\(\PageIndex{3}\)
Encuentra los ceros del polinomio\[p(x)=x^{4}+2 x^{3}-16 x^{2}-32 x\]
Solución
Para encontrar los ceros del polinomio, necesitamos resolver la ecuación\[p(x)=0\]
Equivalentemente\(p(x)=x^{4}+2 x^{3}-16 x^{2}-32 x\), porque, necesitamos resolver la ecuación
\[x^{4}+2 x^{3}-16 x^{2}-32 x=0\]
Tenga en cuenta que cada término del lado izquierdo tiene un factor común de x. Así, nuestro primer paso es factorizar este factor común de x.
\[x\left[x^{3}+2 x^{2}-16 x-32\right]=0\]
La expresión de cuatro términos dentro de los corchetes parece familiar. Intentemos factorizar agrupando. \(x^2\)Factorizar un de los dos primeros términos, luego un −16 del tercer y cuarto términos.
\[x\left[x^{2}(x+2)-16(x+2)\right]=0\]
Ahora tenemos un factor común de x + 2, así que lo factorizamos.
\[x\left[\left(x^{2}-16\right)(x+2)\right]=0\]
Los corchetes ya no son necesarios (la multiplicación es asociativa) así que los dejamos apagados, luego usamos la diferencia de cuadrados patrón a factor\(x^2 − 16\).
\[x(x+4)(x-4)(x+2)=0\]
La propiedad cero del producto nos dice que
\[x=0 \quad \text { or } \quad \text { or } \quad x+4=0 \quad \text { or } \quad x-4=0 \quad \text { or } \quad \text { or } \quad x+2=0\]
Cada uno de estos factores lineales (primer grado) se pueden resolver de forma independiente. O bien
\[x=0 \quad \text { or } \quad x=-4 \quad \text { or } \quad x=4 \quad \text { or } \quad x=-2\]
Así, los ceros del polinomio p son 0, −4, 4 y −2. Dejaremos que nuestros lectores verifiquen estos resultados.
Nuevamente, es muy importante señalar que una vez que hayas determinado los factores lineales (primer grado) de un polinomio, entonces conoces los ceros. En este caso, los factores lineales son x, x + 4, x − 4 y x + 2. Por lo tanto, los ceros son 0, −4, 4 y −2, respectivamente. Esta discusión lleva a un resultado llamado Teorema de Factores.
Teorema de factores
\(p(x)=a_{0}+a_{1} x+a_{2} x^{2}+\ldots+a_{n} x^{n}\)Sea un polinomio con coeficientes reales. Si x − a es un factor del polinomio p (x), entonces a es un cero del polinomio. Es decir, si x − a es un factor del polinomio p (x), entonces p (a) = 0.
El resultado de todas estas observaciones es el hecho de que, si conoces los factores lineales del polinomio, entonces conoces los ceros. Lo contrario también es cierto, pero no lo necesitaremos en este curso.
Examinemos la conexión entre los ceros del polinomio y las intercepciones x de la gráfica del polinomio.
Las intercepciones x y los ceros de un polinomio
Para la discusión que sigue, supongamos que la variable independiente es x y la variable dependiente es y. Correspondiendo a estas asignaciones, también asumiremos que hemos etiquetado el eje horizontal con x y el eje vertical con y, como se muestra en la Figura\(\PageIndex{1}\).
El dato clave para el resto de esta sección es que una función es cero en los puntos donde su gráfica cruza el eje x. Las frases “valores de función” e “valores y” son equivalentes (siempre que su variable dependiente sea y), así que cuando se le pregunte dónde su valor de función es igual a cero, en realidad se le pregunta “¿dónde es su valor y igual a cero?” Por supuesto, y = 0 donde la gráfica de la función cruza el eje horizontal (nuevamente, siempre que esté usando la letra y para su variable dependiente, etiquetando el eje vertical con y).
Un polinomio es una función, entonces, como cualquier función, un polinomio es cero donde su gráfica cruza el eje horizontal. Como se puede ver en la Figura\(\PageIndex{1}\), la gráfica del polinomio cruza el eje horizontal en x = −6, x = 1, y x = 5. Tenga en cuenta que en cada una de estas intercepciones, el valor y (valor de función) es igual a cero. Los ceros del polinomio son −6, 1 y 5. Por lo tanto, las intercepciones x de la gráfica del polinomio se localizan en (−6, 0), (1, 0) y (5, 0).
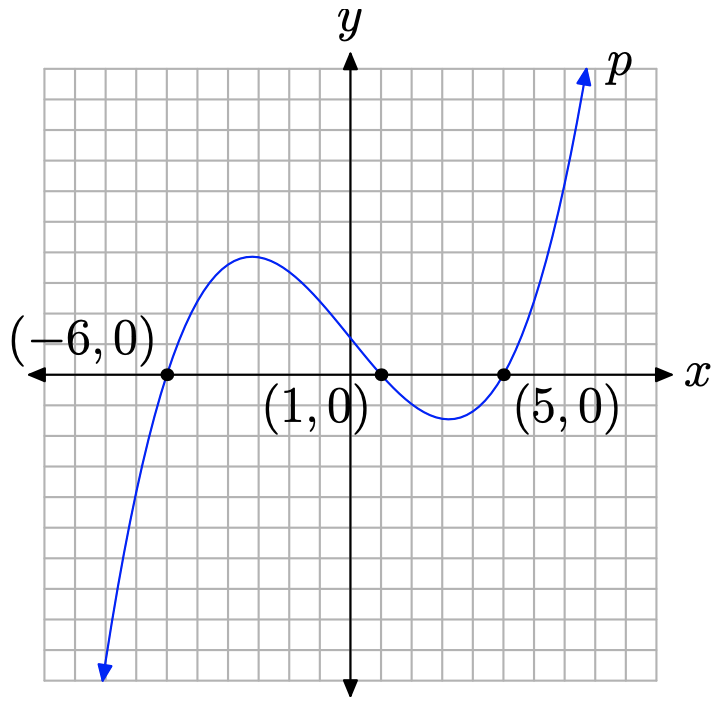
Usemos estas ideas para trazar las gráficas de varios polinomios.
Ejemplo\(\PageIndex{4}\)
Esbozar la gráfica del polinomio en Ejemplo\(\PageIndex{2}\).
Solución
En Ejemplo\(\PageIndex{2}\), el polinomio\(p(x)=x^{3}+2 x^{2}-25 x-50\) factorizado en factores lineales\[p(x)=(x+5)(x-5)(x+2)\]
En consecuencia, los ceros del polinomio fueron −5, 5 y −2. Así, las intercepciones x de la gráfica del polinomio se localizan en (−5, 0), (5, 0) y (−2, 0).
El polinomio\(p(x)=x^{3}+2 x^{2}-25 x-50\) tiene término principal\(x^3\). En consecuencia, a medida que balanceamos nuestros ojos de izquierda a derecha, la gráfica del polinomio p debe elevarse desde el infinito negativo, menear a través de sus intercepciones x, luego continuar elevándose hasta el infinito positivo. No tenemos más remedio que bosquejar una gráfica similar a la de la Figura\(\PageIndex{2}\).
Obsérvese que hay dos “puntos de inflexión” del polinomio en la Figura\(\PageIndex{2}\). Podría preguntarse cómo sabíamos dónde poner estos “puntos de inflexión” del polinomio. La respuesta es “no sabíamos dónde ponerlos”. Sabemos que tienen que estar ahí, pero no sabemos su ubicación precisa. Por eso no hemos escalado el eje vertical, pues sin la ayuda de una calculadora, es difícil determinar la ubicación precisa de los puntos de inflexión mostrados en la Figura\(\PageIndex{2}\).
Sin embargo, tenga en cuenta que el conocimiento del comportamiento final y los ceros del polinomio nos permite construir un facsímil razonable de la gráfica real. Si queremos más precisión de la que proporciona una aproximación aproximada, como la precisión que se muestra en la Figura\(\PageIndex{2}\), tendremos que usar nuestra calculadora gráfica, como se demuestra en la Figura\(\PageIndex{3}\).
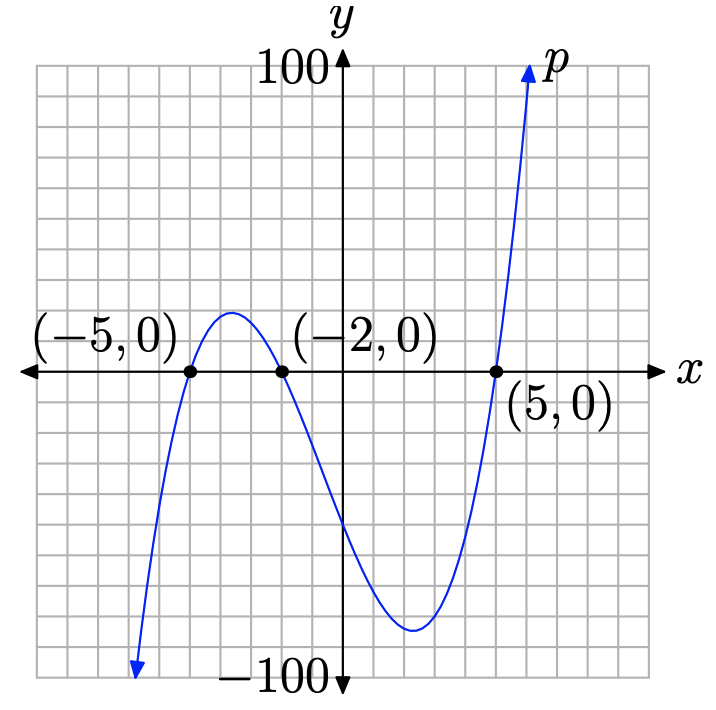
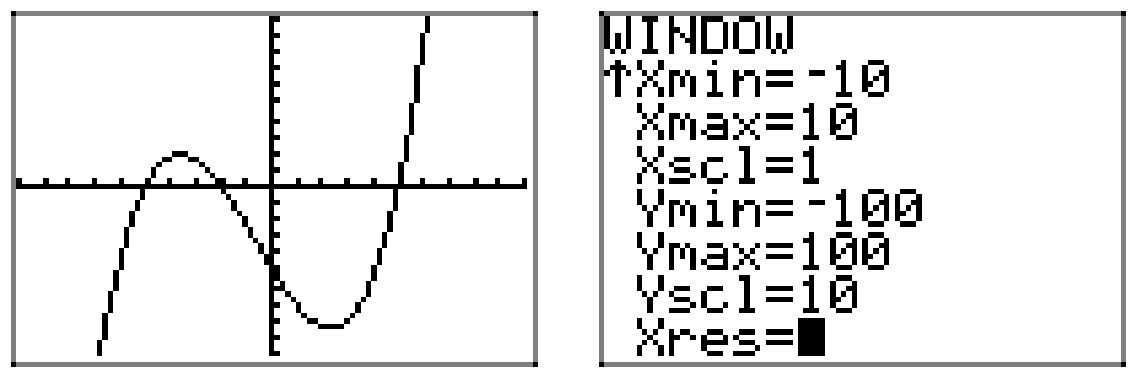
Tendremos más que decir sobre los “puntos de inflexión” (extremos relativos) en la siguiente sección. Por ahora, sigamos enfocándonos en el comportamiento final y los ceros.
Veamos otro ejemplo.
Ejemplo\(\PageIndex{5}\)
Esbozar la gráfica del polinomio en Ejemplo\(\PageIndex{3}\).
Solución
En Ejemplo\(\PageIndex{3}\), el polinomio\(p(x)=x^{4}+2 x^{3}-16 x^{2}-32 x\) factorizado en un producto de factores lineales
\[p(x)=x(x+4)(x-4)(x+2)\]
En consecuencia, los ceros del polinomio son 0, −4, 4 y −2. Así, las intercepciones x de la gráfica del polinomio se localizan en (0, 0), (−4, 0), (4, 0) y (−2, 0).
El polinomio\(p(x)=x^{4}+2 x^{3}-16 x^{2}-32 x\) tiene término principal\(x^4\). En consecuencia, a medida que balanceamos nuestros ojos de izquierda a derecha, la gráfica del polinomio p debe caer desde el infinito positivo, menearse a través de sus intercepciones x, luego elevarse de nuevo al infinito positivo. No tenemos más remedio que bosquejar una gráfica similar a la de la Figura\(\PageIndex{4}\).
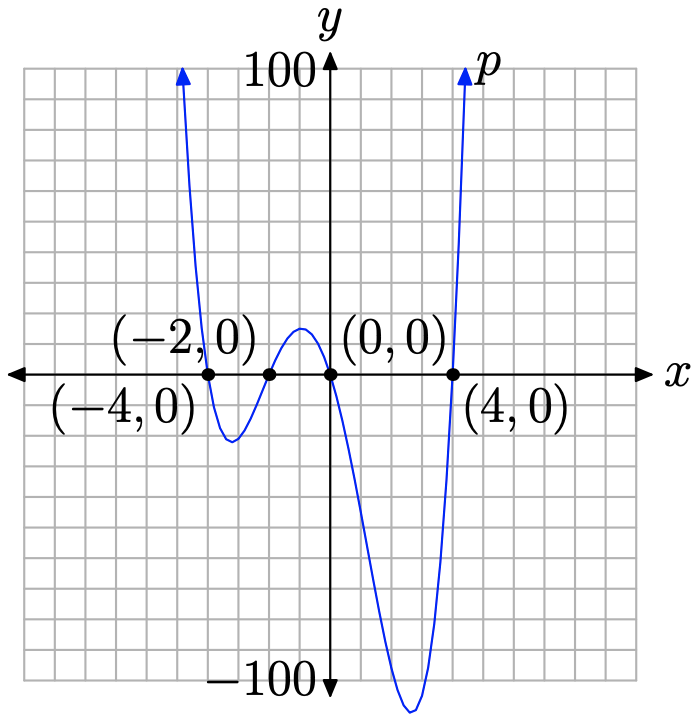
Nuevamente, podemos dibujar un boceto de la gráfica sin el uso de la calculadora, utilizando únicamente el comportamiento final y ceros del polinomio. Sin embargo, si queremos la precisión representada en la Figura\(\PageIndex{4}\), particularmente para encontrar ubicaciones correctas de los “puntos de inflexión”, tendremos que recurrir al uso de una calculadora gráfica. Esto se muestra en la Figura\(\PageIndex{5}\).
Veamos un ejemplo final que requiere factorizar un mayor factor común seguido de la prueba ac.
Ejemplo\(\PageIndex{6}\)
Encuentra los ceros del polinomio\[p(x)=4 x^{3}-2 x^{2}-30 x\]
Solución
Primero, observe que cada término de este trinomio es divisible por 2x. Este es el mayor divisor común, o equivalentemente, el mayor factor común. Siempre debes buscar factorizar el mayor factor común en tu primer paso.
\[\begin{aligned} p(x) &=4 x^{3}-2 x^{2}-30 x \\ &=2 x\left[2 x^{2}-x-15\right] \end{aligned}\]
A continuación, compare el trinomio\(2 x^{2}-x-15\) con\(a x^{2}+b x+c\) y observe que ac = −30. El par entero {5, −6} tiene el producto −30 y la suma −1. Reescribir el término medio de\(2 x^{2}-x-15\) en términos de este par y factorizar por agrupación.
\[\begin{aligned} p(x) &=2 x\left[2 x^{2}+5 x-6 x-15\right] \\ &=2 x[x(2 x+5)-3(2 x+5)] \\ &=2 x(x-3)(2 x+5) \end{aligned}\]
Para encontrar los ceros, necesitamos resolver la ecuación polinómica p (x) = 0, o equivalentemente,
\[2 x(x-3)(2 x+5)=0\]
Usando la propiedad cero del producto, ya sea
\[2 x=0, \quad \text { or } \quad x-3=0, \quad \text { or } \quad 2 x+5=0\]
Cada uno de estos factores lineales se puede resolver de forma independiente. Así, ya sea
\[x=0, \quad \text { or } \quad x=3, \quad \text { or } \quad x=-\frac{5}{2}\]
Así, los ceros del polinomio son 0, 3 y −5/2.
Alternativamente, se puede factorizar un 2 del tercer factor en la ecuación (12).
\[\begin{aligned} p(x) &=2 x(x-3)(2)\left(x+\frac{5}{2}\right) \\ &=4 x(x-3)\left(x+\frac{5}{2}\right) \end{aligned}\]
En esta forma,
- x es un factor, entonces x = 0 es un cero,
- x − 3 es un factor, entonces x = 3 es un cero, y
- x + 5/2 es un factor, entonces x = −5/2 es un cero.
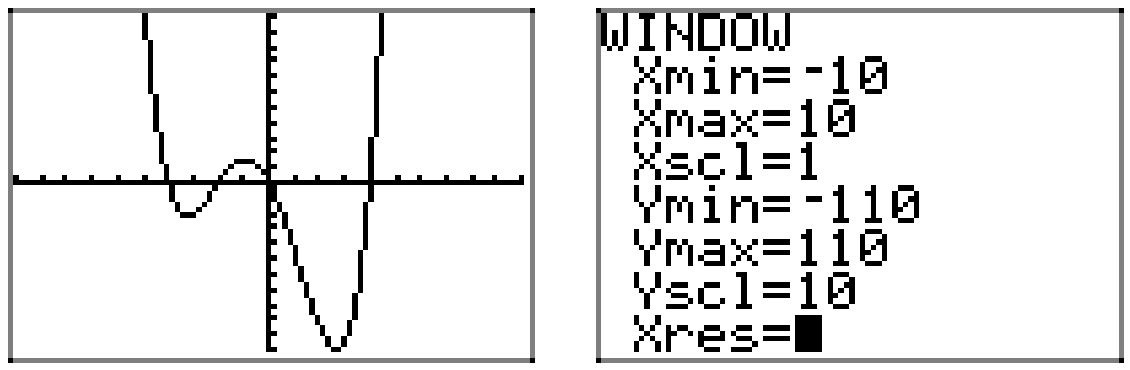
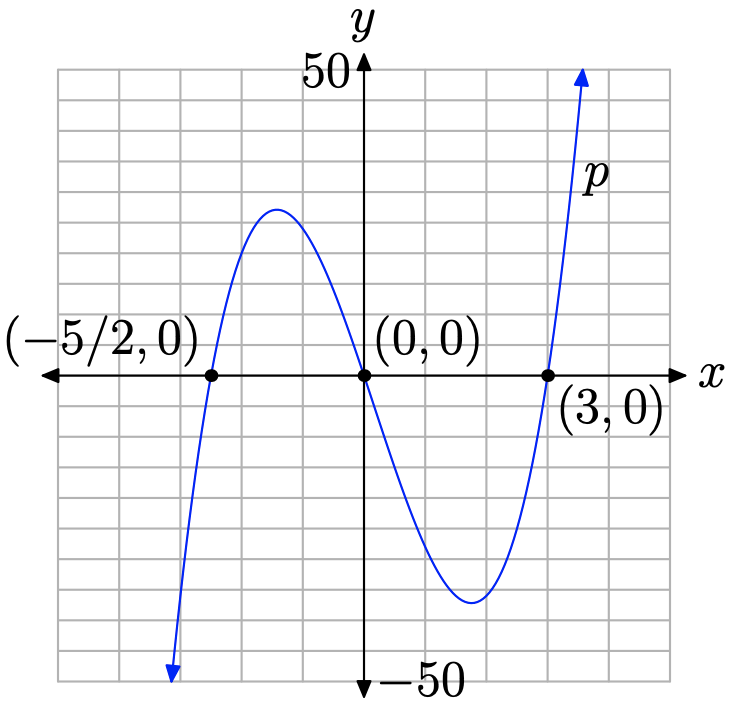
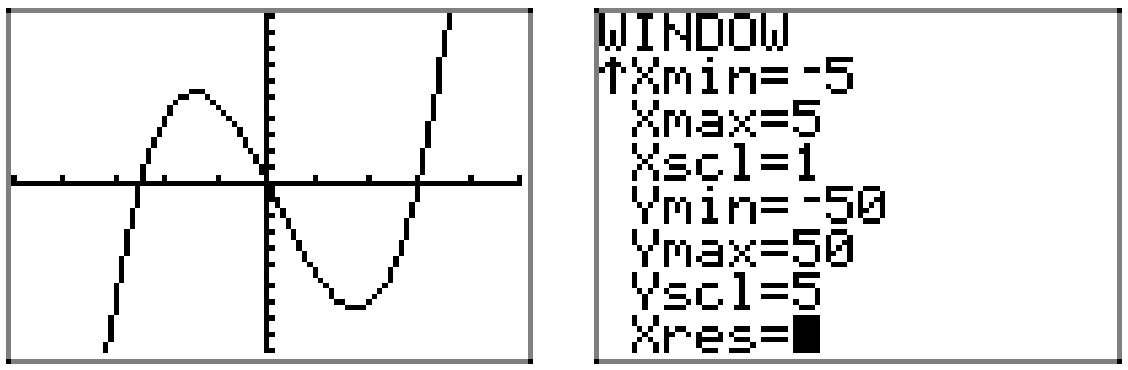
El término principal de\(p(x)=4 x^{3}-2 x^{2}-30 x\) es 4\(x^{2}\), así como nuestros ojos oscilan de izquierda a derecha, la gráfica del polinomio debe elevarse desde el infinito negativo, menear a través de sus ceros, luego elevarse al infinito positivo. Por lo tanto, la gráfica debe ser similar a la que se muestra en la Figura\(\PageIndex{6}\).
Nuevamente, las intercepciones y el comportamiento final proporcionan amplias pistas sobre la forma de la gráfica, pero, si queremos que la precisión retratada en la Figura 6, entonces debemos confiar en la calculadora gráfica. La gráfica y los ajustes de ventana utilizados se muestran en la Figura\(\PageIndex{7}\).
Ejercicio
En los Ejercicios 1 - 6, utilice la sustitución directa para mostrar que el valor dado es un cero del polinomio dado.
Ejercicio\(\PageIndex{1}\)
\(p(x) = x^3−3x^2−13x+15\), x = −3
- Contestar
-
p (−3) = (−3) 3−3 (−3) 2−13 (−3) +15 = 0
Ejercicio\(\PageIndex{2}\)
\(p(x) = x^3−2x^2−13x−10\), x = −2
Ejercicio\(\PageIndex{3}\)
\(p(x) = x^4−x^3−12x^2\), x = 4
- Contestar
-
\(p(4) = 4^4−4^3−12(4)^2 = 0\)
Ejercicio\(\PageIndex{4}\)
\(p(x) = x^4−2x^3−3x^2\), x = −1
Ejercicio\(\PageIndex{5}\)
\(p(x) = x^4+x^2−20\), x = −2
- Contestar
-
\(p(−2) = (−2)^4+(−2)^2−20 = 0\)
Ejercicio\(\PageIndex{6}\)
\(p(x) = x^4+x^3−19x^2+11x+30\), x = −1
En los Ejercicios 7 - 28, identificar todos los ceros del polinomio dado sin la ayuda de una calculadora. Utilizar una técnica algebraica y mostrar todo el trabajo (factor cuando sea necesario) necesario para obtener los ceros.
Ejercicio\(\PageIndex{7}\)
p (x) = (x−2) (x+4) (x−5)
- Contestar
-
− 4, 2 y 5
Ejercicio\(\PageIndex{8}\)
p (x) = (x−1) (x−3) (x+8)
Ejercicio\(\PageIndex{9}\)
p (x) = −2 (x−3) (x+4) (x−2)
- Contestar
-
− 4, 2 y 3
Ejercicio\(\PageIndex{10}\)
p (x) = −3 (x+1) (x−1) (x−8)
Ejercicio\(\PageIndex{11}\)
p (x) = x (x−3) (2x+1)
- Contestar
-
\(−\frac{1}{2}\), 0 y 3
Ejercicio\(\PageIndex{12}\)
p (x) = −3x (x+5) (3x−2)
Ejercicio\(\PageIndex{13}\)
p (x) = −2 (x+3) (3x−5) (2x+1)
- Contestar
-
−3,\(−\frac{1}{2}\), y\(\frac{5}{3}\)
Ejercicio\(\PageIndex{14}\)
p (x) = 3 (x−2) (2x+5) (3x−4)
Ejercicio\(\PageIndex{15}\)
\(p(x) = 3x^3+5x^2−12x−20\)
- Contestar
-
−2\(−\frac{5}{3}\), y 2
Ejercicio\(\PageIndex{16}\)
\(p(x) = 3x^3+x^2−12x−4\)
Ejercicio\(\PageIndex{17}\)
\(p(x) = 2x^3+5x^2−2x−5\)
- Contestar
-
\(−\frac{5}{2}\), −1 y 1
Ejercicio\(\PageIndex{18}\)
\(p(x) = 2x^3−5x^2−18x+45\)
Ejercicio\(\PageIndex{19}\)
\(p(x) = x^4+4x^3−9x^2−36x\)
- Contestar
-
0, −3, 3 y −4
Ejercicio\(\PageIndex{20}\)
\(p(x) = −x^4+4x^3+x^2−4x\)
Ejercicio\(\PageIndex{21}\)
\(p(x) = −2x^4−10x^3+8x^2+40x\)
- Contestar
-
0, −2, 2 y −5
Ejercicio\(\PageIndex{22}\)
\(p(x) = 3x^4+6x^3−75x^2−150x\)
Ejercicio\(\PageIndex{23}\)
\(p(x) = 2x^3−7x^2−15x\)
- Contestar
-
\(−\frac{3}{2}\), 0 y 5
Ejercicio\(\PageIndex{24}\)
\(p(x) = 2x^3−x^2−10x\)
Ejercicio\(\PageIndex{25}\)
\(p(x) = −6x^3+4x^2+16x\)
- Contestar
-
\(−\frac{4}{3}\), 0 y 2
Ejercicio\(\PageIndex{26}\)
\(p(x) = 9x^3+3x^2−30x\)
Ejercicio\(\PageIndex{27}\)
\(p(x) = −2x^7−10x^6+8x^5+40x^4\)
- Responder
-
0, −2, 2 y −5
Ejercicio\(\PageIndex{28}\)
\(p(x) = 6x^5−21x^4−45x^3\)
En los Ejercicios 29 - 34 se da la gráfica de un polinomio. Realizar cada una de las siguientes tareas
- Copia la imagen en tu papel de tarea. Etiquete y escale sus ejes, luego etiquete cada intercepción x con sus coordenadas.
- Identificar los ceros del polinomio.
Ejercicio\(\PageIndex{29}\)
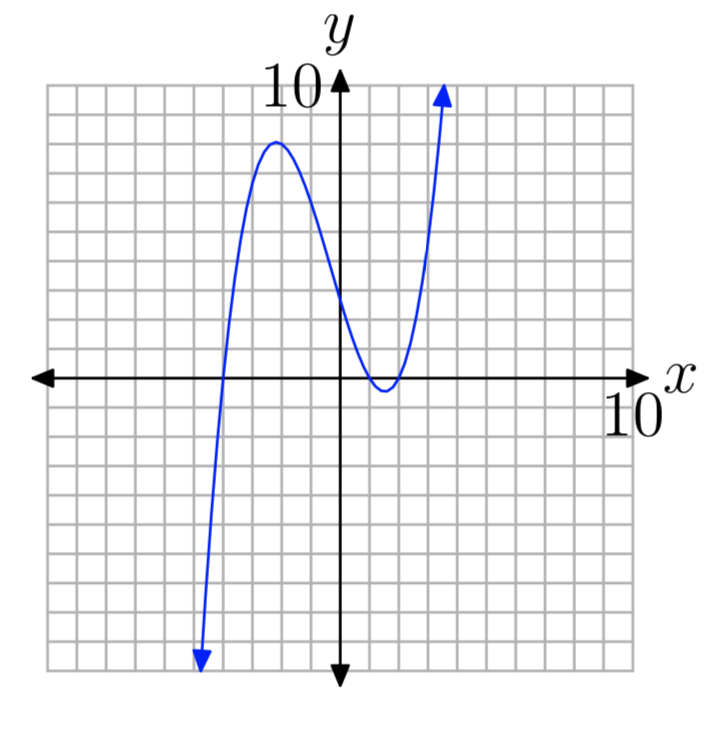
- Responder
-
Ceros: −4, 1 y 2
Ejercicio\(\PageIndex{30}\)
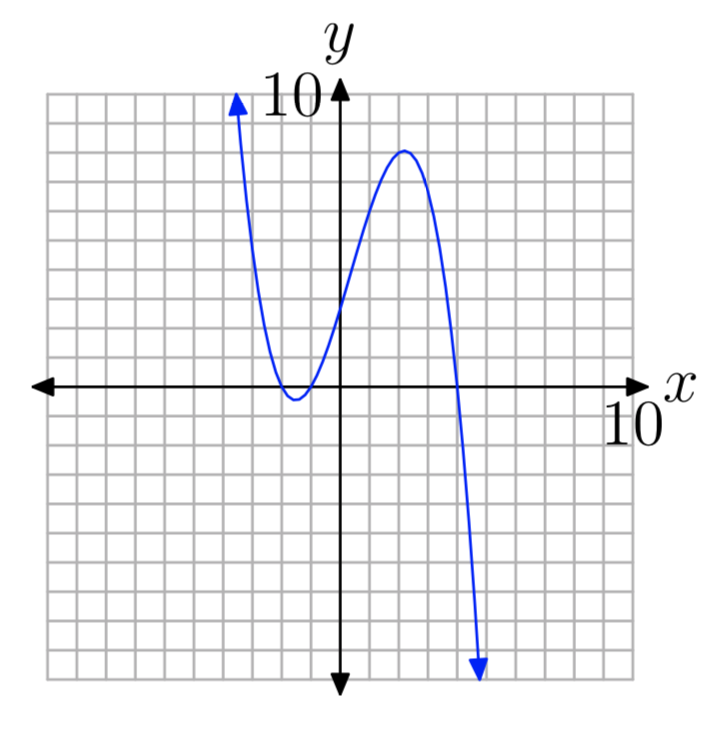
Ejercicio\(\PageIndex{31}\)
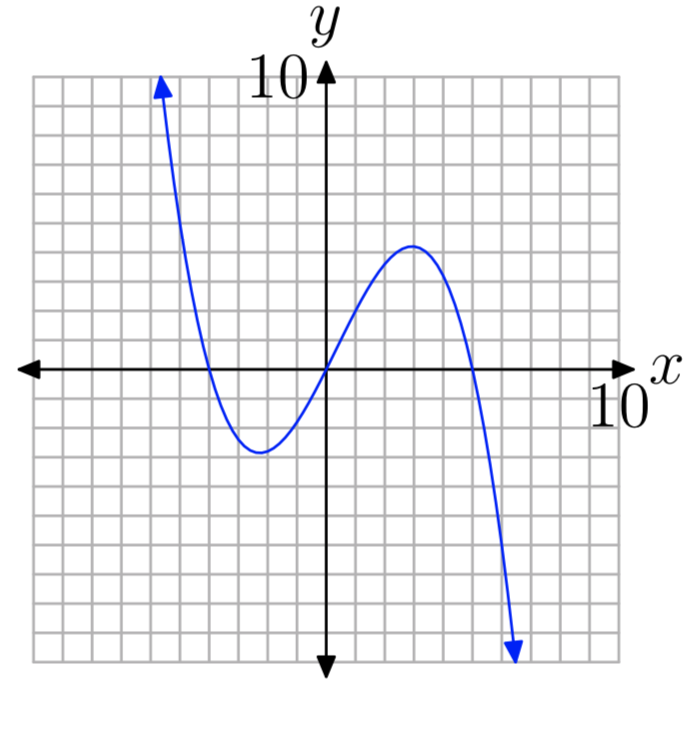
- Responder
-
Ceros: − 4, 0 y 5
Ejercicio\(\PageIndex{32}\)
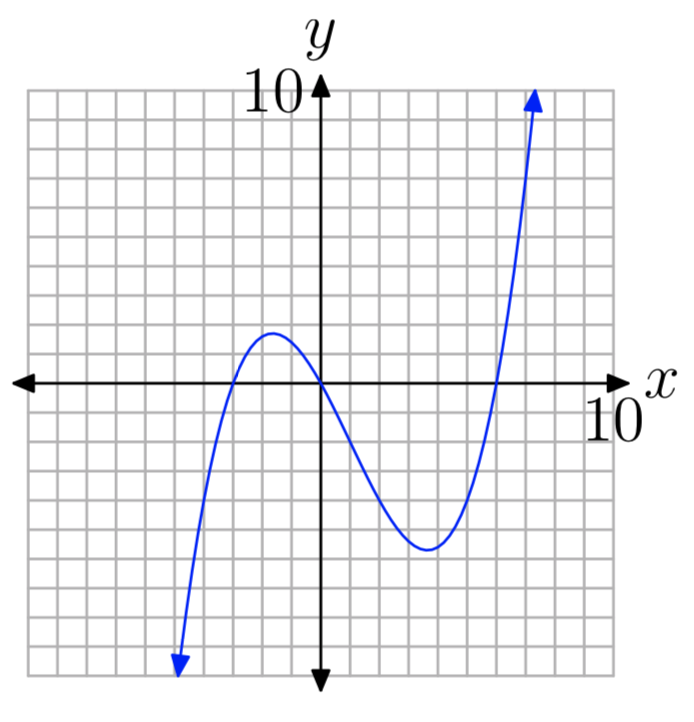
Ejercicio\(\PageIndex{33}\)
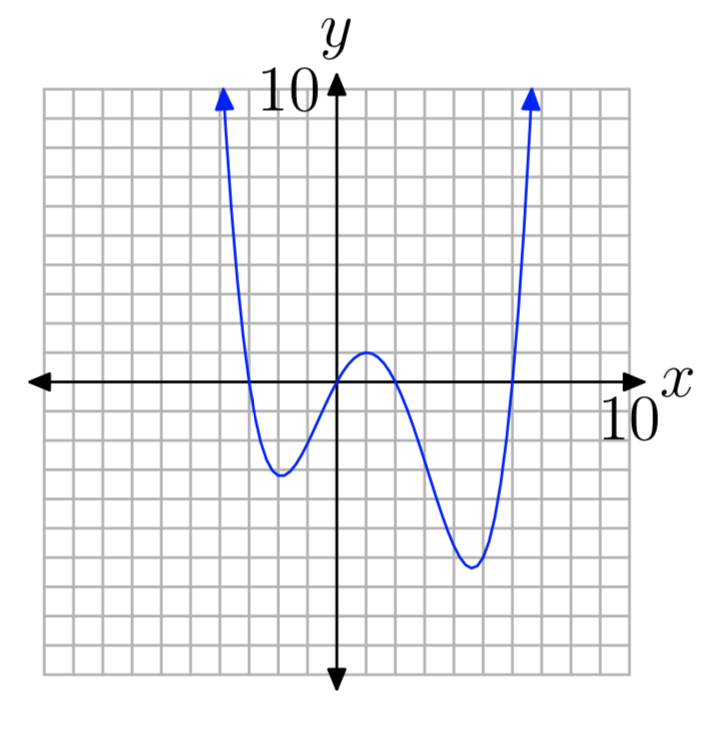
- Responder
-
Ceros: 0, 6, − 3, 2
Ejercicio\(\PageIndex{34}\)
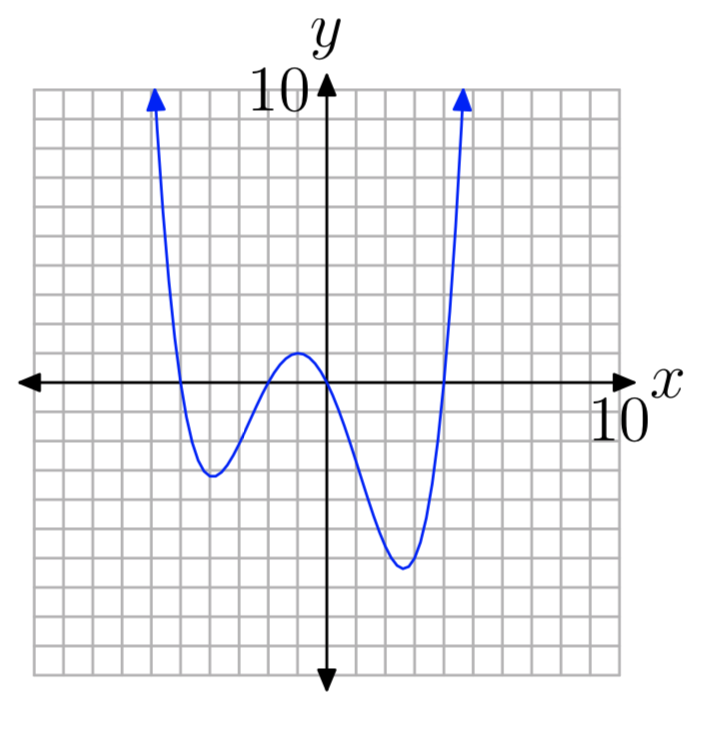
Para cada uno de los polinomios en los Ejercicios 35 - 46, realizar cada una de las siguientes tareas.
- Factorizar el polinomio para obtener los ceros. Muestre su trabajo.
- Configure un sistema de coordenadas en papel gráfico. Etiquetar y escalar el eje horizontal. Utilice los ceros y el comportamiento final para ayudar a bosquejar la gráfica del polinomio sin el uso de una calculadora.
- Verifica tu resultado con una calculadora gráfica.
Ejercicio\(\PageIndex{35}\)
\(p(x) = 5x^3+x^2−45x−9\)
- Responder
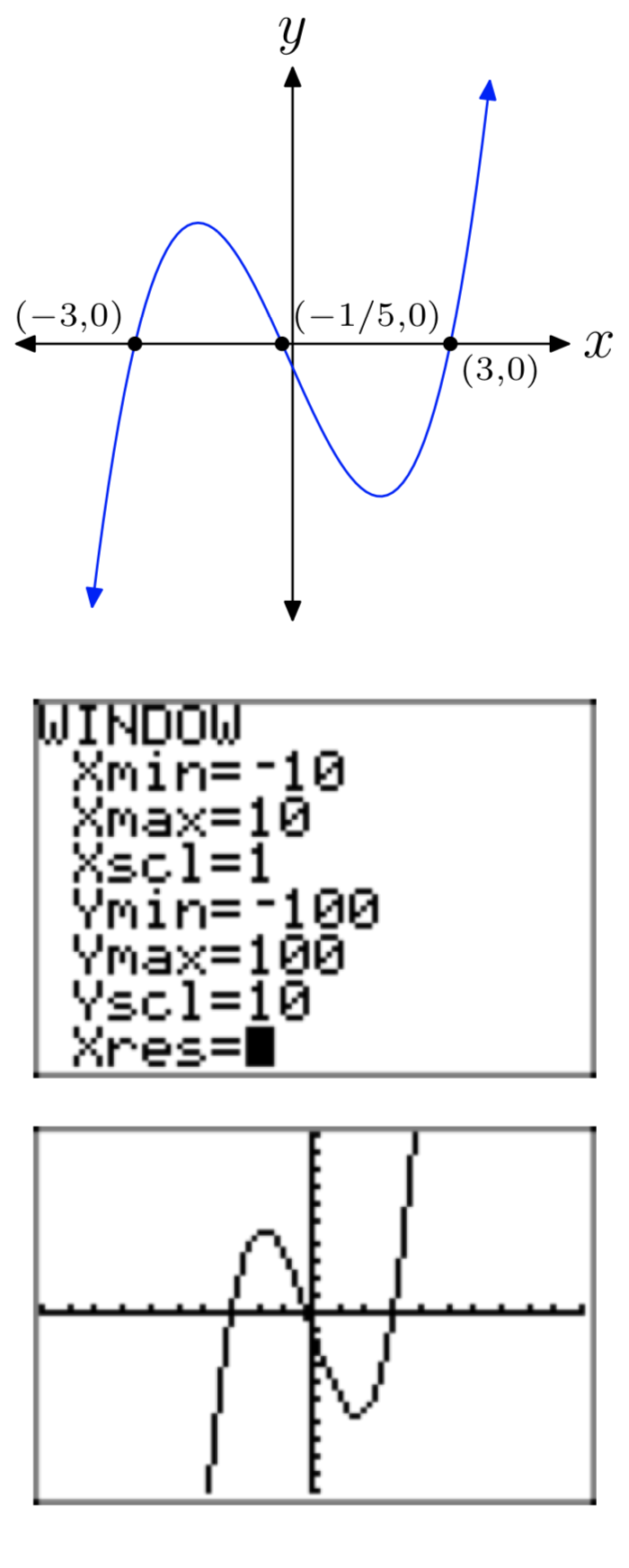
Ejercicio\(\PageIndex{36}\)
\(p(x) = 4x^3+3x^2−64x−48\)
Ejercicio\(\PageIndex{37}\)
\(p(x) = 4x^3−12x^2−9x+27\)
- Responder
-
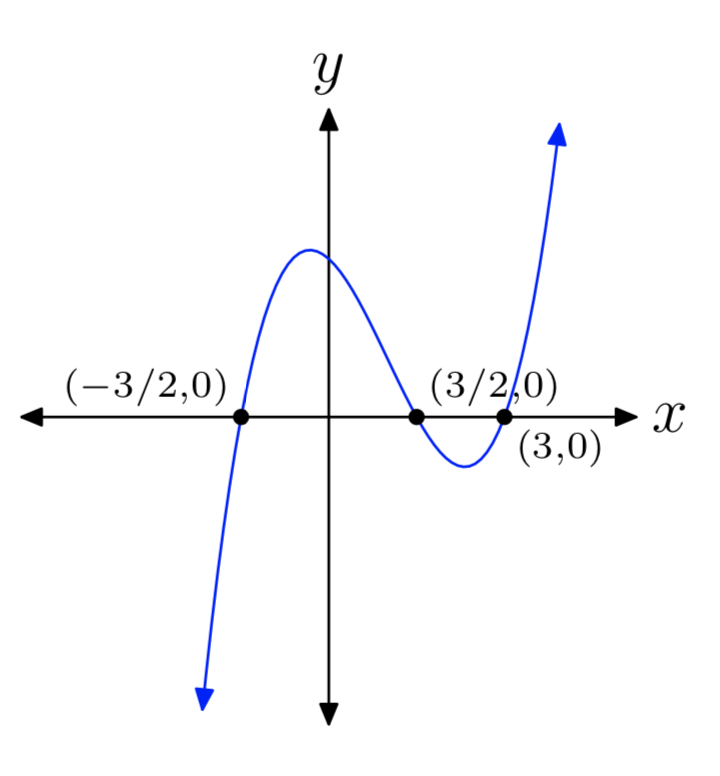
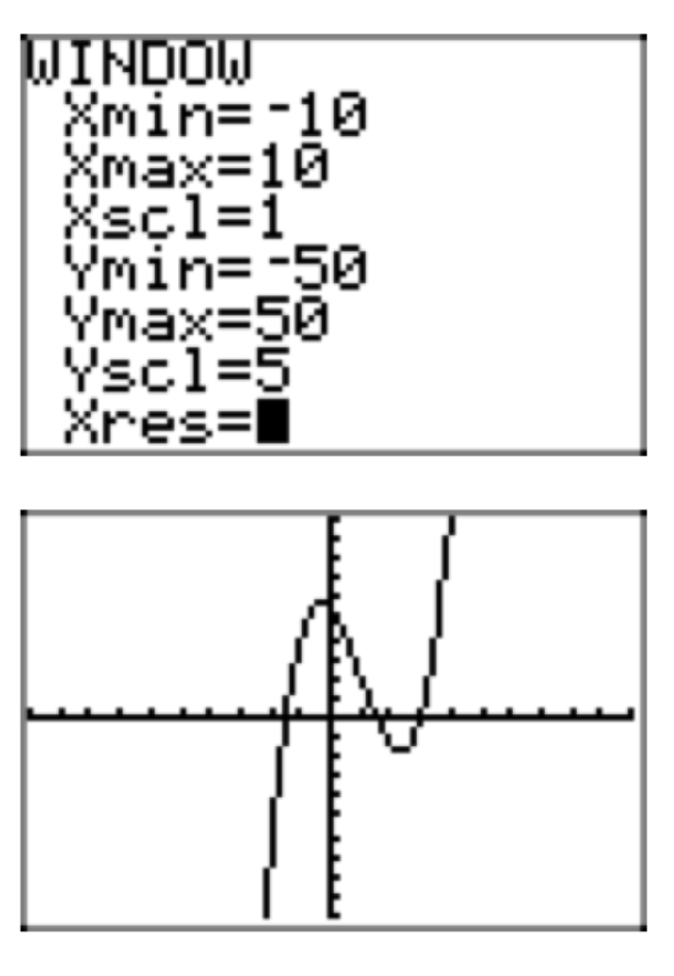
Ejercicio\(\PageIndex{38}\)
\(p(x) = x^3+x^2−16x−16\)
Ejercicio\(\PageIndex{39}\)
\(p(x) = x^4+2x^3−25x^2−50x\)
- Responder
-
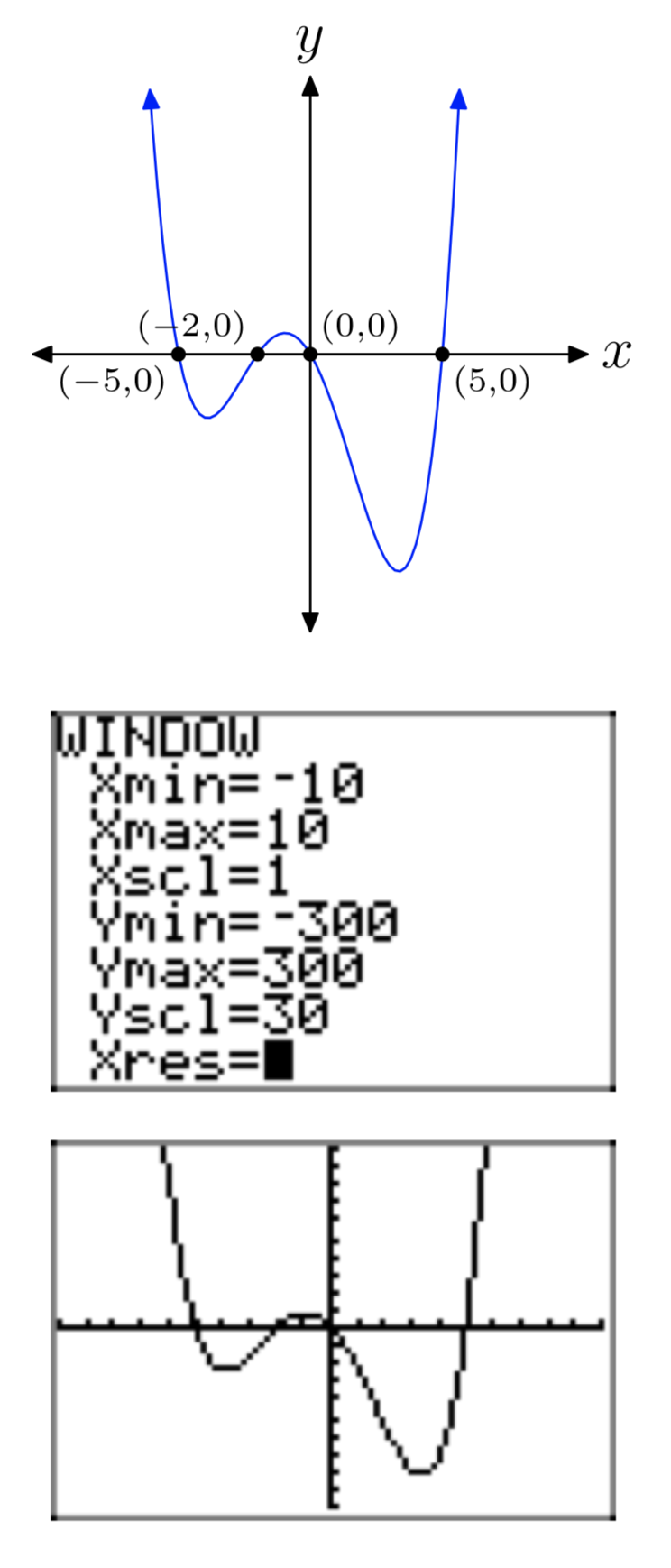
Ejercicio\(\PageIndex{40}\)
\(p(x) = −x^4−5x^3+4x^2+20x\)
Ejercicio\(\PageIndex{41}\)
\(p(x) = −3x^4−9x^3+3x^2+9x\)
- Responder
-
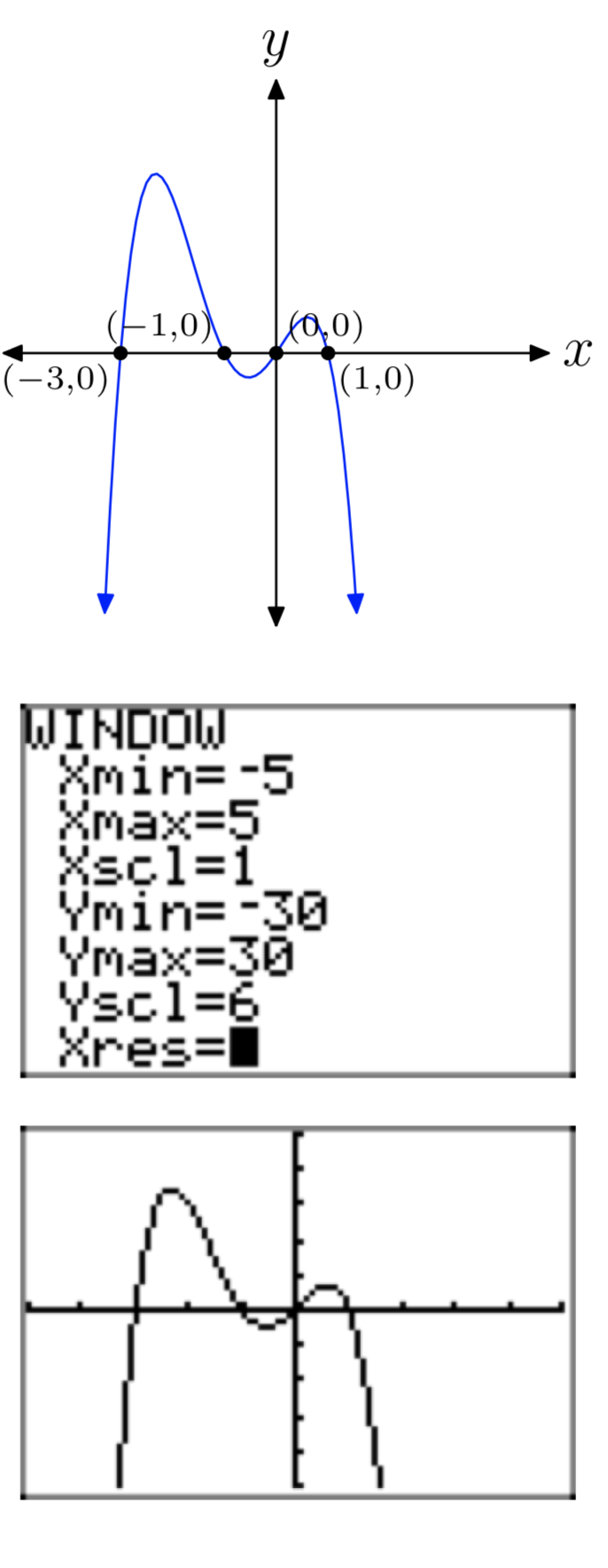
Ejercicio\(\PageIndex{42}\)
\(p(x) = 4x^4−29x^2+25\)
Ejercicio\(\PageIndex{43}\)
\(p(x) = −x^3−x^2+20x\)
- Responder
-
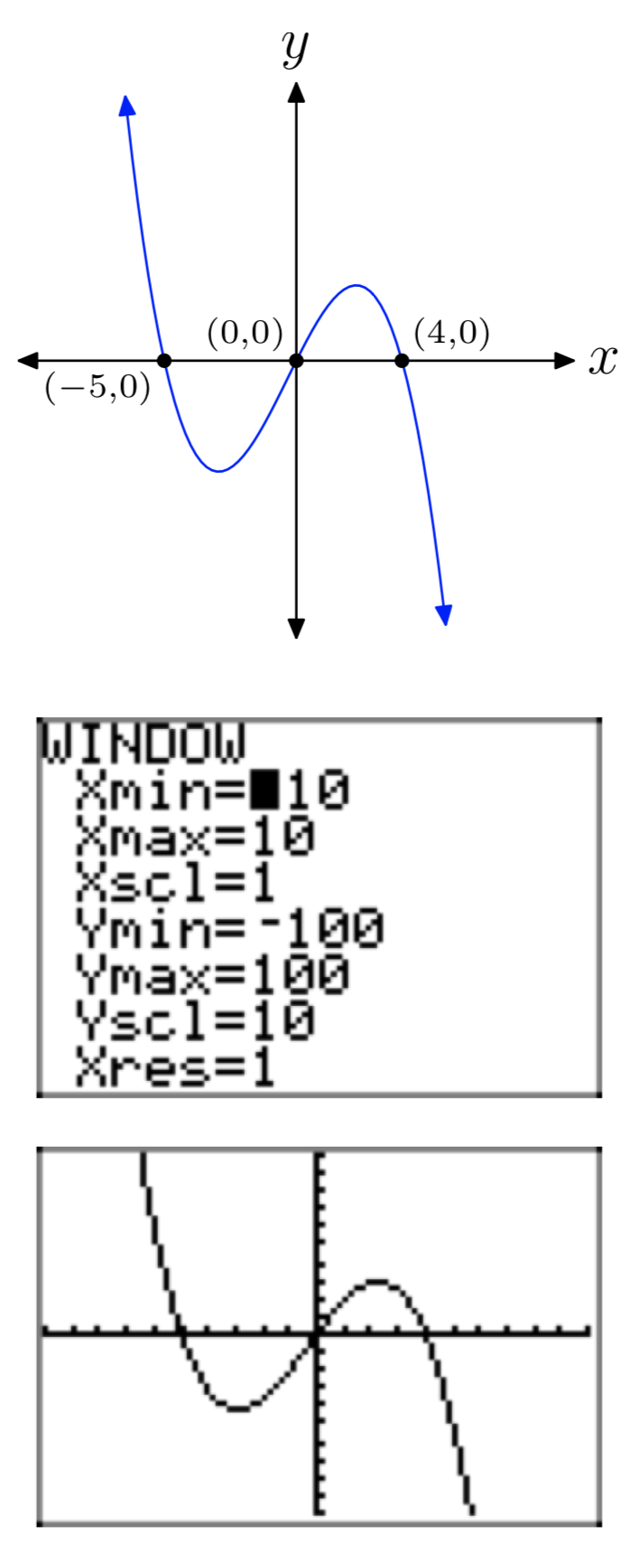
Ejercicio\(\PageIndex{44}\)
\(p(x) = 2x^3−7x^2−30x\)
Ejercicio\(\PageIndex{45}\)
\(p(x) = 2x^3+3x^2−35x\)
- Responder
-
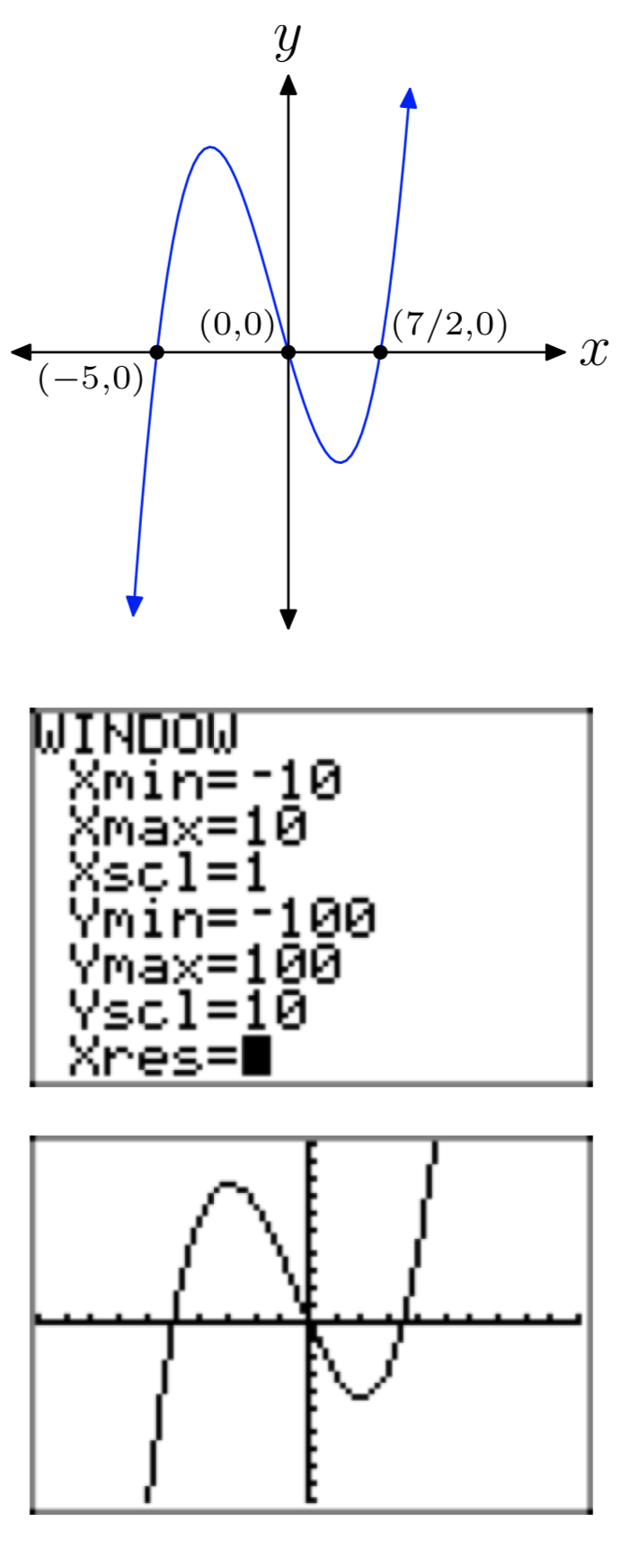
Ejercicio\(\PageIndex{46}\)
\(p(x) = −2x^3−11x^2+21x\)