4.3: Gráfica con Intercepciones

Última actualización
Guardar como PDF

Page ID: 110271

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Al final de esta sección, podrás:

Identificar las intercepciones x e y en una gráfica
Encuentra las intercepciones x e y a partir de una ecuación de una línea
Graficar una línea usando las intercepciones

Nota

Antes de comenzar, toma este cuestionario de preparación.

Resolver:$3\cdot 0+4y=−2$.
Si te perdiste este problema, revisa el Ejercicio 2.2.13.

Identificar las intercepciones x - e y - en una gráfica

Cada ecuación lineal puede ser representada por una línea única que muestra todas las soluciones de la ecuación. Hemos visto que al graficar una línea trazando puntos, se puede utilizar cualquiera de tres soluciones para graficar. Esto significa que dos personas que grafican la línea podrían usar diferentes conjuntos de tres puntos.

A primera vista, sus dos líneas podrían no parecer iguales, ya que tendrían diferentes puntos etiquetados. Pero si todo el trabajo se realizó correctamente, las líneas deberían ser exactamente las mismas. Una forma de reconocer que efectivamente son la misma línea es mirar dónde la línea cruza el eje x y el eje y. A estos puntos se les llama las intercepciones de la línea.

INTERCEPCIONES DE UNA LÍNEA

Los puntos donde una línea cruza el eje x y el eje y se denominan intercepciones de una línea.

Veamos las gráficas de las líneas en la Figura$\PageIndex{1}$.

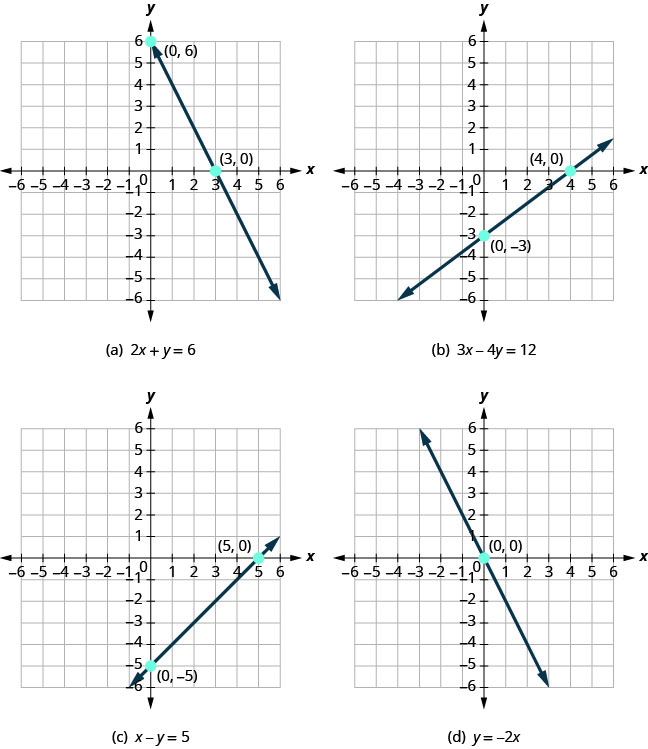
Cuatro figuras, cada una mostrando una línea recta diferente en el plano de coordenadas x y. El eje x de los planos va del 7 al 7 negativo. El eje y de los planos va del negativo 7 al 7. La figura a muestra una línea recta cruzando el eje x en el punto (3, 0) y cruzando el eje y en el punto (0, 6). La gráfica está etiquetada con la ecuación 2x más y es igual a 6. La figura b muestra una línea recta cruzando el eje x en el punto (4, 0) y cruzando el eje y en el punto (0, negativo 3). La gráfica está etiquetada con la ecuación 3x menos 4y es igual a 12. La figura c muestra una línea recta cruzando el eje x en el punto (5, 0) y cruzando el eje y en el punto (0, negativo 5). La gráfica se etiqueta con la ecuación x menos y es igual a 5. La figura d muestra una línea recta que cruza el eje x y el eje y en el punto (0, 0). La gráfica se etiqueta con la ecuación y es igual a negativo 2x. — Figura$\PageIndex{1}$: Ejemplos de gráficas que cruzan el eje x-negativo.

Primero, observe dónde cada una de estas líneas cruza el eje x negativo. Ver Figura$\PageIndex{1}$.

Mesa$\PageIndex{1}$
Figura	La línea cruza el eje x en:	Par ordenado de este punto
Figura (a)	3	(3,0)
Figura (b)	4	(4,0)
Figura (c)	5	(5,0)
Figura (d)	0	(0,0)

¿Ves un patrón?

Para cada fila, la coordenada y del punto donde la línea cruza el eje x es cero. El punto donde la línea cruza el eje x tiene la forma (a,0) y se denomina la intercepción x de una línea. La intercepción x ocurre cuando y es cero. Ahora, veamos los puntos donde estas líneas cruzan el eje y -. Ver Tabla$\PageIndex{2}$.

Mesa$\PageIndex{2}$
Figura	La línea cruza el eje x en:	Par ordenado de este punto
Figura (a)	6	(0,6)
Figura (b)	−3	(0, −3)
Figura (c)	−5	(0,5)
Figura (d)	0	(0,0)

¿Cuál es el patrón aquí?

En cada fila, la coordenada x del punto donde la línea cruza el eje y es cero. El punto donde la línea cruza el eje y tiene la forma (0, b) y se denomina la intercepción y de la línea. La intercepción y ocurre cuando x es cero.

X- INTERCEPCIÓN E Y- INTERCEPCIÓN DE UNA LÍNEA

La intercepción x es el punto (a,0) donde la línea cruza el eje x.

La intercepción y es el punto (0, b) donde la línea cruza el eje y.

Ejercicio$\PageIndex{1}$

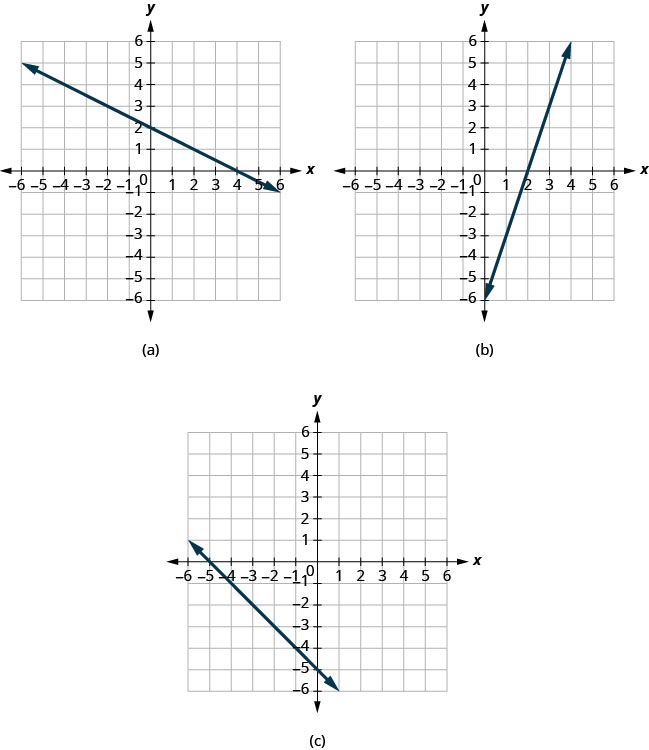
Encuentra las intercepciones x e y en cada gráfica.

Tres figuras, cada una mostrando una línea recta diferente en el plano de coordenadas x y. El eje x de los planos va del 7 al 7 negativo. El eje y de los planos va del negativo 7 al 7. La figura a muestra una línea recta que atraviesa los puntos (negativo 6, 5), (negativo 4, 4), (negativo 2, 3), (0, 2), (2, 1), (4, 0), y (6, negativo 1). La figura b muestra una línea recta que atraviesa los puntos (0, negativo 6), (1, negativo 3), (2, 0), (3, 3) y (4, 6). La figura c muestra una línea recta que atraviesa los puntos (negativo 6, 1), (negativo 5, 0), (negativo 4, negativo 1), (negativo 3, negativo 2), (negativo 2, negativo 3), (negativo 1, negativo 4), (0, negativo 5) y (1, negativo 6). — Figura$\PageIndex{3}$

Contestar: (a) La gráfica cruza el eje x en el punto (4,0). La intercepción x es (4,0).
La gráfica cruza el eje y en el punto (0,2). La intercepción y es (0,2).

b) La gráfica cruza el eje x en el punto (2,0). La intercepción x es (2,0)
La gráfica cruza el eje y en el punto (0, −6). La intercepción y es (0, −6).

(c) La gráfica cruza el eje x en el punto (−5,0). La intercepción x es (−5,0).
La gráfica cruza el eje y en el punto (0, −5). La intercepción y es (0, −5).

Ejercicio$\PageIndex{2}$

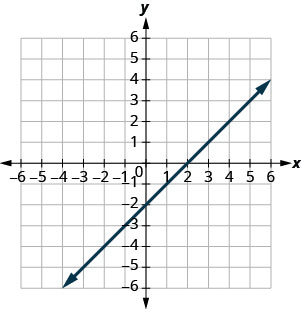
Encuentra las intercepciones x e y en la gráfica.

$Figura que muestra una línea recta en el plano de coordenadas x y. El eje x del plano va de negativo 10 a 10. El eje y de los planos va de negativo 10 a 10. La recta pasa por los puntos (negativo 8, negativo 10), (negativo 6, negativo 8), (negativo 4, negativo 6), (negativo 2, negativo 4), (0, negativo 2), (2, 0), (4, 2), (6, 4), (8, 6) y (10, 8).$

Contestar: x - intercepción: (2,0); y - intercepción: (0, −2)

Ejercicio$\PageIndex{3}$

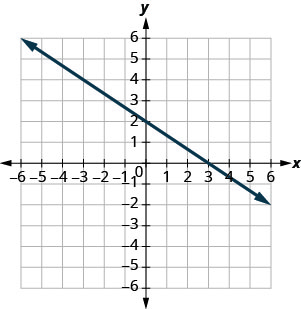
Encuentra las intercepciones x e y en la gráfica.

$La figura muestra una línea recta en el plano de coordenadas x y-. El eje x del plano va de negativo 10 a 10. El eje y de los planos va de negativo 10 a 10. La recta pasa por los puntos (negativo 9, 8), (negativo 6, 6), (negativo 3, 4), (0, 2), (3, 0), (6, negativo 2), y (9, negativo 4).$

Contestar: x - intercepción: (3,0), y - intercepción: (0,2)

Encuentra las intercepciones x - e y - a partir de una ecuación de una línea

Al reconocer que la intercepción x ocurre cuando y es cero y que la y - intercepción ocurre cuando x es cero, nos da un método para encontrar las intercepciones de una línea a partir de su ecuación. Para encontrar la x - intercepción, deje y=0 y resuelva para x. Para encontrar la intercepción y, deje x=0 y resuelva para y.

X- E Y - INTERCEPCIONES DE LA EQUACIÓN DE UNA LÍNEA

Usa la ecuación de la línea. Para encontrar:

la x - intercepción de la línea, dejar y=0 y resolver para x.
la y - intercepción de la línea, dejar x=0 y resolver para y.

Ejercicio$\PageIndex{4}$

Encuentra las intercepciones de 2x+y=6.

Contestar

Vamos a dejar y=0 para encontrar la x - interceptar, y dejar x=0 para encontrar la y - interceptar. Llenaremos la tabla, lo que nos recuerda lo que necesitamos encontrar.

$La figura muestra una tabla con cuatro filas y dos columnas. La primera fila es una fila de título y etiqueta la tabla con la ecuación 2 x más y es igual a 6. La segunda fila es una fila de encabezado y etiqueta cada columna. El encabezado de la primera columna es “x” y el segundo es “y”. La tercera fila está etiquetada como “intercepción x” y tiene la primera columna en blanco y un 0 en la segunda columna. La cuarta fila está etiquetada como “y- interceptar” y tiene un 0 en la primera columna con la segunda columna en blanco.$

Para encontrar la intercepción x, vamos y=0.

Mesa$\PageIndex{3}$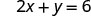
	$.$
Dejar y = 0.	$.$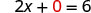
Simplificar.	$.$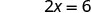
	$.$
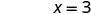
La intercepción x es	(3, 0)
Para encontrar la intercepción y, vamos x = 0.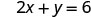
	$.$
Dejar x = 0.	$.$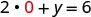
Simplificar.	$.$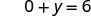
	$.$
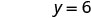
La intercepción y es	(0, 6)

Las intercepciones son los puntos (3,0) y (0,6) como se muestra en la Tabla$\PageIndex{4}$.

Mesa$\PageIndex{4}$
2x+y=6
x	y
3	0
0	6

Ejercicio$\PageIndex{5}$

Encuentra las intercepciones de 3x+y=12.

Contestar: x - intercepción: (4,0), y - intercepción: (0,12)

Ejercicio$\PageIndex{6}$

Encuentra las intercepciones de x+4y=8.

Contestar: x - intercepción: (8,0), y - intercepción: (0,2)

Ejercicio$\PageIndex{7}$

Encuentra las intercepciones de 4x—3y=12.

Contestar

Para encontrar la intercepción x, vamos y = 0.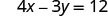
	$.$
Dejar y = 0.	$.$
Simplificar.	$.$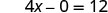
	$.$
	$.$
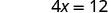
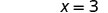
La intercepción x es	(3, 0)
Para encontrar la intercepción y, vamos x = 0.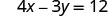
	$.$
Dejar x = 0.	$.$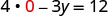
Simplificar.	$.$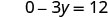
	$.$
	$.$
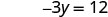
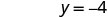
La intercepción y es	(0, −4)

Mesa$\PageIndex{5}$

Las intercepciones son los puntos (3, 0) y (0, −4) como se muestra en la siguiente tabla.

Mesa$\PageIndex{6}$
4x−3y=12
x	y
3	0
0	−4

Ejercicio$\PageIndex{8}$

Encuentra las intercepciones de 3x—4y=12.

Contestar: x - intercepción: (4,0), y - intercepción: (0, −3)

Ejercicio$\PageIndex{9}$

Encuentra las intercepciones de 2x—4y=8.

Contestar: x - intercepción: (4,0), y - intercepción: (0, −2)

Graficar una línea usando las intercepciones

Para graficar una ecuación lineal trazando puntos, es necesario encontrar tres puntos cuyas coordenadas sean soluciones a la ecuación. Puedes usar las intercepciones x - e y - como dos de tus tres puntos. Encuentra las intercepciones y luego encuentra un tercer punto para garantizar la precisión. Asegúrese de que los puntos se alineen hacia arriba y luego dibuje la línea. Este método suele ser la forma más rápida de graficar una línea.

Ejercicio$\PageIndex{10}$: How to Graph a Line Using Intercepts

Gráfica —x+2y=6 usando las intercepciones.

Contestar: $La figura muestra una tabla con el procedimiento general para graficar una línea usando las intercepciones junto con un ejemplo específico usando la ecuación negativo x más 2y es igual a 6. El paso 1 del procedimiento general es “Encuentra las intercepciones x e y- de la línea. Deja que y sea igual a 0 y resuelve para x. Deja que x sea igual a 0 y resuelva para y”. El paso 1 para el ejemplo es una serie de declaraciones y ecuaciones: “Encuentra la x- intercepción. Sea y sea igual a 0”, negativo x más 2y es igual a 6, negativo x más 2 (0) es igual a 6 (donde el 0 es rojo), negativo x es igual a 6, x es negativo 6, “La intercepción x es (negativo 6, 0)”, “Encuentra la y- intercepción. Sea x igual a 0”, x negativo más 2y es igual a 6, 0 negativo más 2y es igual a 6 (donde el 0 es rojo), 2y es igual a 6, y es igual a 3, y “La intercepción y es (0, 3)”.$ $El paso 2 del procedimiento general es “Encontrar otra solución a la ecuación”. El paso 2 para el ejemplo es una serie de declaraciones y ecuaciones: “Usaremos x es igual a 2”, “Let x es igual a 2”, negativo x más 2y es igual a 6, negativo 2 más 2y es igual a 6 (donde el primero 2 es rojo), 2y es igual a 8, y es igual a 4, y “Un tercer punto es (2, 4)”. El paso 3 del procedimiento general es “Trazar los tres puntos. 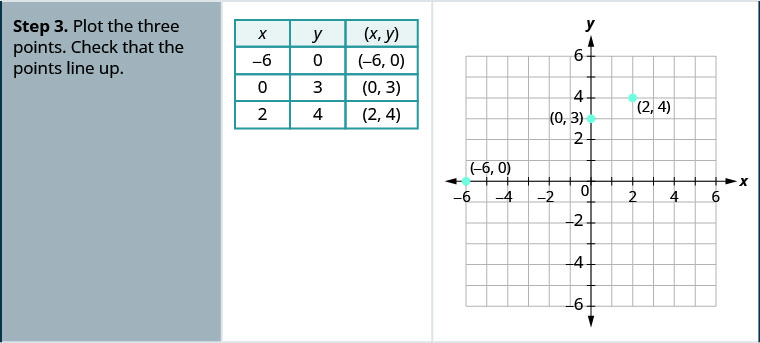Comprueba que los puntos se alineen”.$ $El paso 3 para el ejemplo es una tabla y una gráfica. La tabla tiene cuatro filas y tres columnas. La primera fila es una fila de encabezado y etiqueta cada columna. El encabezado de la primera columna es “x”, el segundo es “y” y el tercero es “(x, y)”. Debajo de la primera columna están los números negativos 6, 0 y 2. Debajo de la segunda columna están los números 0, 3 y 4. Debajo de la tercera columna están los pares ordenados (negativo 6, 0), (0, 3) y (2, 4). La gráfica tiene tres puntos en el plano de coordenadas x- y. El eje x del plano va del negativo 7 al 7. El eje y de los planos va del negativo 7 al 7. 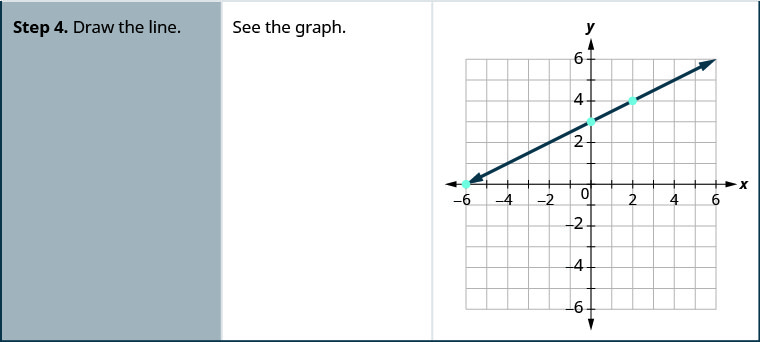Se marcan tres puntos en (negativo 6, 0), (0, 3) y (2, 4).$ $El paso 4 del procedimiento general es “Dibuja la línea”. Para el ejemplo específico, está el enunciado “Ver la gráfica” y una gráfica de una línea recta que pasa por tres puntos en el plano de coordenadas x y-. El eje x del plano va del negativo 7 al 7. El eje y de los planos va del negativo 7 al 7. Se marcan tres puntos en (negativo 6, 0), (0, 3) y (2, 4). La línea recta se dibuja a través de los puntos (negativo 6, 0), (negativo 4, 1), (negativo 2, 2), (0, 3), (2, 4), (4, 5) y (6, 6).$

Ejercicio$\PageIndex{11}$

Gráfica x—2y=4 usando las intercepciones.

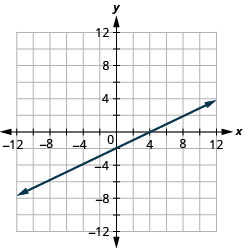
Contestar: $La figura muestra una línea recta en el plano de coordenadas x y-. El eje x del plano va de negativo 12 a 12. El eje y de los planos va de negativo 12 a 12. La recta pasa por los puntos (negativo 10, negativo 7), (negativo 8, negativo 6), (negativo 6, negativo 5), (negativo 4, negativo 4), (negativo 2, negativo 3), (0, negativo 2), (2, negativo 1), (4, 0), (6, 1), (8, 2) y (10, 3).$

Ejercicio$\PageIndex{12}$

Gráfica —x+3y=6 usando las intercepciones.

Contestar: $La figura muestra una línea recta en el plano de coordenadas x y-. El eje x del plano va de negativo 12 a 12. El eje y de los planos va de negativo 12 a 12. La recta pasa por los puntos (negativo 12, negativo 2), (negativo 9, negativo 1), (negativo 6, 0), (negativo 3, 1), (0, 2), (3, 3), (6, 4), (9, 5) y (12, 6).$

Los pasos para graficar una ecuación lineal usando las intercepciones se resumen a continuación.

GRÁFICA UNA Ecuación Lineal usando las Intercepciones

Encuentra las intercepciones x e y de la línea.
- Dejar y=0 y resolver para x
- Deje x=0 y resuelva para y.
Encuentra una tercera solución a la ecuación.
Trazar los tres puntos y verificar que se alineen.
Dibuja la línea.

Ejercicio$\PageIndex{13}$

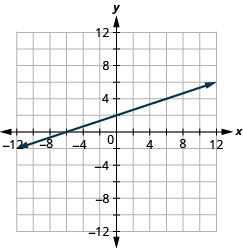
Gráfica 4x—3y=12 usando las intercepciones.

Contestar

Encuentra las intercepciones y un tercer punto.

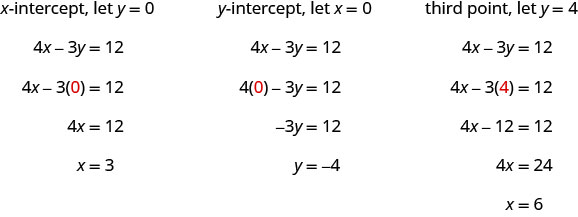
$La figura muestra una serie de afirmaciones y ecuaciones: “Encuentra la x- intercepción. Sea y sea igual a 0”, 4x menos 3y es igual a 12, 4x menos 3 (0) es igual a 12 (donde el 0 es rojo), 4x es igual a 12, x es igual a 3, “Encuentra la intercepción y. Sea x igual a 0”, 4x menos 3y es igual a 12, 4 (0) menos 3y es igual a 12 (donde el 0 es rojo), negativo 3y es igual a 12, y es igual a 4 negativo, “tercer punto, let y es igual a 4”, 4x menos 3y es igual a 12, 4x menos 3 (4) es igual a 12 (donde el segundo 4 es rojo), 4x menos 12 es igual a 12, 4x es igual a 24 y x es igual a 6.$

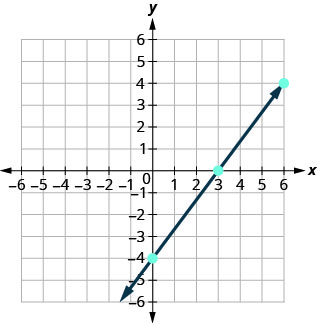
Enlistamos los puntos en Tabla$\PageIndex{7}$ y mostramos la gráfica a continuación.

4x−3y=12
x	y	(x, y)
3	0	(3,0)
0	−4	(0, −4)
6	4	(6,4)

Mesa$\PageIndex{7}$

$En la figura se muestra la gráfica de una línea recta que atraviesa tres puntos en el plano de la coordenada x y. El eje x del plano va del negativo 7 al 7. El eje y de los planos va del negativo 7 al 7. Tres puntos están marcados en (0, negativo 4), (3, 0) y (6, 4). La línea recta se dibuja a través de los puntos (0, negativo 4), (3, 0) y (6, 4).$

Ejercicio$\PageIndex{14}$

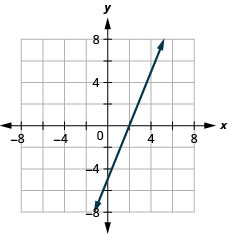
Gráfica 5x—2y=10 usando las intercepciones.

Contestar: $La figura muestra la gráfica de una línea recta en el plano de coordenadas x y. El eje x del plano va del negativo 7 al 7. El eje y de los planos va del negativo 7 al 7. La recta pasa por los puntos (0, negativo 5), (2, 0) y (4, 5).$

Ejercicio$\PageIndex{15}$

Gráfica 3x—4y=12 usando las intercepciones.

Contestar: $La figura muestra la gráfica de una línea recta en el plano de coordenadas x y. El eje x del plano va del negativo 7 al 7. El eje y de los planos va del negativo 7 al 7. La recta pasa por los puntos (negativo 4, negativo 6), (0, negativo 3) y (4, 0).$

Ejercicio$\PageIndex{16}$

Gráfica y=5x usando las intercepciones.

Contestar

$La figura muestra dos conjuntos de declaraciones y ecuaciones para encontrar las intercepciones a partir de una ecuación. El primer conjunto de declaraciones y ecuaciones es “x- interceptar”, “let y es igual a 0”, y es igual a 5x, 0 es igual a 5x (donde el 0 es rojo), 0 es igual a x, (0, 0). El segundo conjunto de sentencias y ecuaciones es “y- interceptar”, “let x es igual a 0”, y es igual a 5x, y es igual a 5 (0) (donde el 0 es rojo), y es igual a 0, (0, 0).$

Esta línea tiene sólo una interceptación. Es el punto (0,0).

Para asegurar la precisión necesitamos trazar tres puntos. Dado que las intercepciones x - e y - son el mismo punto, necesitamos dos puntos más para graficar la línea.

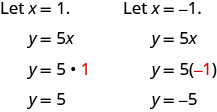
$La figura muestra dos conjuntos de enunciados y ecuaciones para encontrar dos puntos a partir de una ecuación. El primer conjunto de declaraciones y ecuaciones es “Let x es igual a 1”, y es igual a 5x, y es igual a 5 (1) (donde el 1 es rojo), y es igual a 5. El segundo conjunto de declaraciones y ecuaciones es “Let x es igual a negativo 1”, y es igual a 5x, y es igual a 5 (negativo 1) (donde el negativo 1 es rojo), y es igual a negativo 5.$

Ver Tabla$\PageIndex{8}$.

y=5x
x	y	(x, y)
		(0,0)
		(1,5)
−1	−5	(−1, −5)

Mesa$\PageIndex{8}$

Trazar los tres puntos, verificar que se alineen y trazar la línea.

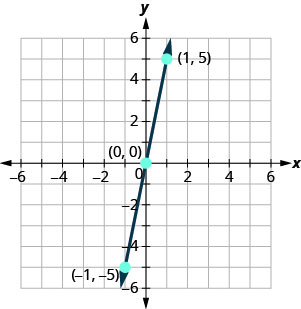
$En la figura se muestra la gráfica de una línea recta que atraviesa tres puntos en el plano de la coordenada x y. El eje x del plano va de negativo 10 a 10. El eje y de los planos va de negativo 10 a 10. Tres puntos están marcados y etiquetados con sus coordenadas en (negativo 1, negativo 5), (0, 0) y (1, 5). La línea recta se dibuja a través de los puntos (negativo 1, negativo 5), (0, 0) y (1, 5).$

Ejercicio$\PageIndex{17}$

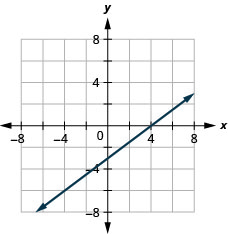
Gráfica y=4x usando las intercepciones.

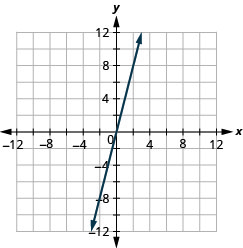
Contestar: $La figura muestra una línea recta en el plano de coordenadas x y-. El eje x del plano va de negativo 12 a 12. El eje y de los planos va de negativo 12 a 12. La recta pasa por los puntos (negativo 4, negativo 12), (negativo 3, negativo 9), (negativo 2, negativo 6), (negativo 1, negativo 3), (0, 0), (1, 3), (2, 6), (3, 9) y (4, 12).$

Ejercicio$\PageIndex{18}$

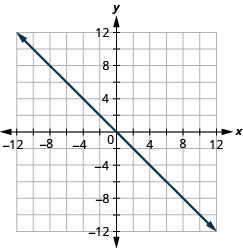
Gráfica y=−x las intercepciones.

Contestar: $La figura muestra una línea recta en el plano de coordenadas x y-. El eje x del plano va de negativo 12 a 12. El eje y de los planos va de negativo 12 a 12. La recta pasa por los puntos (negativo 10, 10), (negativo 9, 9), (negativo 8, 8), (negativo 7, 7), (negativo 6, 6), (negativo 5, 5), (negativo 4, 4), (negativo 3, 3), (negativo 2, 2), (negativo 1, 1), (0, 0), (1, negativo 1), (2, negativo 2), (3, negativo 3), (4, negativo 4), (5, negativo 5), (6) negativo 6), (7, negativo 7), (8, negativo 8), (9, negativo 9) y (10, negativo 10).$

Conceptos clave

Encuentra las intercepciones x - e y - a partir de la ecuación de una línea
- Usa la ecuación de la línea para encontrar la x - intercepción de la línea, deja y=0 y resuelve para x.
- Usa la ecuación de la línea para encontrar la y - intercepción de la línea, deja x=0 y resuelve para y.
Graficar una Ecuación Lineal usando las Intercepciones
1. Encuentra las intercepciones x e y de la línea.
  Deje y=0 y resuelva para x.
  Deje x=0 y resuelva para y.
2. Encuentra una tercera solución a la ecuación.
3. Trazar los tres puntos y luego verificar que se alineen.
4. Dibuja la línea.
Estrategia para elegir el método más conveniente para graficar una línea:
- Considera la forma de la ecuación.
- Si sólo tiene una variable, es una línea vertical u horizontal.
  x=a es una línea vertical que pasa por el eje x - en a
  y=b es una línea horizontal que pasa por el eje y - en b.
- Si y se aísla en un lado de la ecuación, grafica trazando puntos.
- Elija tres valores cualesquiera para x y luego resuelva para los valores y - correspondientes.
- Si la ecuación es de la forma ax+por=c, encuentra las intercepciones. Encuentra las intercepciones x - e y - y luego un tercer punto.

Glosario

intercepciones de una línea: Los puntos donde una línea cruza el eje x y el eje y se denominan las intercepciones de la línea.

x - interceptar: El punto (a,0) donde la línea cruza el eje x -; la intercepción x ocurre cuando y es cero.

y -interceptar: El punto (0, b) donde la línea cruza el eje y; la intercepción y ocurre cuando x es cero.

Search

Text Color

Text Size

Margin Size

Font Type

INTERCEPCIONES DE UNA LÍNEA

X- INTERCEPCIÓN E Y- INTERCEPCIÓN DE UNA LÍNEA

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

X- E Y - INTERCEPCIONES DE LA EQUACIÓN DE UNA LÍNEA

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\): How to Graph a Line Using Intercepts

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

GRÁFICA UNA Ecuación Lineal usando las Intercepciones

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejercicio\(\PageIndex{15}\)

Ejercicio\(\PageIndex{16}\)

Ejercicio\(\PageIndex{17}\)

Ejercicio\(\PageIndex{18}\)