7.2: Reducción de las funciones racionales

El objetivo de esta sección es aprender a reducir una expresión racional a “términos más bajos”. Por supuesto, eso significa que tendremos que entender qué se entiende por la frase “términos más bajos”. Con ese pensamiento en mente, comenzamos con una discusión sobre el mayor divisor común de un par de enteros.

Primero, definimos a qué nos referimos con “divisibilidad”.

Definición

Supongamos que tenemos un par de enteros a y b. decimos que “a es un divisor de b”, o “a divide b” si y sólo si hay otro entero k de manera que b = ak. Otra forma de decir lo mismo es decir que a divide b si, al dividir b por a, el resto es cero.

Veamos un ejemplo.

Ejemplo\(\PageIndex{1}\)

¿Cuáles son los divisores de 12?

Solución

Porque\(12=1 \times 12\), tanto 1 como 12 son divisores de 12. Porque\(12=2 \times 6\), tanto 2 como 6 son divisores de 12. Por último\(12=3 \times 4\), porque, tanto 3 como 4 son divisores de 12. Si los enumeramos en orden ascendente, los divisores de 12 son\[1,2,3,4,6, \text { and } 12\]

Veamos otro ejemplo.

Ejemplo\(\PageIndex{2}\)

¿Cuáles son los divisores de 18?

Solución

Porque\(18=1 \times 18\), tanto 1 como 18 son divisores de 18. De igual manera\(18=3 \times 6\),\(18=2 \times 9\) y, así en orden ascendente, los divisores de 18 son

\[1,2,3,6,9, \text { and } 18\]

El divisor más común de dos o más enteros es el divisor más grande que comparten los enteros en común. Un ejemplo debería dejar esto claro.

Ejemplo\(\PageIndex{3}\)

¿Cuál es el mayor divisor común de 12 y 18?

Solución

En el Ejemplo 2 y en el Ejemplo 3, vimos lo siguiente.

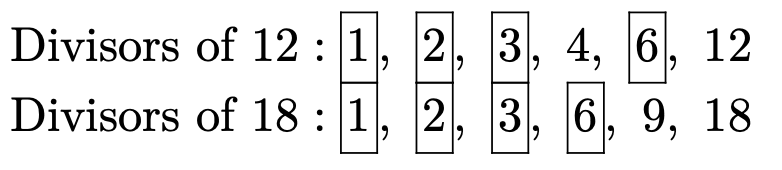
Hemos enmarcado los divisores que 12 y 18 tienen en común. Son 1, 2, 3 y 6. El “mayor” de estos divisores “comunes” es 6. De ahí que digamos que “el mayor divisor común de 12 y 18 es el 6”.

Definición

El divisor más común de dos enteros a y b es el divisor más grande que tienen en común. Utilizaremos la notación\[GCD(a, b)\] para representar el mayor divisor común de a y b.

Así, como vimos en el Ejemplo 4, GCD (12, 18) = 6.

Cuando el mayor divisor común de un par de enteros es uno, le damos un nombre especial a ese par.

Definición

Que a y b sean números enteros. Si el divisor más común de a y b es uno, es decir, si GCD (a, b) = 1, entonces decimos que a y b son relativamente primos.

Por ejemplo:

• 9 y 12 no son relativamente primos porque GCD (9, 12) = 3.
• 10 y 15 no son relativamente primos porque GCD (10, 15) = 5.
• 8 y 21 son relativamente primos porque GCD (8, 21) = 1.

Ahora podemos definir qué se entiende cuando decimos que un número racional se reduce a los términos más bajos.

Definición

Se dice que un número racional en la forma p/q, donde p y q son números enteros, se reduce a términos más bajos si y sólo si GCD (p, q) = 1. Es decir, p/q se reduce a términos más bajos si el divisor más común tanto del numerador como del denominador es 1.

Como vimos en Ejemplo\(\PageIndex{3}\), el mayor divisor común de 12 y 18 es 6. Por lo tanto, la fracción 12/18 no se reduce a los términos más bajos. Sin embargo, podemos reducir 12/18 a términos más bajos dividiendo tanto el numerador como el denominador por su divisor más común. Es decir,

\[\frac{12}{18}=\frac{12 \div 6}{18 \div 6}=\frac{2}{3}\]

Tenga en cuenta que GCD (2, 3) = 1, por lo que 2/3 se reduce a los términos más bajos.

Cuando sea difícil determinar el divisor más común, nos resultará más eficiente proceder de la siguiente manera:

• Factor primo tanto numerador como denominador.

• Cancelar factores comunes.

Así, para reducir 12/18 a términos más bajos, primero expresar tanto el numerador como el denominador como producto de números primos, luego cancelar los primos comunes.

\[\frac{12}{18}=\frac{2 \cdot 2 \cdot 3}{2 \cdot 3 \cdot 3}=\frac{\not{2} \cdot 2 \cdot \not{3}}{\not{2} \cdot 3 \cdot \not{3}}=\frac{2}{3}\]

Cuando cancelas un 2, en realidad estás dividiendo tanto el numerador como el denominador por 2. Cuando cancelas un 3, en realidad estás dividiendo tanto el numerador como el denominador por 3. Tenga en cuenta que hacer ambas (dividiendo por 2 y luego dividiendo por 3) equivale a dividir tanto el numerador como el denominador por 6.

Vamos a favorecer esta última técnica, precisamente porque es idéntica a la técnica que usaremos para reducir las funciones racionales a los términos más bajos. Sin embargo, esta técnica de “cancelación” tiene algunas trampas, así que tomemos un momento para discutir algunos errores comunes de cancelación.

Cancelación

Puede provocar un debate bastante acalorado entre los educadores de matemáticas al mencionar inocentemente la palabra “cancelación”. Parece haber dos campamentos diametralmente opuestos, los que no les importa cuando sus alumnos utilizan la técnica de cancelación, y por otro lado, los que se niegan incluso a usar el término “cancelación” en sus clases.

Ambos lados del argumento tienen mérito. Como mostramos en la ecuación (8), podemos reducir 12/18 de manera bastante eficiente simplemente cancelando factores comunes. Por otro lado, los instructores del segundo campamento prefieren usar la frase “factorizar un 1” en lugar de la frase “cancelar”, alentando a sus alumnos a reducir 12/18 de la siguiente manera.

\[\frac{12}{18}=\frac{2 \cdot 2 \cdot 3}{2 \cdot 3 \cdot 3}=\frac{2}{3} \cdot \color{blue}{\frac{2 \cdot 3}{2 \cdot 3}}=\frac{2}{3} \cdot 1=\frac{2}{3}\]

Esta es una técnica perfectamente válida y que, honestamente, evita las arenas movedizas de los “errores de cancelación”. Los instructores que se cansan de ver a sus alumnos “cancelar” cuando no deberían es muy probable que promuevan esta última técnica.

Sin embargo, si podemos ayudar a nuestros alumnos a evitar “errores de cancelación”, preferimos permitir que nuestros alumnos cancelen factores comunes (como hicimos en la ecuación (8)) al reducir fracciones como 12/18 a términos más bajos. Entonces, con estos pensamientos en mente, discutamos algunos de los errores de cancelación más comunes.

Comencemos con un consejo de lo más importante.

Cómo evitar errores de cancelación

Solo puedes cancelar factores, no adiciones. Para evitar errores de cancelación, factorizar completamente antes de comenzar a cancelar.

Advertencia

Muchos de los cálculos subsiguientes son incorrectos. Son ejemplos de errores comunes que se cometen al realizar la cancelación. Asegúrate de leer atentamente y evita simplemente “escanear” estos cálculos.

Como primer ejemplo, considere la expresión racional

\[\frac{2+6}{2}\]

que claramente equivale a 8/2, o 4. No obstante, si cancela en esta situación, como en

\[\frac{2+6}{2}=\frac{\not{2}+6}{\not{2}}\]

desde luego no obtienes el mismo resultado. Entonces, ¿qué pasó?

Obsérvese que en el numerador de la ecuación (10), el 2 y el 6 están separados por un signo más. Así, no son factores; ¡son adiciones! No se le permite cancelar adendas, solo factores.

Supongamos, a modo de comparación, que la expresión racional había sido

\[\frac{2 \cdot 6}{2}\]

que claramente equivale a 12/2, o 6. En este caso, el 2 y el 6 en el numerador están separados por un símbolo de multiplicación, por lo que son factores y se permite la cancelación, como en

\[\frac{2 \cdot 6}{2}=\frac{\not{2} \cdot 6}{\not{2}}=6\]

Ahora bien, antes de descartar estos ejemplos como triviales, considere los siguientes ejemplos que son idénticos en estructura. Primero, considere

\[\frac{x+(x+2)}{x}=\frac{\not{x}+(x+2)}{\not{x}}=x+2\]

Esta cancelación es idéntica a la realizada en la ecuación (10) y no está permitida. En el numerador, tenga en cuenta que x y (x+2) están separados por un símbolo de suma, por lo que son adiciones. ¡No se le permite cancelar adendas!

Por el contrario, considere el siguiente ejemplo.

\[\frac{x(x+2)}{x}=\frac{\not{x}(x+2)}{\not{x}}=x+2\]

En el numerador de este ejemplo, x y (x+2) están separados por multiplicación implícita. De ahí que sean factores y la cancelación es permisible.

Vuelva a mirar la ecuación (10), donde la respuesta correcta debería haber sido 8/2, o 4. Nos pareció erróneamente que la respuesta era 6, porque cancelamos las adiciones. Una solución alternativa sería factorizar primero el numerador de la ecuación (10), luego cancelar, de la siguiente manera.

\[\frac{2+6}{2}=\frac{2(1+3)}{2}=\frac{\not{2}(1+3)}{\not{2}}=1+3=4\]

Tenga en cuenta que cancelamos factores en este enfoque, que es permisible, y obtuvimos la respuesta correcta 4.

Advertencia

Hemos terminado de discutir errores comunes de cancelación y es posible que no sigas leyendo con confianza que todas las matemáticas se presentan correctamente.

Reducción de expresiones racionales en x

Ahora que hemos discutido algunas ideas y técnicas fundamentales, apliquemos lo que hemos aprendido a expresiones racionales que son funciones de una variable independiente (generalmente x). Empecemos con un ejemplo sencillo.

Ejemplo\(\PageIndex{4}\)

Reducir la expresión racional\[\frac{2 x-6}{x^{2}-7 x+12}\] a los términos más bajos. ¿Para qué valores de x es válido tu resultado?

Solución

En el numerador, factorial un 2, como en 2x − 6 = 2 (x − 3).

El denominador es un trinomio cuadrático con ac = (1) (12) = 12. El par entero −3 y −4 tiene el producto 12 y la suma −7, por lo que el denominador factores como se muestra.

\[\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(x-3)}{(x-3)(x-4)}\]

Ahora que se factorizan tanto el numerador como el denominador, podemos cancelar factores comunes.

\[\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(x-3)}{(x-3)(x-4)}=\frac{2}{x-4}\]

Así, hemos demostrado que\[\frac{2 x-6}{x^{2}-7 x+12}=\frac{2}{x-4}\]

En la ecuación (15), estamos afirmando que la expresión de la izquierda (la expresión original) es idéntica a la expresión de la derecha para todos los valores de x.

En realidad, hay dos excepciones notables, la primera de las cuales es x = 3. Si sustituimos x = 3 en el lado izquierdo de la ecuación (15), obtenemos

\[\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(3)-6}{(3)^{2}-7(3)+12}=\frac{0}{0}\]

No podemos dividir por cero, por lo que el lado izquierdo de la ecuación (15) no está definido si x = 3. Por lo tanto, el resultado en la ecuación (15) no es válido si x = 3.

Del mismo modo, si insertamos x = 4 en el lado izquierdo de la ecuación (15),

\[\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(4)-6}{(4)^{2}-7(4)+12}=\frac{2}{0}\]

Nuevamente, la división por cero es indefinida. El lado izquierdo de la ecuación (15) no está definido si x = 4, por lo que el resultado en la ecuación (15) no es válido si x = 4. Tenga en cuenta que el lado derecho de la ecuación (15) también está indefinido en x = 4.

Sin embargo, el trabajo algebraico que hicimos anteriormente garantiza que el lado izquierdo de la ecuación (15) será idéntico al lado derecho de la ecuación (15) para todos los demás valores de x Por ejemplo, si sustituimos x = 5 en el lado izquierdo de la ecuación (15),

\[\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(5)-6}{(5)^{2}-7(5)+12}=\frac{4}{2}=2\]

Por otro lado, si sustituimos x = 5 en el lado derecho de la ecuación (15),

\[\frac{2}{x-4}=\frac{2}{5-4}=2\]

De ahí que ambos lados de la ecuación (15) sean idénticos cuando x = 5. De manera similar, podríamos verificar la validez de la identidad en la ecuación (15) para todos los demás valores de x

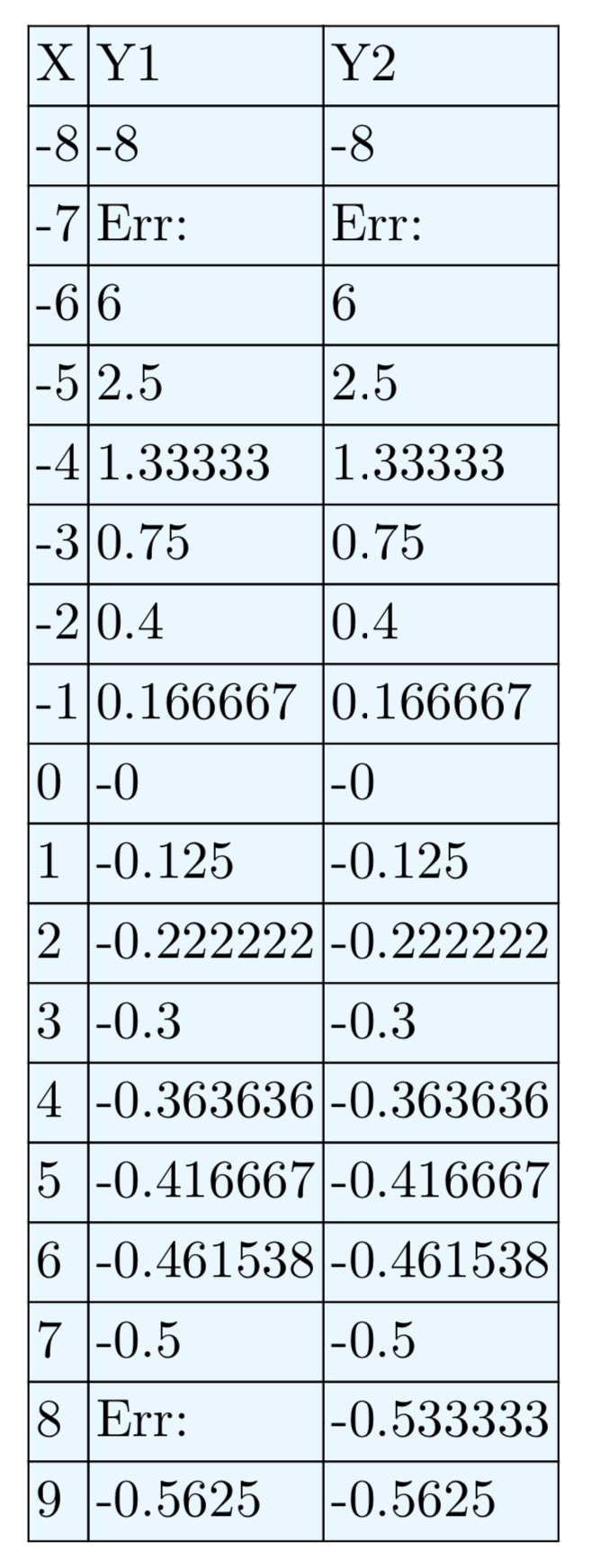
Puede utilizar la calculadora gráfica para verificar la identidad en la ecuación (15). Cargue los lados izquierdo y derecho de la ecuación (15) en el menú Y=, como se muestra en la Figura\(\PageIndex{1}\) (a). Presione 2nd TBLSET y ajuste los ajustes como se muestra en la Figura\(\PageIndex{1}\) (b). Asegúrese de resaltar AUTO tanto para variables independientes como dependientes y presione ENTRAR en cada una para que la selección sea permanente. En la Figura\(\PageIndex{1}\) (b), tenga en cuenta que hemos establecido tblStart = 0 y ∆Tbl = 1. Presione 2da TABLA para producir los resultados tabulares mostrados en la Figura\(\PageIndex{1}\) (c).

Figura\(\PageIndex{1}\). Usando la calculadora gráfica para verificar que los lados izquierdo y derecho de la ecuación (15) son idénticos.

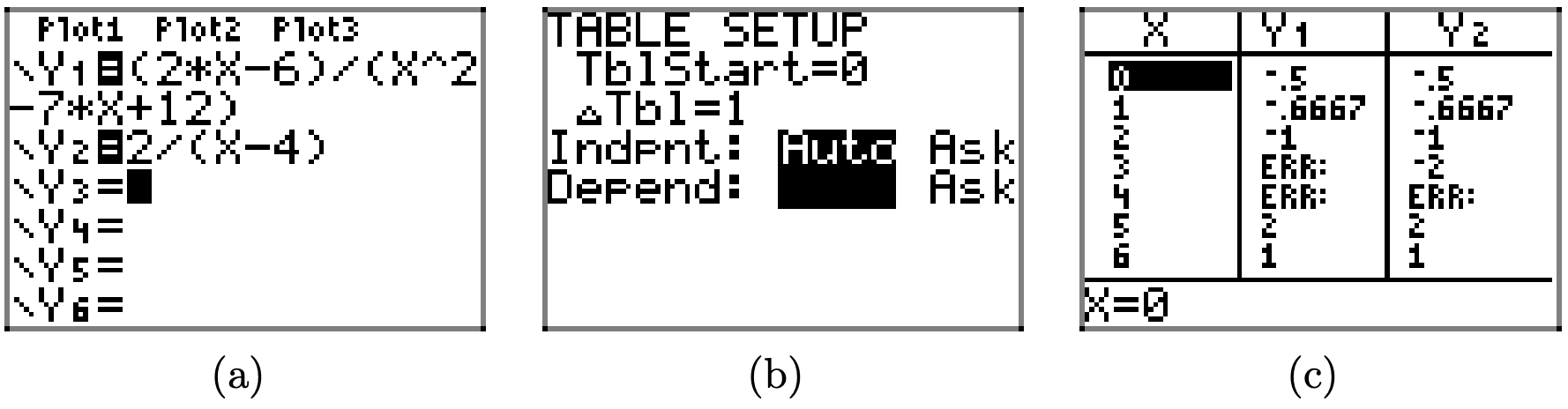
Recuerde que colocamos los lados izquierdo y derecho de la ecuación (15) en Y1 e Y2, respectivamente.

• En los resultados tabulares de la Figura\(\PageIndex{1}\) (c), anote el mensaje ERR (error) en Y1 cuando x = 3 y x = 4. Esto concuerda con nuestros hallazgos anteriores, donde el lado izquierdo de la ecuación (15) estaba indefinido debido a la presencia de cero en el denominador cuando x = 3 o x = 4.
• En los resultados tabulares de la Figura\(\PageIndex{1}\) (c), nótese que el valor de Y1 e Y2 concuerda para todos los demás valores de x.

Nos llevan al siguiente resultado clave.

Restricciones

En general, cuando se reduce una expresión racional a términos más bajos, la expresión obtenida debe ser idéntica a la expresión original para todos los valores de las variables en cada expresión, guardar aquellos valores de las variables que hacen que cualquier denominador sea igual a cero. Esto se aplica al denominador en la expresión original, a todas las expresiones intermedias de tu obra, y al resultado final. Nos referiremos a cualquier valor de la variable que haga que cualquier denominador sea igual a cero como restricciones.

Veamos otro ejemplo.

Ejemplo\(\PageIndex{5}\)

Reducir la expresión\[\frac{2 x^{2}+5 x-12}{4 x^{3}+16 x^{2}-9 x-36}\] a los términos más bajos. Estado todas las restricciones.

Solución

El numerador es un trinomio cuadrático con ac = (2) (−12) = −24. El par entero −3 y 8 tienen producto −24 y suma 5. Romper el término medio del polinomio en el numerador en una suma usando este par entero, luego factorizar por agrupación.

\[\begin{aligned} 2 x^{2}+5 x-12 &=2 x^{2}-3 x+8 x-12 \\ &=x(2 x-3)+4(2 x-3) \\ &=(x+4)(2 x-3) \end{aligned}\]

Factorizar el denominador por agrupación.

\[\begin{aligned} 4 x^{3}+16 x^{2}-9 x-36 &=4 x^{2}(x+4)-9(x+4) \\ &=\left(4 x^{2}-9\right)(x+4) \\ &=(2 x+3)(2 x-3)(x+4) \end{aligned}\]

Observe cómo se utilizó la diferencia de patrón de dos cuadrados para factorizar\(4x^2 − 9 = (2x + 3)(2x − 3)\) en el último paso.

Ahora que hemos factorizado tanto el numerador como el denominador, cancelamos los factores comunes.

\[\begin{aligned} \frac{2 x^{2}+5 x-12}{4 x^{3}+16 x^{2}-9 x-36} &=\frac{(x+4)(2 x-3)}{(2 x+3)(2 x-3)(x+4)} \\ &=\frac{(x+4)(2 x-3)}{(2 x+3)(2 x-3)(x+4)} \\ &=\frac{1}{2 x+3} \end{aligned}\]

Ahora debemos determinar las restricciones. Esto quiere decir que debemos encontrar aquellos valores de x que hagan que cualquier denominador sea igual a cero.

• En el cuerpo de nuestro trabajo, tenemos el denominador (2x + 3) (2x − 3) (x + 4). Si establecemos esto igual a cero, la propiedad cero del producto implica que\[2 x+3=0 \quad \text { or } \quad 2 x-3=0 \quad \text { or } \quad x+4=0\]

Cada uno de estos factores lineales se puede resolver de forma independiente\[x=-3 / 2 \quad \text { or } \quad x=3 / 2 \quad \text { or } \quad x=-4\]

Cada uno de estos valores x es una restricción.

• En la expresión racional final, el denominador es 2x + 3. Esta expresión es igual a cero cuando x = −3/2 y no proporciona nuevas restricciones.
• Debido a que el denominador de la expresión original\(4 x^{3}+16 x^{2}-9 x-36\), es decir, es idéntico a su forma factorizada en el cuerpo nuestro trabajo, este denominador no producirá nuevas restricciones.

Así, para todos los valores de x\[\frac{2 x^{2}+5 x-12}{4 x^{3}+16 x^{2}-9 x-36}=\frac{1}{2 x+3}\]

siempre\(x \neq −3/2, 3/2, or −4\). Estas son las restricciones. Las dos expresiones son idénticas para todos los demás valores de x.

Por último, vamos a comprobar este resultado con nuestra calculadora gráfica. Cargue cada lado de la ecuación (18) en el menú Y=, como se muestra en la Figura\(\PageIndex{2}\) (a). Sabemos que tenemos una restricción en x = −3/2, así que vamos a establecer tblStart = −2 y\(\Delta \mathrm{Tbl}=0.5\), como se muestra en la Figura\(\PageIndex{2}\) (b). Asegúrese de tener AUTO establecido tanto para variables independientes como dependientes. Presione el botón TABLE para producir la pantalla tabular que se muestra en la Figura\(\PageIndex{2}\) (c).

Figura\(\PageIndex{2}\). Usando la calculadora gráfica para verificar que los lados izquierdo y derecho de la ecuación (18) son idénticos.

Recuerde que colocamos los lados izquierdo y derecho de la ecuación (18) en Y1 e Y2, respectivamente.

• En la Figura\(\PageIndex{2}\) (c), tenga en cuenta que las expresiones Y1 e Y2 coinciden en todos los valores de x excepto x = −1.5. Esta es la restricción −3/2 que encontramos anteriormente.
• Use la tecla de flecha hacia abajo para desplazarse hacia abajo en la tabla que se muestra en la Figura\(\PageIndex{2}\) (c) para producir la vista tabular que se muestra en la Figura\(\PageIndex{2}\) (d). Tenga en cuenta que Y1 e Y2 están de acuerdo para todos los valores de x excepto x = 1.5. Esta es la restricción 3/2 que encontramos anteriormente.
• Dejamos a nuestros lectores descubrir la restricción en x = −4 usando la uparrow para desplazarse hacia arriba en la tabla hasta alcanzar un valor x de −4. Debe descubrir otro mensaje ERR (error) en este valor x porque es una restricción. Obtienes el mensaje ERR debido a que el denominador del lado izquierdo de la ecuación (18) es cero en x = −4.

Cambios de Signo

No es raro que tengas que manipular los signos en una fracción para obtener factores comunes que luego puedan ser cancelados. Consideremos, por ejemplo, la expresión racional

\[\frac{3-x}{x-3}\]

Un enfoque posible es factografiar −1 fuera del numerador para obtener

\[\frac{3-x}{x-3}=\frac{-(x-3)}{x-3}\]

Ya puedes cancelar factores comunes.

\[\frac{3-x}{x-3}=\frac{-(x-3)}{x-3}=\frac{-(x-3)}{x-3}=-1\]

Este resultado es válido para todos los valores de x, siempre y cuando sea\(x \neq 3\).

Veamos otro ejemplo.

Ejemplo\(\PageIndex{6}\)

Reducir la expresión racional\[\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4}\] a los términos más bajos. Estado todas las restricciones.

Solución

En el numerador, factorizar 2x, luego completar la factorización usando la diferencia de patrón de dos cuadrados.

\[2 x-2 x^{3}=2 x\left(1-x^{2}\right)=2 x(1+x)(1-x)\]

El denominador puede ser factorizado por agrupación.

\[\begin{aligned} 3 x^{3}+4 x^{2}-3 x-4 &=x^{2}(3 x+4)-1(3 x+4) \\ &=\left(x^{2}-1\right)(3 x+4) \\ &=(x+1)(x-1)(3 x+4) \end{aligned}\]

Observe cómo se aplicó la diferencia de patrón de dos cuadrados en el último paso.

En este punto,\[\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4}=\frac{2 x(1+x)(1-x)}{(x+1)(x-1)(3 x+4)}\]

Debido a que tenemos 1 − x en el numerador y x − 1 en el denominador, vamos a factorizar un −1 de 1 − x, y debido a que el orden de los factores no afecta su producto, moveremos el −1 al frente del numerador.

\[\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4}=\frac{2 x(1+x)(-1)(x-1)}{(x+1)(x-1)(3 x+4)}=\frac{-2 x(1+x)(x-1)}{(x+1)(x-1)(3 x+4)}\]

Ahora podemos cancelar factores comunes.

\[\begin{aligned} \frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4} &=\frac{-2 x(1+x)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=\frac{-2 x(1+x)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=\frac{-2 x}{3 x+4} \end{aligned}\]

Tenga en cuenta que x + 1 es idéntico a 1 + x y cancela. Por lo tanto,

\[\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4}=\frac{-2 x}{3 x+4}\]

para todos los valores de x, siempre\(x \neq-1,1,\) o\(-4 / 3\). Estas son las restricciones, valores de x que hacen que los denominadores sean iguales a cero.

La regla de cambio de signo para fracciones

Veamos una aproximación alternativa al último ejemplo. Primero, compartamos el precepto de que cada fracción tiene tres signos, uno en el numerador, otro en el denominador y un tercero en la barra de fracciones. Por lo tanto,

\[\frac{-2}{3} \quad \text { has understood signs } \quad+\frac{-2}{+3}\]

Indiquemos la regla de cambio de signo para fracciones.

La regla de cambio de signo para fracciones

Cada fracción tiene tres signos, uno en el numerador, uno en el denominador y otro en la barra de fracciones. Si no ves un signo explícito, entonces se entiende un signo más. Si niega dos de estas partes,

• numerador y denominador, o
• numerador y barra de fracciones, o
• barra de fracción y denominador,

entonces la fracción permanece sin cambios.

Por ejemplo, comencemos con −2/3, luego hagamos dos negaciones: numerador y barra de fracciones. Entonces,

\[+\frac{-2}{+3}=-\frac{+2}{+3}, \quad \text { or with understood plus signs, } \quad \frac{-2}{3}=-\frac{2}{3}\]

Este es un resultado familiar, ya que negativo dos dividido por un tres positivo equivale a dos tercios negativos.

En otra nota, podríamos decidir negar numerador y denominador. Entonces −2/3 se convierte

\[+\frac{-2}{+3}=\frac{+2}{-3}, \quad \text { or with understood plus signs, } \quad \frac{-2}{3}=\frac{2}{-3}\]

Nuevamente, un resultado familiar. Ciertamente, dos negativos divididos por tres positivos es lo mismo que dos positivos divididos por tres negativos. Ambos igualan menos dos tercios.

Entonces ahí lo tienes. Niega dos partes cualesquiera de una fracción y ésta permanece sin cambios. En la superficie, esto parece un comentario trivial, pero se puede darle un buen uso a la hora de reducir expresiones racionales. Supongamos, por ejemplo, que tomamos la expresión racional original del Ejemplo\(\PageIndex{6}\) y negamos el numerador y la barra de fracciones.

\[\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4}=-\frac{2 x^{3}-2 x}{3 x^{3}+4 x^{2}-3 x-4}\]

Tenga en cuenta cómo hemos realizado dos cambios de señal. Hemos negado la barra de fracciones, hemos negado el numerador\(\left(-\left(2 x-2 x^{3}\right)=2 x^{3}-2 x\right)\), y hemos dejado solo el denominador. Por lo tanto, la fracción se mantiene sin cambios según nuestra regla de cambio de signo.

Ahora, factorizar y cancelar factores comunes (dejamos los pasos para nuestros lectores — son similares a los que tomamos en Ejemplo\(\PageIndex{6}\)).

\[\begin{aligned} \frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4} &=-\frac{2 x^{3}-2 x}{3 x^{3}+4 x^{2}-3 x-4} \\ &=-\frac{2 x(x+1)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=-\frac{2 x(x+1)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=-\frac{2 x}{3 x+4} \end{aligned}\]

Pero, ¿coincide esta respuesta con la respuesta en la ecuación (22)? Lo hace, como puede verse haciendo dos negaciones, barra de fracción y numerador.

\[-\frac{2 x}{3 x+4}=\frac{-2 x}{3 x+4}\]

La Línea Secante

Considera la gráfica de la función f que hemos dibujado en la Figura\(\PageIndex{3}\). Tenga en cuenta que hemos elegido dos puntos en la gráfica de f, a saber (a, f (a)) y (x, f (x)), y hemos dibujado una línea L a través de ellos que los matemáticos llaman la “línea secante”.

Figura\(\PageIndex{3}\). La línea secante pasa por (a, f (a)) y (x, f (x)).

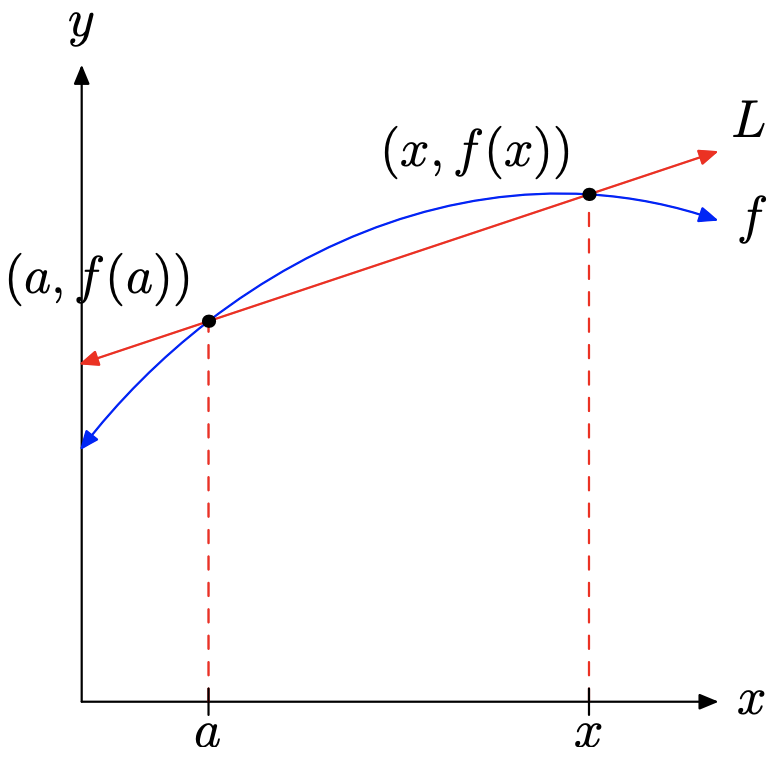
La pendiente de la línea secante L se encuentra dividiendo el cambio en y por el cambio en x.

\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{f(x)-f(a)}{x-a}\]

Esta pendiente proporciona la tasa promedio de cambio de la variable y con respecto a la variable x. Los estudiantes en cálculo utilizan esta “tasa promedio de cambio” para desarrollar la noción de “tasa instantánea de cambio”. Sin embargo, dejaremos esa tarea para los estudiantes de cálculo y nos concentraremos en el reto de simplificar la ecuación de expresión (23) para la tasa promedio de cambio.

Ejemplo\(\PageIndex{7}\)

Dada la función\(f(x) = x^2\), simplificar la expresión para la tasa promedio de cambio, a saber\[\frac{f(x)-f(a)}{x-a}\]

Solución

Primero, tenga en cuenta que\(f(x)=x^{2}\) y\(f(a)=a^{2},\) así podemos escribir\[\frac{f(x)-f(a)}{x-a}=\frac{x^{2}-a^{2}}{x-a}\]

Ahora podemos usar la diferencia de patrón de dos cuadrados para factorizar el numerador y cancelar factores comunes.

\[\frac{x^{2}-a^{2}}{x-a}=\frac{(x+a)(x-a)}{x-a}=x+a\]

Por lo tanto,\[\frac{f(x)-f(a)}{x-a}=x+a\]

siempre que, por supuesto, eso\(x \neq a\).

Veamos otro ejemplo.

Ejemplo\(\PageIndex{8}\)

Considera la función\(f(x)=x^{2}-3 x-5\). Simplificar\[\frac{f(x)-f(2)}{x-2}\]

Solución

Primero,\(f(x)=x^{2}-3 x-5\) y por lo\(f(2)=(2)^{2}-3(2)-5=-7,\) tanto para que podamos escribir

\[\frac{f(x)-f(2)}{x-2}=\frac{\left(x^{2}-3 x-5\right)-(-7)}{x-2}=\frac{x^{2}-3 x+2}{x-2}\]

Ahora podemos facetorizar el numerador y cancelar factores comunes.

\[\frac{x^{2}-3 x+2}{x-2}=\frac{(x-2)(x-1)}{x-2}=x-1\]

Así,\[\frac{f(x)-f(2)}{x-2}=x-1\] siempre y cuando, por supuesto, eso\(x \neq 2\).

Ejercicio

En los Ejercicios 1 - 12, reduzca cada número racional a términos más bajos aplicando los siguientes pasos:

1. Factor primo tanto numerador como denominador.
2. Cancelar factores primos comunes.
3. Simplifica el numerador y denominador del resultado.

Ejercicio\(\PageIndex{1}\)

\(\frac{147}{98}\)

Contestar

\(\frac{3}{2}\)

Ejercicio\(\PageIndex{2}\)

\(\frac{3087}{245}\)

Ejercicio\(\PageIndex{3}\)

\(\frac{1715}{196}\)

Contestar

\(\frac{35}{4}\)

Ejercicio\(\PageIndex{4}\)

\(\frac{225}{50}\)

Ejercicio\(\PageIndex{5}\)

\(\frac{1715}{441}\)

Contestar

\(\frac{35}{9}\)

Ejercicio\(\PageIndex{6}\)

\(\frac{56}{24}\)

Ejercicio\(\PageIndex{7}\)

\(\frac{108}{189}\)

Contestar

\(\frac{4}{7}\)

Ejercicio\(\PageIndex{8}\)

\(\frac{75}{500}\)

Ejercicio\(\PageIndex{9}\)

\(\frac{100}{28}\)

Contestar

\(\frac{25}{7}\)

Ejercicio\(\PageIndex{10}\)

\(\frac{98}{147}\)

Ejercicio\(\PageIndex{11}\)

\(\frac{1125}{175}\)

Contestar

\(\frac{45}{7}\)

Ejercicio\(\PageIndex{12}\)

\(\frac{3087}{8575}\)

En los Ejercicios 13 - 18, reducir la expresión dada a los términos más bajos. Estado todas las restricciones.

Ejercicio\(\PageIndex{13}\)

\(\frac{x^2−10x+9}{5x−5}\)

Contestar

\(\frac{x−9}{5}\), siempre\(x \ne 1\)

Ejercicio\(\PageIndex{14}\)

\(\frac{x^2−9x+20}{x^2−x−20}\)

Ejercicio\(\PageIndex{15}\)

\(\frac{x^2−2x−35}{x^2−7x}\)

Contestar

\(\frac{x+5}{x}\), siempre\(x \ne 0, 7\)

Ejercicio\(\PageIndex{16}\)

\(\frac{x^2−15x+54}{x^2+7x−8}\)

Ejercicio\(\PageIndex{17}\)

\(\frac{x^2+2x−63}{x^2+13x+42}\)

Contestar

\(\frac{(x−7)(x+9)}{(x+7)(x+6)}\), siempre\(x \ne −7, −6\)

Ejercicio\(\PageIndex{18}\)

\(\frac{x^2+13x+42}{9x+63}\)

En los Ejercicios 19 - 24, negar dos partes cualesquiera de la fracción, luego factorizar (si es necesario) y cancelar factores comunes para reducir la expresión racional a los términos más bajos. Estado todas las restricciones.

Ejercicio\(\PageIndex{19}\)

\(\frac{x+2}{−x−2}\)

Contestar

−1, siempre\(x \ne −2\)

Ejercicio\(\PageIndex{20}\)

\(\frac{4−x}{x−4}\)

Ejercicio\(\PageIndex{21}\)

\(\frac{2x−6}{3−x}\)

Contestar

−2, siempre\(x \ne 3\)

Ejercicio\(\PageIndex{22}\)

\(\frac{3x+12}{−x−4}\)

Ejercicio\(\PageIndex{23}\)

\(\frac{3x^2+6x}{−x−2}\)

Contestar

−3x, siempre\(x \ne −2\)

Ejercicio\(\PageIndex{24}\)

\(\frac{8x−2x^2}{x−4}\)

En los Ejercicios 25 - 38, reducir cada una de las expresiones racionales dadas a los términos más bajos. Estado todas las restricciones.

Ejercicio\(\PageIndex{25}\)

\(\frac{x^2−x−20}{25−x^2}\)

Contestar

\(−\frac{x+4}{x+5}\), siempre\(x \ne −5, 5\)

Ejercicio\(\PageIndex{26}\)

\(\frac{x−x^2}{x^2−3x+2}\)

Ejercicio\(\PageIndex{27}\)

\(\frac{x^2+3x−28}{x^2+5x−36}\)

Contestar

\(\frac{x+7}{x+9}\), siempre\(x \ne 4, −9\)

Ejercicio\(\PageIndex{28}\)

\(\frac{x^2+10x+9}{x^2+15x+54}\)

Ejercicio\(\PageIndex{29}\)

\(\frac{x^2−x−56}{8x−x^2}\)

Contestar

\(−\frac{x+7}{x}\), siempre\(x \ne 0, 8\)

Ejercicio\(\PageIndex{30}\)

\(\frac{x^2−7x+10}{5x−x^2}\)

Ejercicio\(\PageIndex{31}\)

\(\frac{x^2+13x+42}{x^2−2x−63}\)

Contestar

\(−\frac{x+6}{x−9}\), siempre\(x \ne −7, 9\)

Ejercicio\(\PageIndex{32}\)

\(\frac{x^2−16}{x^2−x−12}\)

Ejercicio\(\PageIndex{33}\)

\(\frac{x^2−9x+14}{49−x^2}\)

Contestar

\(−\frac{x−2}{x+7}\), siempre\(x \ne 7, −7\)

Ejercicio\(\PageIndex{34}\)

\(\frac{x^2+7x+12}{9−x^2}\)

Ejercicio\(\PageIndex{35}\)

\(\frac{x^2−3x−18}{x^2−6x+5}\)

Contestar

\(\frac{(x−6)(x+3)}{(x−1)(x−5)}\), siempre\(x \ne 1, 5\)

Ejercicio\(\PageIndex{36}\)

\(\frac{x^2+5x−6}{x^2−1}\)

Ejercicio\(\PageIndex{37}\)

\(\frac{x^2−3x−10}{−9x−18}\)

Contestar

\(−\frac{x−5}{9}\), siempre\(x \ne −2\)

Ejercicio\(\PageIndex{38}\)

\(\frac{x^2−6x+8}{16−x^2}\)

En los Ejercicios 39 - 42, reducir cada función racional a los términos más bajos, para luego realizar cada una de las siguientes tareas.

1. Cargue la expresión racional original en Y1 y la expresión racional reducida (su respuesta) en Y2 de su calculadora gráfica.
2. En TABLE SETUP, establezca TblStart igual a cero, ∆Tbl igual a 1, luego asegúrese de que tanto las variables independientes como las dependientes estén establecidas en Auto. Seleccione TABLE y desplácese con las flechas hacia arriba y hacia abajo en su calculadora hasta que se vea la restricción más pequeña. Copia ambas columnas de la tabla en tu trabajo de tarea, mostrando el acuerdo entre Y1 e Y2 y lo que sucede en todas las restricciones.

Ejercicio\(\PageIndex{39}\)

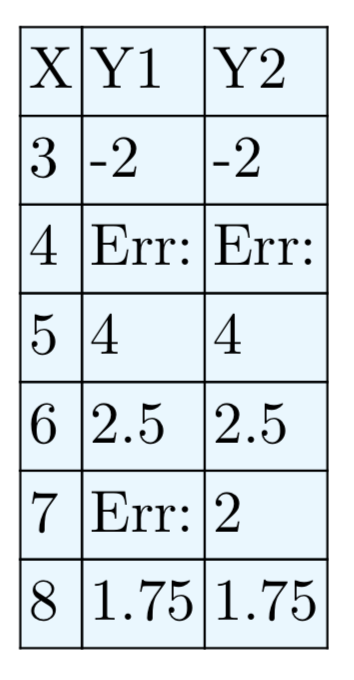
\(\frac{x^2−8x+7}{x^2−11x+28}\)

Contestar

\(\frac{x−1}{x−4}\), siempre\(x \ne 7, 4\)

Ejercicio\(\PageIndex{40}\)

\(\frac{x^2−5x}{x^2−9x}\)

Ejercicio\(\PageIndex{41}\)

\(\frac{8x−x^2}{x^2−x−56}\)

Contestar

\(−\frac{x}{x+7}\), siempre\(x \ne −7, 8\)

Ejercicio\(\PageIndex{42}\)

\(\frac{x^2+13x+40}{−2x−16}\)

Dado f (x) = 2x+5, simplifique cada una de las expresiones en los Ejercicios 43 - 46. Asegúrese de reducir su respuesta a los términos más bajos e indicar cualquier restricción.

Ejercicio\(\PageIndex{43}\)

\(\frac{f(x)−f(3)}{x−3}\)

Contestar

2, siempre\(x \ne 3\)

Ejercicio\(\PageIndex{44}\)

\(\frac{f(x)−f(6)}{x−6}\)

Ejercicio\(\PageIndex{45}\)

\(\frac{f(x)−f(a)}{x−a}\)

Contestar

2, siempre\(x \ne a\)

Ejercicio\(\PageIndex{46}\)

\(\frac{f(a+h)−f(a)}{h}\)

Dado\(f(x) = x^2+2x\), simplificar cada una de las expresiones en los Ejercicios 47 - 50. Asegúrese de reducir su respuesta a los términos más bajos e indicar cualquier restricción.

Ejercicio\(\PageIndex{47}\)

\(\frac{f(x)−f(1)}{x−1}\)

Contestar

x+3, siempre\(x \ne 1\)

Ejercicio\(\PageIndex{48}\)

\(\frac{f(x)−f(a)}{x−a}\)

Ejercicio\(\PageIndex{49}\)

\(\frac{f(a+h)−f(a)}{h}\)

Contestar

2a+h+2, siempre\(h \ne 0\)

Ejercicio\(\PageIndex{50}\)

\(\frac{f(x+h)−f(x)}{h}\)

Taladro para Habilidad. En los Ejercicios 51 - 54, evalúe la función dada en la expresión dada y simplifique su respuesta.

Ejercicio\(\PageIndex{51}\)

Supongamos que f es la función

\(f(x) = −\frac{x−6}{8x+7}\)

Evalúa f (−3x+2) y simplifica tu respuesta.

Contestar

\(−\frac{3x+4}{24x−23}\)

Ejercicio\(\PageIndex{52}\)

Supongamos que f es la función

\(f(x) = −\frac{5x+3}{7x+6}\)

Evalúa f (−5x+1) y simplifica tu respuesta.

Ejercicio\(\PageIndex{53}\)

Supongamos que f es la función

\(f(x) = −\frac{3x−6}{4x+6}\)

Evalúa f (−x−3) y simplifica tu respuesta.

Contestar

\(−\frac{3x+15}{4x+6}\)

Ejercicio\(\PageIndex{54}\)

Supongamos que f es la función

\(f(x) = \frac{4x−1}{2x−4}\)

Evalúa f (5x) y simplifica tu respuesta.

​​​​​​​