6.6E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112431

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

La práctica hace la perfección

Usar la propiedad Zero Product

En los siguientes ejercicios, resuelve.

1. $(3a−10)(2a−7)=0$

Responder: $a=\frac{10}{3},\; a=\frac{7}{2}$

2. $(5b+1)(6b+1)=0$

3. $6m(12m−5)=0$

Responder: $m=0,\; m=\frac{5}{12}$

4. $2x(6x−3)=0$

5. $(2x−1)^2=0$

Responder: $x=\frac{1}{2}$

6. $(3y+5)^2=0$

Resolver ecuaciones cuadráticas por factorización

En los siguientes ejercicios, resuelve.

7. $5a^2−26a=24$

Responder: $a=−\frac{4}{5},\; a=6$

8. $4b^2+7b=−3$

9. $4m^2=17m−15$

Responder: $m=\frac{5}{4},\; m=3$

10. $n^2=5−6n$

11. $7a^2+14a=7a$

Responder: $a=−1,\; a=0$

12. $12b^2−15b=−9b$

13. $49m^2=144$

Responder: $m=\frac{12}{7},\; m=−\frac{12}{7}$

14. $625=x^2$

15. $16y^2=81$

Responder: $y=−\frac{9}{4},\; y=\frac{9}{4}$

16. $64p^2=225$

17. $121n^2=36$

Responder: $n=−\frac{6}{11},\; n=\frac{6}{11}$

18. $100y^2=9$

19. $(x+6)(x−3)=−8$

Responder: $x=2,\; x=−5$

20. $(p−5)(p+3)=−7$

21. $(2x+1)(x−3)=−4x$

Responder: $x=\frac{3}{2},\; x=−1$

22. $(y−3)(y+2)=4y$

23. $(3x−2)(x+4)=12x$

Responder: $x=\frac{3}{2},\; x=−1$

24. $(2y−3)(3y−1)=8y$

25. $20x^2−60x=−45$

Responder: $x=−\frac{2}{3}$

26. $3y^2−18y=−27$

27. $15x^2−10x=40$

Responder: $x=2,\; x=−\frac{4}{3}$

28. $14y^2−77y=−35$

29. $18x^2−9=−21x$

Responder: $x=−\frac{3}{2},\; x=\frac{1}{3}$

30. $16y^2+12=−32y$

31. $16p^3=24p^2-9p$

Responder: $p=0,\; p=\frac{3}{4}$

32. $m^3−2m^2=−m$

33. $2x^3+72x=24x^2$

Responder: $x=0,\space x=6$

34. $3y^3+48y=24y^2$

35. $36x^3+24x^2=−4x$

Responder: $x=0,\space x=\frac{1}{3}$

36. $2y^3+2y^2=12y$

Resolver ecuaciones con funciones polinómicas

En los siguientes ejercicios, resuelve.

37. Para la función,$f(x)=x^2−8x+8$, ⓐ find when$f(x)=−4$ ⓑ Usa esta información para encontrar dos puntos que se encuentran en la gráfica de la función.

Responder: ⓐ$x=2$ o$x=6$ ⓑ$(2,−4)$$(6,−4)$

38. Para la función,$f(x)=x^2+11x+20$, ⓐ find when$f(x)=−8$ ⓑ Usa esta información para encontrar dos puntos que se encuentran en la gráfica de la función.

39. Para la función,$f(x)=8x^2−18x+5$, ⓐ find when$f(x)=−4$ ⓑ Usa esta información para encontrar dos puntos que se encuentran en la gráfica de la función.

Responder: ⓐ$x=\frac{3}{2}$ o$x=\frac{3}{4}$
ⓑ$(\frac{3}{2},−4)$$(\frac{3}{4},−4)$

40. Para la función,$f(x)=18x^2+15x−10$, ⓐ find when$f(x)=15$ ⓑ Usa esta información para encontrar dos puntos que se encuentran en la gráfica de la función.

En los siguientes ejercicios, para cada función, encuentra: ⓐ los ceros de la función ⓑ las$x$ -intercepciones de la gráfica de la función ⓒ la$y$ -intercepción de la gráfica de la función.

41. $f(x)=9x^2−4$

42. $f(x)=25x^2−49$

43. $f(x)=6x^2−7x−5$

44. $f(x)=12x^2−11x+2$

Resolver aplicaciones modeladas por ecuaciones cuadráticas

En los siguientes ejercicios, resuelve.

45. El producto de dos enteros impares consecutivos es$143$. Encuentra los enteros.

Responder: $−13,\space −11$y$11,\space 13$

46. El producto de dos enteros impares consecutivos es$195$. Encuentra los enteros.

47. El producto de dos enteros pares consecutivos es$168$. Encuentra los enteros.

Responder: $−14,\space −12$y$12,\space 14$

48. El producto de dos enteros pares consecutivos es$288$. Encuentra los enteros.

49. El área de una alfombra rectangular es de pies$28$ cuadrados. El largo es tres pies más que el ancho. Encuentra el largo y el ancho de la alfombra.

Responder: $−4$y$7$

50. Un muro de contención rectangular tiene área de pies$15$ cuadrados. La altura de la pared es dos pies menos que su longitud. Encuentra la altura y la longitud de la pared.

51. El área de un tablón de anuncios es de pies$55$ cuadrados. La longitud es de cuatro pies menos que tres veces el ancho. Encuentra la longitud y el ancho de un tablón de anuncios.

Responder: $5,\space 11$

52. Una cochera rectangular tiene área de pies$150$ cuadrados. La altura de la cochera es de cinco pies menos del doble de su longitud. Encuentra la altura y la longitud de la cochera.

53. Un banderín tiene forma de triángulo rectángulo, con$10$ pies de hipotenusa. La longitud de un lado del banderín es dos pies más larga que la longitud del otro lado. Encuentra la longitud de los dos lados del banderín.

Responder: $6,\space 8$

54. Un vitral tiene forma de triángulo rectángulo. La hipotenusa es$15$ feet. One leg is three more than the other. Find the lengths of the legs.

55. Una piscina reflectante tiene forma de triángulo rectángulo, con una pata a lo largo de la pared de un edificio. La hipotenusa es$9$ pies más larga que el costado a lo largo del edificio. El tercer lado es$7$ pies más largo que el lado a lo largo del edificio. Encuentra las longitudes de los tres lados de la piscina reflectante.

Responder: $8,\space 15,\space 17$

56. Un recinto de cabras tiene la forma de un triángulo rectángulo. Una pata del recinto está construida contra el costado del granero. La otra pierna es$4$ pies más que la pierna contra el granero. La hipotenusa es$8$ pies más que la pierna a lo largo del granero. Encuentra los tres lados del recinto de cabras.

57. Juli va a lanzar un cohete modelo en su patio trasero. Cuando lanza el cohete, la función$h(t)=−16t^2+32t$ modela la altura$h$,, del cohete sobre el suelo en función del tiempo,$t$. Encuentra:

ⓐ los ceros de esta función que nos indica cuándo el cohete chocará contra el suelo. ⓑ el tiempo en que el cohete estará a$16$ pies sobre el suelo.

Responder: ⓐ 0, 2 ⓑ 1

58. Gianna va a lanzar una pelota desde el último piso de su secundaria. Cuando lanza la pelota desde$48$ pies sobre el suelo, la función$h(t)=−16t^2+32t+48$ modela la altura$h$,, de la pelota sobre el suelo en función del tiempo,$t$. Encuentra:

ⓐ los ceros de esta función la cual nos indica cuándo la pelota golpeará el suelo. ⓑ el (los) tiempo (es) en el que la pelota estará a$48$ pies sobre el suelo. ⓒ la altura que tendrá la pelota a los$t=1$ segundos que es cuando la pelota estará en su punto más alto.

Ejercicios de escritura

59. Explica cómo resuelves una ecuación cuadrática. ¿Cuántas respuestas esperas obtener para una ecuación cuadrática?

Responder: Las respuestas variarán.

60. Dar un ejemplo de una ecuación cuadrática que tiene un GCF y ninguna de las soluciones a la ecuación es cero.

Autocomprobación

ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.

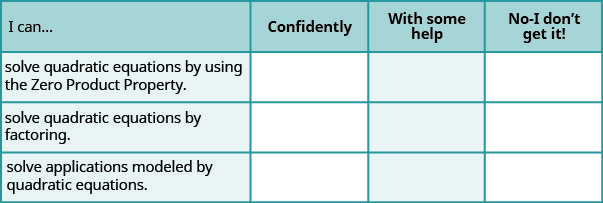
$Esta tabla tiene 4 columnas, 3 filas y una fila de cabecera. La fila de encabezado etiqueta cada columna: Puedo, con confianza, con algo de ayuda y no, no lo consigo. La primera columna tiene las siguientes afirmaciones: resolver ecuaciones cuadráticas usando la propiedad cero del producto, resolver ecuaciones cuadráticas por factorización y resolver aplicaciones modeladas por ecuaciones cuadráticas.$

ⓑ En general, después de mirar la lista de verificación, ¿crees que estás bien preparado para la siguiente sección? ¿Por qué o por qué no?

Search

Text Color

Text Size

Margin Size

Font Type