11.2: Completar la Plaza
- Page ID
- 117426
Al resolver ecuaciones cuadráticas previamente (entonces conocidas como ecuaciones trinomiales), factorizamos para resolver. Sin embargo, recuerde, no todas las ecuaciones son factorizables. Considera la ecuación\(x^2 − 2x − 7 = 0\). Esta ecuación no es factorizable, pero hay dos soluciones a esta ecuación:\(1 + 2\sqrt{2}\) y\(1 − 2\sqrt{2}\). Al observar la forma de estas soluciones, obtuvimos este tipo de soluciones en la sección anterior mientras usábamos la propiedad raíz cuadrada. Si podemos obtener un cuadrado perfecto, entonces podemos aplicar la propiedad de raíz cuadrada y resolver como de costumbre. Este método que utilizamos para obtener un cuadrado perfecto se llama completar el cuadrado.
Recordar. Fórmulas de productos especiales para trinomios cuadrados perfectos:
\[(a+b)^2=a^2+2ab+b^2\quad\text{or}\quad (a-b)^2=a^2-2ab+b^2\nonumber\]
Utilizamos estas fórmulas para ayudarnos a resolver completando el cuadrado.
Completa La Plaza
Primero comenzamos completando el cuadrado y reescribiendo el trinomio en forma factorizada usando las fórmulas trinomiales cuadradas perfectas.
Completa el cuadrado encontrando\(c\):\(x^2+8x+c\)
Solución
Hay un par de formas de completar la plaza. La primera forma es pensar mentalmente en un número para\(c\) tal que podamos factorizar el trinomio como trinomio cuadrado perfecto, es decir,
\[x^2+8x+c=(x+\underline{\quad} )^2\nonumber\]
Algunos podrían ver que este número\(c = 16\) si están interesados en factorizar. Aviso,\((x + 4)^2 = x^2 + 8x + 16\). Otra forma es, literalmente, completar el cuadrado:
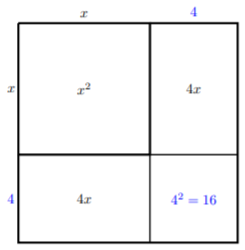
Observe que el cuadrado tiene todos los componentes del trinomio cuadrado perfecto. De ahí que podamos ver las dimensiones de esta plaza para ser
\[(x+4)\times (x+4)\nonumber\]
que es
\[(x+4)^2\nonumber\]
y el coeficiente constante que falta es\(16\), el cuadrado de\(4\). El uso de uno de estos métodos será suficiente dependiendo del tipo de alumno. Algunos estudiantes disfrutan de la relación geométrica entre la ecuación cuadrática y el cuadrado, y algunos disfrutan del método algebraico. Corresponde a la discreción del alumno.
Así, vemos\(c = 16\) y se factoriza el trinomio\(x^2 + 8x + \color{blue}{16}\) cuadrado perfecto\((x + 4)^2\).
En Ejemplo 11.2.1 , el aviso\(c\) se derivó del término medio\(8x\). Al mirar el cuadrado, vemos que el coeficiente del término lineal se\(8\) dividió en medio y cuadrado (porque estábamos encontrando el área del cuadrado inferior derecho). Este es exactamente el método que utilizamos para todos los problemas a la hora de completar el cuadrado.
Para completar el cuadrado de cualquier trinomio, siempre cuadramos la mitad del coeficiente del término lineal, es decir,
\[\left(\dfrac{b}{2}\right)^2\quad\text{or}\quad\left(\dfrac{1}{2}b\right)^2\nonumber\]
Usualmente usamos la segunda expresión cuando el coeficiente del término medio es una fracción.
Completa el cuadrado encontrando\(c\):\(x^2-7x+c\)
Solución
Para obtener\(c\), utilizamos la fórmula anterior\(\left(\dfrac{b}{2}\right)^2\).
\[\begin{array}{rl} x^2-7x+\color{blue}{c}&\color{black}{b}=-7;\text{ apply formula }\left(\dfrac{b}{2}\right)^2 \\ x^2-7x+\color{blue}{\left(\dfrac{-7}{2}\right)^2}&\color{black}{\text{Simplify }}c\\ x^2-7x+\color{blue}{\dfrac{49}{4}}&\color{black}{\text{Perfect square trinomial}}\end{array}\nonumber\]
Por lo tanto,\(c=\dfrac{49}{4}\). Reescribiendo este trinomio cuadrado perfecto en forma factorizada, obtenemos
\[x^2-7x+\color{blue}{\dfrac{49}{4}}\color{black}{=}\left(x-\dfrac{7}{2}\right)^2\nonumber\]
Completa el cuadrado encontrando\(c\):\(x^2+\dfrac{5}{3}x+c\)
Solución
Para obtener\(c\), utilizamos la fórmula anterior\(\left(\dfrac{1}{2}b\right)^2\) ya que el coeficiente del término lineal es una fracción.
\[\begin{array}{rl} x^2+\dfrac{5}{3}x+\color{blue}{c}&\color{black}{b}=\dfrac{5}{3};\text{ apply formula }\left(\dfrac{1}{2}b\right)^2 \\ x^2+\dfrac{5}{3}x+\color{blue}{\left(\dfrac{1}{2}\cdot\dfrac{5}{3}\right)^2}&\color{black}{\text{Simplify }}c \\ x^2+\dfrac{5}{3}x+\color{blue}{\dfrac{25}{36}}&\color{black}{\text{Perfect square polynomial}}\end{array}\nonumber\]
Por lo tanto,\(c=\dfrac{25}{36}\). Reescribiendo este trinomio cuadrado perfecto en forma factorizada, obtenemos
\[x^2+\dfrac{5}{3}x+\color{blue}{\dfrac{25}{36}}\color{black}{=}\left(x+\dfrac{5}{6}\right)^2\nonumber\]
Los chinos en el 200 a.C. fueron el primer grupo de cultivo conocido en utilizar un método similar al de completar el cuadrado, pero su método solo se utilizó para calcular raíces positivas.
Dada una ecuación cuadrática\(x^2 + bx + c = 0\), podemos usar el siguiente método para resolver para\(x\).
Paso 1. Reescribe la ecuación cuadrática para que el coeficiente del término inicial sea uno, y el coeficiente constante original esté en el lado opuesto del signo igual de los términos inicial y lineal.
Paso 2. Completa el cuadrado, es decir,\(\left(\dfrac{b}{2}\right)^2\) o\(\left(\dfrac{1}{2}b\right)^2\), y agrega el resultado a ambos lados de la ecuación cuadrática.
Paso 3. Reescribe el trinomio cuadrado perfecto en forma factorizada.
Paso 4. Resuelve usando la propiedad raíz cuadrada.
Paso 5. Verificar la (s) solución (es).
Resolver ecuaciones cuadráticas completando el cuadrado,\(a=1\)
Recordar. Cuando el coeficiente inicial es uno, es decir,\(a = 1\), de la ecuación cuadrática\(ax^2 + bx + c = 0\), tenemos la ecuación cuadrática\(x^2 + bx + c = 0\).
Resolver:\(x^2+10x=-24\)
Solución
Paso 1. Reescribe la ecuación cuadrática para que el coeficiente del término inicial sea uno, y el coeficiente constante original esté en el lado opuesto del signo igual de los términos inicial y lineal. Aviso, el primer paso está hecho por nosotros:\[x^2+10x=-24\nonumber\]
Paso 2. Completa el cuadrado, es decir,\(\left(\dfrac{b}{2}\right)^2\) o\(\left(\dfrac{1}{2}b\right)^2\), y agrega el resultado a ambos lados de la ecuación cuadrática. \[\begin{array}{rl} x^2+10x=-24 &b=10;\text{ apply formula }\left(\dfrac{b}{2}\right)^2 \\ x^2+10x+\color{blue}{\left(\dfrac{10}{2}\right)^2}\color{black}{=}-24+\color{blue}{\left(\dfrac{10}{2}\right)^2}&\color{black}{\text{Simplify}} \\ x^2+10x+\color{blue}{25}\color{black}{=}-24+\color{blue}{25}&\color{black}{\text{Perfect square trinomial}}\end{array}\nonumber\]
Paso 3. Reescribe el trinomio cuadrado perfecto en forma factorizada. \[\begin{array}{rl}x^2+10x+25=-24+25 &\text{Perfect square trinomial} \\ (x+5)^2=1 &\text{Factored form}\end{array}\nonumber\]
Paso 4. Resuelve usando la propiedad raíz cuadrada. \[\begin{array}{rl} (x+5)^2=1&\text{Apply the square root property} \\ x+5=\pm\sqrt{1}&\text{Isolate the variable} \\ x=-5\pm\sqrt{1}&\text{Rewrite as two solutions} \\ x=-5+1\text{ or }x=-5-1&\text{Evaluate} \\ x=-4\text{ or }x=-6&\text{Solution}\end{array}\nonumber\]
Paso 5. Verificar la (s) solución (es). \[\begin{array}{rl}x^2+10x=-24&x^2+10x=-24\quad \\ \color{blue}{(-4)}\color{black}{^2}+10\color{blue}{(-4)}\color{black}{\stackrel{?}{=}}-24&\color{blue}{(-6)}\color{black}{^2}+10\color{blue}{(-6)}\color{black}{\stackrel{?}{=}}-24\quad \\ 16-40\stackrel{?}{=}-24&36-60\stackrel{?}{=}-24\quad \\ -24=-24\:\checkmark & -24=-24\:\checkmark \end{array}\nonumber\]
Así,\(x = −4\) y\(x = −6\) son las soluciones.
Resolver:\(n^2+8n+4=0\)
Solución
Paso 1. Reescribe la ecuación cuadrática para que el coeficiente del término inicial sea uno, y el coeficiente constante original esté en el lado opuesto del signo igual de los términos inicial y lineal. \[\begin{aligned}n^2+8n+4&=0 \\ n^2+8n&=-4\end{aligned}\]
Paso 2. Completa el cuadrado, es decir,\(\left(\dfrac{b}{2}\right)^2\) o\(\left(\dfrac{1}{2}b\right)^2\), y agrega el resultado a ambos lados de la ecuación cuadrática. \[\begin{array}{rl}n^2-8n=-4 &b=-8;\text{ apply formula }\left(\dfrac{b}{2}\right)^2 \\ n^2-8n+\color{blue}{\left(\dfrac{-8}{2}\right)^2}\color{black}{=}-4+\color{blue}{\left(\dfrac{-8}{2}\right)^2}&\color{black}{\text{Simplify}} \\ n^2-8n+\color{blue}{16}\color{black}{=}-4+\color{blue}{16}&\color{black}{\text{Perfect square trinomial}}\end{array}\nonumber\]
Paso 3. Reescribe el trinomio cuadrado perfecto en forma factorizada. \[\begin{array}{rl} n^2-8n+16=-4+16&\text{Perfect square trinomial} \\ (n-4)^2=12&\text{Factored form}\end{array}\nonumber\]
Paso 4. Resuelve usando la propiedad raíz cuadrada. \[\begin{array}{rl}(n-4)^2=12 &\text{Apply the square root property} \\ n-4=\pm\sqrt{12}&\text{Isolate the variable} \\ n=4\pm\sqrt{12}&\text{Simplify }\sqrt{12} \\ n=4\pm\sqrt{4\cdot 3}&\text{Apply product property for radicals} \\ n=4\pm 2\sqrt{3}&\text{Solution}\end{array}\nonumber\]
Paso 5. Verificar la (s) solución (es). Dejamos este paso al alumno.
Así,\(n=4+2\sqrt{3}\) y\(n=4-2\sqrt{3}\) son las soluciones.
Resolver ecuaciones cuadráticas completando el cuadrado,\(a\neq 1\)
Resolver:\(3x^2-36x+60=0\)
Solución
Paso 1. Reescribe la ecuación cuadrática para que el coeficiente del término inicial sea uno, y el coeficiente constante original esté en el lado opuesto del signo igual de los términos inicial y lineal. \[\begin{aligned} 3x^2-36x+60&=0 \\ 3x^2-36x&=-60 \\ \color{blue}{3}\color{black}{(}x^2-12x)&=\color{blue}{3}\color{black}{\cdot}-20 \\ \color{black}{\cancel{\color{blue}{3}}}\color{black}{(}x^2-12x)&=\color{black}{\cancel{\color{blue}{3}}}\color{black}{\cdot}-20 \\ x^2-12x&=-20\end{aligned}\]
Paso 2. Completa el cuadrado, es decir,\(\left(\dfrac{b}{2}\right)^2\) o\(\left(\dfrac{1}{2}b\right)^2\), y agrega el resultado a ambos lados de la ecuación cuadrática. \[\begin{array}{rl}x^2-12x=-20 &b=-12;\text{ apply formula }\left(\dfrac{b}{2}\right)^2 \\ x^2-12x+\color{blue}{\left(\dfrac{-12}{2}\right)^2}\color{black}{=}-20+\color{blue}{\left(\dfrac{-12}{2}\right)^2}&\color{black}{\text{Simplify}} \\ x^2-12x+\color{blue}{36}\color{black}{=}-20+\color{blue}{36}&\color{black}{\text{Perfect square trinomial}}\end{array}\nonumber\]
Paso 3. Reescribe el trinomio cuadrado perfecto en forma factorizada. \[\begin{array}{rl}x^2-12x+36=-20+36&\text{Perfect square trinomial} \\ (x-6)^2=16&\text{Factored form}\end{array}\nonumber\]
Paso 4. Resuelve usando la propiedad raíz cuadrada. \[\begin{array}{rl}(x-6)^2=16&\text{Apply the square root property} \\ x-6=\pm\sqrt{16}&\text{Isolate the variable} \\ x=6\pm\sqrt{16}&\text{Rewrite as two solutions} \\ x=6+4\text{ or }x=6-4&\text{Evaluate} \\ x=10\text{ or }x=2&\text{Solution}\end{array}\nonumber\]
Paso 5. Verificar la (s) solución (es). Dejamos este paso al alumno.
Así,\(x=10\) y\(x=2\) son las soluciones.
Resolver:\(2k^2+k-2=0\)
Solución
Paso 1. Reescribe la ecuación cuadrática para que el coeficiente del término inicial sea uno, y el coeficiente constante original esté en el lado opuesto del signo igual de los términos inicial y lineal. \[\begin{aligned} 2k^2+k-2&=0 \\ 2k^2+k&=2 \\ \color{blue}{2}\color{black}{}\left(k^2+\dfrac{1}{2}k\right)&=\color{blue}{2}\color{black}{\:\cdot}1 \\ \color{black}{\cancel{\color{blue}{2}}}\color{black}{}\left(k^2+\dfrac{1}{2}k\right)&=\color{black}{\cancel{\color{blue}{2}}}\color{black}{\:\cdot} 1 \\ k^2+\dfrac{1}{2}k&=1\end{aligned}\]
Paso 2. Completa el cuadrado, es decir,\(\left(\dfrac{b}{2}\right)^2\) o\(\left(\dfrac{1}{2}b\right)^2\), y agrega el resultado a ambos lados de la ecuación cuadrática. \[\begin{array}{rl} k^2+\dfrac{1}{2}k=1 &b=\dfrac{1}{2};\text{ apply formula }\left(\dfrac{1}{2}b\right)^2 \\ k^2+\dfrac{1}{2}k+\color{blue}{\left(\dfrac{1}{2}\cdot\dfrac{1}{2}\right)^2}\color{black}{=}1+\color{blue}{\left(\dfrac{1}{2}\cdot\dfrac{1}{2}\right)^2}&\color{black}{\text{Simplify}} \\ k^2+\dfrac{1}{2}k+\color{blue}{\dfrac{1}{16}}\color{black}{=}1+\color{blue}{\dfrac{1}{16}}&\color{black}{\text{Perfect square trinomial}}\end{array}\nonumber\]
Paso 3. Reescribe el trinomio cuadrado perfecto en forma factorizada. \[\begin{array}{rl}k^2+\dfrac{1}{2}k+\dfrac{1}{16}=1+\dfrac{1}{16}&\text{Perfect square trinomial} \\ \left(k+\dfrac{1}{4}\right)^2=\dfrac{17}{16}&\text{Factored form}\end{array}\nonumber\]
Paso 4. Resuelve usando la propiedad raíz cuadrada. \[\begin{array}{rl}\left(k+\dfrac{1}{4}\right)^2=\dfrac{17}{16}&\text{Apply the square root property} \\ k+\dfrac{1}{4}=\pm\sqrt{\dfrac{17}{16}}&\text{Isolate the variable} \\ k=-\dfrac{1}{4}\pm\sqrt{\dfrac{17}{16}}&\text{Simplify }\sqrt{\dfrac{17}{16}} \\ k=-\dfrac{1}{4}\pm\dfrac{\sqrt{14}}{4}&\text{Same denominator, combine fractions} \\ k=\dfrac{-1\pm\sqrt{17}}{4}&\text{Solution}\end{array}\nonumber\]
Paso 5. Verificar la (s) solución (es). Dejamos este paso al alumno.
Así,\(\dfrac{-1+\sqrt{17}}{4}\) y\(\dfrac{-1-\sqrt{17}}{4}\) son las soluciones.
Completar la tarea cuadrada
Completa el cuadrado y vuelve a escribir en forma factorizada.
\(x^2-30x+\underline{\quad}\)
\(m^2-36m+\underline{\quad}\)
\(x^2-15x+\underline{\quad}\)
\(y^2-y+\underline{\quad}\)
\(a^2-24a+\underline{\quad}\)
\(x^2-34x+\underline{\quad}\)
\(r^2-\dfrac{1}{9}r+\underline{\quad}\)
\(p^2-17p+\underline{\quad}\)
Resuelve cada ecuación completando el cuadrado.
\(x^2-16x+55=0\)
\(v^2-8v+45=0\)
\(6x^2+12x+63=0\)
\(5k^2-10k+48=0\)
\(x^2+10x-57=4\)
\(n^2-16n+67=4\)
\(2x^2+4x+38=-6\)
\(8b^2+16b-37=5\)
\(x^2=-10x-29\)
\(n^2=-21+10n\)
\(3k^2+9=6k\)
\(2x^2+63=8x\)
\(p^2-8p=-55\)
\(7n^2-n+7=7n+6n^2\)
\(13b^2+15b+44=-5+7b^2+3b\)
\(5x^2+5x=-31-5x\)
\(v^2+5v+28=0\)
\(7x^2-6x+40=0\)
\(k^2-7k+50=3\)
\(5x^2+8x-40=8\)
\(m^2=-15+9m\)
\(8r^2+10r=-55\)
\(-2x^2+3x-5=-4x^2\)
\(5n^2-8n+60=-3n+6+4n^2\)
\(n^2-8n-12=0\)
\(b^2+2b+43=0\)
\(3x^2-6x+47=0\)
\(8a^2+16a-1=0\)
\(p^2-16p-52=0\)
\(m^2-8m-3=0\)
\(6r^2+12r-24=-6\)
\(6n^2-12n-14=4\)
\(v^2=14v+36\)
\(a^2-56=-10a\)
\(5x^2=-26+10x\)
\(5n^2=-10n+15\)
\(x^2+8x+15=8\)
\(n^2+4n=12\)
\(-3r^2+12r+49=-6r^2\)
\(8n^2+16n=64\)
\(b^2+7b-33=0\)
\(4x^2+4x+25=0\)
\(a^2-5a+25=3\)
\(2p^2-p+56=-8\)
\(n^2-n=-41\)
\(3x^2-11x=-18\)
\(4b^2-15b+56=3b^2\)
\(10v^2-15v=27+4v^2-6v\)


