2.2: Simplificar expresiones algebraicas

Última actualización
Guardar como PDF

Page ID: 110143

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Aplicar la propiedad distributiva para simplificar una expresión algebraica.
Identificar y combinar términos similares.

Propiedad distributiva

Las propiedades de los números reales son importantes en nuestro estudio del álgebra porque una variable es simplemente una letra que representa un número real. En particular, el bien distributivo establece que dado cualquier número real$a, b,$ y$c$,

\[\color{Cerulean}{a}\color{black}{(b+c)=}\color{Cerulean}{a}\color{black}{b+}\color{Cerulean}{a}\color{black}{c}\]

Esta propiedad se aplica al simplificar expresiones algebraicas. Para demostrar cómo se usa, simplificamos de dos$2(5−3)$ maneras, y observamos el mismo resultado correcto.

Ciertamente, si se puede simplificar el contenido de los paréntesis, hágalo primero. Por otra parte, cuando no se pueda simplificar el contenido de paréntesis, multiplique cada término dentro de los paréntesis por el factor fuera de los paréntesis utilizando la propiedad distributiva. Aplicar la propiedad distributiva permite multiplicar y eliminar los paréntesis.

Ejemplo$\PageIndex{1}$

Simplificar:

$5(7y+2)$.

Solución:

$5$Multiplica por cada término dentro de los paréntesis.

$\begin{aligned}\color{Cerulean}{5}\color{black}{(7y+2)}&=\color{Cerulean}{5}\color{black}{\cdot 7y+}\color{Cerulean}{5}\color{black}{\cdot 2} \\ &=35y+10 \end{aligned}$

Respuesta:

$35y+10$

Ejemplo$\PageIndex{2}$

Simplificar:

$−3(2x^{2}+5x+1)$.

Solución:

$−3$Multiplica por cada uno de los coeficientes de los términos dentro de los paréntesis.

Respuesta:

$-6x^{2}-15x-3$

Ejemplo$\PageIndex{3}$

Simplificar:

$5(−2a+5b)−2c$.

Solución:

Aplicar la propiedad distributiva multiplicando solo los términos agrupados dentro de los paréntesis por$5$.

$Captura de pantalla (749) .png$

Figura$\PageIndex{1}$

Respuesta:

$-10a+25b-2c$

Debido a que la multiplicación es conmutativa, también podemos escribir la propiedad distributiva de la siguiente manera:

\[(b+c)a=ba+ca\]

Ejemplo$\PageIndex{4}$

Simplificar:

$(3x−4y+1)⋅3$.

Solución:

Multiplique cada término dentro de los paréntesis por$3$.

$\begin{aligned} (3x-4y+1)\cdot 3&=3x\color{Cerulean}{\cdot 3}\color{black}{-4y}\color{Cerulean}{\cdot 3}\color{black}{+1}\color{Cerulean}{\cdot 3} \\ &=9x-12y+3 \end{aligned}$

Respuesta:

$9x-12y+3$

La división en álgebra a menudo se indica usando la barra de fracciones en lugar de con el símbolo ($÷$). Y a veces es útil reescribir expresiones que implican división como productos:

$\begin{array}{c}{\color{black}{\frac{x}{\color{Cerulean}{5}}=\frac{1x}{5}=\color{Cerulean}{\frac{1}{5}}\color{black}{\cdot x}}} \\{\color{black}{\frac{\color{Cerulean}{3}\color{black}{ab}}{\color{Cerulean}{7}}=\frac{3}{7}\cdot \frac{ab}{1}=\color{Cerulean}{\frac{3}{7}}\color{black}{\cdot ab}}}\\{\frac{x+y}{\color{Cerulean}{3}}=\frac{1}{3}\cdot \frac{(x+y)}{1}=\color{Cerulean}{\frac{1}{3}}\color{black}{\cdot (x+y)}} \end{array}$

Reescribir expresiones algebraicas como productos nos permite aplicar la propiedad distributiva.

Ejemplo$\PageIndex{5}$

Dividir:

\ (\ frac {25x^ {2} -5x+10} {5}.

Solución:

Primero, tratar esto como$\frac{1}{5}$ veces la expresión en el numerador y luego distribuir.

$\begin{aligned} \frac{25x^{2}-5x+10}{\color{Cerulean}{5}}&=\frac{1}{5}\cdot\frac{(25x^{2}-5x+10)}{1} \\ &=\color{Cerulean}{\frac{1}{5}}\color{black}{\cdot (25x^{2}-5x+10)} &\color{Cerulean}{Multiply\:each\:term\:by\:\frac{1}{5}.} \\ &=\color{Cerulean}{\frac{1}{5}}\color{black}{\cdot 25x^{2}-}\color{Cerulean}{\frac{1}{5}}\color{black}{\cdot 5x+}\color{Cerulean}{\frac{1}{5}}\color{black}{\cdot 10}&\color{Cerulean}{Simplify.} \\ &=5x^{2}-x+2 \end{aligned}$

Solución alternativa:

Piense en$5$ como un denominador común y divida cada uno de los términos en el numerador por$5$:

$\begin{aligned} \frac{25x^{2}-5x+10}{5}&=\frac{25x^{2}}{5}-\frac{5x}{5}+\frac{10}{5} \\ &=5x^{2}-x+2 \end{aligned}$

Respuesta:

$5x^{2}-x+2$

Discutiremos la división de las expresiones algebraicas con más detalle a medida que avancemos en el curso.

Ejercicio$\PageIndex{1}$

Simplificar:

$\frac{1}{3}(−9x+27y−3)$.

Contestar: $-3x+9y-1$

Combinando términos similares

Los términos con las mismas partes variables se denominan términos similares o términos similares. Además, los términos constantes se consideran como términos similares. Si una expresión algebraica contiene términos similares, aplique la propiedad distributiva de la siguiente manera:

$\begin{array}{c}{2\color{Cerulean}{a}\color{black}{+3}\color{Cerulean}{a}\color{black}{=(2+3)}\color{Cerulean}{a}\color{black}{=5}\color{Cerulean}{a}}\\{7\color{Cerulean}{xy}\color{black}{-5}\color{Cerulean}{xy}\color{black}{=(7-5)}\color{Cerulean}{xy}\color{black}{=2}\color{Cerulean}{xy}}\\{10\color{Cerulean}{x^{2}}\color{black}{+4}\color{Cerulean}{x^{2}}\color{black}{-6}\color{Cerulean}{x^{2}}\color{black}{=(10+4-6)}\color{Cerulean}{x^{2}}\color{black}{=8}\color{Cerulean}{x^{2}}} \end{array}$

Es decir, si las partes variables de términos son exactamente las mismas, entonces podemos sumar o restar los coeficientes para obtener el coeficiente de un solo término con la misma parte variable. A este proceso se le llama combinar términos similares. Por ejemplo,

$3a^{2}b+2a^{2}b=5a^{2}b$

Observe que los factores variables y sus exponentes no cambian. Combinar términos similares de esta manera, para que la expresión no contenga otros términos similares, se llama simplificar la expresión. Usa esta idea para simplificar expresiones algebraicas con múltiples términos similares.

Ejemplo$\PageIndex{6}$

Simplificar:

$3a+2b−4a+9b$.

Solución:

Identifica los términos similares y combínalos.

$\begin{aligned} 3a+2b-4a+9b&=3\color{Cerulean}{a}\color{black}{-4}\color{Cerulean}{a}\color{black}{+2}\color{OliveGreen}{b}\color{black}{+9}\color{OliveGreen}{b}&\color{Cerulean}{Commutative\:property\:of\:addition} \\ &=-1a+11b &\color{Cerulean}{Combine\:like\:terms.} \\ &=-a+11b \end{aligned}$

Respuesta:

$-a+11b$

En el ejemplo anterior, el reordenamiento de los términos se suele realizar mentalmente y no se muestra en la presentación de la solución.

Ejemplo$\PageIndex{7}$

Simplificar:

$x^{2}+3x+2+4x^{2}−5x−7$.

Solución:

Identificar los términos similares y sumar los coeficientes correspondientes.

$\begin{array}{lc}{\color{Cerulean}{\underline{1x^{2}}}\color{black}{+}\color{OliveGreen}{\underline{\underline{3x}}}\color{black}{+\underline{\underline{\underline{2}}}+}\color{Cerulean}{\underline{4x^{2}}}\color{black}{-}\color{OliveGreen}{\underline{\underline{5x}}}\color{black}{-\underline{\underline{\underline{7}}}}}&{\color{Cerulean}{Identify\:like\:terms.}}\\{=5x^{2}-2x-5}&{\color{Cerulean}{Combine\:like\:terms.}}\end{array}$

Respuesta:

$5x^{2}-2x-5$

Ejemplo$\PageIndex{8}$

Simplificar:

$5x^{2}y−3xy^{2}+4x^{2}y−2xy^{2}$.

Solución:

Recuerde dejar los factores variables y sus exponentes sin cambios en el término combinado resultante.

$\begin{array}{l}{\underline{5x^{2}y}-\underline{\underline{3xy^{2}}}+\underline{4x^{2}y}-\underline{\underline{2xy^{2}}}}\\{=9x^{2}y-5xy^{2}} \end{array}$

Respuesta:

$9x^{2}y-5xy^{2}$

Ejemplo$\PageIndex{9}$

Simplificar:

$\frac{1}{2}a−\frac{1}{3}b+\frac{3}{4}a+b$.

Para sumar los coeficientes fraccionarios, utilice coeficientes equivalentes con denominadores comunes para cada término similar.

$\begin{aligned} \frac{1}{2}a-\frac{1}{3}b+\frac{3}{4}a+1b&=\frac{1}{2}a+\frac{3}{4}a-\frac{1}{3}b+1b \\ &=\frac{2}{4}a+\frac{3}{4}a-\frac{1}{3}b+\frac{3}{3}b \\&=\frac{5}{4}a+\frac{2}{3}b \end{aligned}$

Respuesta:

$\frac{5}{4}a+\frac{2}{3}b$

Ejemplo$\PageIndex{10}$

Simplificar:

$−12x(x+y)^{3}+26x(x+y)^{3}$.

Solución:

Considera que la parte variable es$x(x+y)^{3}$. Entonces esta expresión tiene dos términos similares con coeficientes$−12$ y$26$.

$\begin{aligned} &-12x(x+y)^{3}+26x(x+y)^{3} &\color{Cerulean}{Add\:the\:coefficients.} \\ &=14x(x+y)^{3} \end{aligned}$

Respuesta:

$14x(x+y)^{3}$

Ejercicio$\PageIndex{2}$

Simplificar:

$−7x+8y−2x−3y$.

Contestar: $−9x+5y$

Propiedad distributiva y términos similares

Al simplificar, a menudo tendremos que combinar términos similares después de aplicar la propiedad distributiva. Este paso es consistente con el orden de las operaciones: multiplicación antes de la suma.

Ejemplo$\PageIndex{11}$

Simplificar:

$2(3a−b)$−$7(−2a+3b)$.

Solución:

Distribuir$2$$−7$ y luego combinar términos similares.

$Captura de pantalla (750) .png$

Figura$\PageIndex{2}$

Respuesta:

$20a-23b$

En el ejemplo anterior, es importante señalar que puedes eliminar los paréntesis y recolectar términos similares porque multiplicas la segunda cantidad por$−7$, no solo por$7$. Para aplicar correctamente la propiedad distributiva, piense en esto como sumar$−7$ veces la cantidad dada,$2(3a−b)+(−7)(−2a+3b)$.

Ejercicio$\PageIndex{3}$

Simplificar:

$−5(2x−3)+7x$.

Contestar: $-3x+15$

A menudo nos encontraremos con expresiones algebraicas como$+(a+b)$ o$−(a+b)$. Como hemos visto, los coeficientes en realidad están implícitos para ser$+1$ y$−1$, respectivamente, y por lo tanto, la propiedad distributiva se aplica usando$+1$ o$–1$ como factor. Multiplique cada término entre paréntesis por estos factores:

\[+(a+b)=+1(a+b)=(+1)a+(+1)b=a+b\]

\[-(a+b)=-1(a+b)=(-1)a+(-1)b=-a-b\]

Esto conduce a dos propiedades útiles,

\[+(a+b)=a+b\]

\[-(a+b)=-a-b\]

Ejemplo$\PageIndex{12}$

Simplificar:

$5x−(−2x^{2}+3x−1)$.

Solución:

Multiplique cada término dentro de los paréntesis por$−1$ y luego combine términos similares.

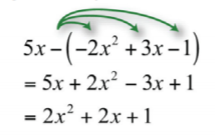$Captura de pantalla (751) .png$

Figura$\PageIndex{3}$

Respuesta:

$2x^{2}+2x+1$

Al distribuir un número negativo, todos los signos dentro de los paréntesis cambiarán. Obsérvese que$5x$ en el ejemplo anterior se encuentra un término separado; de ahí que la propiedad distributiva no le aplique.

Ejemplo$\PageIndex{13}$

Simplificar:

$5−2(x^{2}−4x−3)$.

Solución:

El orden de las operaciones requiere que nos multipliquemos antes de restar. Por lo tanto, distribuir$−2$ y luego combinar los términos constantes. Restar$5 − 2$ primero conduce a un resultado incorrecto, como se ilustra a continuación:

$\begin{array}{c|c}{\underline{\color{red}{Incorrect!}}}&{\underline{\color{Cerulean}{Correct!}}}\\{\begin{aligned} &\color{red}{5-2}\color{black}{(x^{2}-4x-3)} \\ &=\color{red}{3}\color{black}{(x^{2}-4x-3)}\\&=3x^{2}-12x-9\quad\color{red}{x} \end{aligned}}&{\begin{aligned}&5\color{Cerulean}{-2}\color{black}{(x^{2}-4x-3)} \\ &=5\color{Cerulean}{-2}\color{black}{x^{2}}\color{Cerulean}{+8}\color{black}{x}\color{Cerulean}{+6} \\ &=-2x^{2}+8x+11\quad\color{Cerulean}{\checkmark} \end{aligned}} \end{array}$

Respuesta:

$-2x^{2}+8x+11$

Nota

Vale la pena repetir que debes seguir el orden de las operaciones: ¡multiplicar y dividir antes de sumar y restar!

Ejercicio$\PageIndex{4}$

Simplificar:

$8−3(−x^{2}+2x−7)$.

Contestar: $3x^{2}-6x+29$

Ejemplo$\PageIndex{14}$

Restar$3x−2$ del doble de la cantidad$−4x^{2}+2x−8$.

Solución:

Primero, agrupa cada expresión y trata cada una como una cantidad:

$(3x-2)\qquad\text{and}\qquad (-4x^{2}+2x-8)$

A continuación, identificar las palabras clave y traducirlas en una expresión matemática.

$Captura de pantalla (752) .png$

Figura$\PageIndex{4}$

Por último, simplificar la expresión resultante.

Respuesta:

$-8x^{2}+x-14$

Claves para llevar

Las propiedades de los números reales se aplican a las expresiones algebraicas, porque las variables son simplemente representaciones de números reales desconocidos.
Combina términos similares, o términos con la misma parte variable, para simplificar expresiones.
Utilice la propiedad distributiva al multiplicar expresiones algebraicas agrupadas,$a(b+c)=ab+ac$.
Es una práctica recomendada aplicar la propiedad distributiva solo cuando la expresión dentro de la agrupación está completamente simplificada.
Después de aplicar la propiedad distributiva, elimine los paréntesis y luego combine cualquier término similar.
Siempre use el orden de las operaciones a la hora de simplificar.

Ejercicio$\PageIndex{5}$ Distributive Property

Multiplicar.

$3(3x−2)$
$12(−5y+1)$
$−2(x+1)$
$5(a−b)$
$\frac{5}{8}(8x−16)$
$−\frac{3}{5}(10x−5)$
$(2x+3)⋅2$
$(5x−1)⋅5$
$(−x+7)(−3)$
$(−8x+1)(−2)$
$−(2a−3b)$
$−(x−1)$
$\frac{1}{3}(2x+5)$
$−\frac{3}{4}(y−2)$
$−3(2a+5b−c)$
$−(2y^{2}−5y+7)$
$5(y^{2}−6y−9)$
$−6(5x^{2}+2x−1)$
$7x^{2}−(3x−11)$
$−(2a−3b)+c$
$3(7x^{2}−2x)−3$
$\frac{1}{2}(4a^{2}−6a+4)$
$−\frac{1}{3}(9y^{2}−3y+27)$
$(5x^{2}−7x+9)(−5)$
$6(\frac{1}{3}x^{2}−\frac{1}{6}x+\frac{1}{2})$
$−2(3x^{3}−2x^{2}+x−3)$
$\frac{20x+30y−10z}{10}$
$\frac{−4a+20b−8c}{4}$
$\frac{3x^{2}−9x+81}{−3}$
$\frac{15y^{2}+20y−5}{5}$

Contestar

1. $9x−6 $

3. $−2x−2 $

5. $5x−10 $

7. $4x+6 $

9. $3x−21 $

11. $−2a+3b$

13. $\frac{2}{3}x+\frac{5}{3}$

15. $−6a−15b+3c$

17. $5y^{2}−30y−45$

19. $7x^{2}−3x+11$

21. $21x^{2}−6x−3$

23. $−3y^{2}+y−9$

25. $2x^{2}−x+3$

27. $2x+3y−z$

29. $−x^{2}+3x−27$

Ejercicio$\PageIndex{6}$ Distributive Property

Traduzca las siguientes oraciones en expresiones algebraicas y luego simplifique.

Simplifica dos veces la expresión$25x^{2}−9$.
Simplifica lo contrario de la expresión$6x^{2}+5x−1$.
Simplificar el producto de$5$ y$x^{2}−8$.
Simplificar el producto de$−3$ y$−2x^{2}+x−8$.

Contestar

1. $50x^{2}−18$

3. $5x^{2}−40$

Ejercicio$\PageIndex{7}$ Combining Like Terms

Simplificar.

$2x−3x$
$−2a+5a−12a$
$10y−30−15y$
$\frac{1}{3}x+\frac{5}{12}x$
$−\frac{1}{4}x+\frac{4}{5}+\frac{3}{8}x$
$2x−4x+7x−x$
$−3y−2y+10y−4y$
$5x−7x+8y+2y$
$−8α+2β−5α−6β$
$−6α+7β−2α+β$
$3x+5−2y+7−5x+3y$
$–y+8x−3+14x+1−y$
$4xy−6+2xy+8$
$−12ab−3+4ab−20$
$\frac{1}{3}x−\frac{2}{5}y+\frac{2}{3}x−\frac{3}{5}y$
$\frac{3}{8}a−\frac{2}{7}b−\frac{1}{4}a+\frac{3}{14}b$
$−4x^{2}−3xy+7+4x^{2}−5xy−3$
$x^{2}+y^{2}−2xy−x^{2}+5xy−y^{2}$
$x^{2}−y^{2}+2x^{2}−3y$
$\frac{1}{2}x^{2}−\frac{2}{3}y^{2}−\frac{1}{8}x^{2}+\frac{1}{5}y^{2}$
$\frac{3}{16}a^{2}−\frac{4}{5}+\frac{1}{4}a^{2}−\frac{1}{4}$
$\frac{1}{5}y^{2}−\frac{3}{4}+\frac{7}{10}y^{2}−\frac{1}{2}$
$6x^{2}y−3xy^{2}+2x^{2}y−5xy^{2}$
$12x^{2}y^{2}+3xy−13x^{2}y^{2}+10xy$
$−ab^{2}+a^{2}b−2ab^{2}+5a^{2}b$
$m^{2}n^{2}−mn+mn−3m^{2}n+4m^{2}n^{2}$
$2(x+y)^{2}+3(x+y)^{2}$
$\frac{1}{5}(x+2)^{3}−\frac{2}{3}(x+2)^{3}$
$−3x(x^{2}−1)+5x(x^{2}−1)$
$5(x−3)−8(x−3)$
$−14(2x+7)+6(2x+7)$
$4xy(x+2)^{2}−9xy(x+2)^{2}+xy(x+2)^{2}$

Contestar

1. $−x$

3. $−5y−30$

5. $\frac{1}{8}x+\frac{4}{5}$

7. $y$

9. $−13α−4β$

11. $−2x+y+12$

13. $6xy+2$

15. $x−y$

17. $−8xy+4$

19. $3x^{2}−y^{2}−3y$

21. $\frac{7}{16}a^{2}−\frac{21}{20}$

23. $8x^{2}y−8xy^{2}$

25. $6a^{2}b−3ab^{2}$

27. $5(x+y)^{2}$

29. $2x(x^{2}−1)$

31. $−8(2x+7)$

Ejercicio$\PageIndex{8}$ Mixed Practice

Simplificar.

$5(2x−3)+7$
$−2(4y+2)−3y$
$5x−2(4x−5)$
$3−(2x+7)$
$2x−(3x−4y−1)$
$(10y−8)−(40x+20y−7)$
$\frac{1}{2}y−\frac{3}{4}x−(\frac{2}{3}y−\frac{1}{5}x)$
$\frac{1}{5}a−\frac{3}{4}b+\frac{3}{15}a−\frac{1}{2}b$
$\frac{2}{3}(x−y)+x−2y$
$−\frac{1}{3}(6x−1)+\frac{1}{2}(4y−1)−(−2x+2y−\frac{1}{6})$
$(2x^{2}−7x+1)+(x^{2}+7x−5)$
$6(−2x^{2}+3x−1)+10x^{2}−5x$
$−(x^{2}−3x+8)+x^{2}−12$
$2(3a−4b)+4(−2a+3b)$
$−7(10x−7y)−6(8x+4y)$
$10(6x−9)−(80x−35)$
$10−5(x^{2}−3x−1)$
$4+6(y^{2}−9)$
$\frac{3}{4}x−(\frac{1}{2}x^{2}+\frac{2}{3}x−\frac{7}{5})$
$−\frac{7}{3}x^{2}+(−\frac{1}{6}x^{2}+7x−1)$
$(2y^{2}−3y+1)−(5y^{2}+10y−7)$
$(−10a^{2}−b^{2}+c)+(12a^{2}+b^{2}−4c)$
$−4(2x^{2}+3x−2)+5(x^{2}−4x−1)$
$2(3x^{2}−7x+1)−3(x^{2}+5x−1)$
$x^{2}y+3xy^{2}−(2x^{2}y−xy^{2})$
$3(x^{2}y^{2}−12xy)−(7x^{2}y^{2}−20xy+18)$
$3−5(ab−3)+2(ba−4)$
$−9−2(xy+7)−(yx−1)$
$−5(4α−2β+1)+10(α−3β+2)$
$\frac{1}{2}(100α^{2}−50αβ+2β^{2})−\frac{1}{5}(50α^{2}+10αβ−5β^{2})$

Contestar

1. $10x−8$

3. $−3x+10$

5. $−x+4y+1$

7. $−\frac{11}{20}x−\frac{1}{6}y$

9. $\frac{5}{3}x−\frac{8}{3}y$

11. $3x^{2}−4$

13. $3x−20$

15. $−118x+25y$

17. $−5x^{2}+15x+15$

19. $−\frac{1}{2}x^{2}+\frac{1}{12}x+\frac{7}{5}$

21. $−3y^{2}−13y+8$

23. $−3x^{2}−32x+3$

25. $−x^{2}y+4xy^{2}$

27. $−3ab+10$

29. $−10α−20β+15$

Ejercicio$\PageIndex{9}$ Mixed Practice

Traduzca las siguientes oraciones en expresiones algebraicas y luego simplifique.

¿Cuál es la diferencia de$3x−4$ y$−2x+5$?
Restar$2x−3$ de$5x+7$.
Restar$4x+3$ del doble de la cantidad$x−2$.
Restar tres veces la cantidad$−x+8$ de$10x−9$.

Contestar

1. $5x-9$

3. $-2x-7$

Ejercicio$\PageIndex{10}$ Discussion Board Topics

¿Necesitamos una propiedad distributiva para división,$(a+b)÷c$? Explique.
¿Necesitamos una propiedad distributiva separada para tres términos,$a(b+c+d)$? Explique.
Explicar cómo restar una expresión de otra. Dar algunos ejemplos y demostrar la importancia del orden en que se realiza la resta.
Dada la expresión algebraica$8−5(3x+4)$, explicar por qué restar no$8−5$ es el primer paso.
¿Se puede aplicar la propiedad distributiva a la expresión$5(abc)$? Explica por qué o por qué no y da algunos ejemplos.
¿Cómo puedes verificar si has simplificado una expresión correctamente? Dar algunos ejemplos.

Contestar

1. Las respuestas pueden variar

3. Las respuestas pueden variar

5. Las respuestas pueden variar

Search

Text Color

Text Size

Margin Size

Font Type

Combinando términos similares

Propiedad distributiva y términos similares

Claves para llevar