1.4: Expresiones algebraicas y fórmulas

Última actualización
Guardar como PDF

Page ID: 109821

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Identificar las partes de una expresión algebraica.
Aplicar la propiedad distributiva.
Evaluar expresiones algebraicas.
Utilice fórmulas que modelen aplicaciones comunes.

Expresiones algebraicas y la propiedad distributiva

En álgebra se utilizan letras llamadas variables para representar números. Las combinaciones de variables y números junto con operaciones matemáticas forman expresiones algebraicas ⁸⁷, o solo expresiones. A continuación se presentan algunos ejemplos de expresiones con una variable,$x$:

Mesa$\PageIndex{1}$
$2x+3$	$x^{2}−9$	$\frac{1}{x}+\frac{x}{x+2}$	$3\sqrt{x}+x$

Los términos ⁸⁸ en una expresión algebraica están separados por operadores de suma y los factores ⁸⁹ están separados por operadores de multiplicación. El factor numérico de un término se llama el coeficiente ⁹⁰. Por ejemplo, la expresión algebraica$x^{2} y^{2} + 6xy − 3$ puede pensarse como$x^{2} y^{2} + 6xy + (−3)$ y tiene tres términos. El primer término,$x^{2} y^{2}$, representa la cantidad$1x^{2} y^{2} = 1 ⋅ x ⋅ x ⋅ y ⋅ y$ donde$1$ está el coeficiente y x e y son las variables. Todos los factores variables con sus exponentes forman la parte variable de un término ⁹¹. Si un término se escribe sin un factor variable, entonces se llama término constante ⁹². Considere los componentes de$x^{2} y^{2} + 6xy − 3$,

Mesa$\PageIndex{2}$
*Términos*	*Coeficiente*	*Parte Variable*
$x^{2}y^{2}$	$1$	$x^{2}y^{2}$
$6xy$	$6$	$xy$
$−3$	$−3$

El tercer término en esta expresión$−3$,, se denomina término constante porque está escrito sin un factor variable. Si bien una variable representa una cantidad desconocida y puede cambiar, el término constante no cambia.

Ejemplo$\PageIndex{1}$:

Enumerar todos los coeficientes y partes variables de cada término:$10a^{2}−5ab−b^{2}$.

Solución

Queremos pensar en el tercer término en este ejemplo$−b^{2}$ como$−1b^{2}$.

Mesa$\PageIndex{3}$
*Términos*	*Coeficiente*	*Parte Variable*
$10a^{2}$	$10$	$a^{2}$
$−5ab$	$−5$	$ab$
$−b^{2}$	$−1$	$b^{2}$

Respuesta: Coeficientes:$\{−5, −1, 10\}$; Partes variables:$\{a^{2}, ab, b^{2}\}$

En nuestro estudio del álgebra, encontraremos una amplia variedad de expresiones algebraicas. Normalmente, las expresiones utilizan las dos variables más comunes,$x$ y$y$. Sin embargo, las expresiones pueden usar cualquier letra (o símbolo) para una variable, incluso letras griegas, como alfa ($\alpha$) y beta ($\beta$). Algunas letras y símbolos están reservados para constantes, como$π ≈ 3.14159$ y$e ≈ 2.71828$. Dado que sólo hay un número limitado de letras, también se utilizarán subíndices,$x_{1} , x_{2} , x_{3} , x_{4} , …,$ para indicar diferentes variables.

Las propiedades de los números reales son importantes en nuestro estudio del álgebra porque una variable es simplemente una letra que representa un número real. En particular, el bien distributivo ⁹³ establece que si se le dan números reales$a, b$ y$c$, entonces,

$\color{Cerulean}{a}$$ ( b + c ) = \color{Cerulean}{a}$$b + \color{Cerulean}{a}$$c$

Esta propiedad es una que aplicamos a menudo a la hora de simplificar expresiones algebraicas. Para demostrar cómo se utilizará, simplificamos de dos$2(5 − 3)$ maneras, y observamos el mismo resultado correcto.

Mesa$\PageIndex{4}$
*Paréntesis de trabajo primero.*	*Uso de la propiedad distributiva.*
$ 2(\color{OliveGreen}{5−3}$$)=2(2)$ $=4$	$ 2(5−3)=$$\color{Cerulean}{2}$$⋅5−\color{Cerulean}{2}$$⋅3$ $=10−6$ $=4$

Ciertamente, si se puede simplificar el contenido de los paréntesis deberíamos hacerlo primero. Por otro lado, cuando los contenidos de los paréntesis no pueden simplificarse más, multiplicamos cada término dentro de él por el factor fuera de él utilizando la propiedad distributiva. Aplicar la propiedad distributiva nos permite multiplicar y eliminar los paréntesis.

Ejemplo$\PageIndex{2}$:

Simplificar:$5(−2a+5b)−2c$.

Solución

Multiplicar sólo los términos agrupados dentro de los paréntesis para los que estamos aplicando la propiedad distributiva.

$=\color{Cerulean}{5}$$⋅(−2a)+\color{Cerulean}{5}$$⋅5b−2c$

$=−10a+25b−2c$

Respuesta:$−10a+25b−2c$

Recordemos que la multiplicación es conmutativa y por lo tanto podemos escribir la propiedad distributiva de la siguiente manera,$(b + c) a = ba + ca$.

Ejemplo$\PageIndex{3}$:

Simplificar:$(3x−4y+1)⋅3$.

Solución

Multiplique todos los términos dentro del paréntesis por$3$.

$(3x−4y+1)⋅3=3x\color{Cerulean}{⋅3}$$−4y\color{Cerulean}{⋅3}$$+1\color{Cerulean}{⋅3}$

$=9x−12y+3$

Respuesta:$9x−12y+3$

Los términos cuyas partes variables tienen las mismas variables con los mismos exponentes se denominan términos similares ⁹⁴, o términos similares ⁹⁵. Además, los términos constantes se consideran como términos similares. Si una expresión algebraica contiene términos similares, aplique la propiedad distributiva de la siguiente manera:

$5 \color{Cerulean}{x}$$ + 7 \color{Cerulean}{x}$$ = ( 5 + 7 ) \color{Cerulean}{x}$$ = 12 \color{Cerulean}{x}$

$4 \color{Cerulean}{x ^ { 2 }}$$ + 5 \color{Cerulean}{x ^ { 2 }}$$ - 7 \color{Cerulean}{x ^ { 2 }}$$ = ( 4 + 5 - 7 ) \color{Cerulean}{x ^ { 2 }}$$ = 2 \color{Cerulean}{x ^ { 2 }}$

Es decir, si las partes variables de términos son exactamente las mismas, entonces podemos sumar o restar los coeficientes para obtener el coeficiente de un solo término con la misma parte variable. A este proceso se le llama combinar términos similares ⁹⁶. Por ejemplo,

$12 x ^ { 2 } y ^ { 3 } + 3 x ^ { 2 } y ^ { 3 } = 15 x ^ { 2 } y ^ { 3 }$

Observe que los factores variables y sus exponentes no cambian. Combinar términos similares de esta manera, para que la expresión no contenga otros términos similares, se llama simplificar la expresión ⁹⁷. Usa esta idea para simplificar expresiones algebraicas con múltiples términos similares.

Ejemplo$\PageIndex{4}$:

Simplificar:

$x ^ { 2 } - 10 x + 8 + 5 x ^ { 2 } - 6 x - 1$.

Solución

Identificar los términos similares y sumar los coeficientes correspondientes.

$\color{Cerulean}{\underline{1x^{2}}}$$ - \color{OliveGreen}{\underline{\underline{10x}}}$$ + \underline{\underline{\underline{8}}} + \color{Cerulean}{\underline{5 x ^ { 2 }}}$$ -\color{OliveGreen}{\underline{\underline{6x}}}$$ - \underline{\underline{\underline{1}}}$$\color{Cerulean}{Combine\: like\: terms.}$

$= 6 x ^ { 2 } - 16 x + 7$

Respuesta:$6 x ^ { 2 } - 16 x + 7$

Ejemplo$\PageIndex{5}$:

Simplificar:$a ^ { 2 } b ^ { 2 } - a b - 2 \left( 2 a ^ { 2 } b ^ { 2 } - 5 a b + 1 \right)$.

Solución

Distribuir$−2$ y luego combinar términos similares.

$\begin{aligned} a ^ { 2 } b ^ { 2 } - a b - 2 \left( 2 a ^ { 2 } b ^ { 2 } - 5 a b + 1 \right) & = a ^ { 2 } b ^ { 2 } - a b - 4 a ^ { 2 } b ^ { 2 } + 10 a b - 2 \\ & = - 3 a ^ { 2 } b ^ { 2 } + 9 a b - 2 \end{aligned}$

Respuesta:$- 3 a ^ { 2 } b ^ { 2 } + 9 a b - 2$

Evaluación de expresiones algebraicas

Una expresión algebraica se puede considerar como una generalización de operaciones aritméticas particulares. Realizar estas operaciones después de sustituir valores dados por variables se denomina evaluación ⁹⁸. En álgebra, una variable representa un valor desconocido. Sin embargo, si el problema asigna específicamente un valor a una variable, entonces puede reemplazar esa letra con el número dado y evaluar usando el orden de las operaciones.

Ejemplo$\PageIndex{6}$:

Evaluar:

$5x − 2$donde$x =\frac{2}{3}$
$y^{2} − y − 6$donde$y = −4$

Solución

Para evitar errores comunes, es una buena práctica reemplazar primero todas las variables por paréntesis, y luego reemplazar, o sustituir ⁹⁹, el valor dado apropiado.

$\begin{aligned} 5 x - 2 & = 5 (\:\: ) - 2 \\ & = 5 \left(\color{OliveGreen}{ \frac { 2 } { 3 }} \right) - 2 \\ & = \frac { 10 } { 3 } - \frac { 2 } { 1 } \cdot \color{Cerulean}{\frac { 3 } { 3 }} \\ & = \frac { 10 - 6 } { 3 } \\ & = \frac { 4 } { 3 } \end{aligned}$

$y ^ { 2 } - y - 6 = (\:\: ) ^ { 2 } - (\:\: ) - 6$

$= ( \color{OliveGreen}{- 4}$$ ) ^ { 2 } - ( \color{OliveGreen}{- 4}$$ ) - 6$

$\begin{array} { l } { = 16 + 4 - 6 } \\ { = 14 } \end{array}$

Respuesta:

a.$\frac{4}{3}$

b.$14$

A menudo, las expresiones algebraicas implicarán más de una variable.

Ejemplo$\PageIndex{7}$:

Evaluar$a ^ { 3 } - 8 b ^ { 3 }$ dónde$a = −1$ y$b = \frac{1}{2}$.

Solución

Después de sustituir en los valores apropiados, debemos tener cuidado de simplificar utilizando el orden correcto de las operaciones.

$a ^ { 3 } - 8 b ^ { 3 } = (\:\: ) ^ { 3 } - 8 (\:\: ) ^ { 3 } \color{Cerulean}{Replace\: variables\: with\: parentheses.}$

$= ( \color{OliveGreen}{- 1}$$ )^{3} -8(\color{OliveGreen}{\frac{1}{2}}$$)^{3} \color{Cerulean}{Substitute\: in\: the\: appropriate\: values.}$

$= - 1 - 8 \left( \frac { 1 } { 8 } \right) \color{Cerulean}{Simplify.}$

$\begin{array} { l } { = - 1 - 1 } \\ { = - 2 } \end{array}$

Respuesta:$-2$

Ejemplo$\PageIndex{8}$:

Evaluar$\frac { x ^ { 2 } - y ^ { 2 } } { 2 x - 1 }$ dónde$x = −\frac{3}{2}$ y$y = −3$.

Solución

$\frac { x ^ { 2 } - y ^ { 2 } } { 2 x - 1 } = \frac { (\:\: ) ^ { 2 } - ( \:\:) ^ { 2 } } { 2 ( \:\:) - 1 }$

$= \frac { \left( \color{OliveGreen}{- \frac { 3 } { 2 }} \right) ^ { 2 } - ( \color{OliveGreen}{- 3} \color{Black}{) ^ { 2 } }} { 2 \left( - \color{OliveGreen}{\frac { 3 } { 2 }} \right) - 1 }$

$= \frac { \frac { 9 } { 4 } - 9 } { - 3 - 1 }$

En este punto tenemos una fracción compleja. Simplifica el numerador y luego multiplica por el recíproco del denominador.

$\begin{aligned} & = \frac { \frac { 9 } { 4 } - \frac { 9 } { 1 } \cdot \color{Cerulean}{\frac { 4 } { 4 } }} { - 4 } \\ & = \frac { \frac { - 27 } { 4 } } { { \frac { - 4 } { 1 } } } \\ & = \frac { - 27 } { 4 } \left( - \frac { 1 } { 4 } \right) \\ & = \frac { 27 } { 16 } \end{aligned}$

Respuesta:$\frac { 27 } { 16 }$

La respuesta al ejemplo anterior se puede escribir como un número mixto,$\frac { 27 } { 16 } = 1 \frac { 11 } { 16 }$. A menos que el problema original tenga números mixtos en él, o sea una respuesta a una aplicación del mundo real, las soluciones se expresarán como fracciones impropias reducidas.

Ejemplo$\PageIndex{9}$:

Evaluar$\sqrt { b ^ { 2 } - 4 a c }$ dónde$a = −1, b = −7$, y$c = \frac{1}{4}$.

Solución

Sustituir en los valores apropiados y luego simplificar.

$\sqrt { b ^ { 2 } - 4 a c } = \sqrt { ( \:\: ) ^ { 2 } - 4 ( \:\: ) \:\:(\:\:) }$

$ = \sqrt { ( \color{OliveGreen}{- 7}\color{Black}{ ) ^ { 2 } - 4 (}\color{OliveGreen}{ - 1}\color{Black}{ ) (}\color{OliveGreen}{ \frac { 1 } { 4 }}\color{Black}{)} } $

$\begin{aligned} & =\sqrt { 49 + 4(\frac{1}{4}) } \\ & = \sqrt { 49 + 1 } \\ & =\sqrt{50} \\& = \sqrt { 25 \cdot 2 } \\ & = 5 \sqrt { 2 } \end{aligned}$

Alineados:$5 \sqrt { 2 }$

Ejercicio$\PageIndex{1}$

Evaluar$\frac { \sqrt { 3 \pi V h } } { \pi h }$ dónde$V = 25\pi$ y$h = 3$.

Contestar

$5$

www.youtube.com/v/y4rcmcethu4

Uso de fórmulas

La principal diferencia entre álgebra y aritmética es el uso organizado de variables. Esta idea lleva a fórmulas reutilizables ¹⁰⁰, que son modelos matemáticos que utilizan expresiones algebraicas para describir aplicaciones comunes. Por ejemplo, el volumen de un cono circular derecho depende de su radio$r$ y altura$h$ y está modelado por la fórmula:

$V = \frac { 1 } { 3 } \pi r ^ { 2 } h$

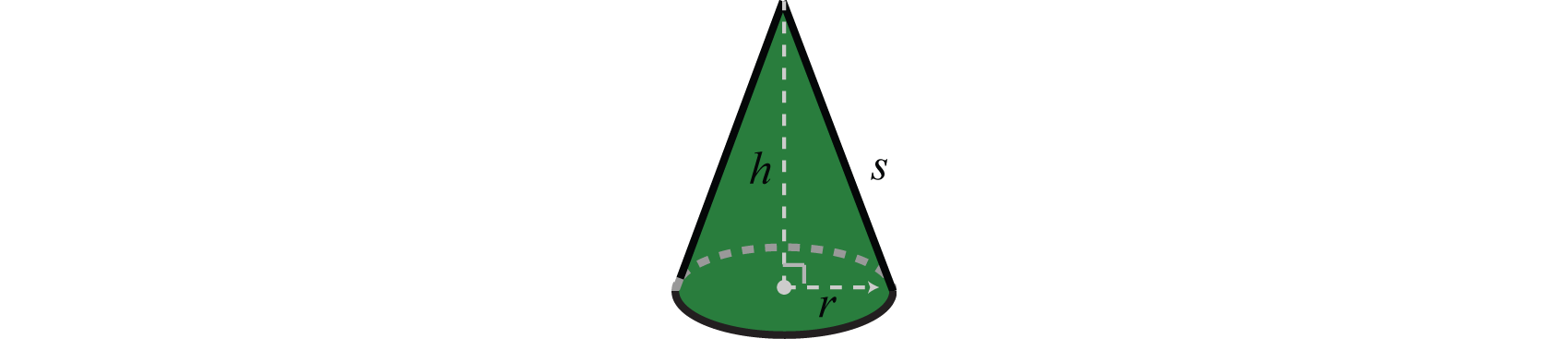
En esta ecuación se utilizan variables y constantes para describir la relación entre el volumen y la longitud de la base y la altura. Si el radio de la base mide$3$ metros y la altura mide$5$ metros, entonces el volumen se puede calcular usando la fórmula siguiente:

$\begin{aligned} V & = \frac { 1 } { 3 } \pi r ^ { 2 } h \\ & = \frac { 1 } { 3 } \pi ( 3 m ) ^ { 2 } ( 5 m ) \\ & = \frac { 1 } {\bcancel {3}} \pi \cdot \stackrel{\color{Cerulean}{3}}{\bcancel{9}} \cdot 5 m ^ { 3 } \\ & = 15 \pi \mathrm { m } ^ { 3 } \end{aligned}$

Utilizando$π ≈ 3.14$, podemos aproximar el volumen: metros$V ≈ 15 (3.14) = 47.1$ cúbicos.

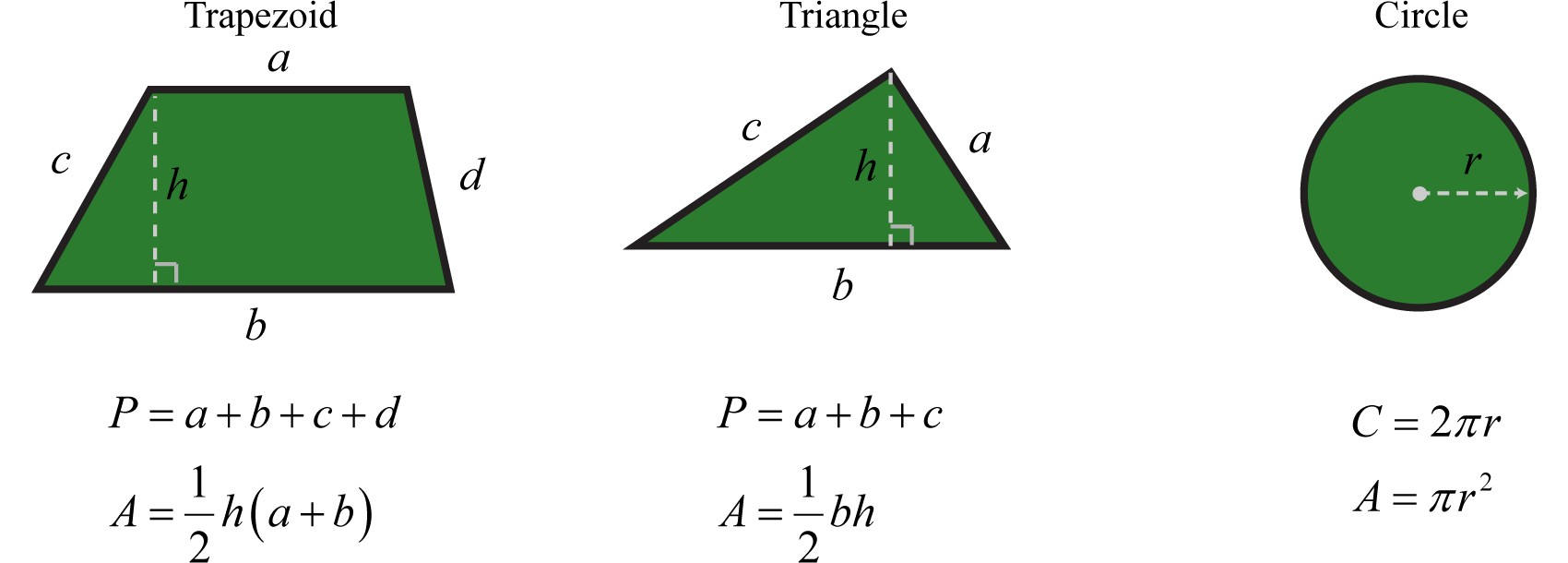
A continuación se presenta una lista de fórmulas que describen el área y el perímetro de las figuras del plano común. La letra P representa perímetro y se mide en unidades lineales. La letra A representa el área y se mide en unidades cuadradas.

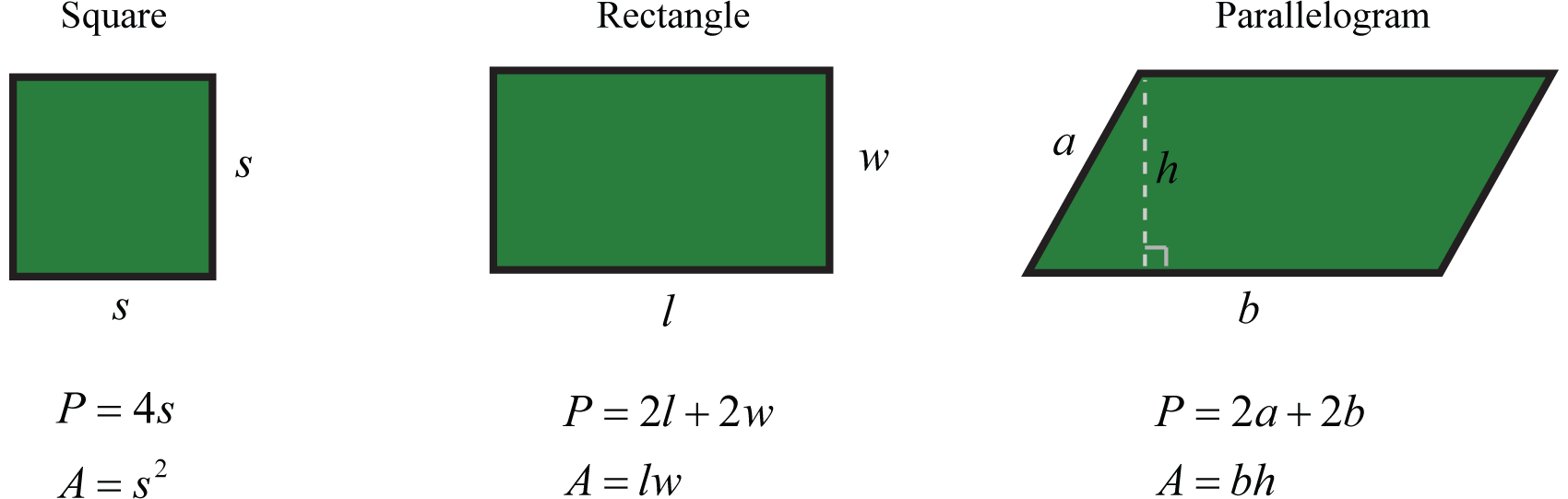
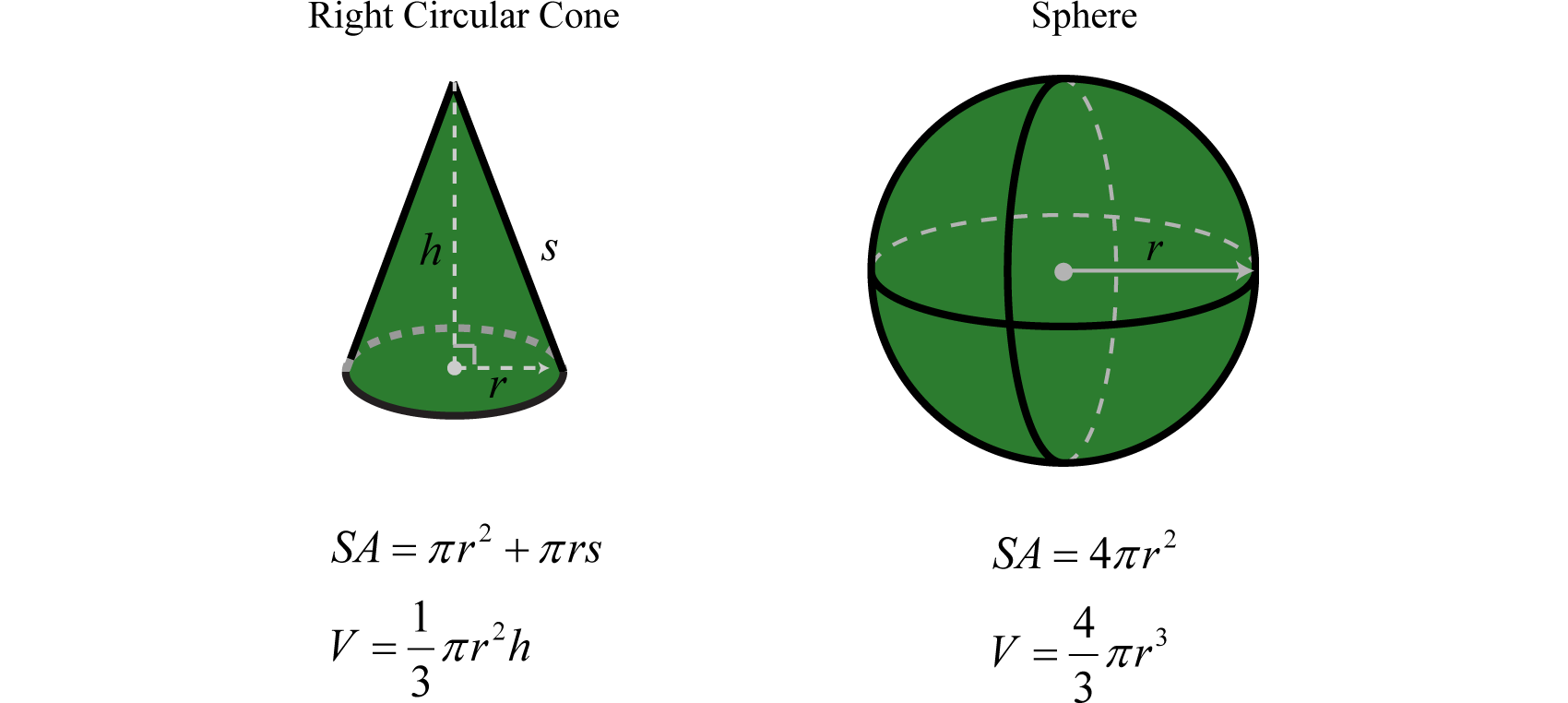
A continuación se presenta una lista de fórmulas que describen la superficie y el volumen de las figuras comunes. Aquí SA representa el área de superficie y se mide en unidades cuadradas. La letra V representa el volumen y se mide en unidades cúbicas.

Ejemplo$\PageIndex{10}$:

El diámetro de un globo esférico es de$10$ pulgadas. Determinar el volumen redondeado a la centésima más cercana.

Solución

La fórmula para el volumen de una esfera es

$V = \frac { 4 } { 3 } \pi r ^ { 3 }$

Esta fórmula da el volumen en términos del radio,$r$. Por lo tanto, divida el diámetro por$2$ y luego sumételo en la fórmula. Aquí,$r = \frac{10}{2} = 5$ pulgadas y tenemos

$\begin{aligned} V & = \frac { 4 } { 3 } \pi r ^ { 3 } \\ & = \frac { 4 } { 3 } \pi ( 5 \mathrm { in } ) ^ { 3 } \\ & = \frac { 4 } { 3 } \pi \cdot 125 \mathrm { in } ^ { 3 } \\ & = \frac { 500 \pi } { 3 } \mathrm { in } ^ { 3 } \approx 523.60 \mathrm { in } ^ { 3 } \end{aligned}$

Respuesta: El volumen del globo es de aproximadamente pulgadas$523.60$ cúbicas.

Las fórmulas se pueden encontrar en multitud de temas. Por ejemplo, el movimiento uniforme ¹⁰¹ es modelado por la fórmula$D = rt$, que expresa la distancia$D$, en términos de la tasa promedio, o velocidad,$r$ y el tiempo recorrido a ese ritmo,$t$. Esta fórmula,$D = rt$, se usa a menudo y se lee, “distancia equivale a tasa por tiempo”.

Ejemplo$\PageIndex{11}$:

El viaje por carretera de Jim tomó$2\:\frac{1}{2}$ horas a una velocidad promedio de$66$ millas por hora. ¿Hasta dónde viajó?

Solución

Sustituir los valores apropiados en la fórmula y luego simplificar.

$\begin{aligned} D & = r \cdot t \\ & = ( \color{Cerulean}{66 \frac { \mathrm { mi } } { \mathrm { hr } }}\color{Black}{ ) \cdot (}\color{Cerulean}{ 2 \frac { 1 } { 2 } \mathrm { hr }}\color{Black}{)} \\ & = \frac { 66 } { 1 } \cdot \frac { 5 } { 2 } \mathrm { mi } \\ & = 33 \cdot 5 \mathrm { mi } \\ & = 165 \mathrm { mi } \end{aligned}$

Respuesta: Jim viajó$165$ millas.

El interés simple ¹⁰²$I$ viene dado por la fórmula$I = prt$, donde$p$ representa el monto principal invertido a una tasa de interés anual$r$ por$t$ años.

Ejemplo$\PageIndex{12}$:

Calcular los intereses simples devengados por una inversión$2$ -año de$$1,250$ a una tasa de interés anual de$3\:\frac{3}{4} %$.

Solución

Convertir$3\:\frac{3}{4}%$ a un número decimal antes de usarlo en la fórmula.

$r = 3 \frac { 3 } { 4 } \% = 3.75 \% = 0.0375$

Utilice esto y el hecho de que$p = $1,250$ y$t = 2$ años para calcular el interés simple.

$\begin{aligned} I & = p r t \\ & = ( \color{Cerulean}{1,250}\color{Black}{ ) (}\color{Cerulean}{ 0.0375}\color{Black}{ ) (}\color{Cerulean}{ 2}\color{Black}{ )} \\ & = 93.75 \end{aligned}$

Respuesta: El simple interés ganado es$$93.75$.

Claves para llevar

Piense en las expresiones algebraicas como generalizaciones de operaciones aritméticas comunes que se forman combinando números, variables y operaciones matemáticas.
La propiedad distributiva$a (b + c) = ab + ac$, se utiliza al multiplicar expresiones algebraicas agrupadas. Aplicar la propiedad distributiva nos permite eliminar paréntesis.
Combinar términos similares, o términos cuyas partes variables tengan las mismas variables con los mismos exponentes, sumando o restando los coeficientes para obtener el coeficiente de un solo término con la misma parte variable. Recuerde que los factores variables y sus exponentes no cambian.
Para evitar errores comunes a la hora de evaluar, es una buena práctica reemplazar todas las variables por paréntesis y luego sustituir los valores apropiados.
El uso de expresiones algebraicas nos permite crear fórmulas útiles y reutilizables que modelan aplicaciones comunes.

Ejercicio$\PageIndex{2}$

Enumere todos los coeficientes y partes variables de cada término.

$−5x^{2} + x − 1$
$y^{2} − 9y + 3$
$5x^{2} − 3xy + y^{2}$
$a^{2}b^{2} + 2ab − 4$
$x^{2}y + xy^{2} − 3xy + 9$
$x^{4} − x^{3} + x^{2} − x + 2$

Contestar

1. Coeficientes:$\{−5, 1, −1\}$; partes variables:$\{x^{2} , x\}$

3. Coeficientes:$\{5, −3, 1\}$; partes variables:$\{x^{2} , xy, y^{2} \}$

5. Coeficientes:$\{1, −3, 9\}$; partes variables:$\{x^{2}y, xy^{2} , xy\}$

Ejercicio$\PageIndex{3}$

Multiplicar.

$5 (3x − 5) $
$3 (4x − 1) $
$−2 (2x^{2} − 5x + 1) $
$−5 (6x^{2} − 3x − 1)$
$\frac{2}{3} (9y^{2} + 12y − 3)$
$−\frac{3}{4} (8y^{2} + 20y + 4)$
$12(\frac{1}{3} a^{2} − \frac{5}{6} a + \frac{7}{12} )$
$−9 (\frac{1}{9} a^{2} − \frac{5}{3} a + 1 )$
$9 (a^{2} − 2b^{2} )$
$−5 (3x^{2} − y^{2} )$
$(5a^{2} − 3ab + b^{2} ) ⋅ 6$
$(a^{2}b^{2} − 9ab − 3) ⋅ 7$
$− (5x^{2} − xy + y^{2} )$
$− (x^{2}y^{2} − 6xy − 1)$

Contestar

1. $15x − 25$

3. $−4x^{2} + 10x − 2$

5. $6y^{2} + 8y − 2$

7. $4a^{2} − 10a + 7$

9. $9a^{2} − 18b^{2}$

11. $30a^{2} − 18ab + 6b^{2}$

13. $−5x^{2} + xy − y^{2}$

Ejercicio$\PageIndex{4}$

Combina términos similares.

$18x − 5x + 3x$
$30x − 50x + 10x$
$3y − 4 + 2y − 12$
$12y + 7 − 15y − 6$
$2x^{2} − 3x + 2 + 5x^{2} − 6x + 1$
$9x^{2} + 7x − 5 − 10x^{2} − 8x + 6$
$\frac{3}{5} a^{2} − \frac{1}{2} + \frac{1}{3} a^{2} + \frac{4}{5}$
$\frac{1}{6} a^{2} + \frac{2}{3} − \frac{4}{3} a^{2} − \frac{1}{9}$
$\frac{1}{2} y^{2} + \frac{2}{3} y − 3 + \frac{3}{5} y^{2} + \frac{1}{3} y − \frac{7}{3}$
$\frac{5}{6} x^{2} + \frac{1}{8} x − 1 − \frac{1}{2} x^{2} + \frac{3}{4} x − \frac{4}{5}$
$a^{2}b^{2} + 5ab − 2 + 7a^{2}b^{2} − 6ab + 12$
$a^{2} − 12ab + 4b^{2} − 6a^{2} + 10ab − 5b^{2}$
$3x^{2}y + 12xy − 5xy^{2} + 5xy − 8x^{2}y + 2xy^{2}$
$10x^{2}y + 2xy − 4xy^{2} + 2x^{2}y − 8xy + 5xy^{2}$
$7m^{2}n − 9mn + mn^{2} − 6m^{2}n + mn − 2mn^{2}$
$m^{2}n − 5mn + 5mn^{2} − 3m^{2}n + 5mn + 2mn^{2}$
$x^{2n} − 3x^{n} + 5 + 2x^{2n} − 4x^{n} − 3$
$5y^{2n} − 3y^{n} + 1 − 3y^{2n} − 2y^{n} − 1$

Contestar

1. $16x$

3. $5y − 16$

5. $7x^{2} − 9x + 3$

7. $\frac{14}{15}a^{2} + \frac{3}{10}$

9. $\frac{11}{10} y^{2} + y − \frac{16}{3}$

11. $8a^{2}b^{2} − ab + 10$

13. $−5x^{2}y + 17xy − 3xy^{2}$

15. $m^{2}n − 8mn − mn^{2}$

17. $3x^{2n} − 7x^{n} + 2$

Ejercicio$\PageIndex{5}$

Simplificar.

$5 − 2 (4x + 8)$
$8 − 6 (2x − 1)$
$2 (x^{2} − 7x + 1) + 3x − 7$
$−5 (x^{2} + 4x − 1) + 8x^{2} − 5$
$5ab − 4 (ab + 5)$
$5 (7 − ab) + 2ab$
$2 − a^{2} + 3 (a^{2} + 4)$
$7 − 3y + 2 (y^{2} − 3y − 2)$
$8x^{2} − 3x − 5 (x^{2} + 4x − 1)$
$2 − 5y − 6 (y^{2} − y + 2)$
$a^{2}b^{2} − 5 + 3 (a^{2}b^{2} − 3ab + 2)$
$a^{2} − 3ab − 2 (a^{2} − ab + 1)$
$10y^{2} + 6 − (3y^{2} + 2y + 4)$
$4m^{2} − 3mn − (m^{2} − 3mn + n^{2} )$
$x^{2n} − 3x^{n} + 5 (x^{2n} − x^{n} + 1)$
$−3 (y^{2n} − 2y^{n} + 1) + 4y^{2n} − 5$

Contestar

1. $−8x − 11$

3. $2x^{2} − 11x − 5$

5. $ab − 20$

7. $2a^{2} + 14$

9. $3x^{2} − 23x + 5$

11. $4a^{2}b^{2} − 9ab + 1$

13. $7y^{2} − 2y + 2$

15. $6x^{2n} − 8x^{n} + 5$

Ejercicio$\PageIndex{6}$

Evaluar.

$−2x + 3$donde$x = −2$
$8x − 5$donde$x = −1$
$x^{2} − x + 5$donde$x = −5$
$2x^{2} − 8x + 1$donde$x = 3$
$\frac { x ^ { 2 } - x + 2 } { 2 x - 1 }$donde$x = -\frac{1}{2}$
$\frac { 9 x ^ { 2 } + x - 2 } { 3 x - 4 }$donde$x = -\frac{2}{3}$
$( 3 y - 2 ) ( y + 5 )$donde$y = \frac { 2 } { 3 }$
$(3x + 2) (5x + 1)$donde$x = −\frac{1}{5}$
$(3x − 1) (x − 8)$donde$x = −1$
$(7y + 5) (y + 1)$donde$y = −2$
$y^{6} − y^{3} + 2$donde$y = −1$
$y^{5} + y^{3} − 3$donde$y = −2$
$a^{2} − 5b^{2}$dónde$a = −2$ y$b = −1$
$a^{3} − 2b^{3}$dónde$a = −3$ y$b = 2$
$(x − 2y) (x + 2y)$dónde$x = 2$ y$y = −5$
$(4x − 3y) (x − y)$dónde$x = −4$ y$y = −3$
$a^{2} − ab + b^{2}$dónde$a = −1$ y$b = −2$
$x^{2}y^{2} − xy + 2$dónde$x = −3$ y$y = −2$
$a^{4} − b^{4}$dónde$a = −2$ y$b = −3$
$a^{6} − 2a^{3}b^{3} − b^{6}$dónde$a = 2$ y$b = −1$

Contestar

1. $7$

3. $35$

5. $−\frac{11}{8}$

7. $0$

9. $36$

11. $4$

13. $−1$

15. $−96$

17. $3$

19. $−65$

Ejercicio$\PageIndex{7}$

Evaluar$\sqrt { b ^ { 2 } - 4 a c }$ dados los siguientes valores.

$a = 6, b = 1$y$c = −1$
$a = 15, b = 4$y$c = −4$
$a = \frac{3}{4} , b = −2$y$c = −4$
$a = \frac{1}{2} , b = −2$y$c = −30$
$a = 1, b = 2$y$c = −1$
$a = 1, b = −4$y$c = −50$
$a = 1, b = −1$y$c = −\frac{1}{16}$
$a = −2, b = −\frac{1}{3}$y$c = 1$

Contestar

1. $5$

3. $4$

5. $2\sqrt{2}$

7. $\frac { \sqrt { 5 } } { 2 }$

Ejercicio$\PageIndex{8}$

Convertir las siguientes temperaturas a grados Celsius dadas$C = \frac{5}{9} (F − 32)$, donde F representa grados Fahrenheit.

$95°$F
$86°$F
$32°$F
$−40°$F

Contestar

1. $35°$C

3. $0°$C

Ejercicio$\PageIndex{9}$

Calcular el perímetro y el área de un rectángulo con dimensiones$12$ pies a$5$ pies.
Calcular el perímetro y el área de un rectángulo con dimensiones$5$ metros por$1$ metro.
Calcular el área de superficie y el volumen de una esfera con$6$ centímetros de radio.
El radio de la base de un cilindro circular derecho mide$4$ pulgadas y la altura mide$10$ pulgadas. Calcular la superficie y el volumen.
Calcular el volumen de una esfera con un diámetro de$18$ centímetros.
El diámetro de la base de un cono circular derecho mide$6$ pulgadas. Si la altura es$1\:\frac{1}{2}$ pies, entonces calcula su volumen.
Dado que la altura de un cilindro circular derecho es igual al radio de la base, derivar una fórmula para el área de superficie en términos del radio de la base.
Dado que el área de la base de un cilindro circular derecho es de pulgadas$25π$ cuadradas, encuentra el volumen si la altura es$1$ pie.
José pudo conducir de Tucson a Phoenix en$2$ horas a una velocidad promedio de$58$ mph. ¿A cuánta distancia está Phoenix de Tucson?
Si un tren bala puede promediar$152$ mph, entonces ¿hasta dónde puede viajar en$\frac{3}{4}$ una hora?
Margaret viajó por$1\:\frac{3}{4}$ hora a una velocidad promedio de$68$ millas por hora. ¿Hasta dónde viajó?
El viaje de Flagstaff, AZ al parque nacional del Gran Cañón tomó$1\:\frac{1}{2}$ horas a una velocidad promedio de$54$ mph. ¿A qué distancia está el parque nacional del Gran Cañón de Flagstaff?
Calcular los intereses simples devengados por una inversión$3$ -año de$$2,500$ a una tasa de interés anual de$5\:\frac{1}{4} $%.
Calcular los intereses simples devengados por una inversión$1$ -año de$$5,750$ a una tasa de interés anual de$2\:\frac{5}{8} $%.
¿Cuál es el interés simple que se gana en una inversión$5$ -año de$$20,000$ a una tasa de interés anual de$6$%?
¿Cuál es el interés simple que se gana en una inversión$1$ -año de$$50,000$ a una tasa de interés anual de$4.5$%?
El tiempo$t$ en segundos que un objeto está en caída libre viene dado por la fórmula$t = \frac { \sqrt { s } } { 4 }$, donde s representa la distancia en pies que ha caído el objeto. ¿Cuánto tiempo tarda un objeto en caer$32$ pies? (Dar la respuesta exacta y la respuesta aproximada a la centésima más cercana.)
La corriente$I$ medida en amperios, viene dada por la fórmula$I = \sqrt { \frac { P } { R } }$, donde$P$ se mide el consumo de energía en vatios, y$R$ es la resistencia medida en ohmios. Si una bombilla utiliza$60$ vatios de potencia y tiene$240$ ohmios de resistencia, entonces ¿cuántos amperios de corriente se requieren?

Contestar

1. $P = 34$pies$A = 60$ cuadrados; pies cuadrados

3. $SA = 144π$centímetros cuadrados; centímetros$V = 288π$ cúbicos

5. $972π$centímetros cúbicos

7. $SA = 4πr^{2}$

9. $116$millas

11. $119$millas

13. $$393.75$

15. $$6,000$

17. $\sqrt { 2 } \approx 1.41$segundos

Ejercicio$\PageIndex{10}$

Encuentra y publica un modelo matemático útil. Demostrar su uso con algunos valores.
Investigar y discutir la historia de la variable. ¿Qué podemos usar si nos quedamos sin letras?
Encuentre y publique un enlace a un recurso útil que describa el alfabeto griego.
Dada la expresión algebraica$5 − 3 (9x − 1)$, explicar por qué no restamos$5$ y$3$ primero.
¿Necesitamos una propiedad distributiva separada por más de dos términos? Por ejemplo,$a (b + c + d) = ab + ac + ad$. Explique.
¿Cómo podemos verificar para ver si hemos simplificado una expresión correctamente?

Contestar

1. La respuesta puede variar

3. La respuesta puede variar

5. La respuesta puede variar

Notas al pie

⁸⁷ Combinaciones de variables y números junto con operaciones matemáticas utilizadas para generalizar operaciones aritméticas específicas.

⁸⁸ Componentes de una expresión algebraica separados por operadores de adición.

⁸⁹ Componentes de un término separados por operadores de multiplicación.

⁹⁰ El factor numérico de un término.

⁹¹ Todos los factores variables con sus exponentes.

⁹² Término escrito sin factor variable.

⁹³ Dado cualquier número$a, b,$ real$c, a (b + c) = ab + ac$ y/o$(b + c) a = ba + ca$.

⁹⁴ Términos o términos constantes cuyas partes variables tienen las mismas variables con los mismos exponentes.

⁹⁵ Se utiliza cuando se refiere a términos similares.

⁹⁶ Sumar o restar términos similares dentro de una expresión algebraica para obtener un solo término con la misma parte variable.

⁹⁷ El proceso de combinar términos similares hasta que la expresión no contenga más términos similares.

⁹⁸ El proceso de realizar las operaciones de una expresión algebraica para valores dados de las variables.

⁹⁹ El acto de sustituir una variable por una cantidad equivalente.

¹⁰⁰ Un modelo matemático reutilizable que utiliza expresiones algebraicas para describir una aplicación común.

¹⁰¹ La distancia$D$ después de viajar a una tasa promedio$r$ por algún tiempo se$t$ puede calcular usando la fórmula$D = rt$.

¹⁰² Modelado por la fórmula$I = prt$, donde$p$ representa el monto principal invertido a una tasa de interés anual$r$ por$t$ años.

*Términos*	*Coeficiente*	*Parte Variable*
\(x^{2}y^{2}\)	\(1\)	\(x^{2}y^{2}\)
\(6xy\)	\(6\)	\(xy\)
\(−3\)	\(−3\)

*Términos*	*Coeficiente*	*Parte Variable*
\(10a^{2}\)	\(10\)	\(a^{2}\)
\(−5ab\)	\(−5\)	\(ab\)
\(−b^{2}\)	\(−1\)	\(b^{2}\)

Search

Text Color

Text Size

Margin Size

Font Type