1.E: Fundamentos de álgebra (Ejercicios)

Última actualización
Guardar como PDF

Page ID: 109798

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ejercicio$\PageIndex{1}$

Reducir a los términos más bajos.

$\frac{56}{120}$
$\frac{54}{60}$
$\frac{155}{90}$
$\frac{315}{120}$

Contestar

1. $\frac{7}{15}$

3. $\frac{31}{18}$

Ejercicio$\PageIndex{2}$

Simplificar.

$- \left( - \frac { 1 } { 2 } \right)$
$- \left( - \left( - \frac { 5 } { 8 } \right) \right)$
$- ( - ( - a ) )$
$- ( - ( - ( - a ) ) )$

Contestar

1. $\frac{1}{2}$

3. $-a$

Ejercicio$\PageIndex{3}$

Grafique el conjunto de soluciones y dé la notación de intervalo equivalente.

$x \geq - 10$
$x < 0$
$- 8 \leq x < 0$
$- 10 < x \leq 4$
$x < 3 \text { and } x \geq - 1$
$x < 0 \text { and } x > 1$
$x < - 2 \text { or } x > - 6$
$x \leq - 1 \text { or } x > 3$

Contestar

1. $[ - 10 , \infty )$;

Figura 1.E.1

3. $[ - 8,0 )$;

Figura 1.E.2

5. $[ - 1,3 )$;

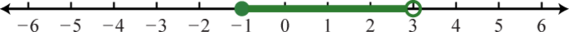
Figura 1.E.3

7. $\mathbb { R }$

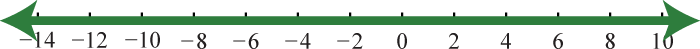
Figura 1.E.4

Ejercicio$\PageIndex{4}$

Determinar la desigualdad que corresponde al conjunto expresado mediante notación de intervalos.

$[ - 8 , \infty )$
$( - \infty , - 7 )$
$[ 12,32 ]$
$[ - 10,0 )$
$( - \infty , 1 ] \cup ( 5 , \infty )$
$( - \infty , - 10 ) \cup ( - 5 , \infty )$
$( - 4 , \infty )$
$( - \infty , 0 )$

Contestar

1. $x \geq - 8$

3. $12 \leq x \leq 32$

5. $x \leq 1 \text { or } x > 5$

7. $x > - 4$

Ejercicio$\PageIndex{5}$

Simplificar.

$- \left| - \frac { 3 } { 4 } \right|$
$- \left| - \left( - \frac { 2 } { 3 } \right) \right|$
$- ( - | - 4 | )$
$- ( - ( - | - 3 | ) )$

Contestar

1. $-\frac{3}{4}$

3. $4$

Ejercicio$\PageIndex{6}$

Determinar los valores representados por$a$.

$| a | = 6$
$| a | = 1$
$| a | = - 5$
$| a | = a$

Contestar

1. $a = \pm 6$

2. $\varnothing$

Ejercicio$\PageIndex{7}$

Realizar las operaciones.

$\frac { 1 } { 4 } - \frac { 1 } { 5 } + \frac { 3 } { 20 }$
$\frac { 2 } { 3 } - \left( - \frac { 3 } { 4 } \right) - \frac { 5 } { 12 }$
$\frac { 5 } { 3 } \left( - \frac { 6 } { 7 } \right) \div \left( \frac { 5 } { 14 } \right)$
$\left( - \frac { 8 } { 9 } \right) \div \frac { 16 } { 27 } \left( \frac { 2 } { 15 } \right)$
$\left( - \frac { 2 } { 3 } \right) ^ { 3 }$
$\left( - \frac { 3 } { 4 } \right) ^ { 2 }$
$( - 7 ) ^ { 2 } - 8 ^ { 2 }$
$- 4 ^ { 2 } + ( - 4 ) ^ { 3 }$
$10 - 8 \left( ( 3 - 5 ) ^ { 2 } - 2 \right)$
$4 + 5 \left( 3 - ( 2 - 3 ) ^ { 2 } \right)$
$- 3 ^ { 2 } - \left( 7 - ( - 4 + 2 ) ^ { 3 } \right)$
$( - 4 + 1 ) ^ { 2 } - ( 3 - 6 ) ^ { 3 }$
$\frac { 10 - 3 ( - 2 ) ^ { 3 } } { 3 ^ { 2 } - ( - 4 ) ^ { 2 } }$
$\frac { 6 \left[ ( - 5 ) ^ { 2 } - ( - 3 ) ^ { 2 } \right] } { 4 - 6 ( - 2 ) ^ { 2 } }$
$7 - 3 \left| 6 - ( - 3 - 2 ) ^ { 2 } \right|$
$- 6 ^ { 2 } + 5 \left| 3 - 2 ( - 2 ) ^ { 2 } \right|$
$\frac { 12 - \left| 6 - 2 ( - 4 ) ^ { 2 } \right| } { 3 - | - 4 | }$
$\frac { - ( 5 - 2 | - 3 | ) ^ { 3 } } { \left| 4 - ( - 3 ) ^ { 2 } \right| - 3 ^ { 2 } }$

Contestar

1. $\frac{1}{5}$

3. $-4$

5. $-\frac{8}{27}$

7. $-15$

9. $-6$

11. $-24$

13. $-\frac{34}{7}$

15. $-50$

17. $14$

Ejercicio$\PageIndex{8}$

Simplificar.

$3 \sqrt { 8 }$
$5 \sqrt { 18 }$
$6 \sqrt { 0 }$
$\sqrt { - 6 }$
$\sqrt { \frac { 75 } { 16 } }$
$\sqrt { \frac { 80 } { 49 } }$
$\sqrt [ 3 ] { 40 }$
$\sqrt [ 3 ] { 81 }$
$\sqrt [ 3 ] { - 81 }$
$\sqrt [ 3 ] { - 32 }$
$\sqrt [ 3 ] { \frac { 250 } { 27 } }$
$\sqrt [ 3 ] { \frac { 1 } { 125 } }$

Contestar

1. $6 \sqrt { 2 }$

3. $0$

5. $\frac { 5 \sqrt { 3 } } { 4 }$

7. $2 \sqrt [ 3 ] { 5 }$

9. $- 3 \sqrt [ 3 ] { 3 }$

11. $\frac { 5 \sqrt [ 3 ] { 2 } } { 3 }$

Ejercicio$\PageIndex{9}$

Use una calculadora para aproximar lo siguiente a la milésima más cercana.

$\sqrt { 12 }$
$3 \sqrt { 14 }$
$\sqrt [ 3 ] { 18 }$
$7 \sqrt [ 3 ] { 25 }$
Encuentra la longitud de la diagonal de un cuadrado con lados que miden$8$ centímetros.
Encuentra la longitud de la diagonal de un rectángulo con lados que miden$6$ centímetros y$12$ centímetros.

Contestar

1. $3.464$

3. $2.621$

5. $8 \sqrt { 2 }$centímetros

Ejercicio$\PageIndex{10}$

Multiplicar

$\frac { 2 } { 3 } \left( 9 x ^ { 2 } + 3 x - 6 \right)$
$- 5 \left( \frac { 1 } { 5 } y ^ { 2 } - \frac { 3 } { 5 } y + \frac { 1 } { 2 } \right)$
$\left( a ^ { 2 } - 5 a b - 2 b ^ { 2 } \right) ( - 3 )$
$\left( 2 m ^ { 2 } - 3 m n + n ^ { 2 } \right) \cdot 6$

Contestar

1. $6 x ^ { 2 } + 2 x - 4$

3. $- 3 a ^ { 2 } + 15 a b + 6 b ^ { 2 }$

Ejercicio$\PageIndex{11}$

Combina términos similares.

$5 x ^ { 2 } y - 3 x y ^ { 2 } - 4 x ^ { 2 } y - 7 x y ^ { 2 }$
$9 x ^ { 2 } y ^ { 2 } + 8 x y + 3 - 5 x ^ { 2 } y ^ { 2 } - 8 x y - 2$
$a ^ { 2 } b ^ { 2 } - 7 a b + 6 - a ^ { 2 } b ^ { 2 } + 12 a b - 5$
$5 m ^ { 2 } n - 3 m n + 2 m n ^ { 2 } - 2 n m - 4 m ^ { 2 } n + m n ^ { 2 }$

Contestar

1. $x ^ { 2 } y - 10 x y ^ { 2 }$

3. $5 a b + 1$

Ejercicio$\PageIndex{12}$

Simplificar.

$5 x ^ { 2 } + 4 x - 3 \left( 2 x ^ { 2 } - 4 x - 1 \right)$
$\left( 6 x ^ { 2 } y ^ { 2 } + 3 x y - 1 \right) - \left( 7 x ^ { 2 } y ^ { 2 } - 3 x y + 2 \right)$
$a ^ { 2 } - b ^ { 2 } - \left( 2 a ^ { 2 } + a b - 3 b ^ { 2 } \right)$
$m ^ { 2 } + m n - 6 \left( m ^ { 2 } - 3 n ^ { 2 } \right)$

Contestar

1. $- x ^ { 2 } + 16 x + 3$

3. $- a ^ { 2 } - a b + 2 b ^ { 2 }$

Ejercicio$\PageIndex{13}$

Evaluar.

$x ^ { 2 } - 3 x + 1 \text { where } x = - \frac { 1 } { 2 }$
$x ^ { 2 } - x - 1 \text { where } x = - \frac { 2 } { 3 }$
$a ^ { 4 } - b ^ { 4 } \text { where } a = - 3 \text { and } b = - 1$
$a ^ { 2 } - 3 a b + 5 b ^ { 2 } \text { where } a = 4 \text { and } b = - 2$
$( 2 x + 1 ) ( x - 3 ) \text { where } x = - 3$
$( 3 x + 1 ) ( x + 5 ) \text { where } x = - 5$
$\sqrt { b ^ { 2 } - 4 a c } \text { where } a = 2 , b = - 4 , \text { and } c = - 1$
$\sqrt { b ^ { 2 } - 4 a c } \text { where } a = 3 , b = - 6 , \text { and } c = - 2$
$\pi r ^ { 2 } h \text { where } r = 2 \sqrt { 3 } \text { and } h = 5$
$\frac { 4 } { 3 } \pi r ^ { 3 } \text { where } r = 2 \sqrt [ 3 ] { 6 }$
¿Cuál es el interés simple que se gana en una inversión$4$ anual de$$4,500$ a una tasa de interés anual de$4 \frac{3}{4}$%?
James viajó a una velocidad promedio de$48$ millas por hora durante$2 \frac{1}{4}$ horas. ¿Qué tan lejos viajó?
El periodo de un péndulo$T$ en segundos viene dado por la fórmula$T = 2 \pi \sqrt { \frac { L } { 32 } }$ donde$L$ representa su longitud en pies. Aproximar el periodo de un péndulo con longitud$2$ pies. Redondear a la décima de pie más cercana.
La distancia promedio$d$, en millas, una persona puede ver un objeto viene dada por la fórmula$d = \frac { \sqrt { 6 h } } { 2 }$ donde$h$ representa la altura de la persona sobre el suelo, medida en pies. ¿Qué distancia promedio puede una persona ver un objeto desde una altura de$10$ pies? Redondear a la décima de milla más cercana.

Contestar

1. $\frac{11}{4}$

3. $80$

5. $30$

7. $2 \sqrt { 6 }$

9. $60 \pi$

11. $\$ 855$

13. $1.6$segundos

Ejercicio$\PageIndex{14}$

Multiplicar.

$\frac { x ^ { 10 } \cdot x ^ { 2 } } { x ^ { 5 } }$
$\frac { x ^ { 6 } \left( x ^ { 2 } \right) ^ { 4 } } { x ^ { 3 } }$
$- 7 x ^ { 2 } y z ^ { 3 } \cdot 3 x ^ { 4 } y ^ { 2 } z$
$3 a ^ { 2 } b ^ { 3 } c \left( - 4 a ^ { 2 } b c ^ { 4 } \right) ^ { 2 }$
$\frac { - 10 a ^ { 5 } b ^ { 0 } c ^ { - 4 } } { 25 a ^ { - 2 } b ^ { 2 } c ^ { - 3 } }$
$\frac { - 12 x ^ { - 6 } y ^ { - 2 } z } { 36 x ^ { - 3 } y ^ { 4 } z ^ { 6 } }$
$\left( - 2 x ^ { - 5 } y ^ { - 3 } z \right) ^ { - 4 }$
$\left( 3 x ^ { 6 } y ^ { - 3 } z ^ { 0 } \right) ^ { - 3 }$
$\left( \frac { - 5 a ^ { 2 } b ^ { 3 } } { c ^ { 5 } } \right) ^ { 2 }$
$\left( \frac { - 3 m ^ { 5 } } { 5 n ^ { 2 } } \right) ^ { 3 }$
$\left( \frac { - 2 a ^ { - 2 } b ^ { 3 } c } { 3 a b ^ { - 2 } c ^ { 0 } } \right) ^ { - 3 }$
$\left( \frac { 6 a ^ { 3 } b ^ { - 3 } c } { 2 a ^ { 7 } b ^ { 0 } c ^ { - 4 } } \right) ^ { - 2 }$

Contestar

1. $x ^ { 7 }$

3. $- 21 x ^ { 6 } y ^ { 3 } z ^ { 4 }$

5. $- \frac { 2 a ^ { 7 } } { 5 b ^ { 2 } c }$

7. $\frac { x ^ { 20 } y ^ { 12 } } { 16 z ^ { 4 } }$

9. $\frac { 25 a ^ { 4 } b ^ { 6 } } { c ^ { 10 } }$

11. $- \frac { 27 a ^ { 9 } } { 8 b ^ { 15 } c ^ { 3 } }$

Ejercicio$\PageIndex{15}$

Realizar las operaciones.

$\left( 4.3 \times 10 ^ { 22 } \right) \left( 3.1 \times 10 ^ { - 8 } \right)$
$\left( 6.8 \times 10 ^ { - 33 } \right) \left( 1.6 \times 10 ^ { 7 } \right)$
$\frac { 1.4 \times 10 ^ { - 32 } } { 2 \times 10 ^ { - 10 } }$
$\frac { 1.15 \times 10 ^ { 26 } } { 2.3 \times 10 ^ { - 7 } }$
El valor de una tableta nueva en dólares se puede estimar utilizando la fórmula$v = 450(t + 1)^{ −1}$ donde$t$ representa el número de años después de su compra. Utilice la fórmula para estimar el valor de la computadora tablet$2 \frac{1}{2}$ años después de su compra.
La velocidad de la luz es de aproximadamente$6.7 × 10^{8}$ millas por hora. Exprese esta velocidad en millas por minuto y determine la distancia que recorre la luz en$4$ minutos.

Contestar

1. $1.333 \times 10 ^ { 15 }$

3. $7 \times 10 ^ { - 23 }$

5. $\$ 128.57$

Ejercicio$\PageIndex{16}$

Simplificar.

$\left( x ^ { 2 } + 3 x - 5 \right) - \left( 2 x ^ { 2 } + 5 x - 7 \right)$
$\left( 6 x ^ { 2 } - 3 x + 5 \right) + \left( 9 x ^ { 2 } + 3 x - 4 \right)$
$\left( a ^ { 2 } b ^ { 2 } - a b + 6 \right) - ( a b + 9 ) + \left( a ^ { 2 } b ^ { 2 } - 10 \right)$
$\left( x ^ { 2 } - 2 y ^ { 2 } \right) - \left( x ^ { 2 } + 3 x y - y ^ { 2 } \right) - \left( 3 x y + y ^ { 2 } \right)$
$- \frac { 3 } { 4 } \left( 16 x ^ { 2 } + 8 x - 4 \right)$
$6 \left( \frac { 4 } { 3 } x ^ { 2 } - \frac { 3 } { 2 } x + \frac { 5 } { 6 } \right)$
$( 2 x + 5 ) ( x - 4 )$
$( 3 x - 2 ) \left( x ^ { 2 } - 5 x + 2 \right)$
$\left( x ^ { 2 } - 2 x + 5 \right) \left( 2 x ^ { 2 } - x + 4 \right)$
$\left( a ^ { 2 } + b ^ { 2 } \right) \left( a ^ { 2 } - b ^ { 2 } \right)$
$( 2 a + b ) \left( 4 a ^ { 2 } - 2 a b + b ^ { 2 } \right)$
$( 2 x - 3 ) ^ { 2 }$
$( 3 x - 1 ) ^ { 3 }$
$( 2 x + 3 ) ^ { 4 }$
$\left( x ^ { 2 } - y ^ { 2 } \right) ^ { 2 }$
$\left( x ^ { 2 } y ^ { 2 } + 1 \right) ^ { 2 }$
$\frac { 27 a ^ { 2 } b - 9 a b + 81 a b ^ { 2 } } { 3 a b }$
$\frac { 125 x ^ { 3 } y ^ { 3 } - 25 x ^ { 2 } y ^ { 2 } + 5 x y ^ { 2 } } { 5 x y ^ { 2 } }$
$\frac { 2 x ^ { 3 } - 7 x ^ { 2 } + 7 x - 2 } { 2 x - 1 }$
$\frac { 12 x ^ { 3 } + 5 x ^ { 2 } - 7 x - 3 } { 4 x + 3 }$
$\frac { 5 x ^ { 3 } - 21 x ^ { 2 } + 6 x - 3 } { x - 4 }$
$\frac { x ^ { 4 } + x ^ { 3 } - 3 x ^ { 2 } + 10 x - 1 } { x + 3 }$
$\frac { a ^ { 4 } - a ^ { 3 } + 4 a ^ { 2 } - 2 a + 4 } { a ^ { 2 } + 2 }$
$\frac { 8 a ^ { 4 } - 10 } { a ^ { 2 } - 2 }$

Contestar

1. $- x ^ { 2 } - 2 x + 2$

3. $2 a ^ { 2 } b ^ { 2 } - 2 a b - 13$

5. $- 12 x ^ { 2 } - 6 x + 3$

7. $2 x ^ { 2 } - 3 x - 20$

9. $2 x ^ { 4 } - 5 x ^ { 3 } + 16 x ^ { 2 } - 13 x + 20$

11. $8 a ^ { 3 } + b ^ { 3 }$

13. $27 x ^ { 3 } - 27 x ^ { 2 } + 9 x - 1$

15. $x ^ { 4 } - 2 x ^ { 2 } y ^ { 2 } + y ^ { 4 }$

17. $9 a + 27 b - 3$

19. $x ^ { 2 } - 3 x + 2$

21. $5 x ^ { 2 } - x + 2 + \frac { 5 } { x - 4 }$

23. $a ^ { 2 } - a + 2$

Ejercicio$\PageIndex{17}$

Resolver.

$6 x - 8 = 2$
$12 x - 5 = 3$
$\frac { 5 } { 4 } x - 3 = \frac { 1 } { 2 }$
$\frac { 5 } { 6 } x - \frac { 1 } { 4 } = \frac { 3 } { 2 }$
$\frac { 9 x + 2 } { 3 } = \frac { 5 } { 6 }$
$\frac { 3 x - 8 } { 10 } = \frac { 5 } { 2 }$
$3 a - 5 - 2 a = 4 a - 6$
$8 - 5 y + 2 = 4 - 7 y$
$5 x - 6 - 8 x = 1 - 3 x$
$17 - 6 x - 10 = 5 x + 7 - 11 x$
$5 ( 3 x + 3 ) - ( 10 x - 4 ) = 4$
$6 - 2 ( 3 x - 1 ) = - 4 ( 1 - 3 x )$
$9 - 3 ( 2 x + 3 ) + 6 x = 0$
$- 5 ( x + 2 ) - ( 4 - 5 x ) = 1$
$\frac { 5 } { 9 } ( 6 y + 27 ) = 2 - \frac { 1 } { 3 } ( 2 y + 3 )$
$4 - \frac { 4 } { 5 } ( 3 a + 10 ) = \frac { 1 } { 10 } ( 4 - 2 a )$
Resolver para$s : A = \pi r ^ { 2 } + \pi r s$
Resolver para$x : y = m x + b$
Un entero más grande es$3$ más de dos veces otro. Si su suma dividida por$2$ es$9$, encuentra los enteros.
La suma de tres enteros impares consecutivos es$171$. Encuentra los enteros.
La longitud de un rectángulo es$3$ metros menos del doble de su ancho. Si el perímetro mide$66$ metros, encuentra el largo y ancho.
¿Cuánto tiempo se tardará$$124$ en$$500$ ganar en intereses simples ganando$6.2$% interés anual?
Sally tardó$3 \frac{1}{2}$ horas en conducir los$147$ kilómetros a casa desde la casa de su abuela. ¿Cuál era su velocidad promedio?
Jeannine invirtió su bono de$$8,300$ en dos cuentas. Una cuenta ganó$3 \frac{1}{2}$% interés simple y la otra ganó$4 \frac{3}{4}$% interés simple. Si su interés total por un año fue$$341.75$, ¿cuánto invirtió en cada cuenta?

Contestar

1. $\frac{5}{3}$

3. $\frac{14}{5}$

5. $\frac{1}{18}$

7. $\frac{1}{3}$

9. $\varnothing$

11. $-3$

13. $\mathbb { R }$

15. $-\frac{7}{2}$

17. $s = \frac { A - \pi r ^ { 2 } } { \pi r }$

19. $5,13$

21. Largo:$21$ metros; Ancho:$12$ metros

23. $42$millas por hora

Ejercicio$\PageIndex{18}$

Resolver. Grafique todas las soluciones en una recta numérica y proporcione la notación de intervalo correspondiente.

$5 x - 7 < 18$
$2 x - 1 > 2$
$9 - x \leq 3$
$3 - 7 x \geq 10$
$61 - 3 ( x + 3 ) > 13$
$7 - 3 ( 2 x - 1 ) \geq 6$
$\frac { 1 } { 3 } ( 9 x + 15 ) - \frac { 1 } { 2 } ( 6 x - 1 ) < 0$
$\frac { 2 } { 3 } ( 12 x - 1 ) + \frac { 1 } { 4 } ( 1 - 32 x ) < 0$
$20 + 4 ( 2 a - 3 ) \geq \frac { 1 } { 2 } a + 2$
$\frac { 1 } { 3 } \left( 2 x + \frac { 3 } { 2 } \right) - \frac { 1 } { 4 } x < \frac { 1 } { 2 } \left( 1 - \frac { 1 } { 2 } x \right)$
$- 4 \leq 3 x + 5 < 11$
$5 < 2 x + 15 \leq 13$
$- 1 < 4 ( x + 1 ) - 1 < 9$
$0 \leq 3 ( 2 x - 3 ) + 1 \leq 10$
$- 1 < \frac { 2 x - 5 } { 4 } < 1$
$- 2 \leq \frac { 3 - x } { 3 } < 1$
$2 x + 3 < 13 \text { and } 4 x - 1 > 10$
$3 x - 1 \leq 8 \text { and } 2 x + 5 \geq 23$
$5 x - 3 < - 2 \text { or } 5 x - 3 > 2$
$1 - 3 x \leq - 1 \text { or } 1 - 3 x \geq 1$
$5 x + 6 < 6 \text { or } 9 x - 2 > - 11$
$2 ( 3 x - 1 ) < - 16 \text { or } 3 ( 1 - 2 x ) < - 15$
Jerry anotó$90, 85, 92$, y$76$ en los primeros cuatro exámenes de álgebra. ¿Qué debe puntuar en el quinto examen para que su promedio sea al menos$80$?
Si$6$ grados menores que$3$ veces un ángulo es entre$90$ grados y$180$ grados, entonces ¿cuáles son los límites del ángulo original?

Contestar

1. $( - \infty , 5 )$;

Figura 1.E.5

3. $[ 6 , \infty )$;

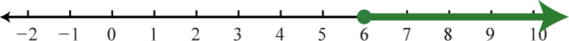
Figura 1.E.6

5. $( - \infty , 13 )$;

Figura 1.E.7

7. $\varnothing$;

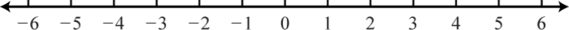
Figura 1.E.8

9. $\left[ - \frac { 4 } { 5 } , \infty \right)$;

Figura 1.E.9

11. $[ - 3,2 )$;

Figura 1.E.10

13. $\left( - 1 , \frac { 3 } { 2 } \right)$;

Figura 1.E.11

15. $\left( \frac { 1 } { 2 } , \frac { 9 } { 2 } \right)$;

Figura 1.E.12

17. $\left( \frac { 11 } { 4 } , 5 \right)$;

Figura 1.E.13

19. $\left( - \infty , \frac { 1 } { 5 } \right) \cup ( 1 , \infty )$;

Figura 1.E.14

21. $\mathbb { R }$;

Figura 1.E.15

23. Jerry debe anotar al menos$57$ en el quinto examen.

Examen de muestra

Ejercicio$\PageIndex{19}$

Simplificar.

$5 - 3 \left( 12 - \left| 2 - 5 ^ { 2 } \right| \right)$
$\left( - \frac { 1 } { 2 } \right) ^ { 2 } - \left( 3 - 2 \left| - \frac { 3 } { 4 } \right| \right) ^ { 3 }$
$- 7 \sqrt { 60 }$
$5 \sqrt [ 3 ] { - 32 }$
Encuentra la diagonal de un cuadrado con lados que miden$6$ centímetros.

Contestar

1. $38$

3. $- 14 \sqrt { 15 }$

5. $6 \sqrt { 2 }$centímetros

Ejercicio$\PageIndex{20}$

Simplificar

$- 5 x ^ { 2 } y z ^ { - 1 } \left( 3 x ^ { 3 } y ^ { - 2 } z \right)$
$\left( \frac { - 2 a ^ { - 4 } b ^ { 2 } c } { a ^ { - 3 } b ^ { 0 } c ^ { 2 } } \right) ^ { - 3 }$
$2 \left( 3 a ^ { 2 } b ^ { 2 } + 2 a b - 1 \right) - a ^ { 2 } b ^ { 2 } + 2 a b - 1$
$\left( x ^ { 2 } - 6 x + 9 \right) - \left( 3 x ^ { 2 } - 7 x + 2 \right)$
$( 2 x - 3 ) ^ { 3 }$
$( 3 a - b ) \left( 9 a ^ { 2 } + 3 a b + b ^ { 2 } \right)$
$\frac { 6 x ^ { 4 } - 17 x ^ { 3 } + 16 x ^ { 2 } - 18 x + 13 } { 2 x - 3 }$

Contestar

2. $- \frac { a ^ { 3 } c ^ { 3 } } { 8 b ^ { 6 } }$

4. $- 2 x ^ { 2 } + x + 7$

6. $27 a ^ { 3 } - b ^ { 3 }$

Ejercicio$\PageIndex{21}$

Resolver.

$\frac { 4 } { 5 } x - \frac { 2 } { 15 } = 2$
$\frac { 3 } { 4 } ( 8 x - 12 ) - \frac { 1 } { 2 } ( 2 x - 10 ) = 16$
$12 - 5 ( 3 x - 1 ) = 2 ( 4 x + 3 )$
$\frac { 1 } { 2 } ( 12 x - 2 ) + 5 = 4 \left( \frac { 3 } { 2 } x - 8 \right)$
Resolver para$y : a x + b y = c$

Contestar

1. $\frac{8}{3}$

3. $\frac{11}{23}$

5. $y = \frac { c - a x } { b }$

Ejercicio$\PageIndex{22}$

Resolver. Grafique las soluciones en una recta numérica y dé la notación de intervalo correspondiente.

$2 ( 3 x - 5 ) - ( 7 x - 3 ) \geq 0$
$2 ( 4 x - 1 ) - 4 ( 5 + 2 x ) < - 10$
$- 6 \leq \frac { 1 } { 4 } ( 2 x - 8 ) < 4$
$3 x - 7 > 14 \text { or } 3 x - 7 < - 14$

Contestar

2. $\mathbb { R }$;

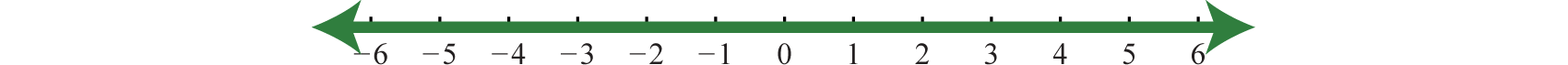
Figura 1.E.16

4. $\left( - \infty , - \frac { 7 } { 3 } \right) \cup ( 7 , \infty )$;

Figura 1.E.17

Ejercicio$\PageIndex{23}$

Usa álgebra para resolver lo siguiente.

Grados Fahrenheit$F$ viene dado por la fórmula$F = \frac{9}{5} C + 32$ donde C representa grados Celsius. ¿Cuál es el equivalente Fahrenheit a$35$° Celsius?
La longitud de un rectángulo es$5$ pulgadas menos que su ancho. Si el perímetro es$134$ pulgadas, encuentra el largo y ancho del rectángulo.
Melanie invirtió$4,500$ en dos cuentas separadas. Ella invirtió parte en un CD que ganaba$3.2$% interés simple y el resto en una cuenta de ahorro que ganaba$2.8$% interés simple. Si el interés simple total de un año fue$$138.80$, ¿cuánto invirtió en cada cuenta?
Un auto de alquiler cuesta$$45.00$ por día más$$0.48$ por milla conducida. Si el costo total de un alquiler de un día es como máximo$$105$, ¿cuántas millas se pueden conducir?

Contestar

2. Largo:$31$ pulgadas; ancho:$36$ pulgadas

4. El automóvil se puede conducir como máximo en$125$ millas.