1.7: Resolver ecuaciones lineales

Última actualización
Guardar como PDF

Page ID: 109800

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Utilice las propiedades de igualdad para resolver ecuaciones lineales básicas.
Identificar y resolver ecuaciones lineales condicionales, identidades y contradicciones.
Borrar fracciones de ecuaciones.
Configura y resuelve ecuaciones lineales.

Resolver ecuaciones lineales básicas

Una ecuación ¹²⁹ es una declaración que indica que dos expresiones algebraicas son iguales. Una ecuación lineal con una variable ¹³⁰,$x$, es una ecuación que se puede escribir en la forma estándar$ax + b = 0$ donde$a$ y$b$ son números reales y$a ≠ 0$. Por ejemplo

$3 x - 12 = 0$

Una solución ¹³¹ a una ecuación lineal es cualquier valor que pueda reemplazar la variable para producir una declaración verdadera. La variable en la ecuación lineal$3x − 12 = 0$ es$x$ y la solución es$x = 4$. Para verificar esto, sustituya$4$ el valor por$x$ y verifique que obtenga una declaración verdadera.

$\begin{aligned} 3 x - 12 & = 0 \\ 3 ( \color{Cerulean}{4}\color{Black}{ )} - 12 & = 0 \\ 12 - 12 & = 0 \\ 0 & = 0 \:\: \color{Cerulean}{✓} \end{aligned}$

Alternativamente, cuando una ecuación es igual a una constante, podemos verificar una solución sustituyendo el valor in por la variable y mostrando que el resultado es igual a esa constante. En este sentido, decimos que las soluciones “satisfacen la ecuación”.

Ejemplo$\PageIndex{1}$:

¿Es$a=−\frac{1}{2}$ una solución para$−10a+5=25$?

Solución

Recordemos que al evaluar expresiones, es una buena práctica reemplazar primero todas las variables por paréntesis, y luego sustituir los valores apropiados. Al hacer uso de paréntesis, evitamos algunos errores comunes a la hora de trabajar el orden de las operaciones.

$- 10 a + 5 = - 10 ( \color{Cerulean}{- \frac { 1 } { 2 }} \color{Black}{ ) +} 5 = 5 + 5 = 10 \neq 25\:\: \color{red}{✗}$

Respuesta:

No,$a=−\frac{1}{2}$ no satisface la ecuación.

Desarrollar técnicas para resolver diversas ecuaciones algebraicas es uno de nuestros principales objetivos en álgebra. En esta sección se revisan las técnicas básicas utilizadas para resolver ecuaciones lineales con una variable. Comenzamos definiendo las ecuaciones equivalentes ¹³² como ecuaciones con el mismo conjunto de soluciones.

$\left. \begin{aligned} 3 x - 5 & = 16 \\ 3 x & = 21 \\ x & = 7 \end{aligned} \right\} \quad \color{Cerulean}{Equivalent \:equations}$

Aquí podemos ver que las tres ecuaciones lineales son equivalentes porque comparten el mismo conjunto de soluciones, es decir,$\{7\}$. Para obtener ecuaciones equivalentes, utilice las siguientes propiedades de igualdad ¹³³. Dadas expresiones algebraicas$A$ y$B$, donde$c$ es un número distinto de cero:

Mesa$\PageIndex{1}$
Adición propiedad de igualdad:	Si$A=B$, entonces$A\color{Cerulean}{+c}\color{Black}{=} B\color{Cerulean}{+c}$
Resta propiedad de igualdad:	Si$A=B$, entonces$A\color{Cerulean}{-c}\color{Black}{-}B\color{Cerulean}{-c}$
Multiplicación propiedad de igualdad:	Si$A=B$, entonces$\color{Cerulean}{c}\color{Black}{A}=\color{Cerulean}{c}\color{Black}{B}$
División propiedad de igualdad:	Si$A=B$, entonces$\frac{A}{\color{Cerulean}{c}}\color{Black}{=}\frac{B}{\color{Cerulean}{c}}$

Nota

Se evita cuidadosamente multiplicar o dividir ambos lados de una ecuación por$0$. Dividir por$0$ es indefinido y multiplicar ambos lados por$0$ resultados en la ecuación$0 = 0$.

Resolvemos ecuaciones algebraicas aislando la variable con un coeficiente de 1. Si se le da una ecuación lineal de la forma$ax + b = c$, entonces podemos resolverla en dos pasos. En primer lugar, utilizar la propiedad de igualdad apropiada de suma o resta para aislar el término variable. A continuación, aísle la variable usando la propiedad de igualdad de multiplicación o división. Comprobando la solución en los siguientes ejemplos se deja al lector.

Ejemplo$\PageIndex{2}$:

Resolver:$7x − 2 = 19$.

Solución

$\begin{aligned} 7 x - 2 & = 19 \\ 7 x - 2 \color{Cerulean}{+ 2} & = 19 \color{Cerulean}{+ 2} \quad Add\: 2\: to\: both\: sides. \\ 7 x & = 21 \\ \frac { 7 x } { \color{Cerulean}{7} } & = \frac { 21 } { \color{Cerulean}{7} } \quad \color{Cerulean}{Divide\: both\: sides\: by\: 7.} \\ x & = 3 \end{aligned}$

Respuesta:

La solución es$3$.

Ejemplo$\PageIndex{3}$:

Resolver:$56 = 8 + 12y$.

Solución

Cuando ningún signo precede al término, se entiende que es positivo. En otras palabras, piensa en esto como$56 = +8 + 12y$. Por lo tanto, comenzamos restando a ambos$8$ lados del signo igual.

$\begin{aligned} 56 \color{Cerulean}{- 8} & = 8 + 12 y \color{Cerulean}{- 8} \\ 48 & = 12 y \\ \frac { 48 } { \color{Cerulean}{12} } & = \frac { 12 y } { \color{Cerulean}{12} } \\ 4 & = y \end{aligned}$

No importa de qué lado elijamos aislar la variable porque la propiedad simétrica ¹³⁴ establece que$4 = y$ es equivalente a$y = 4$.

Respuesta:

La solución es$4$.

Ejemplo$\PageIndex{4}$:

Resolver:$\frac { 5 } { 3 } x + 2 = - 8$.

Solución

Aísle el término variable usando la propiedad de suma de igualdad, y luego multiplique ambos lados de la ecuación por el recíproco del coeficiente$\frac{5}{3}$.

\ begin {alineado}\ frac {5} {3} x + 2 & = - 8\\\ frac {5} {3} x + 2\ color {cerúleo} {- 2} & = - 8\ color {cerúleo} {- 2}\ quad\ color {cerúleo} {Restar\: 2\: on\: ambos\: lados.}\\\ frac {5} {3} x & = - 10\\\ color {cerúleo} {\ frac {3} {5}}\ color {Negro} {\ cdot}\ frac {5} {3} x & =\ color {cerúleo} {\ frac {3} {\ cancel {5}}}\ color {Negro} {\ cdot} (\ overset {-2} {\ cancel {-10}})\ quad\ color {cerúleo} {Multiplicar\ :ambos\ :lados\: por\:\ frac {3} {5}.}\\ 1x & = 3\ cdot (- 2)\\ x & = - 6\ fin {alineado}

Respuesta:

La solución es$−6$.

En resumen, para retener ecuaciones equivalentes, debemos realizar la misma operación en ambos lados de la ecuación.

Ejercicio$\PageIndex{1}$

Resolver:$\frac { 2 } { 3 } x + \frac { 1 } { 2 } = - \frac { 5 } { 6 }$.

Responder

$x=-2$

www.youtube.com/v/cqwqxs9ad6M

Lineamientos generales para resolver ecuaciones lineales

Normalmente, las ecuaciones lineales no se dan en forma estándar, por lo que resolverlas requiere pasos adicionales. Al resolver ecuaciones lineales, el objetivo es determinar qué valor, en su caso, producirá una declaración verdadera cuando se sustituya en la ecuación original. Haga esto aislando la variable siguiendo los siguientes pasos:

Paso 1: Simplifica ambos lados de la ecuación usando el orden de las operaciones y combina todos los términos similares en el mismo lado del signo igual.
Paso 2: Usa las propiedades apropiadas de igualdad para combinar términos similares en lados opuestos del signo igual. El objetivo es obtener el término variable en un lado de la ecuación y el término constante en el otro.
Paso 3: Divide o multiplica según sea necesario para aislar la variable.
Paso 4: Comprueba si la respuesta resuelve la ecuación original.

A menudo nos encontraremos con ecuaciones lineales donde las expresiones a cada lado del signo igual pueden simplificarse. Si este es el caso, entonces lo mejor es simplificar cada lado primero antes de resolver. Normalmente esto implica combinar términos similares al mismo lado.

Nota

En este punto de nuestro estudio del álgebra el uso de las propiedades de la igualdad debería parecer rutinario. Por lo tanto, mostrar estos pasos en este texto, generalmente en azul, se vuelve opcional.

Ejemplo$\PageIndex{5}$:

Resolver:$- 4 a + 2 - a = 1$.

Solución

Primero combina los términos similares en el lado izquierdo del signo igual.

$\begin{aligned} - 4 a + 2 - a = 1 & \quad \color{Cerulean}{ Combine\: same-side\: like\: terms.} \\ - 5 a + 2 = 1 & \quad\color{Cerulean} { Subtract\: 2\: on\: both\: sides.} \\ - 5 a = - 1 & \quad\color{Cerulean} { Divide\: both\: sides\: by\: - 5.} \\ a = \frac { - 1 } { - 5 } = \frac { 1 } { 5 } \end{aligned}$

Siempre use la ecuación original para verificar si la solución es correcta.

$\begin{aligned} - 4 a + 2 - a & = - 4 \left( \color{OliveGreen}{\frac { 1 } { 5 }} \right) + 2 - \color{OliveGreen}{\frac { 1 } { 5 }} \\ & = - \frac { 4 } { 5 } + \frac { 2 } { 1 } \cdot \color{Cerulean}{\frac { 5 } { 5 }}\color{Black}{ -} \frac { 1 } { 5 } \\ & = \frac { - 4 + 10 + 1 } { 5 } \\ & = \frac { 5 } { 5 } = 1 \:\:\color{Cerulean}{✓} \end{aligned}$

Respuesta:

La solución es$\frac{1}{5}$.

Dada una ecuación lineal en la forma$ax + b = cx + d$, comenzamos el proceso de resolución combinando términos similares en lados opuestos del signo igual. Para ello, usa la propiedad de suma o resta de igualdad para colocar términos similares del mismo lado para que puedan combinarse. En los ejemplos que quedan, el cheque se deja al lector.

Ejemplo$\PageIndex{6}$:

Resolver:$−2y − 3 = 5y + 11$.

Solución

Restar$5y$ en ambos lados para que podamos combinar los términos que involucran y en el lado izquierdo.

$\begin{array} { c } { - 2 y - 3 \color{Cerulean}{- 5 y}\color{Black}{ =} 5 y + 11 \color{Cerulean}{- 5 y} } \\ { - 7 y - 3 = 11 } \end{array}$

A partir de aquí, resolver utilizando las técnicas desarrolladas previamente.

$\begin{aligned} - 7 y - 3 & = 11 \quad\color{Cerulean}{Add\: 3\: to\: both\: sides.} \\ - 7 y & = 14 \\ y & = \frac { 14 } { - 7 } \quad\color{Cerulean}{Divide\: both\: sides\: by\: -7.} \\ y & = - 2 \end{aligned}$

Respuesta:

La solución es$−2$.

La resolución a menudo requerirá la aplicación de la propiedad distributiva.

Ejemplo$\PageIndex{7}$:

Resolver:$- \frac { 1 } { 2 } ( 10 x - 2 ) + 3 = 7 ( 1 - 2 x )$.

Solución

Simplifique primero las expresiones lineales a ambos lados del signo igual.

$\begin{aligned} - \frac { 1 } { 2 } ( 10 x - 2 ) + 3 = 7 ( 1 - 2 x ) & \quad\color{Cerulean} { Distribute } \\ - 5 x + 1 + 3 = 7 - 14 x & \quad\color{Cerulean} { Combine\: same-side\: like\: terms. } \\ - 5 x + 4 = 7 - 14 x & \quad\color{Cerulean} { Combine\: opposite-side\: like\: terms. } \\ 9 x = 3 & \quad\color{Cerulean} { Solve. } \\ x = \frac { 3 } { 9 } = \frac { 1 } { 3 } \end{aligned}$

Respuesta:

La solución es$\frac{1}{3}$.

Ejemplo$\PageIndex{8}$:

Resolver:$5(3−a)−2(5−2a)=3$.

Solución

Comience por aplicar la propiedad distributiva.

$\begin{aligned} 5 ( 3 - a ) - 2 ( 5 - 2 a ) & = 3 \\ 15 - 5 a - 10 + 4 a & = 3 \\ 5 - a & = 3 \\ - a & = - 2 \end{aligned}$

Aquí señalamos que$−a$ es equivalente a$−1a$; por lo tanto, elegimos dividir ambos lados de la ecuación por$−1$.

$\begin{array} { c } { - a = - 2 } \\ { \frac { - 1 a } { \color{Cerulean}{- 1} }\color{Black}{ =} \frac { - 2 } { \color{Cerulean}{- 1} } } \\ { a = 2 } \end{array}$

Alternativamente, podemos multiplicar ambos lados de$−a=−2$ por uno negativo y lograr el mismo resultado.

$\begin{aligned} - a & = - 2 \\ \color{Cerulean}{( - 1 )}\color{Black}{ (} - a ) & = \color{Cerulean}{( - 1 )}\color{Black}{ (} - 2 ) \\ a & = 2 \end{aligned}$

Respuesta:

La solución es$2$.

Ejercicio$\PageIndex{2}$

Resolver:$6 - 3 ( 4 x - 1 ) = 4 x - 7$.

Responder

$x=1$

www.youtube.com/v/naiazrfju-o

Hay tres tipos diferentes de ecuaciones. Hasta este punto, hemos estado resolviendo ecuaciones condicionales ¹³⁵. Estas son ecuaciones que son ciertas para valores particulares. Una identidad ¹³⁶ es una ecuación que es verdadera para todos los valores posibles de la variable. Por ejemplo,

$x = x \quad\color{Cerulean}{Identity}$

tiene un conjunto de soluciones que consta de todos los números reales,$ℝ$. Una contradicción ¹³⁷ es una ecuación que nunca es cierta y por lo tanto no tiene soluciones. Por ejemplo,

$x+1=x\quad\color{Cerulean}{Contradiction}$

no tiene solución. Utilizamos el conjunto vacío,$Ø$, para indicar que no hay soluciones.

Si el resultado final de resolver una ecuación es una afirmación verdadera, como$0 = 0$, entonces la ecuación es una identidad y cualquier número real es una solución. Si resolver resulta en una declaración falsa, como$0 = 1$, entonces la ecuación es una contradicción y no hay solución.

Ejemplo$\PageIndex{9}$:

Resolver:$4 (x + 5) + 6 = 2 (2x + 3)$.

Solución

$\begin{aligned} 4 ( x + 5 ) + 6 & = 2 ( 2 x + 3 ) \\ 4 x + 20 + 6 & = 4 x + 6 \\ 4 x + 26 & = 4 x + 6 \\ 26 & = 6\:\: \color{red}{✗} \end{aligned}$

Resolver lleva a una declaración falsa; por lo tanto, la ecuación es una contradicción y no hay solución.

Respuesta:

$Ø$

Ejemplo$\PageIndex{10}$:

Resolver:$3 (3y + 5) + 5 = 10 (y + 2) − y$.

Solución

$\begin{aligned} 3 ( 3 y + 5 ) + 5 & = 10 ( y + 2 ) - y \\ 9 y + 15 + 5 & = 10 y + 20 - y \\ 9 y + 20 & = 9 y + 20 \\ 9 y & = 9 y \\ 0 & = 0 \:\:\color{Cerulean}{✓} \end{aligned}$

Resolver conduce a una afirmación verdadera; por lo tanto, la ecuación es una identidad y cualquier número real es una solución.

Respuesta:

$ℝ$

Los coeficientes de las ecuaciones lineales pueden ser cualquier número real, incluso decimales y fracciones. Cuando este es el caso es posible utilizar la propiedad de multiplicación de igualdad para borrar los coeficientes fraccionarios y obtener coeficientes enteros en un solo paso. Si se le dan coeficientes fraccionarios, entonces multiplique ambos lados de la ecuación por el mínimo común múltiplo de los denominadores (LCD).

Ejemplo$\PageIndex{11}$:

Resolver:$\frac { 1 } { 3 } x + \frac { 1 } { 5 } = \frac { 1 } { 5 } x - 1$.

Solución

Despeja las fracciones multiplicando ambos lados por el múltiplo menos común de los denominadores dados. En este caso, es el$LCD (3, 5) = 15$.

$\begin{aligned} \color{Cerulean}{15}\color{Black}{ \cdot} \left( \frac { 1 } { 3 } x + \frac { 1 } { 5 } \right) & = \color{Cerulean}{15}\color{Black}{ \cdot} \left( \frac { 1 } { 5 } x - 1 \right) \quad \color{Cerulean}{Multiply\: both\: sides\: by\: 15.} \\ \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 3 } x + \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 5 } & = \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 5 } x - \color{Cerulean}{15}\color{Black}{ \cdot} 1\quad\color{Cerulean}{Simplify.} \\ 5 x + 3 & = 3 x - 15\quad\quad\quad\color{Cerulean}{Solve.} \\ 2 x & = - 18 \\ x & = \frac { - 18 } { 2 } = - 9 \end{aligned}$

Respuesta:

La solución es$−9$.

Es importante saber que esta técnica sólo funciona para ecuaciones. No intentes borrar fracciones al simplificar expresiones. Como recordatorio:

Mesa$\PageIndex{2}$
Expresión	Ecuación
$\frac { 1 } { 2 } x + \frac { 5 } { 3 }$	$\frac { 1 } { 2 } x + \frac { 5 } { 3 }=0$

Simplificamos expresiones y resolvemos ecuaciones. Si multiplicas una expresión por$6$, cambiarás el problema. Sin embargo, si multiplicas ambos lados de una ecuación por$6$, obtienes una ecuación equivalente.

Mesa$\PageIndex{3}$
Incorrecto	Corregir
$ \frac { 1 } { 2 } x + \frac { 5 } { 3 }$ $\begin{aligned} \neq & \color{red}{6 \cdot}\color{Black}{ \left( \frac { 1 } { 2 } x + \frac { 5 } { 3 } \right)} \\ = & 3 x + 10 \quad \color{red}{✗} \end{aligned}$	$\begin{aligned} \frac { 1 } { 2 } x + \frac { 5 } { 3 } & = 0 \\ \color{Cerulean}{6 \cdot}\color{Black}{ \left( \frac { 1 } { 2 } x + \frac { 5 } { 3 } \right)} & = \color{Cerulean}{6 \cdot}\color{Black}{ 0} \\ 3 x + 10 & = 0\quad\color{Cerulean}{✓} \end{aligned}$

Aplicaciones que implican ecuaciones lineales

El álgebra simplifica el proceso de resolución de problemas del mundo real. Esto se hace usando letras para representar incógnitas, replanteando problemas en forma de ecuaciones y ofreciendo técnicas sistemáticas para resolver esas ecuaciones. Para resolver problemas utilizando álgebra, primero traduzca la redacción del problema en enunciados matemáticos que describan las relaciones entre la información dada y las incógnitas. Por lo general, esta traducción a declaraciones matemáticas es el paso difícil en el proceso. La clave de la traducción es leer atentamente el problema e identificar ciertas palabras y frases clave.

Mesa$\PageIndex{4}$
Palabras clave	Traducción
Suma, incrementada en, más de, más, sumada a, total	$+$
Diferencia, disminuida por, restada de, menos, menos	$-$
Producto, multiplicado por, de veces, dos veces	$\cdot$
Cociente, dividido por, ratio, per	$÷$
Es, total, resultado	$=$

Al traducir oraciones en declaraciones matemáticas, asegúrese de leer la oración varias veces y analizar las palabras y frases clave. Es importante identificar primero la variable, “dejar que x represente...” y declarar en palabras cuál es la cantidad desconocida. Este paso no sólo hace que nuestro trabajo sea más legible, sino que también nos obliga a pensar en lo que estamos buscando.

Ejemplo$\PageIndex{12}$:

Cuando$6$ se resta del doble de la suma de un número y$8$ el resultado es$5$. Encuentra el número.

Solución

Que n represente el número desconocido.

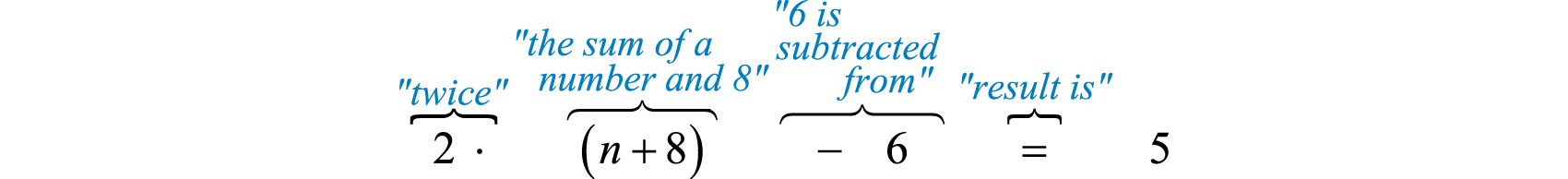
Para entender por qué incluimos los paréntesis en la configuración, se debe estudiar la estructura de las dos frases siguientes y sus traducciones:

Mesa$\PageIndex{5}$
“el doble de la suma de un número y 8”	2 (n+8)
“la suma de dos veces por número* y 8*”	2n+8

La clave era enfocarnos en la frase “el doble de la suma”, esto nos impulsó a agrupar la suma entre paréntesis y luego multiplicarnos por$2$. Después de traducir la oración en una declaración matemática resolvemos luego.

$\begin{aligned} 2 ( n + 8 ) - 6 & = 5 \\ 2 n + 16 - 6 & = 5 \\ 2 n + 10 & = 5 \\ 2 n & = - 5 \\ n & = \frac { - 5 } { 2 } \end{aligned}$

Cheque.

$\begin{aligned} 2 ( n + 8 ) - 6 & = 2 \left( \color{Cerulean}{- \frac { 5 } { 2 }}\color{Black}{ +} 8 \right) - 6 \\ & = 2 \left( \frac { 11 } { 2 } \right) - 6 \\ & = 11 - 6 \\ & = 5 \quad\color{Cerulean}{✓}\end{aligned}$

Respuesta:

El número es$−\frac{5}{2}$.

Se siguen pautas generales para la configuración y solución de problemas verbales.

Paso 1: Lee el problema varias veces, identifica las palabras y frases clave, y organiza la información dada.
Paso 2: Identificar las variables asignando una letra o expresión a las cantidades desconocidas.
Paso 3: Traducir y configurar una ecuación algebraica que modele el problema.
Paso 4: Resolver la ecuación algebraica resultante.
Paso 5: Finalmente, contesta la pregunta en forma de oración y asegúrate de que tenga sentido (compruébalo).

Por ahora, configura todas tus ecuaciones usando solo una variable. Evita dos variables buscando una relación entre las incógnitas.

Ejemplo$\PageIndex{13}$:

Un rectángulo tiene$92$ medidores perimetrales. El largo es$2$ metros menor que$3$ veces el ancho. Encuentra las dimensiones del rectángulo.

Solución

La frase “La longitud es de 2 metros menos de 3 veces la anchura”, nos da la relación entre las dos variables.

Dejar$w$ representar el ancho del rectángulo.

Dejar$3w−2$ representar la longitud.

La frase “Un rectángulo tiene un perímetro que mide 92 metros” sugiere una configuración algebraica. Sustituya$92$ el perímetro y la expresión$3w−2$ por la longitud en la fórmula apropiada de la siguiente manera:

$P = \quad2 l\:\:\:\:\: +\:\:\: 2 w$

$\color{Cerulean}{\downarrow} \quad\:\:\:\quad \color{Cerulean}{\downarrow}\quad\quad\quad\quad$

$\color{OliveGreen}{92}\color{Black}{ =} 2 (\color{OliveGreen}{ 3 w - 2}\color{Black}{ )} + 2 w$

Una vez que haya configurado una ecuación algebraica con una variable, resuelva para el ancho,$w$.

$\begin{array} { l } { 92 = 2 ( 3 w - 2 ) + 2 w \color{Cerulean}{ Distribute. } } \\ { 92 = 6 w - 4 + 2 w \quad\: \color{Cerulean} { Combine\: like\: terms. } } \\ { 92 = 8 w - 4 \quad\quad\quad\:\:\:\color{Cerulean} { Solve\: for\: w. } } \\ { 96 = 8 w } \\ { 12 = w } \end{array}$

$3w−2$Utilízalo para encontrar la longitud.

$l = 3 w - 2 = 3 ( \color{OliveGreen}{12}\color{Black}{ )} - 2 = 36 - 2 = 34$

Para verificar, asegúrese de que el perímetro sea$92$ metros.

$\begin{aligned} P & = 2 l + 2 w \\ & = 2 ( 34 ) + 2 ( 12 ) \\ & = 68 + 24 \\ & = 92 \end{aligned}$

Respuesta:

El rectángulo mide$12$ metros por$34$ metros.

Ejemplo$\PageIndex{14}$:

Dada una tasa de interés anual$4 \frac{3}{8}$%, ¿cuánto tiempo tardará$$437.50$ en$$2,500$ rendir en interés simple?

Solución

Que t represente el tiempo necesario para ganar$$437.50$ en$4 \frac{3}{8}$%. Organizar la información necesaria para utilizar la fórmula por simple interés,$I=prt$.

Mesa$\PageIndex{6}$
Dados intereses para el periodo de tiempo:	$I=$437.50$
Dado principal:	$p=$2,500$
Tasa dada:	$r= 4 \frac{3}{8}$%$=4.375$%$=0.04375$

A continuación, sustituya todas las cantidades conocidas en la fórmula y luego resuelva por el único desconocido, t.

$\begin{aligned} I & = p r t \\ \color{OliveGreen}{437.50} & \color{Black}{=} \color{OliveGreen}{2500}\color{Black}{ (}\color{OliveGreen}{ 0.04375}\color{Black}{ )} t \\ 437.50 & = 109.375 t \\ \frac{437.50}{\color{Cerulean}{109.375}} & \color{Black}{=} \frac { 109.375 t } { \color{Cerulean}{109.375} } \\ 4 & = t \end{aligned}$

Respuesta:

Se necesitan$4$ años para$$2,500$ invertir en$4 \frac{3}{8}$% para ganar$$437.50$ en interés simple.

Ejemplo$\PageIndex{15}$:

Susan invirtió sus ahorros totales de$$12,500$ en dos cuentas ganando intereses simples. Su cuenta de fondos mutuos ganó$7$% el año pasado y su CD obtuvo$4.5$%. Si su interés total para el año era$$670$, ¿cuánto había en cada cuenta?

Solución

La relación entre las dos incógnitas es que suman$$12,500$. Cuando se trata de un total, una técnica común utilizada para evitar dos variables es representar la segunda desconocida como la diferencia del total y la primera desconocida.

Dejar$x$ representar la cantidad invertida en el fondo mutuo.

Dejar$12,500 − x$ representar la cantidad restante invertida en el CD.

Organizar los datos.

Mesa$\PageIndex{7}$
Intereses devengados en el fondo mutuo:	$\begin{aligned} I & = p r t \\ & = x \cdot 0.07 \cdot 1 \\ & = \color{OliveGreen}{0.07 x} \end{aligned}$
Intereses devengados en el CD:	$\begin{aligned} I & = p r t \\ & = ( 12,500 - x ) \cdot 0.045 \cdot 1 \\ & = \color{OliveGreen}{0.045 ( 12,500 - x )} \end{aligned}$
Intereses totales:	$\color{OliveGreen}{$670}$

El interés total es la suma de los intereses obtenidos de cada cuenta.

$\color{Cerulean}{mutual fund interest + CD interest = total interest}$

$ 0.07x + 0.045(12,500−x) = 670$

Esta ecuación modela el problema con una variable. Resolver para$x$.

$\begin{aligned} 0.07 x + 0.045 ( 12,500 - x ) & = 670 \\ 0.07 x + 562.5 - 0.045 x & = 670 \\ 0.025 x + 562.5 & = 670 \\ 0.025 x & = 107.5 \\ x & = \frac { 107.5 } { 0.025 } \\ x & = 4,300 \end{aligned}$

Utilízalo$12,500−x$ para encontrar la cantidad en el CD.

$12,500−x=12,500−\color{OliveGreen}{4,300}\color{Black}{=}8,200$

Respuesta:

Susan invirtió$$4,300$ en$7$% en un fondo mutuo y$$8,200$ en$4.5$% en un CD.

Claves para llevar

Resolver ecuaciones lineales generales implica aislar la variable, con coeficiente$1$, en un lado del signo igual. Para ello, primero use la propiedad de igualdad apropiada de suma o resta para aislar el término variable en un lado del signo igual. A continuación, aísle la variable usando la propiedad de igualdad de multiplicación o división. Por último, verifique que su solución resuelva la ecuación original.
Si resolver una ecuación lineal conduce a una declaración verdadera como$0 = 0$, entonces la ecuación es una identidad y el conjunto de soluciones consiste en todos los números reales,$ℝ$.
Si resolver una ecuación lineal conduce a una declaración falsa como$0 = 5$, entonces la ecuación es una contradicción y no hay solución,$Ø$.
Borrar fracciones multiplicando ambos lados de una ecuación por el múltiplo menos común de todos los denominadores. Distribuir y multiplicar todos los términos por la LCD para obtener una ecuación equivalente con coeficientes enteros.
Simplificar el proceso de resolución de problemas del mundo real mediante la creación de modelos matemáticos que describen la relación entre incógnitas. Usa álgebra para resolver las ecuaciones resultantes.

Ejercicio$\PageIndex{3}$

Determinar si el valor dado es o no una solución.

$−5x + 4 = −1 ; x = −1$
$4x − 3 = −7 ; x = −1$
$3y − 4 = 5; y = \frac{9}{3}$
$−2y + 7 = 12 ; y = −\frac{5}{2}$
$3a − 6 = 18 − a; a = −3$
$5 (2t − 1) = 2 − t; t = 2$
$ax − b = 0; x = \frac{b}{a}$
$ax + b = 2b; x = \frac{b}{a}$

Responder

1. No

3. Sí

5. No

7. Sí

Ejercicio$\PageIndex{4}$

Resolver.

$5x − 3 = 27$
$6x − 7 = 47$
$4x + 13 = 35$
$6x − 9 = 18$
$9a + 10 = 10$
$5 − 3a = 5$
$−8t + 5 = 15$
$−9t + 12 = 33$
$\frac{2}{3} x + \frac{1}{2} = 1$
$\frac{3}{8} x + \frac{5}{4} = \frac{3}{2}$
$\frac{1 − 3y}{5} = 2$
$\frac{2 − 5y}{6} = −8$
$7 − y = 22$
$6 − y = 12$
Resolver para$x: ax − b = c$
Resolver para$x: ax + b = 0$

Responder

1. $6$

3. $\frac{11}{2}$

5. $0$

7. $−\frac{5}{4}$

9. $\frac{3}{4}$

11. $−3$

13. $−15$

15. $x = \frac{b+c}{a}$

Ejercicio$\PageIndex{5}$

Resolver.

$6x − 5 + 2x = 19$
$7 − 2x + 9 = 24$
$12x − 2 − 9x = 5x + 8$
$16 − 3x − 22 = 8 − 4x$
$5y − 6 − 9y = 3 − 2y + 8$
$7 − 9y + 12 = 3y + 11 − 11y$
$3 + 3a − 11 = 5a − 8 − 2a$
$2 − 3a = 5a + 7 − 8a$
$\frac{1}{3} x −\frac{3}{2} + \frac{5}{2} x = \frac{5}{6} x + \frac{1}{4}$
$\frac{5}{8} + \frac{1}{5} x −\frac{3}{4} = \frac{3}{10} x − \frac{1}{4}$
$1.2x − 0.5 − 2.6x = 2 − 2.4x$
$1.59 − 3.87x = 3.48 − 4.1x − 0.51$
$5 − 10x = 2x + 8 − 12x$
$8x − 3 − 3x = 5x − 3$
$5 (y + 2) = 3 (2y − 1) + 10$
$7 (y − 3) = 4 (2y + 1) − 21$
$7 − 5 (3t − 9) = 22$
$10 − 5 (3t + 7) = 20$
$5 − 2x = 4 − 2 (x − 4)$
$2 (4x − 5) + 7x = 5 (3x − 2)$
$4 (4a − 1) = 5 (a − 3) + 2 (a − 2)$
$6 (2b − 1) + 24b = 8 (3b − 1)$
$\frac{2}{3} (x + 18) + 2 = \frac{1}{3} x − 13$
$\frac{2}{5} x − \frac{1}{2} (6x − 3) = \frac{4}{3}$
$1.2 (2x + 1) + 0.6x = 4x$
$6 + 0.5 (7x − 5) = 2.5x + 0.3$
$5 (y + 3) = 15 (y + 1) − 10y$
$3 (4 − y) − 2 (y + 7) = −5y$
$\frac{1}{5} (2a + 3) −\frac{1}{2} = \frac{1}{3} a + \frac{1}{10}$
$\frac{3}{2} a = \frac{3}{4} (1 + 2a) −\frac{1}{5} (a + 5)$
$6 − 3 (7x + 1) = 7 (4 − 3x)$
$6 (x − 6) − 3 (2x − 9) = −9$
$\frac{3}{4} (y − 2) + \frac{2}{3} (2y + 3) = 3$
$\frac{5}{4} − \frac{1}{2} (4y − 3) = \frac{2}{5} (y − 1)$
$−2 (3x + 1) − (x − 3) = −7x + 1$
$6 (2x + 1) − (10x + 9) = 0$
Resolver para$w: P = 2l + 2w$
Resolver para$a: P = a + b + c$
Resolver para$t: D = rt$
Resolver para$w: V = lwh$
Resolver para$b: A = \frac{1}{2} bh$
Resolver para$a:s = \frac{1}{2}at^{2}$
Resolver para$a: A = \frac{1}{2}h (a + b)$
Resolver para$h: V = \frac{1}{3}πr^{2}h$
Resolver para$F: C = \frac{5}{9} (F − 32)$
Resolver para$x: ax + b = c$

Responder

1. $3$

3. $−5$

5. $−\frac{17}{2}$

7. $ℝ$

9. $\frac{7}{8}$

11. $2.5$

13. $Ø$

15. $3$

17. $2$

19. $Ø$

21. $−\frac{5}{3}$

23. $−81$

25. $1.2$

27. $ℝ$

29. $0$

31. $Ø$

33. $\frac{6}{5}$

35. $ℝ$

37. $w = \frac{P − 2l}{2}$

39. $t = \frac{D}{r}$

41. $b = \frac{2A}{h}$

43. $a = \frac{2A}{h} − b$

45. $F = \frac{9}{5} C + 32$

Ejercicio$\PageIndex{6}$

Configura una ecuación algebraica luego resuelve.

Problemas con el número

Cuando$3$ se resta de la suma de un número y$10$ el resultado es$2$. Encuentra el número.
La suma de$3$ veces un número y$12$ es igual a$3$. Encuentra el número.
Tres veces la suma de un número y$6$ es igual a$5$ veces el número. Encuentra el número.
Dos veces la suma de un número y$4$ es igual a$3$ veces la suma del número y$1$. Encuentra el número.
Un entero más grande es$1$ más que$3$ veces otro entero. Si la suma de los enteros es$57$, busque los enteros.
Un entero mayor es$5$ más de dos veces otro entero. Si la suma de los enteros es$83$, busque los enteros.
Un entero es$3$ menos de dos veces otro entero. Encuentra los enteros si su suma es$135$.
Un entero es$10$ menor que$4$ veces otro entero. Encuentra los enteros si su suma es$100$.
La suma de tres enteros consecutivos es$339$. Encuentra los enteros.
La suma de cuatro enteros consecutivos es$130$. Encuentra los enteros.
La suma de tres enteros pares consecutivos es$174$. Encuentra los enteros.
La suma de cuatro enteros pares consecutivos es$116$. Encuentra los enteros.
La suma de tres enteros impares consecutivos es$81$. Encuentra los enteros.
La suma de cuatro enteros impares consecutivos es$176$. Encuentra los enteros.

Responder

1. $−5$

3. $9$

5. $14, 43$

7. $46, 89$

9. $112, 113, 114$

11. $56, 58, 60$

13. $25, 27, 29$

Ejercicio$\PageIndex{7}$

Problemas de geometría

La longitud de un rectángulo es$5$ centímetros menos del doble de su ancho. Si el perímetro es de$134$ centímetros, encuentra el largo y ancho.
La longitud de un rectángulo es$4$ centímetros más que$3$ veces su ancho. Si el perímetro es de$64$ centímetros, encuentra el largo y ancho.
El ancho de un rectángulo es la mitad de su longitud. Si el perímetro mide$36$ pulgadas, encuentra las dimensiones del rectángulo.
El ancho de un rectángulo es$4$ pulgadas menos que su longitud. Si el perímetro mide$72$ pulgadas, encuentra las dimensiones del rectángulo.
El perímetro de un cuadrado es de$48$ pulgadas. Encuentra la longitud de cada lado.
El perímetro de un triángulo equilátero es de$96$ pulgadas. Encuentra la longitud de cada lado.
La circunferencia de un círculo mide$80π$ unidades. Encuentra el radio.
La circunferencia de un círculo mide$25$ centímetros. Encuentra el radio redondeado a la centésima más cercana.

Responder

1. Ancho:$24$ centímetros; largo:$43$ centímetros

3. Ancho:$6$ pulgadas; largo:$12$ pulgadas

5. $12$pulgadas

7. $40$unidades

Ejercicio$\PageIndex{8}$

Problemas de interés simples

¿Por cuántos años$$1,000$ se deben invertir en$5\frac{1}{2}$% para ganar$$165$ en intereses simples?
¿Por cuántos años$$20,000$ se deben invertir en$6\frac{1}{4}$% para ganar$$3,125$ en intereses simples?
¿A qué tasa de interés anual$$6500$ se debe invertir durante$2$ años para rendir$$1,040$ en interés simple?
¿A qué tasa de interés anual$$5,750$ se debe invertir por$1$ año para rendir$$333.50$ en interés simple?
Si el interés simple ganado por$5$ años era$$1,860$ y la tasa de interés anual era$6$%, ¿cuál era el principal?
Si el interés simple ganado por$2$ años era$$543.75$ y la tasa de interés anual era$3\frac{3}{4}$%, ¿cuál era el principal?
¿Cuántos años se tardará en$$600$ duplicar la obtención de intereses simples a una tasa$5$% anual? (Pista: Para duplicar, la inversión debe ganar$$600$ en simple interés.)
¿Cuántos años se tardará en$$10,000$ duplicar la obtención de intereses simples a una tasa$5$% anual? (Pista: Para duplicar, la inversión debe ganar$$10,000$ en simple interés.)
Jim invirtió$$4,200$ en dos cuentas. Una cuenta gana$3$% interés simple y la otra gana$6$%. Si el interés tras$1$ año era$$159$, ¿cuánto invirtió en cada cuenta?
Jane tiene sus$$6,500$ ahorros invertidos en dos cuentas. Ella tiene parte de ello en un CD con$5$% de interés anual y el resto en una cuenta de ahorro que gana$4$% de interés anual. Si el simple interés que se gana de ambas cuentas es$$303$ para el año, entonces ¿cuánto tiene en cada cuenta?
José puso el aguinaldo del año pasado de$$8,400$ en dos cuentas. Invirtió parte en un CD con$2.5$% de interés anual y el resto en un fondo del mercado monetario con$1.5$% de interés anual. Su interés total para el año fue$$198$. ¿Cuánto invirtió en cada cuenta?
Mary invirtió sus ahorros totales de$$3,300$ en dos cuentas. Su cuenta de fondos mutuos ganó$6.2$% el año pasado y su CD obtuvo$2.4$%. Si su interés total para el año era$$124.80$, ¿cuánto había en cada cuenta?
Alice invierte dinero en dos cuentas, una con$3$% de interés anual y otra con$5$% de interés anual. Ella invierte tanto$3$ tiempo en la cuenta de mayor rendimiento como en la cuenta de menor rendimiento. Si su interés total para el año es$$126$, ¿cuánto invirtió en cada cuenta?
James invirtió una herencia en dos bancos separados. Un banco ofreció$5\frac{1}{2}$% de tasa de interés anual y el otro$6\frac{1}{4}$%. Invirtió el doble en la cuenta bancaria de mayor rendimiento que en la otra. Si su interés simple total por$1$ año era$$5,760$, entonces ¿cuál era el monto de su herencia?

Responder

1. $3$años

3. $8$%

5. $$6,200$

7. $20$años

9. Invirtió$$3,100$ en$3$% y$$1,100$ en$6$%.

11. José invirtió$$7,200$ en el CD y$$1,200$ en el fondo del mercado monetario.

13. Alice invirtió$$700$ en$3$% y$$2,100$ en$5$%.

Ejercicio$\PageIndex{9}$

Problemas de movimiento uniforme

Si Jim tarda$1 \frac{1}{4}$ horas en conducir las$40$ millas para trabajar, entonces, ¿cuál es la velocidad promedio de Jim?
Jill tardó$3 \frac{1}{2}$ horas en conducir los$189$ kilómetros a casa desde la universidad. ¿Cuál era su velocidad promedio?
¿A qué velocidad debe conducir Jim si desea recorrer$176$ millas en$2 \frac{3}{4}$ horas?
James y Martin pudieron conducir las$1,140$ millas de Los Ángeles a Seattle. Si el viaje total tardó$19$ horas, entonces ¿cuál era su velocidad promedio?

Responder

1. $32$millas por hora

3. $64$millas por hora

Ejercicio$\PageIndex{10}$

¿Cuál es considerado como el principal negocio del álgebra? Explique.
¿Cuál es el origen de la palabra álgebra?
Crea una identidad o contradicción propia y compártela en el panel de discusión. Proporcione una solución y explique cómo la encontró.
Publica algo que hayas encontrado particularmente útil o interesante en esta sección. Explique por qué.
Realizar una búsqueda en la web para “resolver ecuaciones lineales”. Comparte un enlace al sitio web o video tutorial que creas que es útil.

Responder

1. La respuesta puede variar

3. La respuesta puede variar

5. La respuesta puede variar

Notas al pie

¹²⁹ Declaración que indica que dos expresiones algebraicas son iguales.

¹³⁰ Una ecuación que se puede escribir en la forma estándar$ax + b = 0$, donde$a$ y$b$ son números reales y$a ≠ 0$.

¹³¹ Cualquier valor que pueda reemplazar la variable en una ecuación para producir una declaración verdadera.

¹³² Ecuaciones con el mismo conjunto de soluciones.

¹³³ Propiedades que nos permiten obtener ecuaciones equivalentes sumando, restando, multiplicando y dividiendo ambos lados de una ecuación por números reales no nulos.

¹³⁴ Permite resolver para la variable a cada lado del signo igual, porque$x = 5$ es equivalente a$5 = x$.

¹³⁵ Ecuaciones que son verdaderas para valores particulares.

¹³⁶ Una ecuación que es verdadera para todos los valores posibles.

¹³⁷ Una ecuación que nunca es cierta y que no tiene solución.

Search

Text Color

Text Size

Margin Size

Font Type

Adición propiedad de igualdad:	Si\(A=B\), entonces\(A\color{Cerulean}{+c}\color{Black}{=} B\color{Cerulean}{+c}\)
Resta propiedad de igualdad:	Si\(A=B\), entonces\(A\color{Cerulean}{-c}\color{Black}{-}B\color{Cerulean}{-c}\)
Multiplicación propiedad de igualdad:	Si\(A=B\), entonces\(\color{Cerulean}{c}\color{Black}{A}=\color{Cerulean}{c}\color{Black}{B}\)
División propiedad de igualdad:	Si\(A=B\), entonces\(\frac{A}{\color{Cerulean}{c}}\color{Black}{=}\frac{B}{\color{Cerulean}{c}}\)

Palabras clave	Traducción
Suma, incrementada en, más de, más, sumada a, total	\(+\)
Diferencia, disminuida por, restada de, menos, menos	\(-\)
Producto, multiplicado por, de veces, dos veces	\(\cdot\)
Cociente, dividido por, ratio, per	\(÷\)
Es, total, resultado	\(=\)

Dados intereses para el periodo de tiempo:	\(I=$437.50\)
Dado principal:	\(p=$2,500\)
Tasa dada:	\(r= 4 \frac{3}{8}\)%\(=4.375\)%\(=0.04375\)

Intereses devengados en el fondo mutuo:	\(\begin{aligned} I & = p r t \\ & = x \cdot 0.07 \cdot 1 \\ & = \color{OliveGreen}{0.07 x} \end{aligned}\)
Intereses devengados en el CD:	\(\begin{aligned} I & = p r t \\ & = ( 12,500 - x ) \cdot 0.045 \cdot 1 \\ & = \color{OliveGreen}{0.045 ( 12,500 - x )} \end{aligned}\)
Intereses totales:	\(\color{OliveGreen}{$670}\)