3.4: Resolver sistemas lineales con tres variables

Última actualización
Guardar como PDF

Page ID: 109850

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Verificar soluciones a sistemas lineales con tres variables.
Resolver sistemas lineales con tres variables por eliminación.
Identificar sistemas dependientes e inconsistentes.
Resuelve aplicaciones que involucran tres incógnitas.

Soluciones a Sistemas Lineales con Tres Variables

Las aplicaciones del mundo real a menudo se modelan usando más de una variable y más de una ecuación. En esta sección, estudiaremos sistemas lineales consistentes en tres ecuaciones lineales cada una con tres variables. Por ejemplo,

$\left\{ \begin{array} { l l } { 3 x + 2 y - z = - 7 } & { \color{Cerulean} { (1) } } \\ { 6 x - y + 3 z = - 4 } & { \color{Cerulean} { (2) } } \\ { x + 10 y - 2 z = 2 } & { \color{Cerulean} { (3) } } \end{array} \right.$

Una solución a tal sistema lineal es un triple ¹⁹ ordenado$(x, y, z)$ que resuelve todas las ecuaciones. En este caso,$(−2, 1, 3)$ es la única solución. Para verificar que un triple ordenado es una solución, sustituya los$z$ valores correspondientes$x$$y$ -, -, y -y luego simplifique para ver si obtiene una declaración verdadera de las tres ecuaciones.

Mesa$\PageIndex{1}$
$\color{Cerulean}{Check:}\color{Black}{(-2,1,3)}$
$\begin{array} { r } { \text { Equation } \color{Cerulean}{( 1 ) :} } \\ { 3 x + 2 y + z = - 7 } \\ { 3 ( \color{Cerulean}{- 2}\color{Black}{ )} + 2 ( \color{Cerulean}{1}\color{Black}{ )} - ( \color{Cerulean}{3}\color{Black}{ )} = - 7 } \\ { - 6 + 2 - 3 = - 7 } \\ { - 7 = - 7\:\:\color{Cerulean}{✓} } \end{array}$	$\begin{array} { r } { \text { Equation } \color{Cerulean}{( 2 ) : }} \\ { 6 x -y + 3z = -4 } \\ { 6 ( \color{Cerulean}{- 2}\color{Black}{ )} - (\color{Cerulean}{ 1}\color{Black}{ )} -3 (\color{Cerulean}{ 3}\color{Black}{ )} = - 4 } \\ { - 12 -1 -9 = - 4 } \\ { - 4 = - 4 } \:\:\color{Cerulean}{✓}\end{array}$	$\begin{array} { r } { \text { Equation }\color{Cerulean}{ ( 3 ) :} } \\ { x +10y -2z = 2 } \\ { ( \color{Cerulean}{- 2}\color{Black}{ )} +10 ( \color{Cerulean}{1}\color{Black}{ )} -2 ( \color{Cerulean}{3}\color{Black}{ )} = 2 } \\ { - 2+10 -6 = 2 } \\ { 2 = 2 } \:\:\color{Cerulean}{✓} \end{array}$

Debido a que el triple ordenado satisface las tres ecuaciones concluimos que efectivamente es una solución.

Ejemplo$\PageIndex{1}$:

Determine si$(1, 4, \frac{4}{3}$ es o no una solución al siguiente sistema lineal:

$\left\{ \begin{aligned} 9 x + y - 6 z & = 5 \\ - 6 x - 3 y + 3 z & = - 14 \\ 3 x + 2 y - 7 z & = 15 \end{aligned} \right.$

$\color{Cerulean}{Check:}\color{Black}{(1, 4, \frac{4}{3})}$
$\begin{array} { r } { \text { Equation } \color{Cerulean}{( 1 ) :} } \\ { 9 x + y - 6 z = 5 } \\ { 9 ( \color{Cerulean}{1}\color{Black}{ )} + ( \color{Cerulean}{4}\color{Black}{ )} - 6 \left( \color{Cerulean}{\frac { 4 } { 3 }} \right) = 5 } \\ { 9 + 4 - 8 = 5 } \\ { 5 = 5 } \:\:\color{Cerulean}{✓}\end{array}$	$\begin{array} { r } { \text { Equation } \color{Cerulean}{( 2 ) :} } \\ { -6x -3y +3z = -14 } \\ { 6 ( \color{Cerulean}{1}\color{Black}{ )} - 3( \color{Cerulean}{4}\color{Black}{ )}+ 3 \left( \color{Cerulean}{\frac { 4 } { 3 }} \right) = -14 } \\ { -6-12+4 = -14 } \\ { -14= -14 } \:\:\color{Cerulean}{✓}\end{array}$	$\begin{array} { r } { \text { Equation } \color{Cerulean}{( 3 ) :} } \\ { 3x+2y-7z = 15 } \\ { 3 ( \color{Cerulean}{1}\color{Black}{ )} +2( \color{Cerulean}{4}\color{Black}{ )}-7 \left( \color{Cerulean}{\frac { 4 } { 3 }} \right) = 15 } \\ { 3+8-\frac{28}{3} = 15 } \\ { \frac{5}{3}= 15 } \:\:\color{red}{X}\end{array}$

Responder

El punto no satisface todas las ecuaciones y por lo tanto no es una solución.

Un triple ordenado tal como se$(2, 4, 5)$ puede graficar en el espacio tridimensional de la siguiente manera:

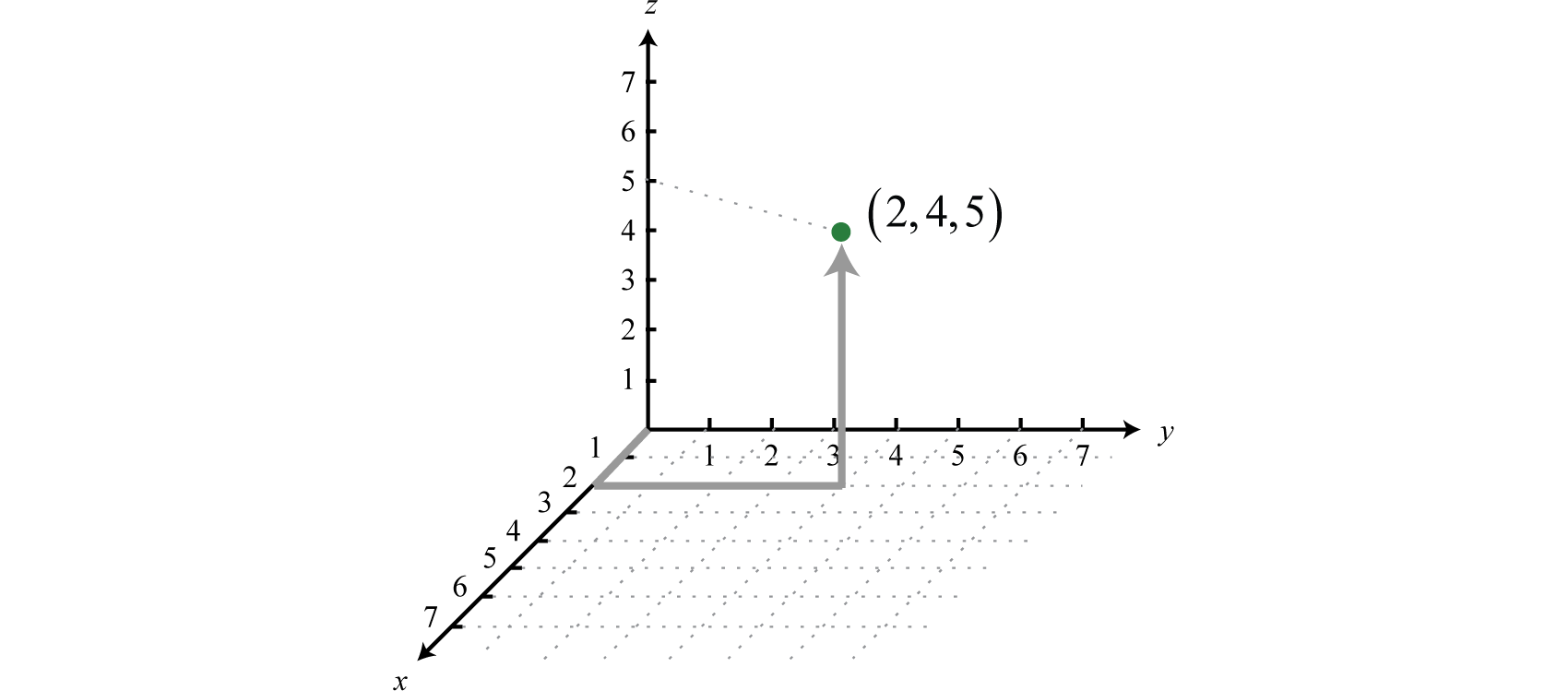
El triple ordenado indica posición relativa al origen$(0, 0, 0)$, en este caso,$2$ unidades a lo largo del$x$ eje,$4$ unidades paralelas al$y$ eje y$5$ unidades paralelas al$z$ eje. Una ecuación lineal con tres variables ²⁰ está en forma estándar si

$ax+by+cz=d$

donde$a, b, c$, y$d$ son números reales. Por ejemplo,$6x + y + 2z = 26$ está en forma estándar. Resolviendo para$z$, obtenemos$z = −3x − \frac{1}{2} y + 13$ y podemos considerar ambas$x$ y$y$ ser las variables independientes. Cuando se grafica en un espacio tridimensional, su gráfica formará una superficie plana recta llamada plano ²¹.

Por lo tanto, la gráfica de un sistema de tres ecuaciones lineales y tres incógnitas constará de tres planos en el espacio. Si hay una solución simultánea, el sistema es consistente y la solución corresponde a un punto donde se cruzan los tres planos.

Graficar planos en el espacio tridimensional no está dentro del alcance de este libro de texto. Sin embargo, siempre es importante entender la interpretación geométrica.

Ejercicio$\PageIndex{1}$

Determinar si es o no$(3, −1, 2)$ una solución al sistema:

$\left\{ \begin{array} { l } { 2 x - 3 y - z = 7 } \\ { 3 x + 5 y - 3 z = - 2 } \\ { 4 x - y + 2 z = 17 } \end{array} \right.$

Contestar

Sí, es una solución.

www.youtube.com/v/2uet4lzxoyg

Resolver sistemas lineales con tres variables por eliminación

En esta sección se utiliza el método de eliminación para resolver sistemas de tres ecuaciones lineales con tres variables. La idea es eliminar una de las variables y resolver el sistema original en un sistema de dos ecuaciones lineales, después de lo cual luego podemos resolver como de costumbre. Los pasos se describen en el siguiente ejemplo.

Ejemplo$\PageIndex{2}$

Resolver:$\left\{ \begin{array} { l l } { 3 x + 2 y - z = - 7 } & { \color{Cerulean}{(1)} } \\ { 6 x - y + 3 z = - 4 } & { \color{Cerulean} { (2) } } \\ { x + 10 y - 2 z = 2 } & { \color{Cerulean} { (3) } } \end{array} \right.$

Solución

Las tres ecuaciones están en forma estándar. De no ser así, sería una buena práctica reescribir las ecuaciones en forma estándar antes de comenzar este proceso.

Paso 1: Elige cualquiera de las dos ecuaciones y elimina una variable. En este caso, podemos alinear la variable$z$ para eliminar si agrupamos$3$ veces la primera ecuación con la segunda ecuación.

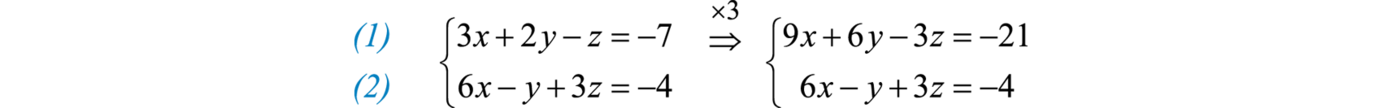
A continuación, sumar las ecuaciones juntas.

$\begin{aligned} 9 x + 6 y \color{red}{- 3 z}&\color{black}{ =} 21 \\ \pm 6 x - y \color{red}{+ 3 z}&\color{black}{ =} - 4 \\ \hline \\ 15x + 5y &= -25 \color{OliveGreen}{✓} \end{aligned}$

Paso 2: Elija otras dos ecuaciones y elimine la misma variable. Podemos alinearnos$z$ para eliminar de nuevo si agrupamos$−2$ veces la primera ecuación con la tercera ecuación.

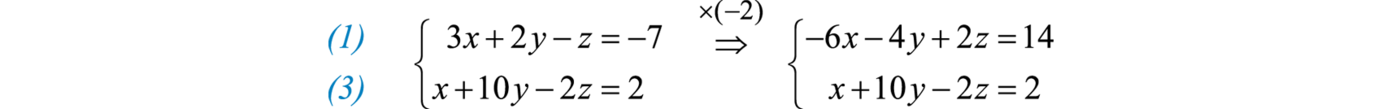
Y luego agregar,

$\begin{aligned} - 6 x - 4 y \color{red}{+ 2 z}&\color{black}{ =} 14 \\ \pm x + 10 y \color{red}{- 2 z} &\color{black}{=} 2 \\ \hline \\-5x + 6y& = 16 \color{OliveGreen}{✓}\end{aligned}$

Paso 3: Resolver el sistema resultante de dos ecuaciones con dos incógnitas. Aquí resolvemos por eliminación. Multiplique la segunda ecuación por$3$ para alinear la variable$x$ a eliminar.

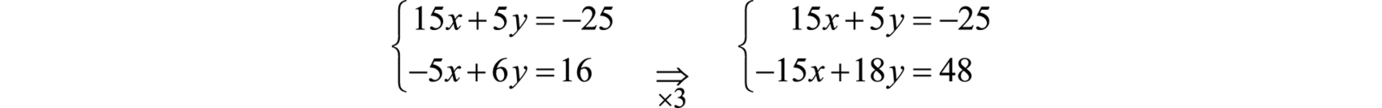
A continuación, sumar las ecuaciones juntas.

$\begin{aligned} \color{red}{15 x}\color{black}{ +} 5 y &= - 25 \\ \pm \color{red}{- 15 x}\color{black}{ +} 18 y &= 48 \\ \hline\\23y&=23\\y&=1 \end{aligned}$

Paso 4: Volver a sustituir y determinar todas las coordenadas. Para encontrar x usa lo siguiente,

$\begin{aligned} 15 x + 5 y & = - 25 \\ 15 x + 5 ( \color{OliveGreen}{1}\color{black}{ )} & = - 25 \\ 15 x & = - 30 \\ x & = - 2 \end{aligned}$

Ahora elige una de las ecuaciones originales para encontrar$z$,

$\begin{aligned} 3 x + 2 y - z & = - 7 \quad\color{Cerulean}{(1)} \\ 3 ( \color{OliveGreen}{- 2}\color{Black}{ )} + 2 ( \color{OliveGreen}{1}\color{Black}{ )} - z & = - 7 \\ - 6 + 2 - z & = - 7 \\ - 4 - z & = - 7 \\ - z & = - 3 \\ z & = 3 \end{aligned}$

De ahí que la solución, presentada como un triple ordenado$(x, y, z)$, sea$(−2, 1, 3)$. Este es el mismo sistema que comprobamos al inicio de esta sección.

Responder

$(-2,1,3)$

No importa qué variable escojamos eliminar inicialmente, siempre y cuando la eliminemos dos veces con dos conjuntos diferentes de ecuaciones.

Ejemplo$\PageIndex{3}$

Resolver:$\left\{ \begin{array} { c } { - 6 x - 3 y + 3 z = - 14 } \\ { 9 x + y - 6 z = 5 } \\ { 3 x + 2 y - 7 z = 15 } \end{array} \right.$.

Solución

Debido a que$y$ tiene coeficiente$1$ en la segunda ecuación, elija eliminar esta variable. Usar ecuaciones$1$ y$2$ eliminar$y$.

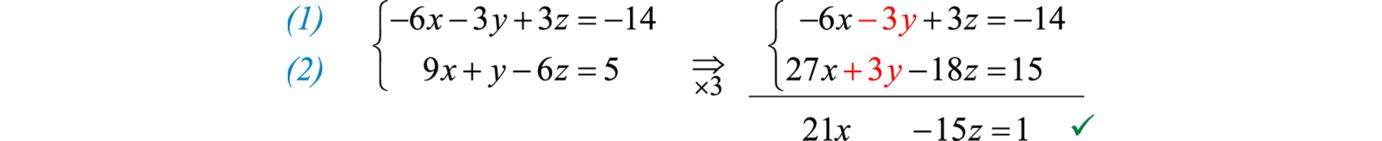
A continuación usa las ecuaciones$2$ y$3$ para eliminar de$y$ nuevo.

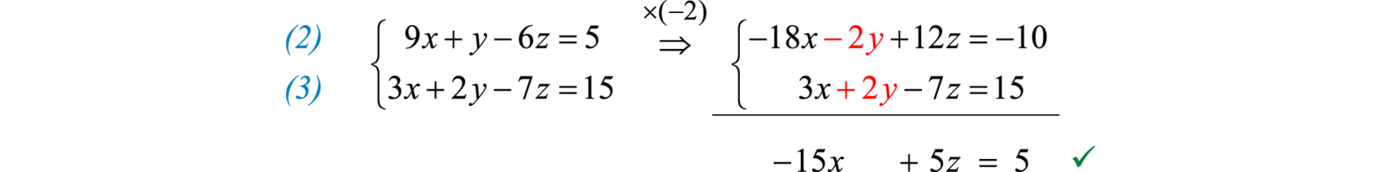
Esto deja un sistema de dos ecuaciones con dos variables$x$ y$z$,

$\left\{ \begin{array} { l } { 21 x - 15 z = 1 } \\ { - 15 x + 5 z = 5 } \end{array} \right.$

Multiplique la segunda ecuación por$3$ y elimine la variable$z$.

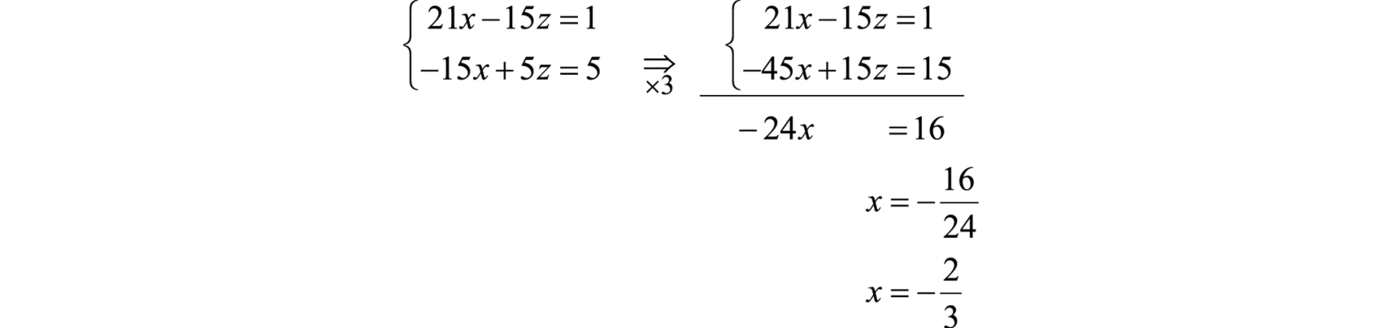
Ahora vuelve sustituto para encontrar$z$.

$\begin{aligned} 21 x - 15 z & = 1 \\ 21 \left( \color{Cerulean}{- \frac { 2 } { 3} } \right) - 15 z & = 1 \\ - 14 - 15 z & = 1 \\ - 15 z & = 15 \\ z & = - 1 \end{aligned}$

Por último, elige una de las ecuaciones originales para encontrar$y$.

$\begin{aligned} - 6 x - 3 y + 3 z & = - 14 \\ - 6 \left( \color{Cerulean}{- \frac { 2 } { 3} } \right) - 3 y + 3 ( \color{Cerulean}{- 1}\color{Black}{ )} & = - 14 \\ 4 - 3 y - 3 & = - 14 \\ 1 - 3 y & = - 14 \\ - 3 y & = - 15 \\ y & = 5 \end{aligned}$

Contestar

$\left( - \frac { 2 } { 3 } , 5 , - 1 \right)$

Ejemplo$\PageIndex{4}$

Resolver:$\left\{ \begin{array} { l } { 2 x + 6 y + 7 z = 4 } \\ { - 3 x - 4 y + 5 z = 12 } \\ { 5 x + 10 y - 3 z = - 13 } \end{array} \right.$.

Solución

En este ejemplo, no hay elección obvia de variable a eliminar. Elegimos eliminar$x$.

$\begin{array} { l } { \color{Cerulean}{ (1) } } \\ { \color{Cerulean}{ (2) } } \end{array}$$\left \{ \begin{array} { l l } { 2 x + 6y + 7z = 4 } & { \stackrel{ \times3 } { \Rightarrow } } \\ { -3 x -4y +5z = 12 } & { \underset { \times 2 } { \Rightarrow }} \end{array} \right. \left\{ \begin{array} { l } { 6 x + 18 y + 21z = 12 } \\ { -6x -8y +10z = 24 } \end{array} \\\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad10y + 31z=36 \color{OliveGreen}{✓} \right.$

Siguiente usa ecuaciones$2$ y$3$ para eliminar de$x$ nuevo.

$\begin{array} { l } { \color{Cerulean}{ (2) } } \\ { \color{Cerulean}{ (3) } } \end{array}$$\left \{ \begin{array} { l l } { -3 x -4y + 5z = 12 } & { \stackrel{ \times5 } { \Rightarrow } } \\ { 5 x +10y -3z = -13 } & { \underset { \times 3 } { \Rightarrow }} \end{array} \right. \left\{ \begin{array} { l } { -15 x -20 y + 25z = 60 } \\ { 15x +30y -9z = -39 }\end{array} \\\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad10y + 16z=21 \color{OliveGreen}{✓} \right.$

Esto deja un sistema de dos ecuaciones con dos variables$y$ y$z$,

$\left\{ \begin{array} { l } { 10 y + 31 z = 36 } \\ { 10 y + 16 z = 21 } \end{array} \right.$

Multiplique la primera ecuación por$−1$ como medio para eliminar la variable$y$.

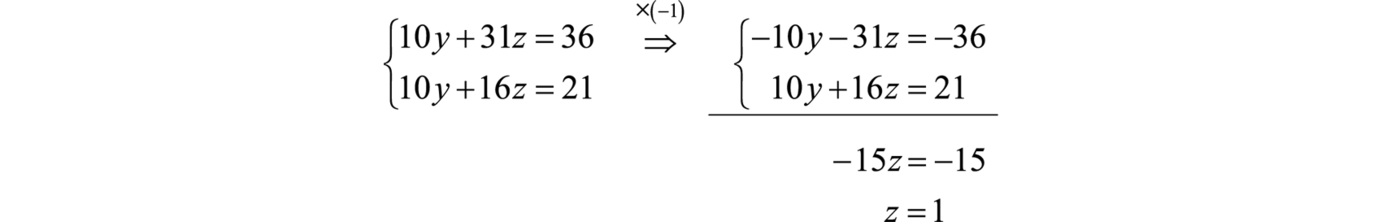
Ahora vuelve sustituto para encontrar$y$.

$\begin{aligned} 10 y + 31 z & = 36 \\ 10 y + 31 ( \color{OliveGreen}{1}\color{Black}{ )} & = 36 \\ 10 y + 31 & = 36 \\ 10 y & = 5 \\ y & = \frac { 5 } { 10 } \\ y & = \frac { 1 } { 2 } \end{aligned}$

Elige cualquiera de las ecuaciones originales para encontrar$x$.

$\begin{aligned} 2 x + 6 y + 7 z & = 4 \\ 2 x + 6 \left( \color{OliveGreen}{\frac { 1 } { 2 }} \right) + 7 ( \color{OliveGreen}{1}\color{Black}{ )} & = 4 \\ 2 x + 3 + 7 & = 4 \\ 2 x + 10 & = 4 \\ 2 x & = - 6 \\ x & = - 3 \end{aligned}$

Responder

$\left( - 3 , \frac { 1 } { 2 } , 1 \right)$

Ejercicio$\PageIndex{2}$

Resolver:$\left\{ \begin{array} { l } { 2 x - 3 y - z = 7 } \\ { 3 x + 5 y - 3 z = - 2 } \\ { 4 x - y + 2 z = 17 } \end{array} \right.$

Contestar

$(3, -1, 2)$

www.youtube.com/v/cjsv8d3g2ic

Sistemas Dependientes e Inconsistentes

Al igual que con los sistemas lineales con dos variables, no todos los sistemas lineales con tres variables tienen una sola solución. A veces no hay soluciones simultáneas.

Ejemplo$\PageIndex{5}$:

Resuelve el sistema:$\left\{ \begin{aligned} 4 x - y + 3 z & = 5 \\ 21 x - 4 y + 18 z & = 7 \\ - 9 x + y - 9 z & = - 8 \end{aligned} \right.$.

Solución

En este caso optamos por eliminar la variable$y$.

$\begin{array} { l } { \color{Cerulean}{ (1) } } \\ { \color{Cerulean}{ (3) } } \end{array}$$\left \{ \begin{array} { l l } { 4 x -y + 3z = 5 } & \\ { -9 x +y -9z = -8 } & \end{array} \right. \\\quad-5x -6z=-3 \color{OliveGreen}{✓} $

Siguiente usa ecuaciones$2$ y$3$ para eliminar de$y$ nuevo.

Esto deja un sistema de dos ecuaciones con dos variables$x$ y$z$,

$\left\{ \begin{array} { l } { - 5 x - 6 z = - 3 } \\ { - 15 x - 18 z = - 25 } \end{array} \right.$

Multiplica la primera ecuación por$-3$ y elimina la variable$z$.

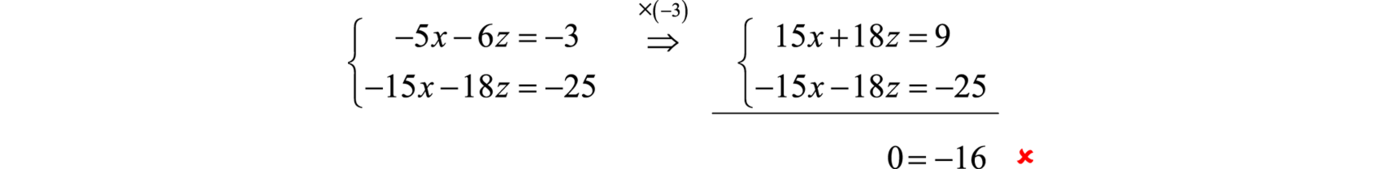
Sumar las ecuaciones resultantes juntas conduce a una declaración falsa, lo que indica que el sistema es inconsistente. No hay solución simultánea.

Responder

$\varnothing$

Al igual que con los sistemas lineales con dos variables, algunos sistemas lineales con tres variables tienen infinitamente muchas soluciones. Tales sistemas se denominan sistemas dependientes.

Ejemplo$\PageIndex{6}$

Resuelve el sistema:$\left\{ \begin{array} { c } { 7 x - 4 y + z = - 15 } \\ { 3 x + 2 y - z = - 5 } \\ { 5 x + 12 y - 5 z = - 5 } \end{array} \right.$.

Solución

Elimine$z$ sumando la primera y la segunda ecuaciones juntas.

$\begin{array} { l } { \color{Cerulean}{ (1) } } \\ { \color{Cerulean}{ (3) } } \end{array}$$\left \{ \begin{array} { l l } { 7 x -4y + z = -15 } & \\ { 3 x +2y -z = -5 } & \end{array} \right. \\\quad10x -2y=-20 \color{OliveGreen}{✓} $

Siguiente usa ecuaciones$1$ y$3$ para eliminar de$z$ nuevo.

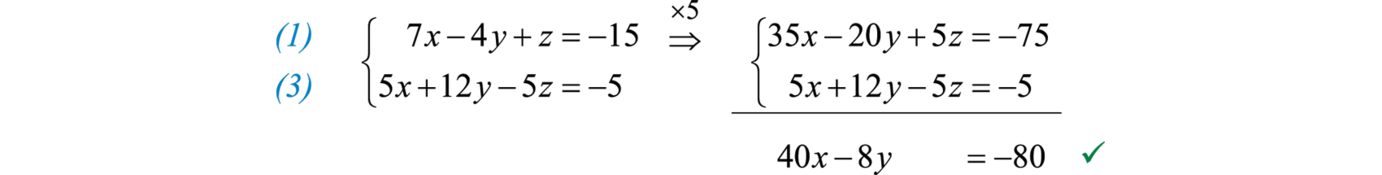
Esto deja un sistema de dos ecuaciones con dos variables$x$ y$y$,

$\left\{ \begin{array} { l } { 10 x - 2 y = - 20 } \\ { 40 x - 8 y = - 80 } \end{array} \right.$

Alinee la variable$y$ a eliminar dividiendo la primera ecuación por$2$ y la segunda ecuación por$−8$.

$\left \{ \begin{array} { l l } { 10 x -2y = -20 } & { \stackrel{ \div 2} { \Longrightarrow } } \\ { 40 x -8y = -80 } & { \underset { \div (-8) } { \Longrightarrow }} \end{array} \right. \left\{ \begin{array} { l } { 5 x - y = -10 } \\ { -5x +y = 10 }\end{array} \\\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad 0=0 \:\:\color{Cerulean}{True} \right.$

Una afirmación verdadera indica que el sistema es dependiente. Para expresar el número infinito de soluciones$(x, y,z)$ en términos de una variable, resolvemos para$y$ y$z$ ambas en términos de$x$.

$\begin{aligned} 10 x - 2 y & = - 20 \\ - 2 y & = - 10 x - 20 \\ \frac { - 2 y } { - 2 } & = \frac { - 10 x - 20 } { - 2 } \\ y & = 5 x + 10 \end{aligned}$

Una vez que tenemos$y$ en términos de$x$, podemos resolver para$z$ en términos de$x$ por volver a sustituir en una de las ecuaciones originales.

$\begin{aligned} 7 x - 4 y + z & = - 15 \\ 7 x - 4 ( \color{OliveGreen}{5 x + 10}\color{black}{ )} + z & = - 15 \\ 7 x - 20 x - 40 + z & = - 15 \\ - 13 x - 40 + z & = - 15 \\ z & = 13 x + 25 \end{aligned}$

Responder

$( x , 5 x + 10,13 x + 25 )$

Un sistema consistente con infinitamente muchas soluciones es un sistema dependiente. Dados tres planos, infinitamente muchas soluciones simultáneas pueden ocurrir de varias maneras.

Ejercicio$\PageIndex{3}$

Resolver:$\left\{ \begin{aligned} 7 x + y - 2 z & = - 4 \\ - 21 x - 7 y + 8 z & = 4 \\ 7 x + 3 y - 3 z & = 0 \end{aligned} \right.$

Contestar

$\left( x , \frac { 7 } { 3 } x + 4 , \frac { 14 } { 3 } x + 4 \right)$

www.youtube.com/v/wggatnijmli

Aplicaciones que involucran tres incógnitas

Muchas aplicaciones del mundo real involucran más de dos incógnitas. Cuando una aplicación requiere tres variables, buscamos relaciones entre las variables que nos permitan escribir tres ecuaciones.

Ejemplo$\PageIndex{7}$

Un teatro comunitario vendió$63$ boletos para la actuación de la tarde por un total de$$444$. Un costo de boleto de adulto$$8$, un costo$$4$ de boleto para niños y un costo de boleto para adultos mayores$$6$. Si se vendieron dos veces más boletos a adultos que a niños y adultos mayores combinados, ¿cuántos de cada boleto se vendieron?

Solución

Comience por identificar tres variables.

Dejar$x$ representar el número de boletos para adultos vendidos.

Dejar$y$ representar el número de boletos infantiles vendidos.

Dejar$z$ representar el número de boletos senior vendidos.

La primera ecuación proviene de la afirmación de que se vendieron$63$ boletos.

$\color{Cerulean}{(1)}\quad \color{black}{x}+y+z=63$

La segunda ecuación proviene de la venta total de boletos.

$\color{Cerulean}{(2)}\quad \color{black}{8}x+4y+6z=444$

La tercera ecuación proviene de la afirmación de que se vendieron el doble de boletos para adultos que los boletos infantiles y senior combinados.

$\begin{aligned} x & = 2 ( y + z ) \\ x & = 2 y + 2 z \\ \color{Cerulean}{( 3 )} \quad\color{black}{ x} - 2 y - 2 z & = 0 \end{aligned}$

Por lo tanto, el problema es modelado por el siguiente sistema lineal.

$\left\{ \begin{array} { c } { x + y + z = 63 } \\ { 8 x + 4 y + 6 z = 444 } \\ { x - 2 y - 2 z = 0 } \end{array} \right.$

Resolver este sistema se deja como un ejercicio. La solución es$(42, 9, 12)$.

Responder

El teatro vendió boletos$42$ para adultos, boletos para$9$ niños y boletos$12$ para adultos mayores.

Claves para llevar

Una solución simultánea a un sistema lineal con tres ecuaciones y tres variables es un triple ordenado$(x, y, z)$ que satisface todas las ecuaciones. Si no resuelve cada ecuación, entonces no es una solución.
Podemos resolver sistemas de tres ecuaciones lineales con tres incógnitas por eliminación. Elija cualquiera de las dos ecuaciones y elimine una variable. A continuación, elija otras dos ecuaciones y elimine la misma variable. Esto dará como resultado un sistema de dos ecuaciones con dos variables que pueden ser resueltas por cualquier método aprendido previamente.
Si el proceso de resolver un sistema conduce a una declaración falsa, entonces el sistema es inconsistente y no tiene solución.
Si el proceso de resolver un sistema conduce a una afirmación verdadera, entonces el sistema es dependiente y tiene infinitamente muchas soluciones.
Para resolver aplicaciones que requieran tres variables, busque relaciones entre las variables que le permitan escribir tres ecuaciones lineales.

Ejercicio$\PageIndex{4}$

Determinar si el triple ordenado dado es o no una solución al sistema dado.

1. $(3, -2, -1)$;

$\left\{ \begin{array} { c } { x + y - z = 2 } \\ { 2 x - 3 y + 2 z = 10 } \\ { x + 2 y + z = - 3 } \end{array} \right.$

2. $(-8, -1, 5)$;

$\left\{ \begin{array} { c } { x + 2 y - z = - 15 } \\ { 2 x - 6 y + 2 z = 0 } \\ { 3 x - 9 y + 4 z = 5 } \end{array} \right.$

3. $(1, -9, 2)$;

$ \left\{ \begin{array} { c } { 8 x + y - z = - 3 } \\ { 7 x - 2 y - 3 z = 19 } \\ { x - y + 9 z = 28 } \end{array} \right.$

4. $(-4, 1, -3)$;

$\left\{ \begin{array} { l } { 3 x + 2 y - z = - 7 } \\ { x - 5 y + 2 z = 3 } \\ { 2 x + y + 3 z = - 16 } \end{array} \right.$

5. $\left( 6 , \frac { 2 } { 3 } , - \frac { 1 } { 2 } \right)$;

$\left\{ \begin{array} { c } { x + 6 y - 4 z = 12 } \\ { - x + 3 y - 2 z = - 3 } \\ { x - 9 y + 8 z = - 4 } \end{array} \right.$

6. $\left( \frac { 1 } { 4 } , - 1 , - \frac { 3 } { 4 } \right)$;

$\left\{ \begin{array} { r } { 2 x - y - 2 z = 3 } \\ { 4 x + 5 y - 8 z = 2 } \\ { x - 2 y - z = 3 } \end{array} \right.$

7. $(3, -2, 1)$;

$\left\{ \begin{array} { c } { 4 x - 5 y = 22 } \\ { 2 y - z = 8 } \\ { - 5 x + 2 z = - 13 } \end{array} \right.$

8. $\left( 1 , \frac { 5 } { 2 } , - \frac { 1 } { 2 } \right)$;

$\left\{ \begin{aligned} 2 y - 6 z & = 8 \\ 3 x - 4 z & = 5 \\ 18 z & = - 9 \end{aligned} \right.$

9. $\left( \frac { 1 } { 2 } , - 2,6 \right)$;

$\left\{ \begin{array} { c } { a - b + c = 9 } \\ { 4 a - 2 b + c = 14 } \\ { 2 a + b + \frac { 1 } { 2 } c = 3 } \end{array} \right.$

10. $( - 1,5 , - 7 )$;

$\left\{ \begin{array} { l } { 3 a + b + \frac { 1 } { 3 } c = - \frac { 1 } { 3 } } \\ { 8 a + 2 b + \frac { 1 } { 2 } c = - \frac { 3 } { 2 } } \\ { 25 a + 5 b + c = - 7 } \end{array} \right.$

Contestar

1. No

3. Sí

5. Sí

7. No

9. No

Ejercicio$\PageIndex{5}$

Resolver

$\left\{ \begin{array} { l } { 2 x - 3 y + z = 4 } \\ { 5 x + 2 y + 2 z = 2 } \\ { x + 4 y - 3 z = 7 } \end{array} \right.$
$\left\{ \begin{array} { c } { 5 x - 2 y + z = - 9 } \\ { 2 x + y - 3 z = - 5 } \\ { 7 x + 3 y + 2 z = 6 } \end{array} \right.$
$\left\{ \begin{array} { c } { x + 5 y - 2 z = 15 } \\ { 3 x - 7 y + 4 z = - 7 } \\ { 2 x + 4 y - 3 z = 21 } \end{array} \right.$
$\left\{ \begin{array} { c } { x - 4 y + 2 z = 3 } \\ { 2 x + 3 y - 3 z = 9 } \\ { 3 x + 2 y + 4 z = - 1 } \end{array} \right.$
$\left\{ \begin{array} { c } { 5 x + 4 y - 2 z = - 5 } \\ { 4 x - y + 3 z = 14 } \\ { 6 x + 3 y - 5 z = - 12 } \end{array} \right.$
$\left\{ \begin{array} { c } { 2 x + 3 y - 2 z = - 4 } \\ { 3 x + 5 y + 3 z = 17 } \\ { 2 x + y - 4 z = - 8 } \end{array} \right.$
$\left\{ \begin{array} { c } { x + y - 4 z = 1 } \\ { 9 x - 3 y + 6 z = 2 } \\ { - 6 x + 2 y - 4 z = - 2 } \end{array} \right.$
$\left\{ \begin{aligned} 5 x - 8 y + z & = 5 \\ - 3 x + 5 y - z & = - 3 \\ - 11 x + 18 y - 3 z & = - 5 \end{aligned} \right.$
$\left\{ \begin{aligned} x - y + 2 z & = 3 \\ 2 x - y + 3 z & = 2 \\ - x - 3 y + 4 z & = 1 \end{aligned} \right.$
$\left\{ \begin{array} { c } { x + y + z = 8 } \\ { x - y + 4 z = - 7 } \\ { - x - y + 2 z = 1 } \end{array} \right.$
$\left\{ \begin{array} { l } { 4 x - y + 2 z = 3 } \\ { 6 x + 3 y - 4 z = - 1 } \\ { 3 x - 2 y + 3 z = 4 } \end{array} \right.$
$\left\{ \begin{array} { c } { x - 4 y + 6 z = - 1 } \\ { 3 x + 8 y - 2 z = 2 } \\ { 5 x + 2 y - 3 z = - 5 } \end{array} \right.$
$\left\{ \begin{array} { l } { 3 x - 4 y - z = 7 } \\ { 5 x - 8 y + 3 z = 11 } \\ { 2 x + 6 y + z = 9 } \end{array} \right.$
$\left\{ \begin{array} { l } { 3 x + y - 4 z = 6 } \\ { 6 x - 5 y + 3 z = 1 } \\ { 9 x + 3 y - 4 z = 10 } \end{array} \right.$
$\left\{ \begin{array} { l } { 7 x - 6 y + z = 8 } \\ { - x + 2 y - z = 4 } \\ { x + 2 y - 2 z = 14 } \end{array} \right.$
$\left\{ \begin{array} { l } { - 9 x + 3 y + z = 3 } \\ { 12 x - 4 y - z = 2 } \\ { - 6 x + 2 y + z = 8 } \end{array} \right.$
$\left\{ \begin{array} { c } { a - b + c = 9 } \\ { 4 a - 2 b + c = 14 } \\ { 2 a + b + \frac { 1 } { 2 } c = 3 } \end{array} \right.$
$\left\{ \begin{array} { l } { 3 a + b + \frac { 1 } { 3 } c = - \frac { 1 } { 3 } } \\ { 8 a + 2 b + \frac { 1 } { 2 } c = - \frac { 3 } { 2 } } \\ { 25 a + 5 b + c = - 7 } \end{array} \right.$
$\left\{ \begin{array} { l } { 3 x - 5 y - 4 z = - 5 } \\ { 4 x - 6 y + 3 z = - 22 } \\ { 6 x + 8 y - 5 z = 20 } \end{array} \right.$
$\left\{ \begin{array} { l } { 7 x + 4 y - 2 z = 8 } \\ { 2 x + 2 y + 3 z = - 4 } \\ { 3 x - 6 y - 7 z = 8 } \end{array} \right.$
$\left\{ \begin{array} { c } { 9 x + 7 y + 4 z = 8 } \\ { 4 x - 5 y - 6 z = - 11 } \\ { - 5 x + 2 y + 3 z = 4 } \end{array} \right.$
$\left\{ \begin{array} { l } { 3 x + 7 y + 2 z = - 7 } \\ { 5 x + 4 y + 3 z = 5 } \\ { 2 x - 3 y + 5 z = - 4 } \end{array} \right.$
$\left\{ \begin{array} { l } { 4 x - 3 y = 1 } \\ { 2 y - 3 z = 2 } \\ { 3 x + 2 z = 3 } \end{array} \right.$
$\left\{ \begin{array} { l } { 5 y - 3 z = - 28 } \\ { 3 x + 2 y = 8 } \\ { 4 y - 7 z = - 27 } \end{array} \right.$
$\left\{ \begin{aligned} 2 x + 3 y + z & = 1 \\ 6 y + z & = 4 \\ 2 z & = - 4 \end{aligned} \right.$
$\left\{ \begin{aligned} x - 3 y - 2 z & = 5 \\ 2 y + 6 z & = - 1 \\ 4 z & = - 6 \end{aligned} \right.$
$\left\{ \begin{aligned} 2 x & = 10 \\ 6 x - 5 y & = 30 \\ 3 x - 4 y - 2 z & = 3 \end{aligned} \right.$
$\left\{ \begin{array} { c } { 2 x + 7 z = 2 } \\ { - 4 y = 6 } \\ { 8 y + 3 z = 0 } \end{array} \right.$
$\left\{ \begin{array} { c } { 5 x + 7 y + 2 z = 4 } \\ { 12 x + 16 y + 4 z = 15 } \\ { 10 x + 13 y + 3 z = 14 } \end{array} \right.$
$\left\{ \begin{array} { l } { 8 x + 12 y - 8 z = 5 } \\ { 2 x + 3 y - 2 z = 2 } \\ { 4 x - 2 y + 5 z = - 1 } \end{array} \right.$
$\left\{ \begin{array} { c } { 17 x - 4 y - 3 z = - 2 } \\ { 5 x + \frac { 1 } { 2 } y - 2 z = - \frac { 9 } { 2 } } \\ { 2 x + 5 y - 4 z = - 13 } \end{array} \right.$
$\left\{ \begin{aligned} 3 x - 5 y - \frac { 1 } { 2 } z & = \frac { 7 } { 2 } \\ x - y - \frac { 1 } { 2 } z & = - \frac { 1 } { 2 } \\ 3 x - 8 y + z & = 11 \end{aligned} \right.$
$\left\{ \begin{array} { l } { 4 a - 2 b + 3 c = 9 } \\ { 3 a + 3 b - 5 c = - 6 } \\ { 10 a - 6 b + 5 c = 13 } \end{array} \right.$
$\left\{ \begin{array} { l } { 6 a - 2 b + 5 c = - 2 } \\ { 4 a + 3 b - 3 c = - 1 } \\ { 3 a + 5 b + 6 c = 24 } \end{array} \right.$

Contestar

1. $(2, -1, -3)$

3. $(4, 1, -3)$

5. $(1, -1, 3)$

7. $\varnothing$

9. $(5, -10, -6)$

11. $\left( \frac { 1 } { 2 } , - 2 , - \frac { 1 } { 2 } \right)$

13. $\left( 3 , \frac { 1 } { 2 } , 0 \right)$

15. $\left( x , \frac { 3 } { 2 } x - 3,2 x - 10 \right)$

17. $(1, -2, 6)$

19. $(-1, 2, -2)$

21. $(1, -3, 5)$

23. $(1, 1, 0)$

25. $(0, 1, -2)$

27. $(5, 0, 6)$

29. $\varnothing$

31. $( x , 2 x - 1,3 x + 2 )$

33. $(1, 2, 3)$

Ejercicio$\PageIndex{6}$

Configura un sistema de ecuaciones y úsalo para resolver lo siguiente.

La suma de tres enteros es$38$. Dos$4$ veces menos que el número entero menor es igual a la suma de los otros. La suma del número entero menor y mayor es igual a$2$ más del doble de la del otro. Encuentra los enteros.
La suma de tres enteros es$40$. Tres veces el entero más pequeño es igual a la suma de los otros. Dos veces más grande es igual a$8$ más que la suma de los demás. Encuentra los enteros.
La suma de los ángulos$A, B$, y$C$ de un triángulo es$180°$. El ángulo mayor$C$ es igual al doble de la suma de los otros dos. Cuatro veces el ángulo más pequeño$A$ es igual a la diferencia de ángulo$C$ y$B$. Encuentra los ángulos.
La suma de los ángulos$A, B$, y$C$ de un triángulo es$180°$. $C$El ángulo es igual a la suma de los otros dos ángulos. Cinco veces el ángulo$A$ es igual a la suma de ángulo$C$ y$B$. Encuentra los ángulos.
Se$$12,000$ invirtió un total en tres cuentas de ganancia de intereses. Las tasas de interés fueron$2$$4$%,% y$5$%. Si el interés simple total de un año fue$$400$ y el monto invertido en$2$% era igual a la suma de los montos en las otras dos cuentas, entonces ¿cuánto se invirtió en cada cuenta?
Joe invirtió su$$6,000$ bono en tres cuentas ganando$4 \frac{1}{2}$% de interés. Invirtió el doble en la cuenta ganando$4 \frac{1}{2}$% que en las otras dos cuentas combinadas. Si el interés simple total del año fue$$234$, ¿cuánto invirtió Joe en cada cuenta?
Un frasco contiene monedas de cinco centavos, monedas de diez centavos y cuartos. Hay$105$ monedas con un valor total de$$8.40$. Si hay$3$ más del doble de monedas de diez centavos que cuartos, encuentra cuántas de cada moneda hay en el frasco.
Un billfold tiene un dólar, cinco dólares, y billetes de diez dólares y tiene un valor de$$210$. Hay$50$ billetes totales donde el número de billetes de un dólar es uno menos del doble del número de billetes de cinco dólares. ¿Cuántos de cada factura hay?
Una enfermera desea preparar una solución antiséptica tópica de$15$ -onza que contenga$3$% de peróxido de hidrógeno. Para obtener esta mezcla, se agrega agua purificada a los productos$1.5$% y$10$% de peróxido de hidrógeno existentes. Si solo se dispone de$3$ onzas de la solución de$10$% de peróxido de hidrógeno, ¿cuánto de la solución de$1.5$% de peróxido de hidrógeno y agua se necesita?
Un químico necesita producir una solución de$32$ -onza que consiste en$8 \frac{3}{4}$% de ácido. Tiene tres concentrados con$5$%,$10$% y$40$% de ácido. Si va a usar el doble de la solución$5$% ácida que la solución$10$%, entonces ¿cuántas onzas de la solución$40$% necesitará?
Un teatro comunitario vendió$128$ boletos para la actuación nocturna por un total de$$1,132$. Un costo de boleto de adulto$$10$, un costo$$5$ de boleto para niños y un costo de boleto para adultos mayores$$6$. Si se vendieron tres veces más boletos a adultos que a niños y adultos mayores combinados, ¿cuántos de cada boleto se vendieron?
James vendió$82$ artículos en la reunión de intercambio por un total de$$504$. Vendió paquetes de calcetines para$$6$, camisetas estampadas para$$12$, y sombreros para$$5$. Si vendía$5$ veces tantos sombreros como playeras, ¿cuántos de cada artículo vendió?
Una parábola pasa por tres puntos$(−1, 7), (1, −1)$ y$(2, −2)$. Utilizar estos puntos y$y = a x ^ { 2 } + b x + c$ construir un sistema de tres ecuaciones lineales en términos de$a, b$,$c$ y luego resolver el sistema.
Una parábola pasa por tres puntos$(−2, 11), (−1, 4)$ y$(1, 2)$. Utilizar estos puntos y$y = a x ^ { 2 } + b x + c$ construir un sistema de tres ecuaciones lineales en términos de$a, b$,$c$ y resolverlo.

Contestar

1. $8, 12, 18$

3. $A = 20 ^ { \circ } , B = 40 ^ { \circ } , \text { and } C = 120 ^ { \circ }$

5. El monto invertido en$2$% fue$$6,000$, el monto invertido en$4$% fue$$2,000$, y el monto invertido en$5$% fue$$4,000$.

7. $72$níqueles, monedas de$23$ diez centavos y$10$ cuartos

9. $10$onzas de la solución$1.5$% de peróxido de hidrógeno y$2$ onzas de agua

11. $96$Se vendieron boletos para adultos, boletos$20$ infantiles y boletos para$12$ personas mayores.

13. $a = 1, b = −4$, y$c = 2$

Ejercicio$\PageIndex{7}$

En una tarjeta de nota, anote los pasos para resolver un sistema de tres ecuaciones lineales con tres variables usando eliminación. Usa tus notas para explicarle a un amigo cómo resolver uno de los ejercicios de esta sección.
Investigar y discutir el ajuste de curvas. ¿Por qué el ajuste de curvas es un tema importante?

Contestar: 1. La respuesta puede variar

Notas al pie

¹⁹ Triples$(x, y, z)$ que identifican la posición relativa al origen en el espacio tridimensional.

²⁰ Una ecuación que se puede escribir en la forma estándar$ax + by + cz = d$ donde$a, b, c$, y$d$ son números reales.

²¹ Cualquier superficie plana bidimensional.

\(\color{Cerulean}{Check:}\color{Black}{(-2,1,3)}\)
\(\begin{array} { r } { \text { Equation } \color{Cerulean}{( 1 ) :} } \\ { 3 x + 2 y + z = - 7 } \\ { 3 ( \color{Cerulean}{- 2}\color{Black}{ )} + 2 ( \color{Cerulean}{1}\color{Black}{ )} - ( \color{Cerulean}{3}\color{Black}{ )} = - 7 } \\ { - 6 + 2 - 3 = - 7 } \\ { - 7 = - 7\:\:\color{Cerulean}{✓} } \end{array}\)	\(\begin{array} { r } { \text { Equation } \color{Cerulean}{( 2 ) : }} \\ { 6 x -y + 3z = -4 } \\ { 6 ( \color{Cerulean}{- 2}\color{Black}{ )} - (\color{Cerulean}{ 1}\color{Black}{ )} -3 (\color{Cerulean}{ 3}\color{Black}{ )} = - 4 } \\ { - 12 -1 -9 = - 4 } \\ { - 4 = - 4 } \:\:\color{Cerulean}{✓}\end{array}\)	\(\begin{array} { r } { \text { Equation }\color{Cerulean}{ ( 3 ) :} } \\ { x +10y -2z = 2 } \\ { ( \color{Cerulean}{- 2}\color{Black}{ )} +10 ( \color{Cerulean}{1}\color{Black}{ )} -2 ( \color{Cerulean}{3}\color{Black}{ )} = 2 } \\ { - 2+10 -6 = 2 } \\ { 2 = 2 } \:\:\color{Cerulean}{✓} \end{array}\)

\(\color{Cerulean}{Check:}\color{Black}{(1, 4, \frac{4}{3})}\)
\(\begin{array} { r } { \text { Equation } \color{Cerulean}{( 1 ) :} } \\ { 9 x + y - 6 z = 5 } \\ { 9 ( \color{Cerulean}{1}\color{Black}{ )} + ( \color{Cerulean}{4}\color{Black}{ )} - 6 \left( \color{Cerulean}{\frac { 4 } { 3 }} \right) = 5 } \\ { 9 + 4 - 8 = 5 } \\ { 5 = 5 } \:\:\color{Cerulean}{✓}\end{array}\)	\(\begin{array} { r } { \text { Equation } \color{Cerulean}{( 2 ) :} } \\ { -6x -3y +3z = -14 } \\ { 6 ( \color{Cerulean}{1}\color{Black}{ )} - 3( \color{Cerulean}{4}\color{Black}{ )}+ 3 \left( \color{Cerulean}{\frac { 4 } { 3 }} \right) = -14 } \\ { -6-12+4 = -14 } \\ { -14= -14 } \:\:\color{Cerulean}{✓}\end{array}\)	\(\begin{array} { r } { \text { Equation } \color{Cerulean}{( 3 ) :} } \\ { 3x+2y-7z = 15 } \\ { 3 ( \color{Cerulean}{1}\color{Black}{ )} +2( \color{Cerulean}{4}\color{Black}{ )}-7 \left( \color{Cerulean}{\frac { 4 } { 3 }} \right) = 15 } \\ { 3+8-\frac{28}{3} = 15 } \\ { \frac{5}{3}= 15 } \:\:\color{red}{X}\end{array}\)