3.5: Matrices y Eliminación Gaussiana

Última actualización
Guardar como PDF

Page ID: 109844

Anonymous
LibreTexts

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Utilice la sustitución posterior para resolver sistemas lineales en forma triangular superior.
Convierta sistemas lineales en matrices aumentadas equivalentes.
Utilizar matrices y eliminación gaussiana para resolver sistemas lineales.

Sustitución de espalda

Recordemos que un sistema lineal de ecuaciones consiste en un conjunto de dos o más ecuaciones lineales con las mismas variables. Un sistema lineal que consta de tres ecuaciones en forma estándar dispuestas de manera que la variable\(x\) no aparece en ninguna ecuación después de la primera y la variable\(y\) no aparece en ninguna ecuación después de la segunda se dice que está en forma triangular superior ²². Por ejemplo,

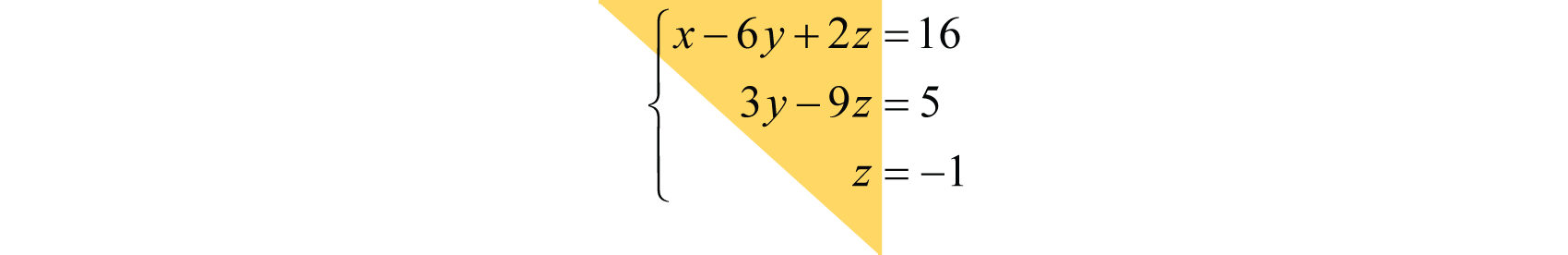
Observe que el sistema forma un triángulo donde cada ecuación sucesiva contiene una variable menos. En general,

\(\color{Cerulean}{Linear\: Systems\: in\: Upper\: Triangular\: Form}\)

\(\left\{ \begin{array} { r l } { a _ { 1 } x + b _ { 1 } y = c _ { 1 } } \\ { b _ { 2 } y = c _ { 2 } }\end{array} \right. \quad\quad\left\{ \begin{array} { r l } { a _ { 1 } x + b _ { 1 } y + c_{1}z= d _ { 1 } } \\ { b _ { 2 } y + c_{2}z = d _ { 2 }\\ \\\quad\quad\:\:\: c_{3}z = d_{3} }\end{array} \right.\)

Si un sistema lineal está en esta forma, podemos resolver fácilmente una de las variables y luego volver a sustituir para resolver las variables restantes.

Ejemplo\(\PageIndex{1}\):

Resolver:\(\left\{ \begin{aligned} 3 x - y & = 7 \\ 2 y & = - 2 \end{aligned} \right.\)

Solución

Recordemos que las soluciones a sistemas lineales con dos variables, si existen, son pares ordenados\((x, y)\). Podemos determinar el\(y\) -valor fácilmente usando la segunda ecuación.

\(\begin{aligned} 2 y & = - 2 \\ y & = - 1 \end{aligned}\)

A continuación, usa la primera ecuación\(3x − y = 7\) y el hecho de que\(y = −1\) para encontrar\(x\).

\(\begin{aligned} 3 x - y & = 7 \\ 3 x - ( \color{Cerulean}{- 1}\color{black}{ )} & = 7 \\ 3 x + 1 & = 7 \\ 3 x & = 6 \\ x & = 2 \end{aligned}\)

Respuesta:

\((2, -1)\)

Ejemplo\(\PageIndex{2}\):

Resolver:\(\left\{ \begin{aligned} x - 6 y + 2 z & = 16 \\ 3 y - 9 z & = 5 \\ z & = - 1 \end{aligned} \right.\).

Solución

Recordemos que las soluciones a sistemas lineales con tres variables, si existen, son triples ordenadas\((x, y, z)\). Usa la segunda ecuación\(3y − 9z = 5\) y el hecho de que\(z = −1\) para encontrar\(y\).

\(\begin{aligned} 3 y - 9 z & = 5 \\ 3 y - 9 (\color{Cerulean}{ - 1}\color{black}{ )} & = 5 \\ 3 y + 9 & = 5 \\ 3 y & = - 4 \\ y & = - \frac { 4 } { 3 } \end{aligned}\)

Siguiente sustituto\(y\) y\(z\) en la primera ecuación.

\(\begin{aligned} x - 6 y + 2 z & = 16 \\ x - 6 \left( \color{Cerulean}{- \frac { 4 } { 3} } \right) + 2 ( \color{Cerulean}{- 1}\color{black}{ )} & = 16 \\ x + 8 - 2 & = 16 \\ x + 6 & = 16 \\ x & = 10 \end{aligned}\)

Respuesta:

\((10, -\frac{4}{3}, -1)\)

Ejercicio\(\PageIndex{1}\)

Resolver:\(\left\{ \begin{aligned} 4 x - y + 3 z & = 1 \\ 2 y - 9 z & = - 2 \\ 3 z & = 2 \end{aligned} \right.\)

Contestar

\(\left( \frac { 1 } { 4 } , 2 , \frac { 2 } { 3 } \right)\)

www.youtube.com/V/rbuxJSQ-BVu

Matrices y Eliminación Gaussiana

En esta sección el objetivo es desarrollar una técnica que agilice el proceso de resolución de sistemas lineales. Comenzamos definiendo una matriz ²³, que es una matriz rectangular de números que consiste en filas y columnas. Dado un sistema lineal en forma estándar, creamos una matriz de coeficientes ²⁴ escribiendo los coeficientes tal y como aparecen alineados sin las variables u operaciones de la siguiente manera.

\(\quad\quad\quad\quad\quad\color{Cerulean}{Linear\:System} \quad\quad\quad\quad\quad\color{Cerulean}{Coefficient\:Matrix} \\\left\{ \begin{array} { l } { a _ { 1 } x + b _ { 1 } y + c _ { 1 } z = d _ { 1 } } \\ { a _ { 2 } x + b _ { 2 } y + c _ { 2 } z = d _ { 2 } } \\ { a _ { 3 } x + b _ { 3 } y + c _ { 3 } z = d _ { 3 } } \end{array} \right. \quad \quad\Rightarrow\quad \quad \left[ \begin{array} { l } { a _ { 1 } b _ { 1 } c _ { 1 } } \\ { a _ { 2 } b _ { 2 } c _ { 2 } } \\ { a _ { 3 } b _ { 3 } c _ { 3 } } \end{array} \right]\)

Las filas representan los coeficientes en las ecuaciones y las columnas representan los coeficientes de cada variable. Además, si incluimos una columna que representa las constantes obtenemos lo que se llama una matriz aumentada ²⁵. Para un sistema lineal con dos variables,

\(\quad\quad\quad\quad\color{Cerulean}{Linear\:System}\quad\color{Cerulean}\quad\quad{Augmented\:Matrix} \\\left\{ \begin{array} { l l } { a _ { 1 } x + b _ { 1 } y = c _ { 1 } } \\ { a _ { 2 } x + b _ { 2 } y = c _ { 2 } } \end{array} \right.\quad\quad \Leftrightarrow \quad\quad \left[ \begin{array} { l } { a _ { 1 } b _ { 1 } \left| c _ { 1 } \right. } \\ { a _ { 2 } b _ { 2 } \left| c _ { 2 } \right. } \end{array} \right]\)

Y para un sistema lineal con tres variables tenemos

\(\quad\quad\quad\quad\color{Cerulean}{Linear\:System}\quad\color{Cerulean}\quad\quad{Augmented\:Matrix} \\\left\{ \begin{array} { l } { a _ { 1 } x + b _ { 1 } y + c _ { 1 } z = d _ { 1 } } \\ { a _ { 2 } x + b _ { 2 } y + c _ { 2 } z = d _ { 2 } } \\ { a _ { 3 } x + b _ { 3 } y + c _ { 3 } z = d _ { 3 } } \end{array} \right.\quad\quad \Leftrightarrow \quad\left[ \begin{array} { l } { a _ { 1 } b _ { 1 } c _ { 1 } \left| d _ { 1 } \right. } \\ { a _ { 2 } b _ { 2 } c _ { 2 } \left| d _ { 2 } \right. } \\ { a _ { 3 } b _ { 3 } c _ { 3 } \left| d _ { 3 } \right. } \end{array} \right]\)

Nota

La línea vertical discontinua proporciona separación visual entre la matriz de coeficientes y la columna de constantes. En otros recursos de álgebra que puedas encontrar, esto a veces se omite.

Ejemplo\(\PageIndex{3}\):

Construir la matriz aumentada que corresponda a:\(\left\{ \begin{array} { l } { 9 x - 6 y = 0 } \\ { - x + 2 y = 1 } \end{array} \right.\).

Solución

Este sistema consta de dos ecuaciones lineales en forma estándar; por lo tanto, los coeficientes en la matriz aparecen como lo hacen en el sistema.

\(\left\{ \begin{array} { l } { 9 x - 6 y = 0 } \\ { - x + 2 y = 1 } \end{array} \right. \Leftrightarrow \left[ \begin{array} { c c | c } { 9 } & { - 6}&{0 } \\ { - 1 } &{ 2} &{ 1} \end{array} \right]\)

Ejemplo\(\PageIndex{4}\):

Construir la matriz aumentada que corresponde a:\(\left\{ \begin{aligned} x + 2 y - 4 z & = 5 \\ 2 x + y - 6 z & = 8 \\ 4 x - y - 12 z & = 13 \end{aligned} \right.\)

Solución

Dado que las ecuaciones se dan en forma estándar, los coeficientes aparecen en la matriz como lo hacen en el sistema.

\(\left\{ \begin{array} { c c } { x + 2 y - 4 z = 5 } \\ { 2 x + y - 6 z = 8 } \\ { 4 x - y - 12 z = 13 } \end{array} \right. \Leftrightarrow \left[ \begin{array} { c c c | c } { 1 } & { 2 } & { - 4 } & { 5 } \\ { 2 } & { 1 } & { - 6 } & { 8 } \\ { 4 } & { - 1 } & { - 12 } & { 13 } \end{array} \right]\)

Una matriz está en forma triangular superior si todos los elementos por debajo del elemento anterior distinto de cero en cada fila sucesiva son cero. Por ejemplo,

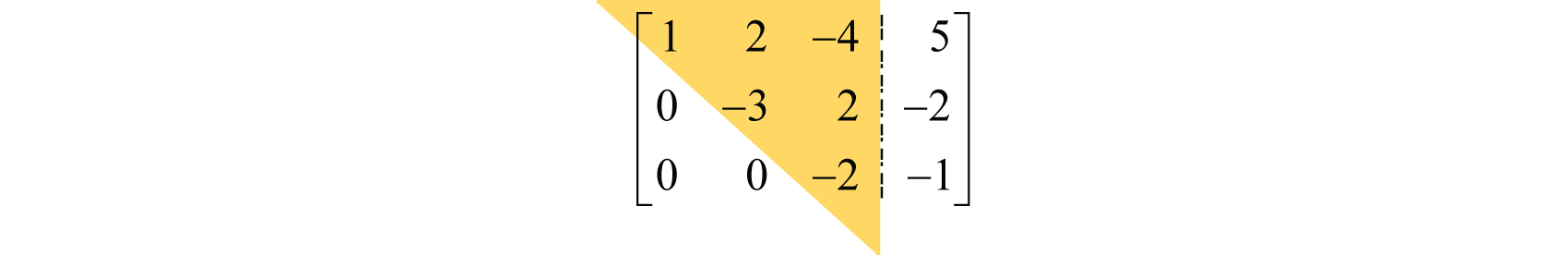
Observe que los elementos por debajo de la diagonal principal son cero y los coeficientes anteriores forman una forma triangular. En general,

\(\color{Cerulean}{Upper\:Triangular\:Form}\\\left[ \begin{array} { c c } { a _ { 1 }} & { b _ { 1 } } \\ { 0} &{ b _ { 2 } } \end{array} \right] \quad \left[ \begin{array} { c c c } { a _ { 1 }} &{ b _ { 1 }} & { c _ { 1 } } \\ { 0} &{ b _ { 2 }}&{ c _ { 2 } } \\ { 0 } & { 0} &{ c _ { 3 } } \end{array} \right]\)

Esto es importante porque en esta sección se esboza un proceso mediante el cual se pueden realizar ciertas operaciones para producir un sistema lineal equivalente en forma triangular superior para que pueda resolverse mediante el uso de retrosustitución. A continuación se describe una descripción general del proceso:

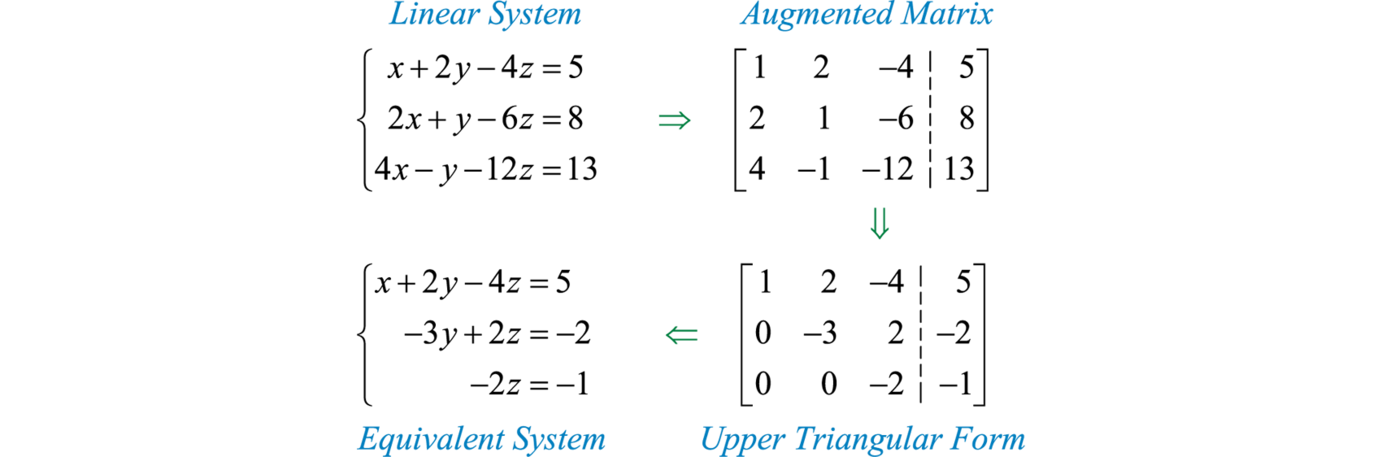
Una vez que el sistema está en forma triangular superior, podemos usar la sustitución posterior para resolverlo fácilmente. Es importante señalar que las matrices aumentadas aquí presentadas representan sistemas lineales de ecuaciones en forma estándar.

Las siguientes operaciones de fila elemental ²⁶ dan como resultado matrices aumentadas que representan sistemas lineales equivalentes:

Se pueden intercambiar dos filas cualesquiera.
Cada elemento en una fila se puede multiplicar por una constante distinta de cero.
Cualquier fila puede ser reemplazada por la suma de esa fila y un múltiplo de otra.

Nota

Estas operaciones son consistentes con las propiedades utilizadas en el método de eliminación.

Para resolver eficientemente un sistema de ecuaciones lineales, primero construya una matriz aumentada. Luego aplique las operaciones de fila elemental apropiadas para obtener una matriz aumentada en forma triangular superior. De esta forma, el sistema lineal equivalente se puede resolver fácilmente usando la sustitución posterior. Este proceso se llama eliminación gaussiana ²⁷, nombrado en honor a Carl Friedrich Gauss (1777—1855).

Figura\(\PageIndex{4}\): Carl Friedrich Gauss

Los pasos para resolver una ecuación lineal con dos variables usando la eliminación gaussiana se enumeran en el siguiente ejemplo.

Ejemplo\(\PageIndex{5}\):

Resolver usando matrices y eliminación gaussiana:\(\left\{ \begin{array} { l } { 9 x - 6 y = 0 } \\ { - x + 2 y = 1 } \end{array} \right.\).

Solución

Asegurar que las ecuaciones en el sistema estén en forma estándar antes de comenzar este proceso.

Paso 1: Construir la matriz aumentada correspondiente.

\(\left\{ \begin{array} { l } { 9 x - 6 y = 0 } \\ { - x + 2 y = 1 } \end{array} \right. \Leftrightarrow \left[ \begin{array} { c c | c} { 9} &{ - 6} & {0 } \\ { - 1} &{2}&{1 } \end{array} \right]\)

Paso 2:: Aplicar las operaciones de fila elemental para obtener la forma triangular superior. En este caso, sólo necesitamos eliminar el primer elemento de la segunda fila,\(−1\). Para ello, multiplica la segunda fila por\(9\) y agréguala a la primera fila.

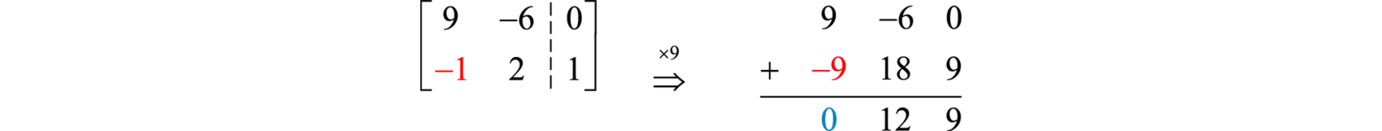
Ahora usa esto para reemplazar la segunda fila.

\(\left[ \begin{array} { c c | c } { 9 } & { - 6}&{0 } \\ {\color{Cerulean}{ 0} } & { \color{black}{12} } & { 19 } \end{array} \right]\)

Esto da como resultado una matriz aumentada en forma triangular superior.

Paso 3: Convertir de nuevo a un sistema lineal y resolver usando la sustitución de retorno. En este ejemplo, tenemos

\(\left[ \begin{array} { c c |c} { 9} &{ - 6} &{0 } \\ { \color{Cerulean}{0} } & { \color{black}{12}} &{ 9 } \end{array} \right] \Rightarrow \left\{ \begin{array} { r } { 9 x - 6 y = 0 } \\ { 12 y = 9 } \end{array} \right.\)

Resolver la segunda ecuación para\(y\),

\(\begin{array} { l } { 12 y = 9 } \\ { y = \frac { 9 } { 12 } } \\ { y = \frac { 3 } { 4 } } \end{array}\)

Sustituir este valor por\(y\) en la primera ecuación para encontrar\(x\),

\(\begin{aligned} 9 x - 6 y & = 0 \\ 9 x - 6 \left( \color{OliveGreen}{\frac { 3 } { 4 }} \right) & = 0 \\ 9 x - \frac { 9 } { 2 } & = 0 \\ 9 x & = \frac { 9 } { 2 } \\ x & = \frac { 1 } { 2 } \end{aligned}\)

Respuesta:

\(\left( \frac { 1 } { 2 } , \frac { 3 } { 4 } \right)\)

Los pasos para usar la eliminación gaussiana para resolver una ecuación lineal con tres variables se enumeran en el siguiente ejemplo.

Ejemplo\(\PageIndex{6}\):

Resolver usando matrices y eliminación gaussiana:\(\left\{ \begin{array} { c } { x + 2 y - 4 z = 5 } \\ { 2 x + y - 6 z = 8 } \\ { 4 x - y - 12 z = 13 } \end{array} \right.\)

Solución

Asegurar que las ecuaciones en el sistema estén en forma estándar antes de comenzar este proceso.

Paso 1: Construir la matriz aumentada correspondiente.

\(\left\{ \begin{array} { c c c } { x + 2 y - 4 z } & { = 5 } \\ { 2 x + y - 6 z } & { = 8 } \\ { 4 x - y - 12 z } & { = 13 } \end{array} \right.\quad \color{Cerulean}{\Rightarrow} \color{black}{\quad \left[ \begin{array} { c c c | c } { 1 } & { 2 } & { - 4 } & { 5 } \\ { 2 } & { 1 } & { - 6 } & { 8 } \\ { 4 } & { - 1 } & { - 12 } & { 13 } \end{array} \right]}\)

Paso 2: Aplicar las operaciones de fila elemental para obtener la forma triangular superior. Comenzamos eliminando el primer elemento de la segunda fila,\(2\) en este caso. Para ello multiplica la primera fila por\(−2\) y luego agréguala a la segunda fila.

\( \left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ { \color{red}{2} } & { 1 } & { - 6 } & { 8 } \\ { 4 } & { - 1 } & { - 12 } & { 13 } \end{array} \right] \stackrel{\stackrel {\times( - 2 )}{\Longrightarrow}}{}\begin{array} { c c c c }\:\;\:\:\:\: { - 2} &{ - 4} &\:\:{ 8} &{ - 10 } \\ + \:\:\:\:\:\:{ \color{red}{2}} & {\color{black}{1}} & {- 6} &{8 } \\ \hline \:\:\:\:\:\:\:\: {\color{Cerulean}{0}} &{ - 3} & {2} & { - 2 } \end{array}\)

Use esto para reemplazar la segunda fila.

\(\left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ { \color{Cerulean}{0} } & { \color{black}{- 3} } & { 2 } & { - 2 } \\ { 4 } & { - 1 } & { - 12 } & { 13 } \end{array} \right]\)

A continuación, elimina el primer elemento de la tercera fila,\(4\) en este caso, multiplicando la primera fila por\(−4\) y añadiéndola a la tercera fila.

\( \left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ { 0 } & { -3 } & { 2 } & { -2 } \\ { \color{red}{4} } & { \color{black}{- 1} } & { - 12 } & { 13 } \end{array} \right] \stackrel{\stackrel {\times( - 4 )}{\Longrightarrow}}{}\begin{array} { c c c c }\:\;\:\:\:\: { - 4} &{ - 8} &{ 16} &{ - 20 } \\ + \:\:\:\:\:\:{ \color{red}{4}} & {\color{black}{-1}} & {- 12} &{13 } \\ \hline \:\:\:\:\:\:\:\: {\color{Cerulean}{0}} &{ - 9} & {4} & { - 7 } \end{array}\)

Use esto para reemplazar la tercera fila.

\(\left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ {\color{Cerulean}{ 0} } & { \color{black}{- 3} } & { 2 } & { - 2 } \\ { \color{Cerulean}{0} } & { \color{black}{- 9} } & { 4 } & { - 7 } \end{array} \right]\)

Esto da como resultado una matriz aumentada donde los elementos debajo del primer elemento de la primera fila son cero. Siguiente eliminar el segundo elemento en la tercera fila, en este caso\(−9\). Multiplica la segunda fila por\(−3\) y agrégalo a la tercera fila.

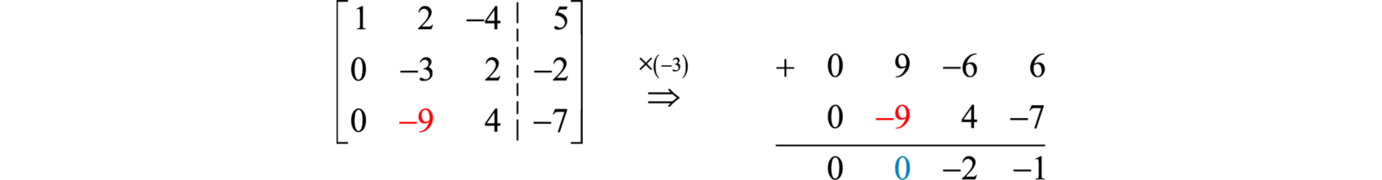
Usa esto para reemplazar la tercera fila y podemos ver que hemos obtenido una matriz en forma triangular superior.

\(\left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ { \color{Cerulean}{0} } & { \color{black}{- 3} } & { 2 } & { - 2 } \\ { \color{Cerulean}{0} } & { \color{Cerulean}{0} } & {\color{black}{ - 2} } & { - 1 } \end{array} \right]\)

Paso 3: Convertir de nuevo a un sistema lineal y resolver usando la sustitución de retorno. En este ejemplo, tenemos

\(\left[ \begin{array} { c c c |c } { 1 } & { 2 } & { - 4 } & { 5 } \\ { 0 } & { - 3 } & { 2 } & { - 2 } \\ { 0 } & { 0 } & { - 2 } & { - 1 } \end{array} \right] \Rightarrow \left\{ \begin{array} { r } { x + 2 y - 4 z = 5 } \\ { - 3 y + 2 z = - 2 } \\ { - 2 z = - 1 } \end{array} \right.\)

Respuesta:

Se deja al lector verificar que la solución es\((5, 1, \frac{1}{2})\).

Nota

Por lo general, el trabajo que implica reemplazar una fila multiplicando y agregando se realiza en el costado usando papel rascar.

Ejemplo\(\PageIndex{7}\):

Resolver usando matrices y eliminación gaussiana:\(\left\{ \begin{aligned} 2 x - 9 y + 3 z &= - 18 \\ x - 2 y - 3 z &= - 8 \\ - 4 x + 23 y + 12 z &= 47 \end{aligned} \right.\)

Solución

Comenzamos convirtiendo el sistema en una matriz de coeficientes aumentados.

\(\left\{ \begin{aligned} 2 x - 9 y + 3 z &= - 18 \\ x - 2 y - 3 z& = - 8 \\ - 4 x + 23 y + 12 z &= 47 \end{aligned} \right. \color{OliveGreen}{\Rightarrow} \color{black}{\left[ \begin{array} { c c c | c } { 2 }&{- 9 } & { 3} &{ - 18 } \\ { 1} &{ - 2 } & { - 3 } & { - 8 } \\ { - 4 } & { 23 } & { 12 } & { 47 } \end{array} \right]}\)

Las operaciones de fila elemental se simplificarán si el elemento principal distinto de cero en una fila es\(1\). Por esta razón, comience por intercambiar las filas uno y dos.

Reemplace la fila dos por la suma de\(−2\) veces la fila uno y la fila dos.

Reemplace la fila tres por la suma de\(4\) veces la fila uno y la fila tres.

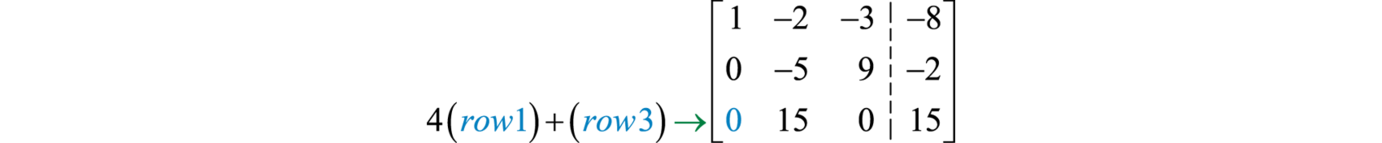
Siguiente dividir fila\(3\) por\(15\).

Intercambia la fila tres con la fila dos.

Siguiente reemplazar fila\(3\) con la suma de\(5\) veces fila dos y fila tres.

Esto da como resultado una matriz en forma triangular superior. Una matriz está en forma de escalón de fila ²⁸ si está en forma triangular superior donde está el elemento principal distinto de cero de cada fila\(1\). Podemos obtener esta forma reemplazando la fila tres con los resultados de dividirla por\(9\).

Convertir a un sistema de ecuaciones lineales y resolver por sustitución posterior.

\(\left[ \begin{array} { c c c | c} { 1} &{ - 2} &{ - 3} &{ - 8 } \\ { 0 } & { 1 } & { 0 } & { 1 } \\ { 0 } & { 0 } & { 1 } & { \frac { 1 } { 3 } } \end{array} \right] \Rightarrow \left\{ \begin{aligned} x - 2 y - 3 z & = - 8 \\ y & = 1 \\ z & = \frac { 1 } { 3 } \end{aligned} \right.\)

Aquí\(y = 1\) y\(z = \frac{1}{3}\). Sustituir en la primera ecuación para encontrar\(x\).

\(\begin{aligned} x - 2 y - 3 y & = - 8 \\ x - 2 ( \color{Cerulean}{1}\color{black}{ )} - 3 \left(\color{Cerulean}{ \frac { 1 } { 3} } \right) & = - 8 \\ x - 2 - 1 & = - 8 \\ x - 3 & = - 8 \\ x & = - 5 \end{aligned}\)

Respuesta:

Por lo tanto la solución es\(\left( - 5,1 , \frac { 1 } { 3 } \right)\).

Nota

Muchas calculadoras modernas y sistemas de álgebra computacional pueden realizar la eliminación gaussiana. Primero necesitarás averiguar cómo ingresar a una matriz. Luego usa las funciones de la calculadora para encontrar la forma de escalón de filas. Se le anima a realizar algunas investigaciones web sobre este tema para su modelo de calculadora particular.

Ejercicio\(\PageIndex{2}\)

Resolver usando eliminación gaussiana:\(\left\{ \begin{array} { c } { x - 3 y + 2 z = 16 } \\ { 4 x - 11 y - z = 69 } \\ { 2 x - 5 y - 4 z = 36 } \end{array} \right.\).

Contestar

\(( 6 , - 4 , - 1 )\)

www.youtube.com/V/8mAVVygoedm

Ejemplo\(\PageIndex{8}\):

Resolver usando matrices y eliminación gaussiana:\(\left\{ \begin{array} { c } { x - 2 y + z = 4 } \\ { 2 x - 3 y + 4 z = 7 } \\ { 4 x - 7 y + 6 z = 15 } \end{array} \right.\).

Solución

Comenzamos convirtiendo el sistema en una matriz de coeficientes aumentados.

\(\left\{ \begin{array} { c c } { x - 2 y + z = 4 } \\ { 2 x - 3 y + 4 z = 7 } \\ { 4 x - 7 y + 6 z = 15 } \end{array} \right. \color{OliveGreen}{\Rightarrow} \color{black}{ \left[ \begin{array} { c c | c } { 1} &{ - 21} &{ 4 } \\ { 2} &{ - 34}&{ 7 } \\ { 4} &{ - 76}&{ 15 } \end{array} \right]}\)

Reemplace la fila dos por\(−2\) (fila\(1\)) + (fila\(2\)) y reemplace la fila tres por\(−4\) (fila\(1\)) + (fila\(3\)).

\(\left[ \begin{array} { c c |c } { 1 } & { - 21 } & { 4 } \\ { 0 } & { 12 } & { - 1 } \\ { 0 } & { 12 } & { - 1 } \end{array} \right]\)

Reemplace la fila tres por\(−1\) (fila\(2\)) + (fila\(3\)).

\(\left[ \begin{array} { c c | c} { 1 } & { - 21 } & { 4 } \\ { 0 } & { 12 } & { - 1 } \\ { 0 } & { 00 } & { 0 } \end{array} \right]\)

La última fila indica que este es un sistema dependiente porque convertir la matriz aumentada de nuevo a ecuaciones que tenemos,

\(\left\{ \begin{aligned} x - 2 y + z & = 4 \\ y + 2 z & = - 1 \\ 0 x + 0 y + 0 z & = 0 \end{aligned} \right.\)

Obsérvese que la fila de ceros corresponde a la siguiente identidad,

\(\begin{array} { r } { 0 x + 0 y + 0 z = 0 } \\ { 0 = 0 } \end{array} \color{Cerulean}{✓}\)

En este caso, podemos expresar las infinitamente muchas soluciones en términos de\(z\). A partir de la segunda fila tenemos lo siguiente:

\(\begin{aligned} y + 2 z & = - 1 \\ y & = - 2 z - 1 \end{aligned}\)

Y a partir de la primera ecuación,

\(\begin{aligned} x - 2 y + z & = 4 \\ x - 2 ( \color{Cerulean}{- 2 z - 1}\color{black}{ )} + z & = 4 \\ x + 5 z + 2 & = 4 \\ x & = - 5 z + 2 \end{aligned}\)

Las soluciones toman la forma\((x, y, z) = (−5z + 2, −2z − 1, z)\) donde\(z\) está cualquier número real.

Respuesta:

\(( - 5 z + 2 , - 2 z - 1 , z )\)

Los sistemas dependientes e inconsistentes pueden identificarse en una matriz de coeficientes aumentados cuando los coeficientes en una fila son todos cero.

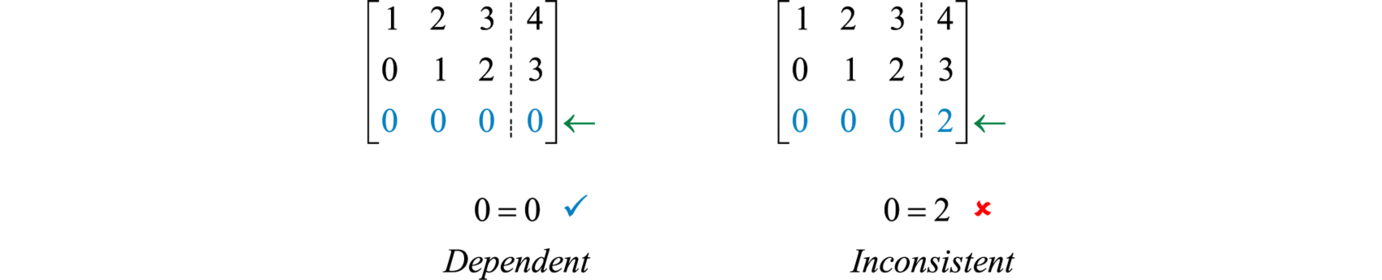
Si una fila de ceros tiene una constante correspondiente de cero entonces la matriz representa un sistema dependiente. Si la constante es distinta de cero entonces la matriz representa un sistema inconsistente.

Ejercicio\(\PageIndex{3}\)

Resolver usando matrices y eliminación gaussiana:\(\left\{ \begin{aligned} 5 x - 2 y + z & = - 3 \\ 10 x - y + 3 z & = 0 \\ - 15 x + 9 y - 2 z & = 17 \end{aligned} \right.\).

Contestar

\(\varnothing\)

www.youtube.com/v/38w0eb5e0py

Claves para llevar

Un sistema lineal en forma triangular superior se puede resolver fácilmente usando la sustitución posterior.
La matriz de coeficientes aumentados y la eliminación gaussiana se pueden utilizar para agilizar el proceso de resolución de sistemas lineales.
Para resolver un sistema usando matrices y eliminación gaussiana, primero use los coeficientes para crear una matriz aumentada. Aplicar las operaciones de fila elemental como medio para obtener una matriz en forma triangular superior. Vuelva a convertir la matriz en un sistema lineal equivalente y resolverla usando la sustitución posterior.

Ejercicio\(\PageIndex{4}\)

Resolver usando sustitución de espalda.

\(\left\{ \begin{aligned} 5 x - 3 y & = 2 \\ y & = - 1 \end{aligned} \right.\)
\(\left\{ \begin{array} { r } { 3 x + 2 y = 1 } \\ { y = 3 } \end{array} \right.\)
\(\left\{ \begin{aligned} x - 4 y & = 1 \\ 2 y & = - 3 \end{aligned} \right.\)
\(\left\{ \begin{aligned} x - 5 y & = 3 \\ 10 y & = - 6 \end{aligned} \right.\)
\(\left\{ \begin{aligned} 4 x - 3 y & = - 16 \\ 7 y & = 0 \end{aligned} \right.\)
\(\left\{ \begin{aligned} 3 x - 5 y & = - 10 \\ 4 y & = 8 \end{aligned} \right.\)
\(\left\{ \begin{aligned} 2 x + 3 y & = - 1 \\ 3 y & = 2 \end{aligned} \right.\)
\(\left\{ \begin{aligned} 6 x - y & = - 3 \\ 4 y & = 3 \end{aligned} \right.\)
\(\left\{ \begin{aligned} x - y & = 0 \\ 2 y & = 0 \end{aligned} \right.\)
\(\left\{ \begin{aligned} 2 x + y & = 2 \\ 3 y & = 0 \end{aligned} \right.\)
\(\left\{ \begin{aligned} x + 3 y - 4 z & = 1 \\ y - 3 z & = - 2 \\ z & = 3 \end{aligned} \right.\)
\(\left\{ \begin{aligned} x - 5 y + 4 z & = - 1 \\ y - 7 z & = 10 \\ z & = - 2 \end{aligned} \right.\)
\(\left\{ \begin{aligned} x - 6 y + 8 z & = 2 \\ 3 y - 4 z & = - 4 \\ 2 z & = - 1 \end{aligned} \right.\)
\(\left\{ \begin{aligned} 2 x - y + 3 z & = - 9 \\ 2 y + 6 z & = - 2 \\ 3 z & = 2 \end{aligned} \right.\)
\(\left\{ \begin{aligned} 10 x - 3 y + z & = 13 \\ 11 y - 3 z & = 9 \\ 2 z & = - 6 \end{aligned} \right.\)
\(\left\{ \begin{aligned} 3 x - 2 y + 5 z & = - 24 \\ 4 y + 5 z & = 3 \\ 4 z & = - 12 \end{aligned} \right.\)
\(\left\{ \begin{aligned} x - y + 2 z & = 1 \\ 2 y + z & = 1 \\ 3 z & = - 1 \end{aligned} \right.\)
\(\left\{ \begin{aligned} x + 2 y - z & = 2 \\ y - 3 z & = 1 \\ 6 z & = 1 \end{aligned} \right.\)
\(\left\{ \begin{aligned} x - 9 y + 5 z & = - 3 \\ 2 y & = 10 \\ 3 z & = 27 \end{aligned} \right.\)
\(\left\{ \begin{aligned} 4 x - z & = 3 \\ 3 y - 2 z & = - 1 \\ 2 z & = - 8 \end{aligned} \right.\)

Contestar

1. \(\left( - \frac { 1 } { 5 } , - 1 \right)\)

3. \(\left( - 5 , - \frac { 3 } { 2 } \right)\)

5. \((-4, 0)\)

7. \(\left( - \frac { 3 } { 2 } , \frac { 2 } { 3 } \right)\)

9. \((0,0)\)

11. \((-8, 7, 3)\)

13. \(\left( - 6 , - 2 , - \frac { 1 } { 2 } \right)\)

15. \(\left( \frac { 8 } { 5 } , 0 , - 3 \right)\)

17. \(\left( \frac { 7 } { 3 } , \frac { 2 } { 3 } , - \frac { 1 } { 3 } \right)\)

19. \((-3, 5, 9)\)

Ejercicio\(\PageIndex{5}\)

Construir la matriz aumentada correspondiente (no resolver).

\(\left\{ \begin{array} { c } { x + 2 y = 3 } \\ { 4 x + 5 y = 6 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 6 x + 5 y = 4 } \\ { 3 x + 2 y = 1 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x - 2 y = 1 } \\ { 2 x - y = 1 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { x - y = 2 } \\ { - x + y = - 1 } \end{array} \right.\)
\(\left\{ \begin{aligned} - x + 8 y & = 3 \\ 2 y & = 2 \end{aligned} \right.\)
\(\left\{ \begin{array} { r } { 3 x - 2 y = 4 } \\ { - y = 5 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 3 x - 2 y + 7 z = 8 } \\ { 4 x - 5 y - 10 z = 6 } \\ { - x - 3 y + 2 z = - 1 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { x - y - z = 0 } \\ { 2 x - y + 3 z = - 1 } \\ { - x + 4 y - 3 z = - 2 } \end{array} \right.\)
\(\left\{ \begin{aligned} x - 9 y + 5 z & = - 3 \\ 2 y & = 10 \\ 3 z & = 27 \end{aligned} \right.\)
\(\left\{ \begin{array} { c } { 4 x - z = 3 } \\ { 3 y - 2 z = - 1 } \\ { 2 z = - 8 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { 8 x + 2 y = - 13 } \\ { - 2 y + z = 1 } \\ { 12 x - 5 z = - 18 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x - 3 z = 2 } \\ { y + 6 z = 4 } \\ { 2 x + 3 y = 12 } \end{array} \right.\)

Contestar

1. \(\left[ \begin{array} { c c | c } { 1} & {2} &{ 3 } \\ { 4}&{5} &{ 6 } \end{array} \right]\)

3. \(\left[ \begin{array} { c c | c} { 1} &{ - 2} &{ 1 } \\ { 2} &{ - 1} &{ 1 } \end{array} \right]\)

5. \(\left[ \begin{array} { c c | c } { - 1} &{8} &{ 3 } \\ { 0} & {2} &{ 2 } \end{array} \right]\)

7. \(\left[ \begin{array} { c c c | c} { 3 } & { - 2 } & { 7 } & { 8 } \\ { 4} &{ - 5 } & { - 10 } & { 6 } \\ { - 1 } & { - 3 } & { 2 } & { - 1 } \end{array} \right]\)

9. \(\left[ \begin{array} { c c c | c } { 1 } & { - 9} &{5} &{ - 3 } \\ { 0 } & { 2} &{0 } & { 10 } \\ { 0 } & { 0} &{3 } & { 27 } \end{array} \right]\)

11. \(\left[ \begin{array} { c c c | c } { 8 } & { 2 } & { 0 } &{ - 13 } \\ { 0 } & { - 2 } & { 1 } & { 1 } \\ { 12 } & { 0 } & { - 5 } & { - 18 } \end{array} \right]\)

Ejercicio\(\PageIndex{6}\)

Resolver usando matrices y eliminación gaussiana.

\(\left\{ \begin{array} { l } { x - 5 y = 2 } \\ { 2 x - y = 1 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { x - 2 y = - 1 } \\ { x + y = 1 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 10 x - 7 y = 15 } \\ { - 2 x + 3 y = - 3 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { 9 x - 10 y = 2 } \\ { 3 x + 5 y = - 1 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 3 x + 5 y = 8 } \\ { 2 x - 3 y = 18 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 5 x - 3 y = - 14 } \\ { 7 x + 2 y = - 1 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { 9 x + 15 y = 5 } \\ { 3 x + 5 y = 7 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { 6 x - 8 y = 1 } \\ { - 3 x + 4 y = - 1 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x + y = 0 } \\ { x - y = 0 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 7 x - 3 y = 0 } \\ { 3 x - 7 y = 0 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { 2 x - 3 y = 4 } \\ { - 10 x + 15 y = - 20 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 6 x - 10 y = 20 } \\ { - 3 x + 5 y = - 10 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x + y - 2 z = - 1 } \\ { - x + 2 y - z = 1 } \\ { x - y + z = 2 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { x - y + z = - 2 } \\ { x + 2 y - z = 6 } \\ { - x + y - 2 z = 3 } \end{array} \right.\)
\(\left\{ \begin{aligned} 2 x - y + z & = 2 \\ x - y + z & = 2 \\ - 2 x + 2 y - z & = - 1 \end{aligned} \right.\)
\(\left\{ \begin{array} { l } { 3 x - y + 2 z = 7 } \\ { - x + 2 y + z = 6 } \\ { x + 3 y - 2 z = 1 } \end{array} \right.\)
\(\left\{ \begin{aligned} x - 3 y + z & = 6 \\ - x - y + 2 z & = 4 \\ 2 x + y + z & = 3 \end{aligned} \right.\)
\(\left\{ \begin{aligned} 4 x - y + 2 z & = 12 \\ x - 3 y + 2 z & = 7 \\ - 2 x + 3 y + 4 z & = - 16 \end{aligned} \right.\)
\(\left\{ \begin{array} { c } { 2 x - 4 y + 6 z = - 4 } \\ { 3 x - 2 y + 5 z = - 2 } \\ { 5 x - y + 2 z = 1 } \end{array} \right.\)
\(\left\{ \begin{aligned} 3 x + 6 y + 9 z & = 6 \\ 2 x - 2 y + 3 z & = 0 \\ - 3 x + 18 y - 12 z & = 5 \end{aligned} \right.\)
\(\left\{ \begin{array} { l } { - x + y - z = - 2 } \\ { 3 x - 2 y + 5 z = 1 } \\ { 3 x - 5 y - z = 3 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { x + 2 y + 3 z = 4 } \\ { 3 x + 8 y + 13 z = 21 } \\ { 2 x + 5 y + 8 z = 16 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { 2 x - 4 y - 5 z = 3 } \\ { - x + y + z = 1 } \\ { 3 x - 4 y - 5 z = - 4 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 5 x - 3 y - 2 z = 4 } \\ { 3 x - 6 y + 4 z = - 6 } \\ { - x + 2 y - z = 2 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { - 2 x - 3 y + 12 z = 4 } \\ { 4 x - 5 y - 10 z = - 1 } \\ { - x - 3 y + 2 z = 0 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { 3 x - 2 y + 5 z = 10 } \\ { 4 x + 3 y - 3 z = - 6 } \\ { x + y + z = 2 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { x + 2 y + z = - 3 } \\ { x + 6 y + 3 z = 7 } \\ { x + 4 y + 2 z = 2 } \end{array} \right.\)
\(\left\{ \begin{array} { c } { 2 x - y + z = 1 } \\ { 4 x - y + 3 z = 5 } \\ { 2 x + y + 3 z = 7 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 2 x + 3 y - 4 z = 0 } \\ { 3 x - 5 y + 3 z = - 10 } \\ { 5 x - 2 y + 5 z = - 4 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 3 x - 2 y + 9 z = 2 } \\ { - 2 x - 5 y - 4 z = 3 } \\ { 5 x - 3 y + 3 z = 15 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 8 x + 2 y = - 13 } \\ { - 2 y + z = 1 } \\ { 12 x - 5 z = - 18 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { x - 3 z = 2 } \\ { y + 6 z = 4 } \\ { 2 x + 3 y = 12 } \end{array} \right.\)
\(\left\{ \begin{aligned} 9 x + 3 y - 11 z & = 6 \\ 2 x + y - 3 z & = 1 \\ 7 x + 2 y - 8 z & = 3 \end{aligned} \right.\)
\(\left\{ \begin{array} { c } { 3 x - y - z = 4 } \\ { - 5 x + y + 2 z = - 3 } \\ { 6 x - 2 y - 2 z = 8 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 2 x - 4 y + 3 z = 15 } \\ { 3 x - 5 y + 2 z = 18 } \\ { 5 x + 2 y - 6 z = 0 } \end{array} \right.\)
\(\left\{ \begin{array} { l } { 3 x - 4 y - 3 z = - 14 } \\ { 4 x + 2 y + 5 z = 12 } \\ { - 5 x + 8 y - 4 z = - 3 } \end{array} \right.\)

Contestar

1. \(\left( \frac { 1 } { 3 } , - \frac { 1 } { 3 } \right)\)

3. \(\left( \frac { 3 } { 2 } , 0 \right)\)

5. \(( 6 , - 2 )\)

7. \(\varnothing\)

9. \((0,0)\)

11. \(\left( x , \frac { 2 } { 3 } x - \frac { 4 } { 3 } \right)\)

13. \((2, 3, 3)\)

15. \((0, 1, 3)\)

17. \((1, -1, 2)\)

19. \((\left( \frac { 1 } { 2 } , \frac { 1 } { 2 } , - \frac { 1 } { 2 } \right)\)

21. \(\varnothing\)

23. \((-7, -13, 7)\)

25. \((1, 0, \frac{1}{2})\)

27. \(\left( - 8 , - \frac { 1 } { 2 } z + \frac { 5 } { 2 } , z \right)\)

29. \((-1, 2, 1)\)

31. \(\left( - \frac { 3 } { 2 } , - \frac { 1 } { 2 } , 0 \right)\)

33. \(\varnothing\)

35. \((2, -2, 1)\)

Ejercicio\(\PageIndex{7}\)

Investigar y discutir la historia de la eliminación gaussiana. ¿A quién se le atribuye el primer desarrollo de este proceso? Publica algo que te pareció interesante relacionado con esta historia.
Investigar y discutir la historia de la notación matricial moderna. ¿A quién se le atribuye el desarrollo? ¿En qué campos se utilizan hoy en día? Publique sus hallazgos en el panel de discusión.

Contestar: 1. La respuesta puede variar

Notas al pie

²² Un sistema lineal que consiste en ecuaciones con tres variables en forma estándar dispuestas de manera que la variable\(x\) no aparezca después de la primera ecuación y la variable\(y\) no aparezca después de la segunda ecuación.

²³ Una matriz rectangular de números que consta de filas y columnas.

²⁴ La matriz de coeficientes de un sistema lineal en forma estándar escrita a medida que aparecen alineados sin las variables u operaciones.

²⁵ La matriz de coeficientes con la columna de constantes incluida.

²⁶ Operaciones que se pueden realizar para obtener sistemas lineales equivalentes.

²⁷ Pasos utilizados para obtener un sistema lineal equivalente en forma triangular superior para que pueda resolverse mediante sustitución posterior.

²⁸ Una matriz en forma triangular donde el elemento principal distinto de cero de cada fila es 1