4.1: Álgebra de Funciones
- Page ID
- 109805
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Habilidades para desarrollar
- Identificar y evaluar funciones polinómicas.
- Sumar y restar funciones.
- Multiplicar y dividir funciones.
- Agrega funciones gráficamente.
Funciones polinómicas
Cualquier polinomio con una variable es una función y se puede escribir en la forma
\(f(x)=a_nx^n+a_{n−1}x^{n−1} + ⋯ +a_1x + a_0.\)
Aquí\(a_{n}\) representa cualquier número real y\(n\) representa cualquier número entero. El grado de un polinomio con una variable es el mayor exponente de todos los términos. Normalmente, organizamos términos de polinomios en orden descendente en función de su grado y los clasificamos de la siguiente manera:
\(\begin{array} { l r } { f ( x ) = 2 } & { \color{Cerulean} { Constant\: function\: (degree }\: 0 ) } \\ { g ( x ) = 3 x + 2 } & { \color{Cerulean} { Linear\: function\: (degree\: } 1 ) } \\ { h ( x ) = 4 x ^ { 2 } + 3 x + 2 } & { \color{Cerulean} { Quadratic\: function\: (degree\: } 2 ) } \\ { r ( x ) = 5 x ^ { 3 } + 4 x ^ { 2 } + 3 x + 2}&{ \color{Cerulean} { Cubic\: function\: (degree\: } 3 ) } \end{array}\)
En este libro de texto, llamamos a cualquier polinomio con grado superior a\(3\) un\(n\) polinomio de grado th. Por ejemplo, si el grado es\(4\), lo llamamos polinomio de cuarto grado; si el grado lo es\(5\), lo llamamos polinomio de quinto grado, y así sucesivamente.
Ejemplo\(\PageIndex{1}\):
Dado\(f(x)=x^{2}−8x+17\), encontrar\(f(2)\) y\(f(4)\).
Solución
Reemplazar cada instancia de\(x\) por el valor dado dentro de los paréntesis.
| \(\begin{aligned} f ( \color{Cerulean}{2}\color{black}{ )} & = ( \color{Cerulean}{2}\color{black}{ )} ^ { 2 } - 8 ( \color{Cerulean}{2}\color{black}{ )} + 17 \\ & = 4 - 16 + 17 \\ & = 4 + 1 \\ & = 5 \end{aligned}\) | \(\begin{aligned} f ( \color{Cerulean}{4}\color{black}{ ) }& = ( \color{Cerulean}{4}\color{black}{ )} ^ { 2 } - 8 ( \color{Cerulean}{4}\color{black}{ )} + 17 \\ & = 16 - 32 + 17 \\ & = - 16 + 17 \\ & = 1 \end{aligned}\) |
Podemos escribir\(f(2)=5\) y\(f(4)=1\). Recuerda eso\(f(x)=y\) y así podemos interpretar estos resultados en la gráfica de la siguiente manera:
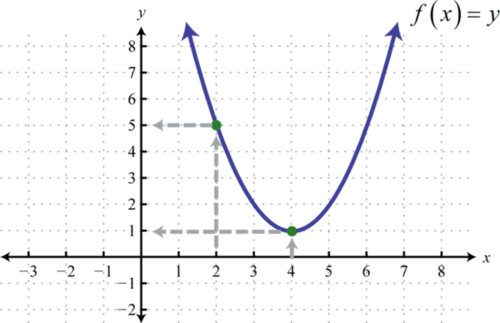
Mesa\(\PageIndex{1}\)
Respuesta:
\( f(2)=5; f(4)=1\)
A menudo se nos pedirá evaluar polinomios para expresiones algebraicas.
Ejemplo\(\PageIndex{2}\):
Dado\(g(x)=x^{3}−x+5\), encontrar\(g(−2u)\) y\(g(x−2)\).
Solución
Reemplazar\(x\) con las expresiones dadas dentro de los paréntesis.
| \(\begin{aligned} g (\color{Cerulean}{ - 2 u} \color{black}{) }& = (\color{Cerulean}{ - 2 u}\color{black}{ )} ^ { 3 } - ( \color{Cerulean}{- 2 u}\color{black}{ )} + 5 \\ & = - 8 u ^ { 3 } + 2 u + 5 \end{aligned}\) | \(\begin{aligned} g ( \color{Cerulean}{x - 2}\color{black}{ )} & = ( \color{Cerulean}{x - 2}\color{black}{ )} ^ { 3 } - (\color{Cerulean}{ x - 2}\color{black}{)} +5 \\ & = ( x - 2 ) (x-2)(x-2) - ( x -2) + 5 \\ & = ( x - 2 ) ( x^{2} - 4x +4 ) -x +7 \\ & = x ^ { 3 } - 4 x ^ { 2 } + 4 x - 2x^{2} + 8x -8 -x +7 \\ & = x ^ { 3 } - 6 x ^ { 2 } + 11x - 1 \end{aligned}\) |
Respuesta:
\(g(−2u)=−8u^{2}+2u+5\)y\(g(x−2)=x^{3}−6x^{2}+11x−1\)
La altura de un objeto lanzado hacia arriba, ignorando los efectos de la resistencia al aire, se puede modelar con la siguiente función cuadrática:
\(h(t)=−\frac{1}{2}gt^2+v_{0}t+s_{0}\)
Con esta fórmula, la altura se\(h(t)\) puede calcular en cualquier momento dado\(t\) después de lanzar el objeto. La letra\(g\) representa la aceleración debida a la gravedad en la superficie de la Tierra, que es\(32\) pies por segundo al cuadrado (o, usando unidades métricas,\(g = 9.8\) metros por segundo al cuadrado). La variable\(v_{0}\), pronunciada “v-nada”, o a veces “v-cero”, representa la velocidad inicial del objeto, y\(s_{0}\) representa la altura inicial desde la que se lanzó el objeto.
Ejemplo\(\PageIndex{3}\)
Un objeto es lanzado desde el suelo a una velocidad de\(64\) pies por segundo. Escribe una función que modele la altura del objeto y utilízala para calcular la altura de los objetos en\(1\) segundo y en\(3.5\) segundos.
Solución
Sabemos que la aceleración debida a la gravedad es\(g = 32\) pies por segundo cuadrado y se nos da la velocidad inicial\(v_{0}=64\) pies por segundo. Dado que el objeto es lanzado desde el suelo, la altura inicial es\(s_{0}=0\) pies. Cree el modelo matemático sustituyendo estos coeficientes en la siguiente fórmula:
\(\begin{array} { l } { h ( t ) = - \frac { 1 } { 2 } g t ^ { 2 } + v _ { 0 } t + s _ { 0 } } \\ { h ( t ) = - \frac { 1 } { 2 } ( \color{Cerulean}{32}\color{black}{ )} t ^ { 2 } + ( \color{Cerulean}{64}\color{black}{ )} t + \color{Cerulean}{0} } \\ { h ( t ) = - 16 t ^ { 2 } + 64 t } \end{array}\)
Utilice este modelo para calcular la altura del objeto en\(1\) segundos y\(3.5\) segundos.
\(\begin{array} { l } { h ( \color{Cerulean}{1}\color{black}{ )} = - 16 ( \color{Cerulean}{1}\color{black}{ )} ^ { 2 } + 64 ( \color{Cerulean}{1}\color{black}{ )} = - 16 + 64 = 48 } \\ { h ( \color{Cerulean}{3.5}\color{black}{ )} = - 16 ( \color{Cerulean}{3.5}\color{black}{ )} ^ { 2 } + 64 ( \color{Cerulean}{3.5}\color{black}{ )} = - 196 + 224 = 28 } \end{array}\)
Respuesta:
\(h ( t ) = - 16 t ^ { 2 } + 64 t\); Al\(1\) segundo el objeto se encuentra a una altura de\(48\) pies, y a los\(3.5\) segundos está a una altura de\(28\) pies.
Ejercicio\(\PageIndex{1}\)
Un objeto se deja caer desde una altura de 6 metros. Escribe una función que modele la altura del objeto y utilízala para calcular la altura del objeto en\(1\) segundo lugar después de que se caiga.
- Contestar
-
\(h ( t ) = - 4.9 t ^ { 2 } + 6\); Al\(1\) segundo el objeto se encuentra a una altura de\(1.1\) metros.
www.youtube.com/V/YY8KZQSPZXi
Sumando y restando funciones
La notación utilizada para indicar suma 1 y resta 2 de funciones sigue:
Adición de funciones:\((f+g)(x)=f(x)+g(x)\)
Resta de funciones:\((f−g)(x)=f(x)−g(x)\)
Al usar la notación de funciones, tenga cuidado de agrupar toda la función y sumar o restar en consecuencia.
Ejemplo\(\PageIndex{4}\)
Dado\(f(x)=x^{3}−5x−7\) y\(g(x)=3x^{2}+7x−2\), encontrar\((f+g)(x)\) y\((f−g)(x)\).
Solución
La notación\(f+g\) indica que debemos agregar las expresiones dadas.
\(\begin{aligned} ( f + g ) ( x ) & = f ( x ) + g ( x ) \\ & = \left( x ^ { 3 } - 5 x - 7 \right) + \left( 3 x ^ { 2 } + 7 x - 2 \right) \\ & = x ^ { 3 } - 5 x - 7 + 3 x ^ { 2 } + 7 x - 2 \\ & = x ^ { 3 } + 3 x ^ { 2 } + 2 x - 9 \end{aligned}\)
La notación\(f−g\) indica que debemos restar las expresiones dadas. Al restar, los paréntesis se vuelven muy importantes. Recordemos que podemos eliminarlos después de aplicar la propiedad distributiva.
\(\begin{aligned} ( f - g ) ( x ) & = f ( x ) - g ( x ) \\ & = \left( x ^ { 3 } - 5 x - 7 \right) - \left( 3 x ^ { 2 } + 7 x - 2 \right) \\ & = x ^ { 3 } - 5 x - 7 - 3 x ^ { 2 } - 7 x + 2 \\ & = x ^ { 3 } - 3 x ^ { 2 } - 12 x - 5 \end{aligned}\)
Respuesta:
\((f+g)(x)=x^{3}+3x^{2}+2x−9\)y\((f−g)(x)=x^{3}−3x^{2}−12x−5\)
Se nos puede pedir que evaluemos la suma o diferencia de dos funciones. Tenemos la opción de encontrar primero la suma o diferencia en general y luego usar la función resultante para evaluar para la variable dada, o evaluar cada una primero y luego encontrar la suma o diferencia.
Ejemplo\(\PageIndex{5}\)
Evaluar\((f−g)(3)\) dado\(f(x)=5x^{2}−x+4\) y\(g(x)=x^{2}+2x−3\).
Solución
Primero, encuentra\((f−g)(x)\).
\(\begin{aligned} ( f - g ) ( x ) & = f ( x ) - g ( x ) \\ & = \left( 5 x ^ { 2 } - x + 4 \right) - \left( x ^ { 2 } + 2 x - 3 \right) \\ & = 5 x ^ { 2 } - x + 4 - x ^ { 2 } - 2 x + 3 \\ & = 4 x ^ { 2 } - 3 x + 7 \end{aligned}\)
Por lo tanto,
\(( f - g ) ( x ) = 4 x ^ { 2 } - 3 x + 7\).
A continuación, sustituya\(3\) la variable\(x\).
\(\begin{aligned} ( f - g ) ( \color{OliveGreen}{3}\color{black}{ )} & = 4 ( \color{OliveGreen}{3}\color{black}{ )} ^ { 2 } - 3 (\color{OliveGreen}{ 3}\color{black}{ )} + 7 \\ & = 36 - 9 + 7 \\ & = 34 \end{aligned}\)
De ahí\((f−g)(3)=34\).
Solución alternativa
Ya que\((f−g)(3)=f(3)−g(3)\), podemos encontrar\(f(3)\)\(g(3)\) y luego restar los resultados.
| \(\begin{aligned} f ( x ) & = 5 x ^ { 2 } - x + 4 \\ f ( \color{Cerulean}{3}\color{black}{ )} & = 5 ( \color{Cerulean}{3}\color{black}{ )} ^ { 2 } - ( \color{Cerulean}{3}\color{black}{ )} + 4 \\ & = 45 - 3 + 4 \\ & = 46 \end{aligned}\) | \(\begin{aligned} g ( x ) & = x ^ { 2 } + 2 x - 3 \\ g ( \color{Cerulean}{3}\color{black}{ )} & = (\color{Cerulean}{ 3}\color{black}{ )} ^ { 2 } + 2 ( \color{Cerulean}{3}\color{black}{ )} - 3 \\ & = 9 + 6 - 3 \\ & = 12 \end{aligned}\) |
Por lo tanto,
\(\begin{aligned} ( f - g ) ( 3 ) & = f ( 3 ) - g ( 3 ) \\ & = 46 - 12 \\ & = 34 \end{aligned}\)
Observe que obtenemos la misma respuesta.
Respuesta:
\((f−g)(3)=34\)
Nota
Si se van a evaluar múltiples valores, lo mejor es encontrar primero la suma o diferencia en general y luego utilizarla para evaluar.
Ejercicio\(\PageIndex{2}\)
Evaluar\((f+g)(−1)\) dado\(f(x)=x^{3}+x−8\) y\(g(x)=2x^{2}−x+9\).
- Contestar
-
\(2\)
www.youtube.com/v/aykzz9u6xPW
Multiplicar y dividir funciones
La notación utilizada para indicar multiplicación 3 y división 4 de funciones sigue:
| Multiplicación de funciones: | \(( f \cdot g ) ( x ) = f ( x ) \cdot g ( x )\) |
|---|---|
| División de funciones: | \(( f / g ) ( x ) = \frac { f ( x ) } { g ( x ) } , \text { where } g ( x ) \neq 0\) |
Ejemplo\(\PageIndex{6}\):
Dado\(f(x)=15x^{4}−9x^{3}+6x^{2}\) y\(g(x)=3x^{2}\), encontrar\((f⋅g)(x)\) y\((f/g)(x)\).
Solución
La notación\(f⋅g\) indica que debemos multiplicar. Aplicar la propiedad distributiva y simplificar.
\(\begin{aligned} ( f \cdot g ) ( x ) & = f ( x ) \cdot g ( x ) \\ & = \left( 15 x ^ { 4 } - 9 x ^ { 3 } + 6 x ^ { 2 } \right) \left( 3 x ^ { 2 } \right) \\ & = 15 x ^ { 4 } \cdot \color{Cerulean}{3 x ^ { 2 }}\color{black}{ -} 9 x ^ { 3 } \cdot \color{Cerulean}{3 x ^ { 2} }\color{black}{ +} 6 x ^ { 2 } \cdot \color{Cerulean}{3 x ^ { 2} } \\ & = 45 x ^ { 6 } - 27 x ^ { 5 } + 18 x ^ { 4 } \end{aligned}\)
La notación\(f /g\) indica que debemos dividir. Para este cociente, asuma\(x ≠ 0\).
\(\begin{aligned} ( f / g ) ( x ) & = \frac { f ( x ) } { g ( x ) } \\ & = \frac { 15 x ^ { 4 } - 9 x ^ { 3 } + 6 x ^ { 2 } } { 3 x ^ { 2 } } \\ & = \frac { 15 x ^ { 4 } } { 3 x ^ { 2 } } - \frac { 9 x ^ { 3 } } { 3 x ^ { 2 } } + \frac { 6 x ^ { 2 } } { 3 x ^ { 2 } } \\ & = 5 x ^ { 2 } - 3 x + 2 \end{aligned}\)
Respuesta:
\((f⋅g)(x)=45x^{6}−27x^{5}+18x^{4}\)y\((f/g)(x)=5x^{2}−3x+2\) dónde\(x≠0\).
Ejemplo\(\PageIndex{7}\):
Dado\(f(x)=6x−5\) y\(g(x)=3x^{2}−2x−1\), evaluar\((f⋅g)(0)\) y\((f⋅g)(−1)\)
Solución
Comience por encontrar\((f⋅g)(x)\).
\(\begin{aligned} ( f \cdot g ) ( x ) & = f ( x ) \cdot g ( x ) \\ & = ( 6 x - 5 ) \left( 3 x ^ { 2 } - 2 x - 1 \right) \\ & = 18 x ^ { 3 } - 12 x ^ { 2 } - 6 x - 15 x ^ { 2 } + 10 x + 5 \\ & = 18 x ^ { 3 } - 27 x ^ { 2 } + 4 x + 5 \end{aligned}\)
Por lo tanto\(( f \cdot g ) ( x ) = 18 x ^ { 3 } - 27 x ^ { 2 } + 4 x + 5\), y tenemos,
| \(\begin{aligned} ( f \cdot g ) ( \color{Cerulean}{0}\color{black}{ )} & = 18 ( \color{Cerulean}{0}\color{black}{ )} ^ { 3 } - 27 ( \color{Cerulean}{0}\color{black}{ )} ^ { 2 } + 4 ( \color{Cerulean}{0}\color{black}{ )} + 5 \\ & = 5 \end{aligned}\) | \(\begin{aligned} ( f \cdot g ) ( \color{Cerulean}{-1}\color{black}{ )} & = 18 ( \color{Cerulean}{-1}\color{black}{ )} ^ { 3 } - 27 ( \color{Cerulean}{-1}\color{black}{ )} ^ { 2 } + 4 ( \color{Cerulean}{-1}\color{black}{ )} + 5 \\ & = -18-27-4+5\\ &=-44 \end{aligned}\) |
Respuesta:
\(( f \cdot g ) ( 0 ) = 5 \text { and } ( f \cdot g ) ( - 1 ) = - 44\)
Ejercicio\(\PageIndex{3}\)
Evaluar\((f⋅g)(−1)\) dado\(f(x)=x^{3}+x−8\) y\(g(x)=2x^{2}−x+9\).
- Contestar
-
\(-120\)
www.youtube.com/v/vyzfgca9cxg
Adición de funciones gráficamente
Aquí exploramos la geometría de agregar funciones. Una forma de hacerlo es usar el hecho de que\((f+g)(x)=f(x)+g(x)\). Sumar las funciones juntas usando x -valores para los cuales se definen tanto f como g.
Ejemplo\(\PageIndex{8}\)
Utilice las gráficas de\(f\) y\(g\) para graficar\(f+g\). También, dar el dominio de\(f+g\).
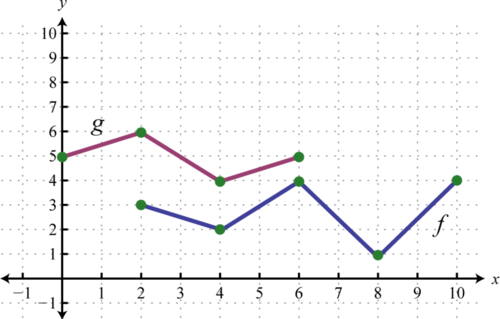
Solución
En este caso, ambas funciones se definen para\(x\) -valores entre\(2\) y\(6\). Utilizaremos\(2\),\(4\), y\(6\) como valores representativos en el dominio de\(f+g\) para bosquejar su gráfica.
\(\begin{array} { l } { ( f + g ) ( \color{Cerulean}{2}\color{black}{ )} = f ( \color{Cerulean}{2}\color{black}{ )} + g (\color{Cerulean}{ 2}\color{black}{ )} = 3 + 6 = 9 } \\ { ( f + g ) ( \color{Cerulean}{4}\color{black}{ )} = f ( \color{Cerulean}{4}\color{black}{ )} + g ( \color{Cerulean}{4}\color{black}{ )} = 2 + 4 = 6 } \\ { ( f + g ) ( \color{Cerulean}{6}\color{black}{ )} = f ( \color{Cerulean}{6}\color{black}{ )} + g ( \color{Cerulean}{6}\color{black}{ )} = 4 + 5 = 9 } \end{array}\)
Esboce la gráfica de f+g usando las tres soluciones de pares ordenadas\((2,9), (4,6)\), y\((6,9)\).
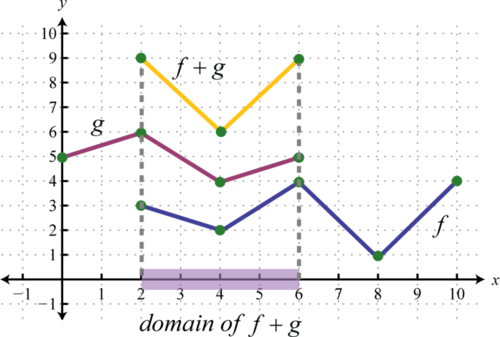
Respuesta:
\(f+g\)graficado arriba tiene dominio\([2,6]\).
Ejemplo\(\PageIndex{9}\)
Utilice las gráficas de\(f\) y\(g\) para graficar\(f+g\). También, dar el dominio de\(f+g\).
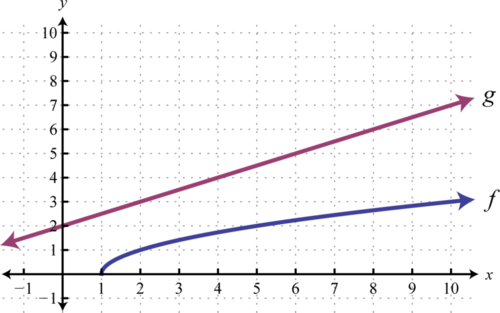
Solución
Otra forma de agregar funciones no negativas gráficamente es copiar el segmento de línea formado desde el\(x\) eje -a una de las funciones sobre la otra como se ilustra a continuación.
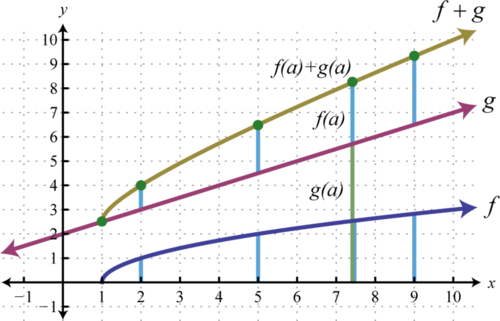
El segmento de línea desde el\(x\) eje -hasta la función\(f\) representa\(f(a)\). Copia este segmento de línea en la otra función sobre el mismo punto; el punto final representa\(f(a)+g(a)\). Hacer esto por varios puntos nos permite obtener un boceto rápido de la gráfica combinada. En este ejemplo, el dominio de\(f+g\) se limita a los\(x\) -valores para los que\(f\) se define.
Respuesta:
Dominio:\([1,∞)\)
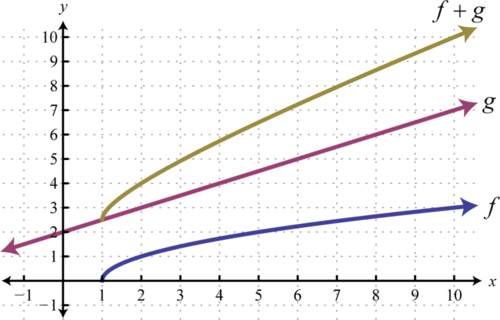
En general, el dominio de\(f+g\) es la intersección del dominio de\(f\) con el dominio de\(g\). De hecho, este es el caso de todas las operaciones aritméticas con una consideración extra para la división. Al dividir funciones, nos preocupamos por eliminar cualquier valor que haga que el denominador sea cero. Esto se discutirá con más detalle a medida que avancemos en álgebra.
Claves para llevar
- Cualquier polinomio con una variable es una función y se puede escribir en la forma\(f ( x ) = a _ { n } x ^ { n } + a _ { n - 1 } x ^ { n - 1 } + \ldots + a _ { 1 } x + a _ { 0 }\). El grado del polinomio es el mayor exponente de todos los términos.
- Utilice la notación de funciones para agilizar el proceso de evaluación. Sustituir el valor o expresión dentro de los paréntesis por cada instancia de la variable.
- La notación\((f+g)(x)\) indica que debemos agregar\(f(x)+g(x)\).
- La notación\((f−g)(x)\) indica que debemos restar\(f(x)−g(x)\).
- La notación\((f⋅g)(x)\) indica que debemos multiplicar\(f(x)g(x)\).
- La notación\((f/g)(x)\) indica que debemos dividir\(\frac{f(x)}{g(x)}\), donde\(g(x)≠0\).
- El dominio de la función que resulta de estas operaciones aritméticas es la intersección del dominio de cada función. El dominio de un cociente se restringe aún más a valores que no evalúan a cero en el denominador.
Ejercicio\(\PageIndex{4}\)
Evaluar.
- Dado\(f(x)=x^{2}−10x+3\), encontrar\(f(−3), f(0)\), y\(f(5)\).
- Dado\(f(x)=2x^{2}−x+9\), encontrar\(f(−1), f(0)\), y\(f(3)\).
- Dado\(g(x)=x^{3}−x^{2}+x+7\), encontrar\(g(−2), g(0)\), y\(g(3)\).
- Dado\(g(x)=x^{3}−2x+5\), encontrar\(g(−5), g(0)\), y\(g(3)\).
- Dado\(s(t)=5t^{4}−t^{2}+t−3\), encontrar\(s(−1), s(0)\), y\(s(2)\).
- Dado\(p(n)=n^{4}−10n^{2}+9\), encontrar\(p(−3), p(−1)\), y\(p(2)\).
- Dado\(f(x)=x^{6}−64\), encontrar\(f(−2), f(−1)\), y\(f(0)\).
- Dado\(f(x)=x^{6}−x^{3}+3\), encontrar\(f(−2), f(−1)\), y\(f(0)\).
- Dado\(f(x)=x^{2}−2x−1\), encontrar\(f(2t)\) y\(f(2t−1)\).
- Dado\(f(x)=x^{2}−2x+4\), encontrar\(f(−3t)\) y\(f(2−3t)\).
- Dado\(g(x)=2x^{2}+3x−1\), encontrar\(g(−5a)\) y\(g(5−2x)\).
- Dado\(g(x)=3x^{2}−5x+4\), encontrar\(g(−4u)\) y\(g(3x−1)\).
- Dado\(f(x)=x^{3}−1\), encontrar\(f(2a)\) y\(f(x−2)\).
- Dado\(f(x)=x^{3}−x+1\), encontrar\(f(−3x)\) y\(f(2x+1)\).
- Dado\(g(x)=x^{3}+x^{2}−1\), encontrar\(g(x^{2})\) y\(g(x−4)\).
- Dado\(g(x)=2x^{3}−x+1\), encontrar\(g(−2x^{3})\) y\(g(3x−1)\).
- Contestar
-
1. \(f ( - 3 ) = 42 ; f ( 0 ) = 3 ; f ( 5 ) = - 22\)
3. \(g ( - 2 ) = - 7 ; g ( 0 ) = 7 ; g ( 3 ) = 28\)
5. \(s ( - 1 ) = 0 ; s ( 0 ) = - 3 ; s ( 2 ) = 75\)
7. \(f ( - 2 ) = 0 ; f ( - 1 ) = - 63 ; f ( 0 ) = - 64\)
9. \(f ( 2 t ) = 4 t ^ { 2 } - 4 t - 1 : f ( 2 t - 1 ) = 4 t ^ { 2 } - 8 t + 2\)
11. \(g ( - 5 a ) = 50 a ^ { 2 } - 15 a - 1 ; g ( 5 - 2 x ) = 8 x ^ { 2 } - 46 x + 64\)
13. \(f ( 2 a ) = 8 a ^ { 3 } - 1 ; f ( x - 2 ) = x ^ { 3 } - 6 x ^ { 2 } + 12 x - 9\)
15. \(g \left( x ^ { 2 } \right) = x ^ { 6 } + x ^ { 4 } - 1 ; g ( x - 4 ) = x ^ { 3 } - 11 x ^ { 2 } + 40 x - 49\)
Ejercicio\(\PageIndex{5}\)
Dada la función calcular\(f(x+h)\).
- \(f(x)=5x−3\)
- \(f(x)=x^{2}−1\)
- \(f(x)=x^{3}−8\)
- \(f(x)=x^{4}\)
- Contestar
-
1. \(f ( x + h ) = 5 x + 5 h - 3\)
3. \(f ( x + h ) = x ^ { 3 } + 3 h x ^ { 2 } + 3 h ^ { 2 } x + h ^ { 3 } - 8\)
Ejercicio\(\PageIndex{6}\)
Dada la gráfica de la función polinómica\(f\) encontrar los valores de la función.
1. Encontrar\(f(0), f(1)\), y\(f(2)\).
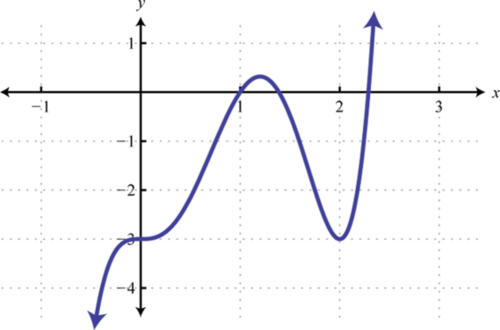
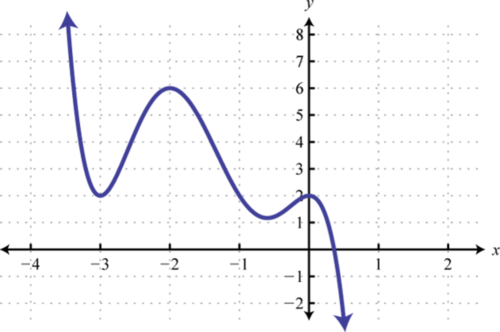
2. Encontrar\(f(−1), f(0)\), y\(f(1)\).
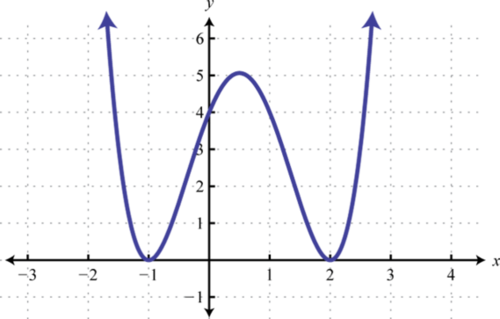
3. Encontrar\(f(−2), f(−1)\), y\(f(0)\).
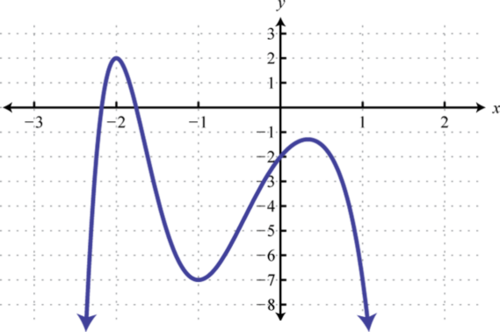
4. Encontrar\(f(−3), f(−2)\), y\(f(0)\).
5. Un proyectil se lanza hacia arriba desde el suelo a una velocidad de\(48\) pies por segundo. Escribe una función que modele la altura del proyectil y utilízala para calcular la altura cada\(1/2\) segundo después del lanzamiento. Esboce una gráfica que muestre la altura del proyectil con respecto al tiempo.
6. Un objeto se lanza hacia arriba desde una plataforma\(48\) de pies a una velocidad de\(32\) pies por segundo. Escriba una función que modele la altura del objeto y utilícela para calcular la altura cada\(1/2\) segundo después de lanzar el objeto. Esboce una gráfica que muestre la altura del objeto con respecto al tiempo.
7. Un objeto se deja caer desde un puente\(128\) de pie. Escribe una función que modele la altura del objeto, y utilízala para calcular la altura en\(1\) segundos y\(2\) segundos después de que se haya caído.
8. Un objeto se deja caer de un edificio\(500\) de pies. Escribe una función que modele la altura del objeto, y utilízala para calcular la distancia que cae el objeto en el\(1\) st segundo,\(2\) nd segundo y\(3\) rd segundo.
9. Se dispara una bala en línea recta al aire a\(320\) metros por segundo. Ignorando los efectos de la fricción del aire, escriba una función que modele la altura de la bala, y utilícela para calcular la altura de la bala\(1\) minuto después de que fue disparada al aire.
10. Se deja caer un libro desde una altura de\(10\) metros. Escribe una función que dé la altura del libro, y úsalo para determinar hasta qué punto caerá en\(1 \frac{1}{4}\) segundos.
- Contestar
-
1. \(f ( 0 ) = - 3 ; f ( 1 ) = 0 ; f ( 2 ) = - 3\)
3. \(f ( - 2 ) = 2 ; f ( - 1 ) = - 7 ; f ( 0 ) = - 2\)
5. \(h ( t ) = - 16 t ^ { 2 } + 48 t\)
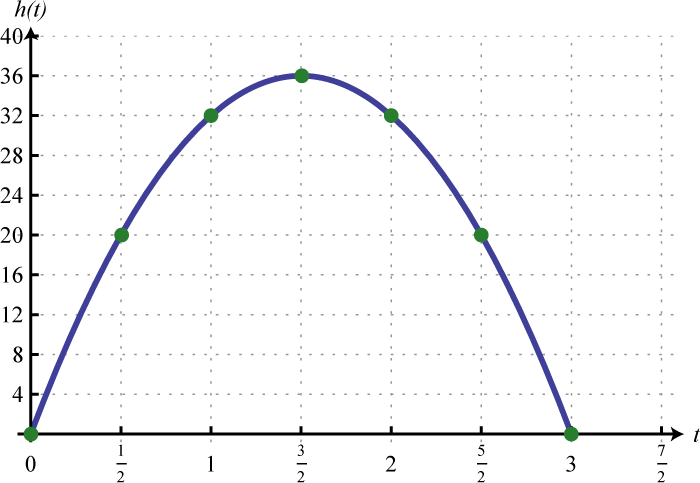
Figura\(\PageIndex{11}\) 7. \(h ( t ) = - 16 t ^ { 2 } + 128\); Al\(1\) segundo la altura del objeto es\(112\) pies y en\(2\) segundos su altura es\(64\) pies.
9. \(h ( t ) = - 4.9 t ^ { 2 } + 320 t ; 1,560\)metros
Ejercicio\(\PageIndex{7}\)
Dadas funciones\(f\) y\(g\), encontrar\((f+g)\) y\((f-g)\).
- \(f(x)=5x−3, g(x)=4x−1\)
- \(f(x)=3x+2, g(x)=7x−5\)
- \(f(x)=2−3x, g(x)=1−x\)
- \(f(x)=8x−5, g(x)=−7x+4\)
- \(f(x)=x^{2}−3x+2, g(x)=x^{2}+4x−7\)
- \(f(x)=2x^{2}+x−3, g(x)=x^{2}−x+4\)
- \(f(x)=x^{2}+5x−3, g(x)=6x+11\)
- \(f(x)=9x+5, g(x)=2x^{2}−5x+4\)
- \(f(x)=9x^{2}−1, g(x)=x^{2}+5x\)
- \(f(x)=10x^{2}, g(x)=5x^{2}−8\)
- \(f(x)=8x^{3}+x−4, g(x)=4x^{3}+x^{2}−1\)
- \(f(x)=x^{3}−x^{2}+x+1, g(x)=x^{3}−x^{2}−x−1\)
- Contestar
-
1. \(( f + g ) ( x ) = 9 x - 4 ; ( f - g ) ( x ) = x - 2\)
3. \(( f + g ) ( x ) = - 4 x + 3 ; ( f - g ) ( x ) = - 2 x + 1\)
5. \(( f + g ) ( x ) = 2 x ^ { 2 } + x - 5 ; ( f - g ) ( x ) = - 7 x + 9\)
7. \(( f + g ) ( x ) = x ^ { 2 } + 11 x + 8 ; ( f - g ) ( x ) = x ^ { 2 } - x - 14\)
9. \(( f + g ) ( x ) = 10 x ^ { 2 } + 5 x - 1 ; ( f - g ) ( x ) = 8 x ^ { 2 } - 5 x - 1\)
11. \(\begin{array} { l } { ( f + g ) ( x ) = 12 x ^ { 3 } + x ^ { 2 } + x - 5 } \\ { ( f - g ) ( x ) = 4 x ^ { 3 } - x ^ { 2 } + x - 3 } \end{array}\)
Ejercicio\(\PageIndex{8}\)
Dado\(f ( x ) = x ^ { 3 } + 2 x ^ { 2 } - 8\) y\(g ( x ) = 2 x ^ { 2 } - 3 x + 5\), evaluar lo siguiente.
- \((f+g)(−2)\)
- \((f+g)(3)\)
- \((f−g)(−2)\)
- \((f−g)(3)\)
- \((g−f)(−2)\)
- \((g−f)(3)\)
- \((f+f)(1)\)
- \((g+g)(−1)\)
- Contestar
-
1. \(11\)
3. \(-27\)
5. \(27\)
7. \(-10\)
Ejercicio\(\PageIndex{9}\)
Dadas las gráficas de\(f\) y\(g\), evaluar lo siguiente.

- \((f+g)(−4)\)
- \((f−g)(−4)\)
- \((f+g)(−2)\)
- \((f−g)(−2)\)
- \((f+g)(0)\)
- \((f−g)(0)\)
- Contestar
-
1. \(-4\)
3. \(1\)
5. \(-2\)
Ejercicio\(\PageIndex{10}\)
Dado\(f\) y\(g\), encontrar\(f⋅g\).
- \(f(x)=5x, g(x)=x−3\)
- \(f(x)=x−4, g(x)=6x\)
- \(f(x)=2x−3, g(x)=3x+4\)
- \(f(x)=5x−1, g(x)=2x+1\)
- \(f(x)=3x+4, g(x)=3x−4\)
- \(f(x)=x+5, g(x)=x−5\)
- \(f(x)=x−2, g(x)=x^{2}−3x+2\)
- \(f(x)=2x−3, g(x)=x^{2}+2x−1\)
- \(f(x)=2x^{2}, g(x)=x^{2}−7x+5\)
- \(f(x)=5x^{3}, g(x)=x^{2}−3x−1\)
- \(f(x)=x^{2}−3x−2, g(x)=2x^{2}−x+3\)
- \(f(x)=x^{2}+x−1, g(x)=x^{2}−x+1\)
- Contestar
-
1. \(( f \cdot g ) ( x ) = 5 x ^ { 2 } - 15 x\)
3. \(( f \cdot g ) ( x ) = 6 x ^ { 2 } - x - 12\)
5. \(( f \cdot g ) ( x ) = 9 x ^ { 2 } - 16\)
7. \(( f \cdot g ) ( x ) = x ^ { 3 } - 5 x ^ { 2 } + 8 x - 4\)
9. \(( f \cdot g ) ( x ) = 2 x ^ { 4 } - 14 x ^ { 3 } + 10 x ^ { 2 }\)
11. \(( f \cdot g ) ( x ) = 2 x ^ { 4 } - 7 x ^ { 3 } + 2 x ^ { 2 } - 7 x - 6\)
Ejercicio\(\PageIndex{11}\)
Dado\(f\) y\(g\), encontrar\(f/g\). (Supongamos que todas las expresiones en el denominador son distintas de cero.)
- \(f ( x ) = 36 x ^ { 3 } - 16 x ^ { 2 } - 8 x , g ( x ) = 4 x\)
- \(f ( x ) = 2 x ^ { 3 } - 6 x ^ { 2 } + 10 x , g ( x ) = 2 x\)
- \(f ( x ) = 20 x ^ { 7 } - 15 x ^ { 5 } + 5 x ^ { 3 } , g ( x ) = 5 x ^ { 3 }\)
- \(f ( x ) = 9 x ^ { 6 } + 12 x ^ { 4 } - 3 x ^ { 2 } , g ( x ) = 3 x ^ { 2 }\)
- \(f ( x ) = x ^ { 3 } + 4 x ^ { 2 } + 3 x - 2 , g ( x ) = x + 2\)
- \(f ( x ) = x ^ { 3 } - x ^ { 2 } - 10 x + 12 , g ( x ) = x - 3\)
- \(f ( x ) = 6 x ^ { 3 } - 13 x ^ { 2 } + 36 x - 45 , g ( x ) = 2 x - 3\)
- \(f ( x ) = 6 x ^ { 3 } - 11 x ^ { 2 } + 15 x - 4 , g ( x ) = 3 x - 1\)
- \(f ( x ) = 3 x ^ { 3 } - 13 x ^ { 2 } - x + 8 , g ( x ) = 3 x + 2\)
- \(f ( x ) = 5 x ^ { 3 } - 16 x ^ { 2 } + 13 x - 6 , g ( x ) = 5 x - 1\)
- Contestar
-
1. \(( f / g ) ( x ) = 9 x ^ { 2 } - 4 x - 2\)
3. \(( f / g ) ( x ) = 4 x ^ { 4 } - 3 x ^ { 2 } + 1\)
5. \(( f / g ) ( x ) = x ^ { 2 } + 2 x - 1\)
7. \(( f / g ) ( x ) = 3 x ^ { 2 } - 2 x + 15\)
9. \(( f / g ) ( x ) = x ^ { 2 } - 5 x + 3 + \frac { 2 } { 3 x + 2 }\)
Ejercicio\(\PageIndex{12}\)
Dado\(f ( x ) = 25 x ^ { 4 } + 10 x ^ { 3 } - 5 x ^ { 2 }\) y\(g(x) = 5x^{2}\) evaluar lo siguiente.
- \((f⋅g)(−1)\)
- \((f⋅g)(1)\)
- \((f/g)(−2)\)
- \((f/g)(−3)\)
- \((g⋅f)(0)\)
- \((g/f)(1)\)
- \((g⋅g)(−1)\)
- \((f⋅f)(−1)\)
- Contestar
-
1. \(50\)
3. \(15\)
5. \(0\)
7. \(25\)
Ejercicio\(\PageIndex{13}\)
Dadas las gráficas de\(f\) y\(g\) evaluar lo siguiente.

1. \((f⋅g)(3)\)
2. \((f⋅g)(5)\)
3. \((f/g)(5)\)
4. \((f/g)(3)\)
5. \((f⋅g)(1)\)
6. \((f/g)(1)\)
- Contestar
-
1. \(-2\)
3. \(0\)
5. \(4\)
Ejercicio\(\PageIndex{14}\)
Dado\(f ( x ) = 5 x ^ { 3 } - 15 x ^ { 2 } + 10 x , g ( x ) = x ^ { 2 } - x + 3\), y\(h(x)=-5x\), encuentra lo siguiente. (Supongamos que todas las expresiones en el denominador son distintas de cero.)
- \((f−g)(x)\)
- \((g−f)(x)\)
- \((g⋅h)(x)\)
- \((f/h)(x)\)
- \((h+g)(x)\)
- \((h⋅f)(x)\)
- \((g/h)(2)\)
- \((g−h)(−3)\)
- El ingreso en dólares por la venta de reproductores MP3 viene dado por la función\(R(n)=125n−0.15n^{2}\), donde\(n\) representa el número de unidades vendidas\((0≤n<833)\). El costo en dólares de producir los reproductores MP3 viene dado por la fórmula\(C(n)=1200+42n\) donde\(n\) representa el número de unidades producidas. Escribe una función que modele el beneficio de producir y vender reproductores\(n\) MP3. Utilice la función para determinar el beneficio generado por la producción y venta de reproductores\(225\) MP3. Recordemos que el beneficio equivale a ingresos menos costos.
- El radio interior de una arandela\(\frac{1}{2}\) es el del radio exterior.
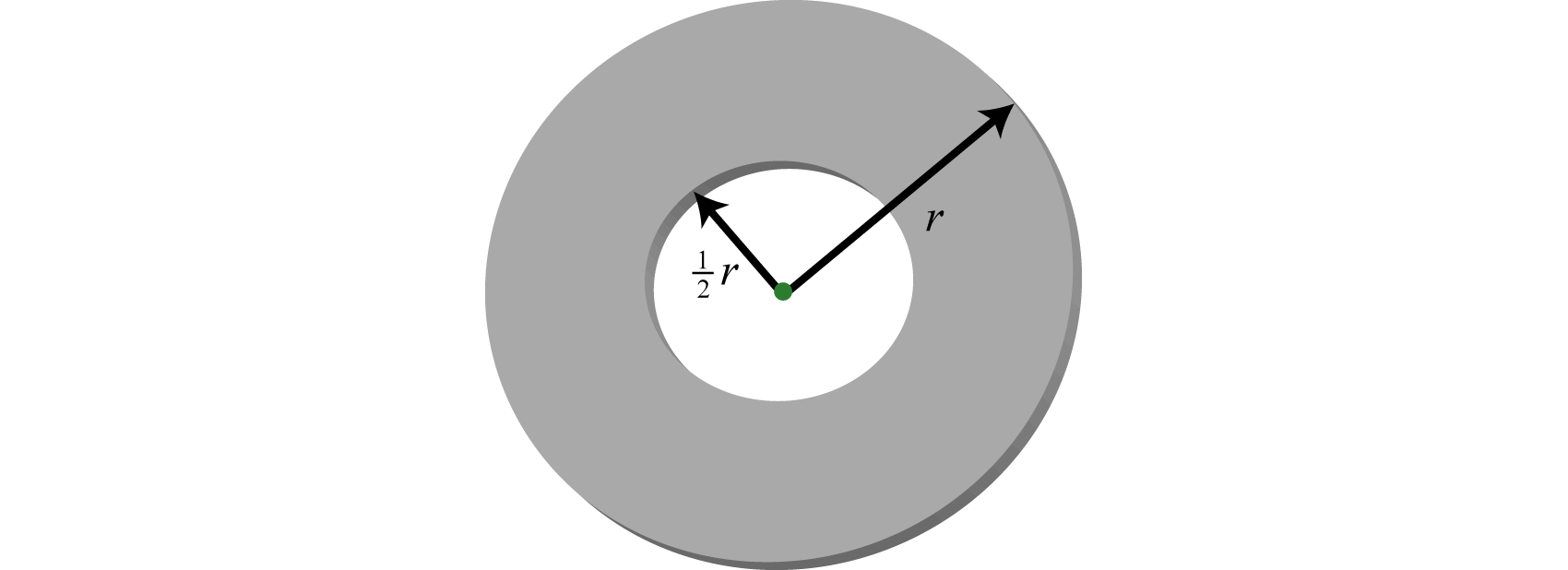
- Contestar
-
1. \(( f - g ) ( x ) = 5 x ^ { 3 } - 16 x ^ { 2 } + 11 x - 3\)
3. \(( g \cdot h ) ( x ) = - 5 x ^ { 3 } + 5 x ^ { 2 } - 15 x\)
5. \(( h + g ) ( x ) = x ^ { 2 } - 6 x + 3\)
7. \(( g / h ) ( 2 ) = - \frac { 1 } { 2 }\)
9. \(P ( n ) = - 0.15 n ^ { 2 } + 83 n - 1200 ; \$ 9,881.25\)
Ejercicio\(\PageIndex{15}\)
Utilice las gráficas de\(f\) y\(g\) para graficar\(f+g\). También, dar el dominio de\(f+g\).
1.

2.

3.

4.

5.
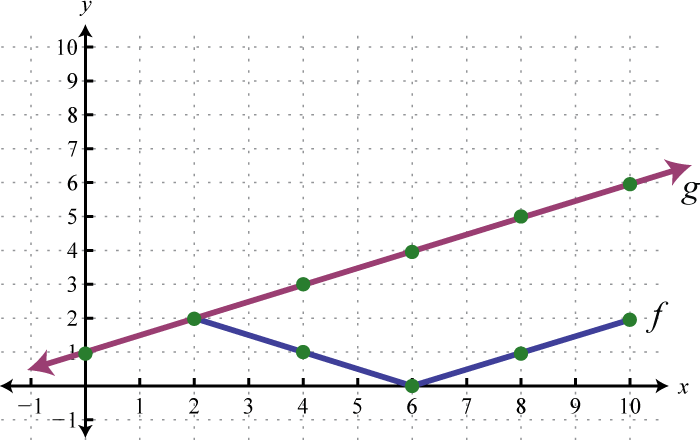
6.
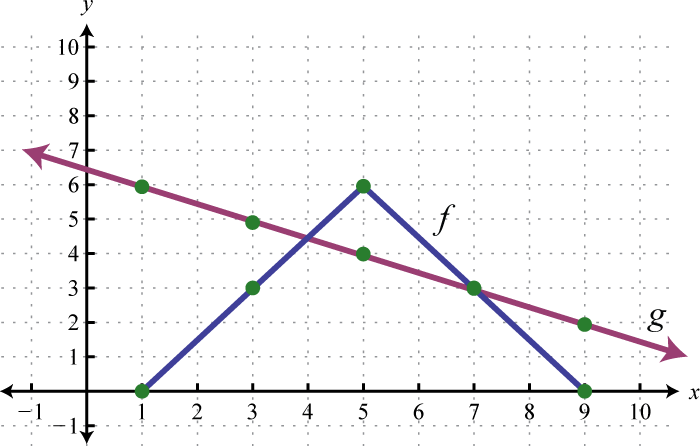
7.

8.

9.

10.

- Contestar
-
1. \([2,8]\)

Figura\(\PageIndex{25}\) 3. \([0,10]\)

Figura\(\PageIndex{26}\) 5. \([2,10]\)

Figura\(\PageIndex{27}\) 7. \([ - 2 , \infty )\)
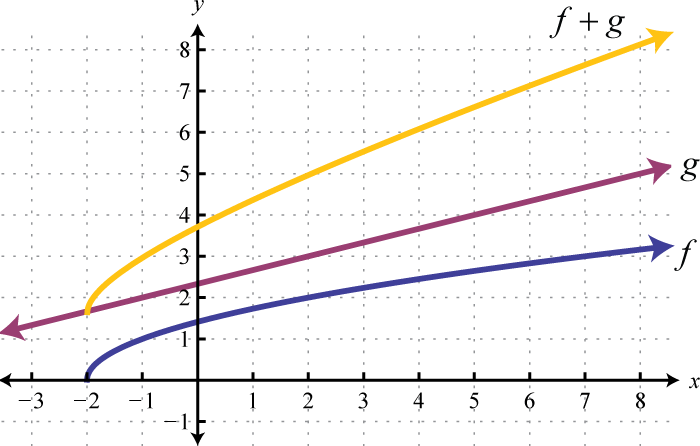
Figura\(\PageIndex{28}\) 9. \(( - \infty , \infty )\)

Figura\(\PageIndex{29}\)
Ejercicio\(\PageIndex{16}\)
- ¿Qué operaciones aritméticas en funciones son conmutativas? Explique.
- Explore formas en las que podemos agregar funciones gráficamente si resultan ser negativas.
- Contestar
-
1. La respuesta puede variar
Notas al pie
1 Agregar funciones como lo indica la notación:\((f + g) (x) = f (x) + g (x) \).
2 Restar funciones como indica la notación:\((f − g) (x) = f (x) − g (x)\).
3 Multiplicar funciones como lo indica la notación:\((f ⋅ g) (x) = f (x) ⋅ g (x)\).
4 Dividir funciones como lo indica la notación:\((f /g) (x) = \frac{f(x)}{ g(x)}\), donde\(g (x) ≠ 0\).


