4.2: Factorización de polinomios

Objetivos de aprendizaje

• Determinar el mayor factor común (GCF) de los monomios.
• Factorizar el GCF de un polinomio.
• Factorizar un polinomio de cuatro términos por agrupación.
• Binomios especiales de factor.

Determinación del GCF de los Monomios

El proceso de escribir un número o expresión como producto se denomina factoring ⁵. Si escribimos el monomio$8x^{7}=2x^{5}⋅4x^{2}$, decimos que el producto$2x^{5}⋅4x^{2}$ es una factorización ⁶ de$8x^{7}$ y eso$2x^{5}$ y$4x^{2}$ son factores ⁷. Por lo general, hay muchas formas de factorizar un monomio. Algunas factorizaciones de$8x^{7}$ seguimiento:

$\left. \begin{aligned} 8 x ^ { 7 } & = 2 x ^ { 5 } \cdot 4 x ^ { 2 } \\ 8 x ^ { 7 } & = 8 x ^ { 6 } \cdot x \\ 8 x ^ { 7 } & = 2 x \cdot 2 x ^ { 2 } \cdot 2 x ^ { 4 } \end{aligned} \right\} \quad \color{Cerulean} { Factorizations\: of \:} 8 x ^ { 7 }$

Dados dos o más monomios, será útil encontrar el mayor factor monomial común (GCF) ⁸ de cada uno. El GCF de los monomios es el producto de los factores variables comunes y el GCF de los coeficientes.

Ejemplo$\PageIndex{1}$

Encuentre el GCF de$25x^{7}y^{2}z$ y$15x^{3}y^{4}z^{2}$.

Solución

Comience por encontrar el GCF de los coeficientes. En este caso,$25=5⋅5$ y$15=3⋅5$. Debe quedar claro que

$\operatorname { GCF } ( 25,15 ) = 5$

A continuación, determinar los factores variables comunes con los exponentes más pequeños.

$25 x ^ { 7 } \color{Cerulean}{y ^ { 2 } z} \quad \color{black}{\text { and} } \quad 15\color{Cerulean}{ x ^ { 3} } \color{black}{y ^ { 4 }} z ^ { 2 }$

Los factores variables comunes son$x^{3}, y^{2}$, y$z$. Por lo tanto, dados los dos monomios,

$\mathrm { GCF } = 5 x ^ { 3 } y ^ { 2 } z$

Respuesta:

$5x^{3}y^{2}z$

Cabe señalar que el GCF divide ambas expresiones de manera uniforme.

$\frac { 25 x ^ { 7 } y ^ { 2 } z } {\color{Cerulean}{ 5 x ^ { 3 } y ^ { 2 } z} }\color{black}{ =} 5 x ^ { 4 } \quad \text { and } \quad \frac { 15 x ^ { 3 } y ^ { 4 } z ^ { 2 } } {\color{Cerulean}{ 5 x ^ { 3 } y ^ { 2 } z} }\color{black}{ =} 3 y ^ { 2 } z$

Además, podemos escribir lo siguiente:

$25 x ^ { 7 } y ^ { 2 } z = \color{Cerulean}{5 x ^ { 3 } y ^ { 2 } z}\color{black}{ \cdot} 5 x ^ { 4 } \quad \text { and } \quad 15 x ^ { 3 } y ^ { 4 } z ^ { 2 } = \color{Cerulean}{5 x ^ { 3 } y ^ { 2 } z}\color{black}{ \cdot} 3 y ^ { 2 } z$

Los factores$5x^{4}$ y no$3y^{2}z$ comparten otros factores monomiales comunes que no sean$1$; son relativamente primos ⁹.

Ejemplo$\PageIndex{2}$

Determinar el GCF de las siguientes tres expresiones:$12a^{5}b^{2}(a+b)^{5}, 60a^{4}b^{3}c (a+b)^{3}$, y$24a^{2}b^{7}c^{3}(a+b)^{2}$.

Solución

Comience por encontrar el GCF de los coeficientes. Para ello, determinar la factorización prima de cada uno y luego multiplicar los factores comunes con los exponentes más pequeños.

$\begin{array} { l } { 12 = 2 ^ { 2 } \cdot 3 } \\ { 60 = 2 ^ { 2 } \cdot 3 \cdot 5 } \\ { 24 = 2 ^ { 3 } \cdot 3 } \end{array}$

Por lo tanto, el GCF de los coeficientes de los tres monomios es

$\operatorname { GCF } ( 12,60,24 ) = 2 ^ { 2 } \cdot 3 = 12$

A continuación, determinar los factores comunes de las variables.

$12a^{5}\color{Cerulean}{b^{2}}\color{black}{(}a+b)^{5}$y$60a^{4}b^{3}c(a+b)^{3}$ y$24\color{Cerulean}{a^{2}}\color{black}{b^{7}}c^{3}\color{Cerulean}{(a+b)^{2}}$

Los factores variables en común son$a^{2}, b^{2}$, y$(a+b)^{2}$. Por lo tanto,

$\mathrm { GCF } = 12 \cdot a ^ { 2 } \cdot b ^ { 2 } \cdot ( a + b ) ^ { 2 }$

Tenga en cuenta que la variable no$c$ es común a las tres expresiones y por lo tanto no se incluye en el GCF.

Contestar

$12a^{2}b^{2}(a+b)^{2}$

Factorización del GCF

La aplicación de la propiedad distributiva es la clave para multiplicar polinomios. Por ejemplo,

$\begin{aligned} \color{Cerulean}{6 x y ^ { 2} }\color{black}{ (} 2 x y + 1 ) & = \color{Cerulean}{6 x y ^ { 2} }\color{black}{ \cdot} 2 x y + \color{Cerulean}{6 x y ^ { 2} }\color{black}{ \cdot} 1 \quad \color{Cerulean} { Multiplying } \\ & = 12 x ^ { 2 } y ^ { 3 } + 6 x y ^ { 2 } \end{aligned}$

El proceso de factorizar un polinomio implica aplicar la propiedad distributiva a la inversa para escribir cada polinomio como producto de factores polinomiales.

$\begin{array} { c c } { \color{Cerulean}{a}\color{black}{ (} b + c ) = \color{Cerulean}{a}\color{black}{ b} + \color{Cerulean}{a}\color{black}{ c} } & { \color{Cerulean} { Multiplying } } \\ {\color{Cerulean}{ a}\color{black}{ b} + \color{Cerulean}{a}\color{black}{ c} = \color{Cerulean}{a}\color{black}{ (} b + c ) } & { \color{Cerulean} { Factoring } } \end{array}$

Considere factorizar el resultado del ejemplo de apertura:

$\begin{aligned} 12 x ^ { 2 } y ^ { 3 } + 6 x y ^ { 2 } & = \color{Cerulean}{6 x y ^ { 2} }\color{black}{ \cdot} 2 x y +\color{Cerulean}{ 6 x y ^ { 2} }\color{black}{ \cdot} 1 \quad \color{Cerulean}{Factoring} \\ & =\color{Cerulean}{ 6 x y ^ { 2} } \color{black}{(}\quad ?\quad ) \\ & = \color{Cerulean}{6 x y ^ { 2} }\color{black}{ (} 2 x y + 1 ) \end{aligned}$

Vemos que la propiedad distributiva nos permite escribir el polinomio$12x^{2}y^{3} +  6xy^{2}$ como producto de los dos factores$6xy^{2}$ y$(2xy+1)$. Obsérvese que en este caso,$6x^{2}y$ es el GCF de los términos del polinomio.

$\operatorname { GCF } \left( 12 x ^ { 2 } y ^ { 3 } , 6 x y ^ { 2 } \right) = 6 x y ^ { 2 }$

Factorizar el mayor factor común (GCF) ¹⁰ de un polinomio implica reescribirlo como un producto donde un factor es el GCF de todos sus términos.

$\left. \begin{array} { c } { 8 x ^ { 3 } + 4 x ^ { 2 } - 16 x = \color{Cerulean}{4 x} \color{black}{\left( 2 x ^ { 2 } + x - 4 \right) }} \\ { 9 a b ^ { 2 } - 18 a ^ { 2 } b - 3 a b =\color{Cerulean}{ 3 a b}\color{black}{ (} 3 b - 6 a - 1 ) } \end{array} \right\} \quad \color{Cerulean}{Factoring\:out\:the\:GCF}$

Para factorizar el GCF de un polinomio, primero determinamos el GCF de todos sus términos. Entonces podemos dividir cada término del polinomio por este factor como medio para determinar el factor restante después de aplicar la propiedad distributiva a la inversa.

Ejemplo$\PageIndex{3}$

Factorizar el GCF:$18x^{7}−30x^{5}+6x^{3}$.

Solución

En este caso, el$GCF(18, 30, 6) = 6$, y el factor variable común con el exponente más pequeño es$x^{3}$. El GCF del polinomio es$6x^{3}$.

$18 x ^ { 7 } - 30 x ^ { 5 } + 6 x ^ { 3 } = \color{Cerulean}{6 x ^ { 3} }\color{black}{ (} \quad ?\quad )$

El factor faltante se puede encontrar dividiendo cada término de la expresión original por el GCF.

$\frac { 18 x ^ { 7 } } { \color{Cerulean}{6 x ^ { 3} } } \color{black}{=} 3 x ^ { 4 } \quad \frac { - 30 x ^ { 5 } } { \color{Cerulean}{6 x ^ { 3} } } \color{black}{=} - 5 x ^ { 2 } \quad \frac { + 6 x ^ { 3 } } {\color{Cerulean}{ 6 x ^ { 3} } } \color{black}{=} + 1$

Aplicar la propiedad distributiva (a la inversa) utilizando los términos encontrados en el paso anterior.

$18 x ^ { 7 } - 30 x ^ { 5 } + 6 x ^ { 3 } = \color{Cerulean}{6 x ^ { 3} }\color{black}{ \left( 3 x ^ { 4 } - 5 x ^ { 2 } + 1 \right)}$

Si el GCF es el mismo que uno de los términos, entonces, después de factorizar el GCF,$1$ quedará un término constante. La importancia de recordar el término constante se hace evidente al realizar la comprobación utilizando la propiedad distributiva.

$\begin{aligned} \color{Cerulean}{6 x ^ { 3} }\color{black}{ \left( 3 x ^ { 4 } - 5 x ^ { 2 } + 1 \right)} & = \color{Cerulean}{6 x ^ { 3} }\color{black}{ \cdot} 3 x ^ { 4 } - \color{Cerulean}{6 x ^ { 3} }\color{black}{ \cdot} 5 x ^ { 2 } +\color{Cerulean}{ 6 x ^ { 3} } \color{black}{\cdot} 1 \\ & = 18 x ^ { 7 } - 30 x ^ { 5 } + 6 x ^ { 3 } \quad\color{Cerulean}{✓}\end{aligned}$

Contestar

$6 x ^ { 3 } \left( 3 x ^ { 4 } - 5 x ^ { 2 } + 1 \right)$

Ejemplo$\PageIndex{4}$

Factorizar el GCF:$27x^{5}y^{5}z+54x^{5}yz−63x^{3}y^{4}$.

Solución

El GCF de los términos es$9x^{3}y$. El último término no tiene un factor variable de$z$, y por lo tanto$z$ no puede formar parte del mayor factor común. Si dividimos cada término por$9x^{3}y$, obtenemos

$\frac { 27 x ^ { 5 } y ^ { 5 } z } { \color{Cerulean}{9 x ^ { 3 } y} }\color{black}{ =} 3 x ^ { 2 } y ^ { 4 } z \quad \frac { 54 x ^ { 5 } y z } { \color{Cerulean}{9 x ^ { 3 } y} }\color{black}{ =} 6 x ^ { 2 } z \quad \frac { - 63 x ^ { 3 } y ^ { 4 } } { \color{Cerulean}{9 x ^ { 3 } y} }\color{black}{ =} - 7 y ^ { 3 }$

y puede escribir

$\begin{aligned} 27 x ^ { 5 } y ^ { 5 } z + 54 x ^ { 5 } y z - 63 x ^ { 3 } y ^ { 4 } & = \color{Cerulean}{9 x ^ { 3 } y}\color{black}{ (} \quad ?\quad ) \\ & = 9 x ^ { 3 } y \left( 3 x ^ { 2 } y ^ { 4 } z + 6 x ^ { 2 } z - 7 y ^ { 3 } \right) \end{aligned}$

Respuesta:

$9 x ^ { 3 } y \left( 3 x ^ { 2 } y ^ { 4 } z + 6 x ^ { 2 } z - 7 y ^ { 3 } \right)$

Ejercicio$\PageIndex{1}$

Factorizar el GCF:$12 x ^ { 3 } y ^ { 4 } - 6 x ^ { 2 } y ^ { 3 } - 3 x y ^ { 2 }$

Contestar

$3 x y ^ { 2 } \left( 4 x ^ { 2 } y ^ { 2 } - 2 x y - 1 \right)$

www.youtube.com/V/frniljz10xy

Por supuesto, no todos los polinomios con coeficientes enteros pueden ser factorizados como un producto de polinomios con coeficientes enteros distintos de$1$ y en sí mismo. Si este es el caso, entonces decimos que se trata de un polinomio primo ¹¹. Por ejemplo, un factor lineal como$10x−9$ es primo. Sin embargo, se puede factorizar de la siguiente manera:

$10 x - 9 = x \left( 10 - \frac { 9 } { x } \right) \quad \text { or } \quad 10 x - 9 = 5 \left( 2 x - \frac { 9 } { 5 } \right)$

Si se factoriza una x, el factor resultante no es un polinomio. Si se factoriza alguna constante, el factor polinómico resultante no tendrá coeficientes enteros. Además, algunos factores lineales no son primos. Por ejemplo,

$5x−10=5(x−2)$

En general, cualquier factor lineal de la forma$ax+b$, donde$a$ y$b$ son números enteros primos relativamente, es primo.

Factorización por Agrupación

En esta sección, esbozamos una técnica para factorizar polinomios con cuatro términos. Primero, revisar un ejemplo preliminar donde los términos tienen un factor binomial común.

Ejemplo$\PageIndex{5}$

Factor:$7x(3x−2)−(3x−2)$.

Solución

Empezar por reescribir el segundo término$−(3x−2)$ como$−1(3x−2)$. A continuación, considere$(3x−2)$ como un factor binomial común y factorizarlo de la siguiente manera:

$\begin{aligned} 7 x ( 3 x - 2 ) - ( 3 x - 2 ) & = 7 x \color{Cerulean}{( 3 x - 2 )}\color{black}{ -} 1 \color{Cerulean}{( 3 x - 2 )} \\ & =\color{Cerulean}{ ( 3 x - 2 )}\color{black}{ (}\quad ?\quad ) \\ & = ( 3 x - 2 ) ( 7 x - 1 ) \end{aligned}$

Respuesta:

$(3x−2)(7x−1)$

La factorización por agrupación ¹² es una técnica que nos permite factorizar polinomios con cuatro términos en un producto de binomios. Esto implica un paso intermedio donde se factorizará un factor binomial común. Por ejemplo, deseamos factorizar

$3x^{3}−12x^{2}+2x−8$

Comience agrupando los dos primeros términos y los dos últimos términos. Luego factorizar el GCF de cada agrupación:

Figura$\PageIndex{1}$

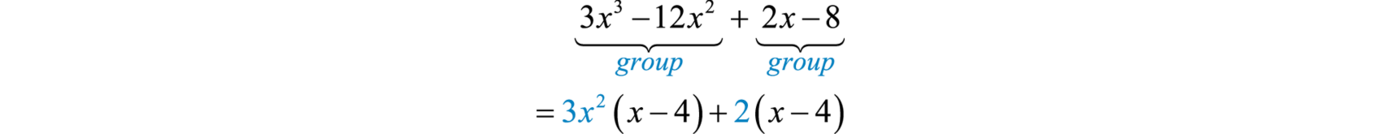
De esta forma, el polinomio es un binomio con un factor binomial común,$(x−4)$.

$\begin{array} { c } { = ( x - 4 ) ( \quad?\quad ) } \\ { = ( x - 4 ) \left( \color{Cerulean}{3 x ^ { 2 } + 2} \right) } \end{array}$

Por lo tanto,

$3 x ^ { 3 } - 12 x ^ { 2 } + 2 x - 8 = ( x - 4 ) \left( 3 x ^ { 2 } + 2 \right)$

Podemos verificar multiplicando.

$\begin{aligned} ( x - 4 ) \left( 3 x ^ { 2 } + 2 \right) & = 3 x ^ { 3 } + 2 x - 12 x ^ { 2 } - 8 \\ & = 3 x ^ { 3 } - 12 x ^ { 2 } + 2 x - 8 \end{aligned} \:\:\color{Cerulean}{✓}$

Ejemplo$\PageIndex{6}$

Factorizar por agrupación$24a^{4}−18a^{3}−20a+15$.

Solución

El GCF para el primer grupo es$6a^{3}$. Tenemos que elegir$5$ o$−5$ factorizar fuera del segundo grupo.

Figura$\PageIndex{2}$

La factorización$+5$ no resulta en un factor binomial común. Si elegimos factorizar$−5$, entonces obtenemos un factor binomial común y podemos proceder. Tenga en cuenta que al factorizar un número negativo, cambiamos los signos de los términos factorizados.

Figura$\PageIndex{3}$

Contestar

$(4a−3)(6a^{3}−5)$. Verificar multiplicando; esto se deja al lector como ejercicio.

En ocasiones debemos primero reorganizar los términos para obtener un factor común.

Ejemplo$\PageIndex{7}$

Factor$ab -2a^{2}b + a^{3} -2b^{2}$.

Solución

Simplemente factorizar el GCF del primer grupo y último grupo no produce un factor binomial común.

Figura$\PageIndex{4}$

Debemos reordenar los términos, buscando una agrupación que produzca un factor común. En este ejemplo, tenemos una agrupación viable si cambiamos los términos$a^{3}$ y$ab$.

Figura$\PageIndex{5}$

Contestar

$( a - 2 b ) \left( a ^ { 2 } + b \right)$

Ejercicio$\PageIndex{2}$

Factor$x ^ { 3 } - x ^ { 2 } y - x y + y ^ { 2 }$.

Contestar

$( x - y ) \left( x ^ { 2 } - y \right)$

www.youtube.com/v/ecdpaoz0trs

No todos los polinomios factoriables de cuatro términos se pueden factorizar con esta técnica. Por ejemplo,

$3x^{3}+5x^{2}−x+2$

Este polinomio de cuatro términos no se puede agrupar de ninguna manera para producir un factor binomial común. A pesar de ello, el polinomio no es primo y puede escribirse como producto de polinomios. Se puede factorizar de la siguiente manera:

$3x^{3}+5x^{2}−x+2=(x+2)(3x^{2}−x+1)$

Factorizar tales polinomios es algo que vamos a aprender a hacer a medida que avanzamos en nuestro estudio del álgebra. Por ahora, limitaremos nuestro intento de factorizar polinomios de cuatro términos a usar el factor mediante la técnica de agrupación.

Factorización de binomios especiales

Un binomio es un polinomio con dos términos. Comenzamos con el binomio especial llamado diferencia de cuadrados ¹³:

$a^{2}−b^{2}=(a+b)(a−b)$

Para verificar la fórmula anterior, multiplique.

$\begin{aligned} ( a + b ) ( a - b ) & = a ^ { 2 } - a b + b a - b ^ { 2 } \\ & = a ^ { 2 } \color{red}{- a b + a b}\color{black}{ -} b ^ { 2 } \\ & = a ^ { 2 } - b ^ { 2 } \end{aligned}$

Utilizamos esta fórmula para factorizar ciertos binomios especiales.

Ejemplo$\PageIndex{8}$

Factor$x^{2}-9y^{2}$.

Solución

Identificar el binomio como diferencia de cuadrados y determinar los factores cuadrados de cada término.

Figura$\PageIndex{6}$

Aquí podemos escribir

$x ^ { 2 } - 9 y ^ { 2 } = ( \color{Cerulean}{x}\color{black}{ )} ^ { 2 } - ( \color{Cerulean}{3 y}\color{black}{ )} ^ { 2 }$

Sustituir en la diferencia de cuadrados fórmula donde$a=x$ y$b=3y$.

$\begin{array} { c } { a ^ { 2 } - b ^ { 2 } = ( a + b ) ( a - b ) } \\ {\quad\quad\quad\quad \color{Cerulean}{\downarrow\quad\downarrow\quad\:\downarrow\quad\downarrow} } \\ { x ^ { 2 } - 9 y ^ { 2 } = ( x + 3 y ) ( x - 3 y ) } \end{array}$

Multiplicar para verificar:

$\begin{aligned} ( x + 3 y ) ( x - 3 y ) & = x ^ { 2 } - 3 x y + 3 y x - 9 y ^ { 2 } \\ & = x ^ { 2 } - 3 x y + 3 x y - 9 y ^ { 2 } \\ & = x ^ { 2 } - 9 y ^ { 2 }\:\:\color{Cerulean}{✓} \end{aligned}$

Contestar

$( x + 3 y ) ( x - 3 y )$

Ejemplo$\PageIndex{9}$

Factor:$x ^ { 2 } - ( 2 x - 1 ) ^ { 2 }$.

Solución

Primero, identificar esta expresión como una diferencia de cuadrados.

$x ^ { 2 } - ( 2 x - 1 ) ^ { 2 } = ( \color{Cerulean}{x}\color{black}{ )} ^ { 2 } - ( \color{Cerulean}{2 x - 1}\color{black}{ )} ^ { 2 }$

Use$a=x$ y$b=2x−1$ en la fórmula para una diferencia de cuadrados y luego simplifique.

$a ^ { 2 } - b ^ { 2 } = ( a + b ) ( a - b )$

$\begin{aligned} x ^ { 2 } - ( 2 x - 1 ) ^ { 2 } & = [ x + ( 2 x - 1 ) ] [ x - ( 2 x - 1 ) ] \\ & = ( x + 2 x - 1 ) ( x - 2 x + 1 ) \\ & = ( 3 x - 1 ) ( - x + 1 ) \end{aligned}$

Contestar

$(3x−1)(−x+1)$

Dado cualquier número real$b$, un polinomio de la forma$x^{2}+b^{2}$ es primo. Además, la suma de cuadrados ¹⁴$a^{2}+b^{2}$ no tiene un equivalente factorizado general. Se debe tener cuidado de no confundir esto con un trinomio cuadrado perfecto.

$\begin{aligned} ( a + b ) ^ { 2 } & = ( a + b ) ( a + b ) \\ & = a ^ { 2 } + a b + b a + b ^ { 2 } \\ & = a ^ { 2 } + 2 a b + b ^ { 2 } \end{aligned}$

Por lo tanto,

$(a+b)^{2}≠a^{2}+b^{2}$

Por ejemplo, la suma de cuadrados binomio$x^{2}+9$ es primo. Otros dos binomios especiales de interés son la suma ¹⁵ y la diferencia de cubos ¹⁶:

$\begin{aligned} a ^ { 3 } + b ^ { 3 } & = ( a + b ) \left( a ^ { 2 } - a b + b ^ { 2 } \right) \\ a ^ { 3 } - b ^ { 3 } & = ( a - b ) \left( a ^ { 2 } + a b + b ^ { 2 } \right) \end{aligned}$

Podemos verificar estas fórmulas multiplicando.

$\begin{aligned} ( a + b ) \left( a ^ { 2 } - a b + b ^ { 2 } \right) & = a ^ { 3 } - a ^ { 2 } b + a b ^ { 2 } + a ^ { 2 } b - a b ^ { 2 } + b ^ { 3 } \\ & = a ^ { 3 } + b ^ { 3 } \end{aligned} \:\:\color{Cerulean}{✓}$

$\begin{aligned} ( a - b ) \left( a ^ { 2 } + a b + b ^ { 2 } \right) & = a ^ { 3 } + a ^ { 2 } b + a b ^ { 2 } - a ^ { 2 } b - a b ^ { 2 } - b ^ { 3 } \\ & = a ^ { 3 } - b ^ { 3 } \end{aligned}\:\:\color{Cerulean}{✓}$

El proceso para factorizar sumas y diferencias de cubos es muy similar al de las diferencias de cuadrados. Primero identificamos$a$$b$ y luego sustituimos en la fórmula apropiada. Las fórmulas separadas para la suma y diferencia de cubos nos permiten elegir siempre$a$ y$b$ ser positivos.

Ejemplo$\PageIndex{10}$

Factor$x^{3}-8y^{3}$.

Solución

Primero, identificar este binomio como una diferencia de cubos.

Figura$\PageIndex{7}$

A continuación, identificar lo que se está poniendo en cubos.

$x ^ { 3 } - 8 y ^ { 3 } = ( \color{Cerulean}{x}\color{black}{ )} ^ { 3 } - ( \color{Cerulean}{2 y}\color{black}{ )} ^ { 3 }$

En este caso,$a=x$ y$b=2y$. Sustituir en la diferencia de cubos fórmula.

$\begin{aligned} a ^ { 3 } + b ^ { 3 } = ( a\:\: - b \:\:) \left( a ^ { 2 }\:\: + a\: \cdot\: b\:\:\: + b ^ { 2 } \right)\:\:\:\: \\ \color{Cerulean}{\downarrow\quad\:\:\:\downarrow\quad\:\:\downarrow\:\:\:\quad\:\:\downarrow\quad\downarrow\quad\:\:\:\:\:\downarrow\quad\:\:\:} \\ x ^ { 3 } - 8 y ^ { 3 } = ( x - 2 y ) \left( ( x ) ^ { 2 } + x \cdot 2 y + ( 2 y ) ^ { 2 } \right) \\ = ( x - 2 y ) \left( x ^ { 2 } + 2 x y + 4 y ^ { 2 } \right) \end{aligned}$

Podemos comprobar esta factorización multiplicando.

$\begin{aligned} ( x - 2 y ) \left( x ^ { 2 } + 2 x y + 4 y ^ { 2 } \right) & = x ^ { 3 } + 2 x ^ { 2 } y + 4 x y ^ { 2 } - 2 x ^ { 2 } y - 4 x y ^ { 2 } - 8 y ^ { 3 } \\ & = x ^ { 3 } \color{red}{+ 2 x ^ { 2 } y}\color{OliveGreen}{ + 4 x y ^ { 2 }}\color{red}{ - 2 x ^ { 2 } y}\color{OliveGreen}{ - 4 x y ^ { 2} }\color{black}{ - 8 y ^ { 3} } \\ & = x ^ { 3 } - 8 y ^ { 3 } \end{aligned}\:\:\color{Cerulean}{✓}$

Contestar

$( x - 2 y ) \left( x ^ { 2 } + 2 x y + 4 y ^ { 2 } \right)$

Puede darse el caso de que los términos del binomio tengan un factor común. Si es así, será difícil identificarlo como un binomio especial hasta que primero factorizamos el GCF.

Ejemplo$\PageIndex{11}$

Factor:$81 x ^ { 4 } y + 3 x y ^ { 4 }$.

Solución

Los términos no son cuadrados perfectos o cubos perfectos. No obstante, observe que sí tienen un factor común. Primero, factorizar el GCF,$3xy$.

$81 x ^ { 4 } y + 3 x y ^ { 4 } = 3 x y \left( 27 x ^ { 3 } + y ^ { 3 } \right)$

El factor binomial resultante es una suma de cubos con$a=3x$ y$b=y$.

$\begin{aligned} 81 x ^ { 4 } y + 3 x y ^ { 4 } & = 3 x y \left( 27 x ^ { 3 } + y ^ { 3 } \right) \\ & = 3 x y ( 3 x + y ) \left( 9 x ^ { 2 } - 3 x y + y ^ { 2 } \right) \end{aligned}$

Contestar

$3 x y ( 3 x + y ) \left( 9 x ^ { 2 } - 3 x y + y ^ { 2 } \right)$

Cuando el grado del binomio especial es mayor de dos, es posible que necesitemos aplicar las fórmulas varias veces para obtener una factorización completa. Un polinomio está completamente factorizado ¹⁷ cuando es primo o está escrito como un producto de polinomios primos.

Ejemplo$\PageIndex{12}$

Factorizar completamente$x ^ { 4 } - 81 y ^ { 4 }$.

Solución

En primer lugar, identificar lo que se está cuadrando.

$x ^ { 4 } - 81 y ^ { 4 } = (\:\: ) ^ { 2 } - (\:\: ) ^ { 2 }$

Para ello, recordemos la regla de poder para los exponentes,$(x^{m})^{n}=x^{mn}$. Cuando los exponentes se elevan a una potencia, multiplicarlos. Con esto en mente, encontramos

$x ^ { 4 } - 81 y ^ { 4 } = \left( \color{Cerulean}{x ^ { 2} } \right) ^ { 2 } - \left(\color{Cerulean}{ 9 y ^ { 2} } \right) ^ { 2 }$

Por lo tanto,$a=x^{2}$ y$b=9y^{2}$. Sustituir en la fórmula para diferencia de cuadrados.

$x ^ { 4 } - 81 y ^ { 4 } = \left( x ^ { 2 } + 9 y ^ { 2 } \right) \left( x ^ { 2 } - 9 y ^ { 2 } \right)$

En este punto, observe que el factor$(x^{2}−9y^{2})$ es en sí mismo una diferencia de dos cuadrados y por lo tanto se puede factorizar aún más usando$a=x^{2}$ y$b=3y$. El factor$(x^{2}+9y^{2})$ es primo y no se puede factorizar usando números reales.

$\begin{aligned} x ^ { 4 } - 81 y ^ { 4 } & = \left( x ^ { 2 } + 9 y ^ { 2 } \right) \left( x ^ { 2 } - 9 y ^ { 2 } \right) \\ & = \left( x ^ { 2 } + 9 y ^ { 2 } \right) ( x + 3 y ) ( x - 3 y ) \end{aligned}$

Contestar

$\left( x ^ { 2 } + 9 y ^ { 2 } \right) ( x + 3 y ) ( x - 3 y )$

Al factorizar, siempre busque los factores resultantes para factorizar aún más.

Ejemplo$\PageIndex{13}$

Factorizar completamente$64 x ^ { 6 } - y ^ { 6 }$.

Solución

Este binomio es tanto una diferencia de cuadrados como diferencia de cubos.

$\begin{array} { l } { 64 x ^ { 6 } - y ^ { 6 } = \left( \color{Cerulean}{4 x ^ { 2} } \right) ^ { 3 } - \left( \color{Cerulean}{y ^ { 2} } \right) ^ { 3 } \quad\color{Cerulean} { Difference\: of\: cubes } } \\ { 64 x ^ { 6 } - y ^ { 6 } = \left( \color{Cerulean}{8 x ^ { 3} } \right) ^ { 2 } - \left( \color{Cerulean}{y ^ { 3} } \right) ^ { 2 } \quad \color{Cerulean} { Difference\: of\: squares } } \end{array}$

Cuando se enfrenta a un binomio que es una diferencia tanto de cuadrados como de cubos, como esto es, hacer que sea una regla factorizar usando diferencia de cuadrados primero. Por lo tanto,$a=8x^{3}$ y$b=y^{3}$. Sustituir en la fórmula de diferencia de cuadrados.

$64 x ^ { 6 } - y ^ { 6 } = \left( 8 x ^ { 3 } + y ^ { 3 } \right) \left( 8 x ^ { 3 } - y ^ { 3 } \right)$

Los dos factores binomiales resultantes son suma y diferencia de cubos. Cada uno se puede factorizar aún más. Por lo tanto, tenemos

Figura$\PageIndex{8}$

Los factores trinomiales son primos y la expresión está completamente factorizada.

Contestar

$( 2 x + y ) \left( 4 x ^ { 2 } - 2 x y + y ^ { 2 } \right) ( 2 x - y ) \left( 4 x ^ { 2 } + 2 x y + y ^ { 2 } \right)$

Como ejercicio, factorizar el ejemplo anterior como una diferencia de cubos primero y luego comparar los resultados. ¿Por qué crees que hacemos una regla factorizar primero usando diferencia de cuadrados?

Ejercicio$\PageIndex{3}$

Factor:$a ^ { 6 } b ^ { 6 } - 1$

Contestar

$( a b + 1 ) \left( a ^ { 2 } b ^ { 2 } - a b + 1 \right) ( a b - 1 ) \left( a ^ { 2 } b ^ { 2 } + a b + 1 \right)$

www.youtube.com/v/ozzxrfb7apo

Claves para llevar

• El GCF de dos o más monomios es el producto del GCF de los coeficientes y los factores variables comunes con la menor potencia.
• Si los términos de un polinomio tienen un mayor factor común, entonces factorizar ese GCF usando la propiedad distributiva. Dividir cada término del polinomio entre el GCF para determinar los términos del factor restante.
• Algunos polinomios de cuatro términos se pueden factorizar agrupando los dos primeros términos y los dos últimos términos. Factorizar el GCF de cada grupo y luego factorizar el factor binomial común.
• Al factorizar por agrupación, a veces hay que reorganizar los términos para encontrar un factor binomial común. Después de factorizar el GCF, los factores binomiales restantes deben ser los mismos para que la técnica funcione.
• Al factorizar binomios especiales, el primer paso es identificarlo como una suma o diferencia. Una vez que identificamos el binomio, entonces determinamos los valores de$a$$b$ y luego sustituimos en la fórmula apropiada.
• Si un binomio es tanto una diferencia de cuadrados como de cubos, entonces primero factorizarlo como una diferencia de cuadrados.

Ejercicio$\PageIndex{4}$

Determinar el GCF de las expresiones dadas.

1. $9 x ^ { 5 } , 27 x ^ { 2 } , 15 x ^ { 7 }$
2. $20 y ^ { 4 } , 12 y ^ { 7 } , 16 y ^ { 3 }$
3. $50 x ^ { 2 } y ^ { 3 } , 35 x y ^ { 3 } , 10 x ^ { 3 } y ^ { 2 }$
4. $12 x ^ { 7 } y ^ { 2 } , 36 x ^ { 4 } y ^ { 2 } , 18 x ^ { 3 } y$
5. $15 a ^ { 7 } b ^ { 2 } c ^ { 5 } , 75 a ^ { 7 } b ^ { 3 } c , 45 a b ^ { 4 } c ^ { 3 }$
6. $12 a ^ { 6 } b ^ { 3 } c ^ { 2 } , 48 a b c ^ { 3 } , 125 a ^ { 2 } b ^ { 3 } c$
7. $60 x ^ { 2 } ( 2 x - 1 ) ^ { 3 } , 42 x ( 2 x - 1 ) ^ { 3 } , 6 x ^ { 3 } ( 2 x - 1 )$
8. $14 y ^ { 5 } ( y - 8 ) ^ { 2 } , 28 y ^ { 2 } ( y - 8 ) , 35 y ( y - 8 ) ^ { 3 }$
9. $10 a ^ { 2 } b ^ { 3 } ( a + b ) ^ { 5 } , 48 a ^ { 5 } b ^ { 2 } ( a + b ) ^ { 2 } , 26 a b ^ { 5 } ( a + b ) ^ { 3 }$
10. $45 a b ^ { 7 } ( a - b ) ^ { 7 } , 36 a ^ { 2 } b ^ { 2 } ( a - b ) ^ { 3 } , 63 a ^ { 4 } b ^ { 3 } ( a - b ) ^ { 2 }$

Contestar

1. $3x^{2}$

3. $5xy^{2}$

5. $15ab^{2}c$

7. $6x(2x-1)$

9. $2 a b ^ { 2 } ( a + b ) ^ { 2 }$

Ejercicio$\PageIndex{5}$

Determinar el factor faltante.

1. $18 x ^ { 4 } - 6 x ^ { 3 } + 2 x ^ { 2 } = 2 x ^ { 2 } ( \:\:?\:\: )$
2. $6 x ^ { 5 } - 9 x ^ { 3 } - 3 x = 3 x ( \:\:?\:\: )$
3. $- 10 y ^ { 6 } + 6 y ^ { 4 } - 4 y ^ { 2 } = - 2 y ^ { 2 } ( \:\:?\:\: )$
4. $- 27 y ^ { 9 } - 9 y ^ { 6 } + 3 y ^ { 3 } = - 3 y ^ { 3 } ( \:\:?\:\: )$
5. $12 x ^ { 3 } y ^ { 2 } - 8 x ^ { 2 } y ^ { 3 } + 8 x y = 4 x y ( \:\:?\:\: )$
6. $10 x ^ { 4 } y ^ { 3 } - 50 x ^ { 3 } y ^ { 2 } + 15 x ^ { 2 } y ^ { 2 } = 5 x y ( \:\:?\:\: )$
7. $14 a ^ { 4 } b ^ { 5 } - 21 a ^ { 3 } b ^ { 4 } - 7 a ^ { 2 } b ^ { 3 } = 7 a ^ { 2 } b ^ { 3 } ( \:\:?\:\: )$
8. $15 a ^ { 5 } b ^ { 4 } + 9 a ^ { 4 } b ^ { 2 } - 3 a ^ { 2 } b = 3 a ^ { 2 } b (\:\: ?\:\: )$
9. $x ^ { 3 n } + x ^ { 2 n } + x ^ { n } = x ^ { n } ( \:\:?\:\: )$
10. $y ^ { 4 n } + y ^ { 3 n } - y ^ { 2 n } = y ^ { 2 n } ( \:\:?\:\: )$

Contestar

1. $\left( 9 x ^ { 2 } - 3 x + 1 \right)$

3. $\left( 5 y ^ { 4 } - 3 y ^ { 2 } + 2 \right)$

5. $\left( 3 x ^ { 2 } y - 2 x y ^ { 2 } + 2 \right)$

7. $\left( 2 a ^ { 2 } b ^ { 2 } - 3 a b - 1 \right)$

9. $\left( x ^ { 2 n } + x ^ { n } + 1 \right)$

Ejercicio$\PageIndex{6}$

Factorizar el GCF.

1. $12 x ^ { 4 } - 16 x ^ { 3 } + 4 x ^ { 2 }$
2. $15 x ^ { 5 } - 10 x ^ { 4 } - 5 x ^ { 3 }$
3. $20 y ^ { 8 } + 28 y ^ { 6 } + 40 y ^ { 3 }$
4. $18 y ^ { 7 } - 24 y ^ { 5 } - 30 y ^ { 3 }$
5. $2 a ^ { 4 } b ^ { 3 } - 6 a ^ { 3 } b ^ { 2 } + 8 a ^ { 2 } b$
6. $28 a ^ { 3 } b ^ { 3 } - 21 a ^ { 2 } b ^ { 4 } - 14 a b ^ { 5 }$
7. $2 x ^ { 3 } y ^ { 5 } - 4 x ^ { 4 } y ^ { 4 } + x ^ { 2 } y ^ { 3 }$
8. $3 x ^ { 5 } y - 2 x ^ { 4 } y ^ { 2 } + x ^ { 3 } y ^ { 3 }$
9. $5 x ^ { 2 } ( 2 x + 3 ) - 3 ( 2 x + 3 )$
10. $y ^ { 2 } ( y - 1 ) + 9 ( y - 1 )$
11. $9 x ^ { 2 } ( 3 x - 1 ) + ( 3 x - 1 )$
12. $7 y ^ { 2 } ( 5 y + 2 ) - ( 5 y + 2 )$
13. $x ^ { 5 n } - x ^ { 3 n } + x ^ { n }$
14. $y ^ { 6 n } - y ^ { 3 n } - y ^ { 2 n }$

Contestar

1. $4 x ^ { 2 } \left( 3 x ^ { 2 } - 4 x + 1 \right)$

3. $4 y ^ { 3 } \left( 5 y ^ { 5 } + 7 y ^ { 3 } + 10 \right)$

5. $2 a ^ { 2 } b \left( a ^ { 2 } b ^ { 2 } - 3 a b + 4 \right)$

7. $x ^ { 2 } y ^ { 3 } \left( 2 x y ^ { 2 } - 4 x ^ { 2 } y + 1 \right)$

9. $( 2 x + 3 ) \left( 5 x ^ { 2 } - 3 \right)$

11. $( 3 x - 1 ) \left( 9 x ^ { 2 } + 1 \right)$

13. $x ^ { n } \left( x ^ { 4 n } - x ^ { 2 n } + 1 \right)$

Ejercicio$\PageIndex{7}$

Factorizar por agrupación.

1. $2 x ^ { 3 } + 3 x ^ { 2 } + 2 x + 3$
2. $5 x ^ { 3 } + 25 x ^ { 2 } + x + 5$
3. $6 x ^ { 3 } - 3 x ^ { 2 } + 4 x - 2$
4. $3 x ^ { 3 } - 2 x ^ { 2 } - 15 x + 10$
5. $x ^ { 3 } - x ^ { 2 } - 3 x + 3$
6. $6 x ^ { 3 } - 15 x ^ { 2 } - 2 x + 5$
7. $2 x ^ { 3 } + 7 x ^ { 2 } - 10 x - 35$
8. $3 x ^ { 3 } - x ^ { 2 } + 24 x - 8$
9. $14 y ^ { 4 } + 10 y ^ { 3 } - 7 y - 5$
10. $5 y ^ { 4 } + 2 y ^ { 3 } + 20 y + 8$
11. $x ^ { 4 n } + x ^ { 3 n } + 2 x ^ { n } + 2$
12. $x ^ { 5 n } + x ^ { 3 n } + 3 x ^ { 2 n } + 3$
13. $x ^ { 3 } - x ^ { 2 } y + x y ^ { 2 } - y ^ { 3 }$
14. $x ^ { 3 } + x ^ { 2 } y - 2 x y ^ { 2 } - 2 y ^ { 3 }$
15. $3 x ^ { 3 } y ^ { 2 } + 9 x ^ { 2 } y ^ { 3 } - x - 3 y$
16. $2 x ^ { 3 } y ^ { 3 } - x ^ { 2 } y ^ { 3 } + 2 x - y$
17. $a ^ { 2 } b - 4 a b ^ { 2 } - 3 a + 12 b$
18. $a ^ { 2 } b + 3 a b ^ { 2 } + 5 a + 15 b$
19. $a ^ { 4 } + a ^ { 2 } b ^ { 3 } + a ^ { 2 } b + b ^ { 4 }$
20. $a ^ { 3 } b + 2 a ^ { 2 } + 3 a b ^ { 4 } + 6 b ^ { 3 }$
21. $3 a x + 10 b y - 5 a y - 6 b x$
22. $a ^ { 2 } x - 5 b ^ { 2 } y - 5 a ^ { 2 } y + b ^ { 2 } x$
23. $x ^ { 4 } y ^ { 2 } - x ^ { 3 } y ^ { 3 } + x ^ { 2 } y ^ { 4 } - x y ^ { 5 }$
24. $2 x ^ { 5 } y ^ { 2 } + 4 x ^ { 4 } y ^ { 2 } + 18 x ^ { 3 } y + 36 x ^ { 2 } y$
25. $a ^ { 5 } b ^ { 2 } + a ^ { 4 } b ^ { 4 } + a ^ { 3 } b ^ { 3 } + a ^ { 2 } b ^ { 5 }$
26. $3 a ^ { 6 } b + 3 a ^ { 5 } b ^ { 2 } + 9 a ^ { 4 } b ^ { 2 } + 9 a ^ { 3 } b ^ { 3 }$

Contestar

1. $( 2 x + 3 ) \left( x ^ { 2 } + 1 \right)$

3. $( 2 x - 1 ) \left( 3 x ^ { 2 } + 2 \right)$

5. $( x - 1 ) \left( x ^ { 2 } - 3 \right)$

7. $( 2 x + 7 ) \left( x ^ { 2 } - 5 \right)$

9. $( 7 y + 5 ) \left( 2 y ^ { 3 } - 1 \right)$

11. $\left( x ^ { n } + 1 \right) \left( x ^ { 3 n } + 2 \right)$

13. $( x - y ) \left( x ^ { 2 } + y ^ { 2 } \right)$

15. $( x + 3 y ) \left( 3 x ^ { 2 } y ^ { 2 } - 1 \right)$

17. $( a - 4 b ) ( a b - 3 )$

19. $\left( a ^ { 2 } + b \right) \left( a ^ { 2 } + b ^ { 3 } \right)$

21. $( a - 2 b ) ( 3 x - 5 y )$

23. $x y ^ { 2 } ( x - y ) \left( x ^ { 2 } + y ^ { 2 } \right)$

25. $a ^ { 2 } b ^ { 2 } \left( a ^ { 2 } + b \right) \left( a + b ^ { 2 } \right)$

Ejercicio$\PageIndex{8}$

Factor.

1. $x^{2}-64$
2. $x^{2}-100$
3. $9-4y^{2}$
4. $25 - y^{2}$
5. $x ^ { 2 } - 81 y ^ { 2 }$
6. $x ^ { 2 } - 49 y ^ { 2 }$
7. $a ^ { 2 } b ^ { 2 } - 4$
8. $1 - 9 a ^ { 2 } b ^ { 2 }$
9. $a ^ { 2 } b ^ { 2 } - c ^ { 2 }$
10. $4 a ^ { 2 } - b ^ { 2 } c ^ { 2 }$
11. $x ^ { 4 } - 64$
12. $36 - y ^ { 4 }$
13. $( 2 x + 5 ) ^ { 2 } - x ^ { 2 }$
14. $( 3 x - 5 ) ^ { 2 } - x ^ { 2 }$
15. $y ^ { 2 } - ( y - 3 ) ^ { 2 }$
16. $y ^ { 2 } - ( 2 y + 1 ) ^ { 2 }$
17. $( 2 x + 5 ) ^ { 2 } - ( x - 3 ) ^ { 2 }$
18. $( 3 x - 1 ) ^ { 2 } - ( 2 x - 3 ) ^ { 2 }$
19. $x ^ { 4 } - 16$
20. $81 x ^ { 4 } - 1$
21. $x ^ { 4 } y ^ { 4 } - 1$
22. $x ^ { 4 } - y ^ { 4 }$
23. $x ^ { 8 } - y ^ { 8 }$
24. $y ^ { 8 } - 1$
25. $x ^ { 2 n } - y ^ { 2 n }$
26. $x ^ { 2 n } y ^ { 2 n } - 4$
27. $x ^ { 4 n } - y ^ { 4 n }$
28. $x ^ { 4 n } y ^ { 4 n } - 16$
29. $x ^ { 3 } - 27$
30. $8 x ^ { 3 } - 125$
31. $8 y ^ { 3 } + 27$
32. $64 x ^ { 3 } + 343$
33. $x ^ { 3 } - y ^ { 3 }$
34. $x ^ { 3 } + y ^ { 3 }$
35. $8 a ^ { 3 } b ^ { 3 } + 1$
36. $27 a ^ { 3 } - 8 b ^ { 3 }$
37. $x ^ { 3 } y ^ { 3 } - 125$
38. $216 x ^ { 3 } + y ^ { 3 }$
39. $x ^ { 3 } + ( x + 3 ) ^ { 3 }$
40. $y ^ { 3 } - ( 2 y - 1 ) ^ { 3 }$
41. $( 2 x + 1 ) ^ { 3 } - x ^ { 3 }$
42. $( 3 y - 5 ) ^ { 3 } - y ^ { 3 }$
43. $x ^ { 3 n } - y ^ { 3 n }$
44. $x ^ { 3 n } + y ^ { 3 n }$
45. $a ^ { 6 } + 64$
46. $64 a ^ { 6 } - 1$
47. $x ^ { 6 } - y ^ { 6 }$
48. $x ^ { 6 } + y ^ { 6 }$
49. $x ^ { 6 n } - y ^ { 6 n }$
50. $x ^ { 6 n } + y ^ { 6 n }$
51. Dado$f (x) = 2x − 1$, demuéstralo$(f + f ) (x) = 2f (x)$.
52. Dado$f (x) = x^{2} − 3x + 2$, demuéstralo$(f + f ) (x) = 2f (x)$.
53. Dado$f (x) = mx + b$, demuéstralo$(f + f ) (x) = 2f (x)$.
54. Dado$f (x) = ax^{2} + bx + c$, demuéstralo$(f + f ) (x) = 2f (x)$.
55. Dado$f (x) = ax^{2} + bx + c$, demuéstralo$(f − f ) (x) = 0$.
56. Dado$f (x) = mx + b$, demuéstralo$(f − f ) (x) = 0$.

Contestar

1. $( x + 8 ) ( x - 8 )$

3. $( 3 + 2 y ) ( 3 - 2 y )$

5. $( x + 9 y ) ( x - 9 y )$

7. $( a b + 2 ) ( a b - 2 )$

9. $( a b + c ) ( a b - c )$

11. $\left( x ^ { 2 } + 8 \right) \left( x ^ { 2 } - 8 \right)$

13. $( 3 x + 5 ) ( x + 5 )$

15. $3 ( 2 y - 3 )$

17. $( 3 x + 2 ) ( x + 8 )$

19. $\left( x ^ { 2 } + 4 \right) ( x + 2 ) ( x - 2 )$

21. $\left( x ^ { 2 } y ^ { 2 } + 1 \right) ( x y + 1 ) ( x y - 1 )$

23. $\left( x ^ { 4 } + y ^ { 4 } \right) \left( x ^ { 2 } + y ^ { 2 } \right) ( x + y ) ( x - y )$

25. $\left( x ^ { n } + y ^ { n } \right) \left( x ^ { n } - y ^ { n } \right)$

27. $\left( x ^ { 2 n } + y ^ { 2 n } \right) \left( x ^ { n } + y ^ { n } \right) \left( x ^ { n } - y ^ { n } \right)$

29. $( x - 3 ) \left( x ^ { 2 } + 3 x + 9 \right)$

31. $( 2 y + 3 ) \left( 4 y ^ { 2 } - 6 y + 9 \right)$

33. $( x - y ) \left( x ^ { 2 } + x y + y ^ { 2 } \right)$

35. $( 2 a b + 1 ) \left( 4 a ^ { 2 } b ^ { 2 } - 2 a b + 1 \right)$

37. $( x y - 5 ) \left( x ^ { 2 } y ^ { 2 } + 5 x y + 25 \right)$

39. $( 2 x + 3 ) \left( x ^ { 2 } + 3 x + 9 \right)$

41. $( x + 1 ) \left( 7 x ^ { 2 } + 5 x + 1 \right)$

43. $\left( x ^ { n } - y ^ { n } \right) \left( x ^ { 2 n } + x ^ { n } y ^ { n } + y ^ { 2 n } \right)$

45. $\left( a ^ { 2 } + 4 \right) \left( a ^ { 4 } - 4 a ^ { 2 } + 16 \right)$

47. $( x + y ) \left( x ^ { 2 } - x y + y ^ { 2 } \right) ( x - y ) \left( x ^ { 2 } + x y + y ^ { 2 } \right)$

49. $\begin{array} { l } { \left( x ^ { n } + y ^ { n } \right) \left( x ^ { 2 n } - x ^ { n } y ^ { n } + y ^ { 2 n } \right) } { \times \left( x ^ { n } - y ^ { n } \right) \left( x ^ { 2 n } + x ^ { n } y ^ { n } + y ^ { 2 n } \right) } \end{array}$

51. La respuesta puede variar

53. La respuesta puede variar

55. La respuesta puede variar

Ejercicio$\PageIndex{9}$

1. ¿Qué se puede decir sobre el grado de un factor de un polinomio? Dé un ejemplo.
2. Si un binomio cae en ambas categorías, diferencia de cuadrados y diferencia de cubos, cuál sería mejor usar para factorizar, y ¿por qué? Crear un ejemplo que ilustre esta situación y factorizarla usando ambas fórmulas.
3. Escribe tus propios ejemplos para cada uno de los tres tipos especiales de binomio. Factorializarlos y compartir sus resultados.

Contestar

1. La respuesta puede variar

3. La respuesta puede variar

Notas al pie

⁵ El proceso de escribir un número o expresión como producto.

⁶ Cualquier combinación de factores, multiplicados entre sí, dando como resultado el producto.

⁷ Cualquiera de los números o expresiones que forman un producto.

⁸ El producto de los factores variables comunes y el GCF de los coeficientes.

⁹ Expresiones que no comparten otros factores comunes que no sean$1$.

¹⁰ El proceso de reescribir un polinomio como producto utilizando el GCF de todos sus términos.

¹¹ Un polinomio con coeficientes enteros que no pueden ser factorizados como un producto de polinomios con coeficientes enteros distintos de$1$ y en sí mismo.

¹² Técnica para factorizar polinomios con cuatro términos.

¹³$a ^ { 2 } - b ^ { 2 } = ( a + b ) ( a - b )$, donde$a$ y$b$ representan expresiones algebraicas.

¹⁴$a^{2} + b^{2}$, donde$a$ y$b$ representan expresiones algebraicas. Esto no tiene un equivalente factorizado general.

¹⁵$a^{3} + b^{3} = (a+b)(a^{2} - ab + b^{2})$ donde$a$ y$b$ representan expresiones algebraicas.

¹⁶$a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})$ donde$a$ y$b$ representan expresiones algebraicas.

¹⁷ Un polinomio que es primo o escrito como producto de polinomios primos.