4.3: Factorización de Trinomios

Objetivos de aprendizaje

• Trinomios factoriales de la forma\(x^{2}+bx+c\).
• Trinomios factoriales de grado superior.
• Trinomios factoriales de la forma\(ax^{2}+bx+c\).
• Trinomios factoriales utilizando el método AC.

Factorización de trinomios cuyo coeficiente principal es uno

(Factorización de Trinomios de la Forma\(x^{2}+bx+c\))

Algunos trinomios de la forma\(x^{2}+bx+c\) pueden ser factorizados como producto de binomios. Si un trinomio de este tipo factores, entonces tenemos:

\(\begin{aligned} x ^ { 2 } + b x + c & = ( x + m ) ( x + n ) \\ & = x ^ { 2 } + n x + m x + m n \\ & = x ^ { 2 } + ( n + m ) x + m n \end{aligned}\)

Esto nos da

\(b=n+m\)y\(c=mn\)

En definitiva, si lo es el coeficiente principal de un trinomio factoriable\(1\), entonces los factores del último término deben sumar al coeficiente del término medio. Esta observación es la clave para factorizar trinomios utilizando la técnica conocida como método de ensayo y error (o adivinar y verificar) ¹⁸.

Ejemplo\(\PageIndex{1}\):

Factor\(x^{2}+12x+20\).

Solución

Comenzamos por escribir dos juegos de paréntesis en blanco. Si un trinomio de esta forma factores, entonces se factorizará en dos factores binomiales lineales.

\(x ^ { 2 } + 12 x + 20 = ( \quad ) ( \quad)\)

Escribe los factores del primer término en el primer espacio de cada conjunto de paréntesis. En este caso, factor\(x^{2}=x⋅x\).

\(x ^ { 2 } + 12 x + 20 = ( x \quad ) ( x\quad )\)

Determinar los factores del último término cuya suma sea igual al coeficiente del término medio. Para ello, enumere todas las factorizaciones de\(20\) y busque factores cuya suma sea igual\(12\).

\(\begin{aligned} 20 & = 1 \cdot 20 \:\:\rightarrow\:\: 1 + 20 = 21 \\ & =\color{OliveGreen}{ 2 \cdot 10 \:\:\rightarrow\:\: 2 + 10}\color{black}{ =}\color{OliveGreen}{ 12} \\ & = 4 \cdot 5 \:\:\:\:\rightarrow\:\: 4 + 5 = 9 \end{aligned}\)

Elige\(20 = 2 ⋅ 10\) porque\(2 + 10 = 12\). Escribir en el último término de cada binomio utilizando los factores determinados en el paso anterior.

\(x ^ { 2 } + 12 x + 20 = ( x + 2 ) ( x + 10 )\)

Esto se puede interpretar visualmente de la siguiente manera:

Figura\(\PageIndex{1}\)

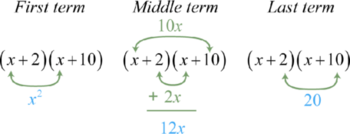
Verificar multiplicando los dos binomios.

\(\begin{aligned} ( x + 2 ) ( x + 10 ) & = x ^ { 2 } + 10 x + 2 x + 20 \\ & = x ^ { 2 } + 12 x + 20 \:\:\color{Cerulean}{✓} \end{aligned}\)

Contestar

\[(x+2)(x+10) \nonumber\]

Dado que la multiplicación es conmutativa, el orden de los factores no importa.

\(\begin{aligned} x ^ { 2 } + 12 x + 20 & = ( x + 2 ) ( x + 10 ) \\ & = ( x + 10 ) ( x + 2 ) \end{aligned}\)

Si el último término del trinomio es positivo, entonces ambos factores constantes deben ser negativos o ambos deben ser positivos.

Ejemplo\(\PageIndex{2}\):

Factor\(x ^ { 2 } y ^ { 2 } - 7 x y + 12\).

Solución

Primero, factor\(x^{2}y^{2}=xy⋅xy\).

\(x ^ { 2 } y ^ { 2 } - 7 x y + 12 = ( x y \quad \color{Cerulean}{?}\color{black}{ )} ( x y \quad\color{Cerulean}{?}\color{black}{ )}\)

A continuación, buscar factores de\(12\) cuya suma es\(−7\).

\(\begin{aligned} 12 & = 1 \cdot 12 \:\:\rightarrow\:\: - 1 + ( - 12 ) = - 13 \\ & = 2 \cdot 6 \:\:\:\:\rightarrow\:\: - 2 + ( - 6 ) = - 8 \\ & = \color{OliveGreen}{3 \cdot 4\:\:\:\: \rightarrow\:\: - 3 + ( - 4 ) = - 7} \end{aligned}\)

En este caso, elige\(−3\) y\(−4\) porque\((−3)(−4)=+12\) y\(−3+(−4)=−7\).

\(\begin{aligned} x ^ { 2 } y ^ { 2 } - 7 x y + 12 & = ( x y\quad \color{Cerulean}{?}\color{black}{ )} ( x y\quad\color{Cerulean}{ ?}\color{black}{ )} \\ & = ( x y - 3 ) ( x y - 4 ) \end{aligned}\)

Cheque

\(\begin{aligned} ( x y - 3 ) ( x y - 4 ) & = x ^ { 2 } y ^ { 2 } - 4 x y - 3 x y + 12 \\ & = x ^ { 2 } y ^ { 2 } - 7 x y + 12 \:\:\color{Cerulean}{✓} \end{aligned}\)

Contestar

\(( x y - 3 ) ( x y - 4 )\)

Si el último término del trinomio es negativo, entonces uno de sus factores debe ser negativo.

Ejemplo\(\PageIndex{3}\):

Factor:\(x ^ { 2 } - 4 x y - 12 y ^ { 2 }\).

Solución

Comience por factorizar el primer término\(x ^ { 2 } = x \cdot x\).

\(x ^ { 2 } - 4 x y - 12 y ^ { 2 } = \left( \begin{array} { l l } { x } & { \color{Cerulean}{?} } \end{array} \right) \left( \begin{array} { l l } { x } & { \color{Cerulean}{?} } \end{array} \right)\)

Los factores de\(12\) se enumeran a continuación. En este ejemplo, estamos buscando factores cuya suma sea\(−4\).

\(\begin{aligned} 12 & = 1 \cdot 12 \:\:\rightarrow\:\: 1 + ( - 12 ) = - 11 \\ & =\color{OliveGreen}{ 2 \cdot 6\:\:\:\: \rightarrow\:\: 2 + ( - 6 ) = - 4} \\ & = 3 \cdot 4\:\:\:\: \rightarrow\:\: 3 + ( - 4 ) = - 1 \end{aligned}\)

Por lo tanto, el coeficiente del último término se puede factorizar como\(−12=2(−6)\), dónde\(2+(−6)=−4\). Porque el último término tiene un factor variable de\(y^{2}\), usa\(−12y^{2}=2y(−6y)\) y factoriza el trinomio de la siguiente manera:

\(\begin{aligned} x ^ { 2 } - 4 x y - 12 y ^ { 2 } & = ( x \quad \color{Cerulean}{?}\color{black}{ )} ( x \quad \color{Cerulean}{?}\color{black}{ )} \\ & = ( x + 2 y ) ( x - 6 y ) \end{aligned}\)

Multiplicar para verificar.

\(\begin{aligned} ( x + 2 y ) ( x - 6 y ) & = x ^ { 2 } - 6 x y + 2 y x - 12 y ^ { 2 } \\ & = x ^ { 2 } - 6 x y + 2 x y - 12 y ^ { 2 } \\ & = x ^ { 2 } - 4 x y - 12 y ^ { 2 } \:\:\color{Cerulean}{✓}\end{aligned}\)

Contestar

\(( x + 2 y ) ( x - 6 y )\)

A menudo nuestra primera conjetura no producirá una factorización correcta. Este proceso puede requerir ensayos repetidos. Por esta razón, el cheque es muy importante y no es opcional.

Ejemplo\(\PageIndex{4}\):

Factor\(a ^ { 2 } + 10 a - 24\).

Solución

El primer término de este trinomio,\(a^{2}\), factores como\(a⋅a\).

\(a ^ { 2 } + 10 a - 24 = \left( \begin{array} { l l } { a } & { ? } \end{array} \right) \left( \begin{array} { l l } { a } & { ? } \end{array} \right)\)

Considere los factores de\(24\):

\(\begin{aligned} 24 & = 1 \cdot 24 \\ & = \color{OliveGreen}{2 \cdot 12} \\ & = 3 \cdot 8 \\ & = \color{red}{4 \cdot 6} \end{aligned}\)

Supongamos que elegimos los factores\(4\) y\(6\) porque\(4 + 6 = 10\), el coeficiente del término medio. Entonces tenemos la siguiente factorización incorrecta:

\(a ^ { 2 } + 10 a - 24 \stackrel{\color{red}{?}}{\color{black}{=}} ( a + 4 ) ( a + 6 ) \:\:\color{red}{Incorrect\:Factorization}\)

Cuando multiplicamos para verificar, encontramos el error.

\(\begin{aligned} ( a + 4 ) ( a + 6 ) & = a ^ { 2 } + 6 a + 4 a + 24 \\ & = a ^ { 2 } + 10 a \color{red}{+ 24}\:\:\color{red}{✗} \end{aligned}\)

En este caso, el término medio es correcto pero el último término no lo es. Dado que el último término en la expresión original es negativo, necesitamos elegir factores que sean de signo opuesto. Por lo tanto, debemos volver a intentarlo. Esta vez elegimos los factores\(−2\) y\(12\) porque\(−2+12=10\).

\(a ^ { 2 } + 10 a - 24 = ( a - 2 ) ( a + 12 )\)

Ahora la comprobación muestra que esta factorización es correcta.

\(\begin{aligned} ( a - 2 ) ( a + 12 ) & = a ^ { 2 } + 12 a - 2 a - 24 \\ & = a ^ { 2 } + 10 a \color{OliveGreen}{- 24}\:\:\color{Cerulean}{✓} \end{aligned}\)

Contestar

\(( a - 2 ) ( a + 12 )\)

Si elegimos los factores sabiamente, entonces podemos reducir gran parte de las conjeturas en este proceso. No obstante, si una conjetura no es correcta, no te desanimes; solo prueba un conjunto diferente de factores. Ten en cuenta que algunos polinomios son primos. Por ejemplo, consideremos el trinomio\(x^{2}+3x+20\) y los factores de\(20\):

\(\begin{aligned} 20 & = 1 \cdot 20 \\ & = 2 \cdot 10 \\ & = 4 \cdot 5 \end{aligned}\)

No hay factores de\(20\) cuya suma sea\(3\). Por lo tanto, el trinomio original no puede ser factorizado como producto de dos binomios con coeficientes enteros. El trinomio es primo.

Factorización de Trinomios de Grado Superior

Podemos utilizar la técnica de ensayo y error para factorizar trinomios de grado superior.

Ejemplo\(\PageIndex{5}\):

Factor\(x ^ { 4 } + 6 x ^ { 2 } + 5\).

Solución

Comience por factorizar el primer término\(x ^ { 4 } = x ^ { 2 } \cdot x ^ { 2 }\).

\(x ^ { 4 } + 6 x ^ { 2 } + 5 = \left( x ^ { 2 } \quad \color{Cerulean}{?} \right) \left( x ^ { 2 } \quad \color{Cerulean}{?} \right)\)

Ya que\(5\) es primo y el coeficiente del término medio es positivo, elegir\(+1\) y\(+5\) como los factores del último término.

\(\begin{aligned} x ^ { 4 } + 6 x ^ { 2 } + 5 & = \left( x ^ { 2 } \quad \color{Cerulean}{?} \right) \left( x ^ { 2 } \quad \color{Cerulean}{?} \right) \\ & = \left( x ^ { 2 } + 1 \right) \left( x ^ { 2 } + 5 \right) \end{aligned}\)

Observe que la parte variable del término medio es\(x^{2}\) y la factorización echa un vistazo.

\(\begin{aligned} \left( x ^ { 2 } + 1 \right) \left( x ^ { 2 } + 5 \right) & = x ^ { 4 } + 5 x ^ { 2 } + x ^ { 2 } + 5 \\ & = x ^ { 4 } + 6 x ^ { 2 } + 5\:\:\color{Cerulean}{✓} \end{aligned}\)

Contestar

\(\left( x ^ { 2 } + 1 \right) \left( x ^ { 2 } + 5 \right)\)

Ejemplo\(\PageIndex{6}\):

Factor:\(x ^ { 2 n } + 4 x ^ { n } - 21\) donde\(n\) es un entero positivo.

Solución

Comience por factorizar el primer término\(x ^ { 2 n } = x ^ { n } \cdot x ^ { n }\).

\(x ^ { 2 n } + 4 x ^ { n } - 21 = \left( \begin{array} { l l } { x ^ { n } } & { \color{Cerulean}{?} } \end{array} \right) \left( \begin{array} { l l } { x ^ { n } } & {\color{Cerulean}{ ?} } \end{array} \right)\)

Factorizar\(- 21 = 7 ( - 3 )\) porque\(7 + ( - 3 ) = + 4\) y escribir

\(\begin{aligned} x ^ { 2 n } + 4 x ^ { n } - 21 & = \left( x ^ { n } \quad \color{Cerulean}{?} \right) \left( x ^ { n } \quad \color{Cerulean}{?} \right) \\ & = \left( x ^ { n } + 7 \right) \left( x ^ { n } - 3 \right) \end{aligned}\)

Contestar

\[\left( x ^ { n } + 7 \right) \left( x ^ { n } - 3 \right) \nonumber\]

El cheque se deja al lector.

Ejercicio\(\PageIndex{1}\)

Factor\(x ^ { 6 } - x ^ { 3 } - 42\).

Contestar

\[\left( x ^ { 3 } + 6 \right) \left( x ^ { 3 } - 7 \right) \nonumber\]

Factorización de trinomios cuyo coeficiente principal no es uno

(Factorización de Trinomios de la Forma\(ax^{2}+bx+c\))

Factorizar trinomios de la forma\(ax^{2}+bx+c\) puede ser un desafío porque el término medio se ve afectado por los factores de ambos\(a\) y\(c\). En general,

\(\begin{aligned} \color{Cerulean}{a}\color{black}{ x} ^ { 2 } + \color{Cerulean}{b}\color{black}{ x} + \color{Cerulean}{c} & = ( p x + m ) ( q x + n ) \\ & = p q x ^ { 2 } + p n x + q m x + m n \\ & = \color{Cerulean}{p q}\color{black}{ x} ^ { 2 } + \color{Cerulean}{( p n + q m ) }\color{black}{x} + \color{Cerulean}{m n} \end{aligned}\)

Esto nos da,

\(a=pq\)y\(b=pn+qm\), donde\(c=mn\)

En definitiva, cuando el coeficiente principal de un trinomio es algo distinto a\(1\), habrá más a considerar a la hora de determinar los factores utilizando el método de ensayo y error. La clave radica en la comprensión de cómo se obtiene el término medio. Multiplicar\((5x+3)(2x+3)\) y seguir cuidadosamente la formación del término medio.

Figura\(\PageIndex{2}\)

Como hemos visto antes, el producto de los primeros términos de cada binomio es igual al primer término del trinomio. El término medio del trinomio es la suma de los productos de los términos externo e interno de los binomios. El producto de los últimos términos de cada binomio es igual al último término del trinomio. Visualmente, tenemos lo siguiente:

Figura\(\PageIndex{3}\)

Por ello, necesitamos buscar productos de los factores del primer y último término cuya suma sea igual al coeficiente del término medio. Por ejemplo, para factorizar\(6x^{2}+29x+35\), mirar los factores de\(6\) y\(35\).

\(\begin{aligned} 6 & = 1 \cdot 635 = 1 \cdot 35 \\ & = \color{OliveGreen}{2 \cdot 3} \quad \color{black}{=}\color{OliveGreen}{ 5 \cdot 7} \end{aligned}\)

La combinación que produce el coeficiente del término medio es\(2⋅7+3⋅5=14+15=29\). Asegúrese de que los términos externos tengan coeficientes\(2\) y\(7\), y que los términos internos tengan coeficientes\(5\) y\(3\). Utilice esta información para factorizar el trinomio.

\(\begin{aligned} 6 x ^ { 2 } + 29 x + 35 & = ( 2 x \quad \color{Cerulean}{?}\color{black}{ )} ( 3 x \quad \color{Cerulean}{?}\color{black}{ )} \\ & = ( 2 x + 5 ) ( 3 x + 7 ) \end{aligned}\)

Siempre podemos verificar multiplicando; esto se deja al lector.

Ejemplo\(\PageIndex{7}\)

Factor\(5 x ^ { 2 } + 16 x y + 3 y ^ { 2 }\).

Solución

Dado que el coeficiente principal y el último término son ambos primos, solo hay una manera de factorizar cada uno.

\(5=1⋅5\)y\(3=1⋅3\)

Comience por escribir los factores del primer término,\(5x^{2}\), de la siguiente manera:

\(5 x ^ { 2 } + 16 x y + 3 y ^ { 2 } = ( x \quad \color{Cerulean}{?} \color{black}{)} ( 5 x \quad \color{Cerulean}{?}\color{black}{ )}\)

El término medio y último son ambos positivos; por lo tanto, los factores de\(3\) se eligen como números positivos. En este caso, la única opción es en qué agrupación colocar estos factores.

\((x+y)(5x+3y)\)o\((x+3y)(5x+y)\)

Determine qué agrupación es correcta multiplicando cada expresión.

\(\begin{aligned} ( x + y ) ( 5 x + 3 y ) & = 5 x ^ { 2 } + 3 x y + 5 x y + 3 y ^ { 2 } \\ & = 5 x ^ { 2 } + 8 x y + 3 y ^ { 2 } x \:\:\color{red}{✗} \\ ( x + 3 y ) ( 5 x + y ) & = 5 x ^ { 2 } + x y + 15 x y + 3 y ^ { 2 } \\ & = 5 x ^ { 2 } + 16 x y + 3 y ^ { 2 } \:\:\color{Cerulean}{✓}\end{aligned}\)

Contestar

\(( x + 3 y ) ( 5 x + y )\)

Ejemplo\(\PageIndex{8}\)

Factor:\(18 a ^ { 2 } b ^ { 2 } - a b - 4\).

Solución

Primero, considere los factores de los coeficientes del primer y último término.

\(\begin{aligned} 18 & = 1 \cdot 18\:\quad4 =\color{OliveGreen}{ 1 \cdot 4} \\ & =\color{OliveGreen}{ 2 \cdot 9} \:\:\:\:\:\quad\color{black}{=} 2 \cdot 2 \\ & = 3 \cdot 6 \end{aligned}\)

Estamos buscando productos de factores cuya suma sea igual al coeficiente del término medio,\(−1\). Después de pensarlo, podemos ver que la suma de\(8\) y\(−9\) es\(−1\) y la combinación que da esto sigue:

\(2 ( 4 ) + 9 ( - 1 ) = 8 - 9 = - 1\)

La factorización comienza en este punto con dos conjuntos de paréntesis en blanco.

\(18 a ^ { 2 } b ^ { 2 } - a b - 4 = ( \quad ) (\quad )\)

Uso\(2ab\) y\(9ab\) como factores de\(18a^{2}b^{2}\).

\(18 a ^ { 2 } b ^ { 2 } - a b - 4 = ( 2 a b \quad \color{Cerulean}{?}\color{black}{ )} \:( 9 a b\quad\color{Cerulean}{ ?}\color{black}{ )}\)

A continuación utilice los factores\(1\) y\(4\) en el orden correcto para que los productos internos y externos sean\(−9ab\) y\(8ab\) respectivamente.

\(18 a ^ { 2 } b ^ { 2 } - a b - 4 = ( 2 a b - 1 ) ( 9 a b + 4 )\)

Contestar

\(( 2 a b - 1 ) ( 9 a b + 4 )\). La comprobación completa se deja al lector.

Es una buena práctica factorizar primero el GCF, si lo hay. Hacer esto produce un factor trinomial con coeficientes más pequeños. Como hemos visto, los trinomios con coeficientes menores requieren mucho menos esfuerzo para factorizar. Este paso que comúnmente se pasa por alto merece la pena identificarlo temprano.

Ejemplo\(\PageIndex{9}\):

Factor\(12 y ^ { 3 } - 26 y ^ { 2 } - 10 y\).

Solución

Comience por factorizar el GCF.

\(12 y ^ { 3 } - 26 y ^ { 2 } - 10 y = 2 y \left( 6 y ^ { 2 } - 13 y - 5 \right)\)

Después de factorizar\(2y\), los coeficientes del trinomio resultante son menores y tienen menos factores. Podemos factorizar el trinomio resultante usando\(6=2(3)\) y\(5=(5)(1)\). Observe que estos factores pueden producir\(−13\) de dos maneras:

\(\begin{array} { l } { 2 ( - 5 ) + 3 ( - 1 ) = - 10 - 3 = - 13 } \\ { 2 ( \color{OliveGreen}{1}\color{black}{ )} + 3 (\color{OliveGreen}{ - 5}\color{black}{ )} = 2 - 15 = - 13 } \end{array}\)

Porque el último término es\(−5\), la combinación correcta requiere de los factores\(1\) y\(5\) ser signos opuestos. Aquí usamos\(2(1) = 2\) y\(3(−5) = −15\) porque la suma es\(−13\) y el producto de\((1)(−5) = −5\).

\(\begin{aligned} 12 y ^ { 3 } - 26 y ^ { 2 } - 10 y & = 2 y \left( 6 y ^ { 2 } - 13 y - 5 \right) \\ & = 2 y ( 2 y\quad \color{Cerulean}{?}\color{black}{ )} ( 3 y\quad\color{Cerulean}{ ?}\color{black}{ )} \\ & = 2 y ( 2 y - 5 ) ( 3 y + 1 ) \end{aligned}\)

Cheque.

\(\begin{aligned} 2 y ( 2 y - 5 ) ( 3 y + 1 ) & = 2 y \left( 6 y ^ { 2 } + 2 y - 15 y - 5 \right) \\ & = 2 y \left( 6 y ^ { 2 } - 13 y - 5 \right) \\ & = 12 y ^ { 3 } - 26 y ^ { 2 } - 10 y\color{Cerulean}{✓} \end{aligned}\)

El factor\(2y\) es parte de la forma factorizada de la expresión original; asegúrese de incluirla en la respuesta.

Contestar

\(2 y ( 2 y - 5 ) ( 3 y + 1 )\)

Es una buena práctica trabajar consistentemente con trinomios donde el coeficiente principal es positivo. Si el coeficiente principal es negativo, factorializarlo junto con cualquier GCF. Tenga en cuenta que a veces el factor será\(−1\).

Ejemplo\(\PageIndex{10}\)

Factor:\(- 18 x ^ { 6 } - 69 x ^ { 4 } + 12 x ^ { 2 }\).

Solución

En este ejemplo, el GCF es\(3x^{2}\). Debido a que el coeficiente principal es negativo comenzamos por factorizar\(−3x^{2}\).

\(- 18 x ^ { 6 } - 69 x ^ { 4 } + 12 x ^ { 2 } = - 3 x ^ { 2 } \left( 6 x ^ { 4 } + 23 x ^ { 2 } - 4 \right)\)

En este punto, factorizar el trinomio restante como de costumbre, recordando escribir el\(−3x^{2}\) como factor en la respuesta final. Uso\(6 = 1(6)\) y\(−4 = 4(−1) \) porque\(1(−1)+6(4)=23\). Por lo tanto,

\(\begin{aligned} - 18 x ^ { 6 } - 69 x ^ { 4 } + 12 x ^ { 2 } & = - 3 x ^ { 2 } \left( 6 x ^ { 4 } + 23 x ^ { 2 } - 4 \right) \\ & = - 3 x ^ { 2 } \left( x ^ { 2\quad } \right) \left( 6 x ^ { 2 }\quad \right) \\ & = - 3 x ^ { 2 } \left( x ^ { 2 } + 4 \right) \left( 6 x ^ { 2 } - 1 \right) \end{aligned}\)

Contestar

\(- 3 x ^ { 2 } \left( x ^ { 2 } + 4 \right) \left( 6 x ^ { 2 } - 1 \right)\). El cheque se deja al lector.

Ejercicio\(\PageIndex{2}\)

Factor:\(- 12 a ^ { 5 } b + a ^ { 3 } b ^ { 3 } + a b ^ { 5 }\).

Contestar

\(- a b \left( 3 a ^ { 2 } - b ^ { 2 } \right) \left( 4 a ^ { 2 } + b ^ { 2 } \right)\)

www.youtube.com/v/Aigcuutobk4

Factorización mediante el método de CA

Una técnica alternativa para factorizar trinomios, llamada método AC ¹⁹, hace uso del método de agrupación para factorizar polinomios de cuatro términos. Si un trinomio en la forma\(ax^{2}+bx+c\) puede ser factorizado, entonces el término medio,\(bx\), puede ser reemplazado por dos términos con coeficientes cuya suma es\(b\) y producto es\(ac\). Esta sustitución da como resultado una expresión equivalente con cuatro términos que se pueden factorizar por agrupación.

Ejemplo\(\PageIndex{11}\):

Factor usando el método AC:\(18 x ^ { 2 } - 31 x + 6\).

Solución

Aquí\(a=18, b=-31\), y\(c=6\).

\(\begin{aligned} a c & = 18 ( 6 ) \\ & = 108 \end{aligned}\)

Factor\(108\), y buscar factores cuya suma sea\(−31\).

\ begin {alineado} 108 & = - 1 (- 108)\\ & = - 2 (- 54)\\ & = - 3 (- 36)\\ & =\ color {OliveGreen} {- 4 (- 27)}\ color {cerúleo} {✓}\\ &\ color {negro} {=} - 6 (- 18)\\ & = - 9 (- 12)\ final {alineado}

En este caso, la suma de los factores\(−27\) y\(−4\) es igual al coeficiente medio,\(−31\). Por lo tanto\(−31x=−27x−4x\),, y podemos escribir

\(18 x ^ { 2 } \color{OliveGreen}{- 31 x}\color{black}{ +} 6 = 18 x ^ { 2 } \color{OliveGreen}{- 27 x - 4 x}\color{black}{ +} 6\)

Factorizar la expresión equivalente por agrupación.

\(\begin{aligned} 18 x ^ { 2 } - 31 x + 6 & = 18 x ^ { 2 } - 27 x - 4 x + 6 \\ & = 9 x ( 2 x - 3 ) - 2 ( 2 x - 3 ) \\ & = ( 2 x - 3 ) ( 9 x - 2 ) \end{aligned}\)

Contestar

\(( 2 x - 3 ) ( 9 x - 2 )\)

Ejemplo\(\PageIndex{12}\):

Factor usando el método AC:\(4 x ^ { 2 } y ^ { 2 } - 7 x y - 15\).

Solución

Aquí\(a=4, b= -7\), y\(c=-15\).

\(\begin{aligned} a c & = 4 ( - 15 ) \\ & = - 60 \end{aligned}\)

Factorizar\(−60\) y buscar factores cuya suma sea\(−7\).

\(\begin{aligned} - 60 & = 1 ( - 60 ) \\ & = 2 ( - 30 ) \\ & = 3 ( - 20 ) \\ & = 4 ( - 15 ) \\ & = \color{OliveGreen}{5 ( - 12 )}\:\:\color{Cerulean}{✓} \\ & = 6 ( - 10 ) \end{aligned}\)

La suma de factores\(5\) y\(−12\) es igual al coeficiente medio,\(−7\). Reemplazar\(−7xy\) con\(5xy−12xy\).

\(\begin{aligned} 4 x ^ { 2 } y ^ { 2 } - 7 x y - 15 & = 4 x ^ { 2 } y ^ { 2 } + 5 x y - 12 x y - 15\quad\color{Cerulean}{Factor\:by\:grouping.} \\ & = x y ( 4 x y + 5 ) - 3 ( 4 x y + 5 ) \\ & = ( 4 x y + 5 ) ( x y - 3 ) \end{aligned}\)

Contestar

\[( 4 x y + 5 ) ( x y - 3 ).\]

El cheque se deja al lector.

Si los factores de\(ac\) no se pueden encontrar para sumar\(b\) entonces el trinomio es primo.

Claves para llevar

• Si un trinomio de la forma\(x^{2}+bx+c\) factores en el producto de dos binomios, entonces el coeficiente del término medio es la suma de factores del último término.
• Si un trinomio de la forma\(ax^{2}+bx+c\) factores en el producto de dos binomios, entonces el coeficiente del término medio será la suma de ciertos productos de factores del primer y último término.
• Si el trinomio tiene un mayor factor común, entonces es una mejor práctica factorizar primero el GCF antes de intentar factorizarlo en un producto de binomios.
• Si el coeficiente principal de un trinomio es negativo, entonces es una buena práctica factorizar primero ese factor negativo antes de intentar factorizar el trinomio.
• El factoraje es una de las habilidades más importantes que se requieren en álgebra. Por esta razón, debes practicar trabajar tantos problemas como sea necesario para llegar a ser competente.

Ejercicio\(\PageIndex{3}\)

Factor.

1. \(x ^ { 2 } + 5 x - 6\)
2. \(x ^ { 2 } + 5 x + 6\)
3. \(x ^ { 2 } + 4 x - 12\)
4. \(x ^ { 2 } + 3 x - 18\)
5. \(x ^ { 2 } - 14 x + 48\)
6. \(x ^ { 2 } - 15 x + 54\)
7. \(x ^ { 2 } + 11 x - 30\)
8. \(x ^ { 2 } - 2 x + 24\)
9. \(x ^ { 2 } - 18 x + 81\)
10. \(x ^ { 2 } - 22 x + 121\)
11. \(x ^ { 2 } - x y - 20 y ^ { 2 }\)
12. \(x ^ { 2 } + 10 x y + 9 y ^ { 2 }\)
13. \(x ^ { 2 } y ^ { 2 } + 5 x y - 50\)
14. \(x ^ { 2 } y ^ { 2 } - 16 x y + 48\)
15. \(a ^ { 2 } - 6 a b - 72 b ^ { 2 }\)
16. \(a ^ { 2 } - 21 a b + 80 b ^ { 2 }\)
17. \(u ^ { 2 } + 14 u v - 32 v ^ { 2 }\)
18. \(m ^ { 2 } + 7 m n - 98 n ^ { 2 }\)
19. \(( x + y ) ^ { 2 } - 2 ( x + y ) - 8\)
20. \(( x - y ) ^ { 2 } - 2 ( x - y ) - 15\)
21. \(x ^ { 4 } - 7 x ^ { 2 } - 8\)
22. \(x ^ { 4 } + 13 x ^ { 2 } + 30\)
23. \(x ^ { 4 } - 8 x ^ { 2 } - 48\)
24. \(x ^ { 4 } + 25 x ^ { 2 } + 24\)
25. \(y ^ { 4 } - 20 y ^ { 2 } + 100\)
26. \(y ^ { 4 } + 14 y ^ { 2 } + 49\)
27. \(x ^ { 4 } + 3 x ^ { 2 } y ^ { 2 } + 2 y ^ { 4 }\)
28. \(x ^ { 4 } - 8 x ^ { 2 } y ^ { 2 } + 15 y ^ { 4 }\)
29. \(a ^ { 4 } b ^ { 4 } - 4 a ^ { 2 } b ^ { 2 } + 4\)
30. \(a ^ { 4 } + 6 a ^ { 2 } b ^ { 2 } + 9 b ^ { 4 }\)
31. \(x ^ { 6 } - 18 x ^ { 3 } - 40\)
32. \(x ^ { 6 } + 18 x ^ { 3 } + 45\)
33. \(x ^ { 6 } - x ^ { 3 } y ^ { 3 } - 6 y ^ { 6 }\)
34. \(x ^ { 6 } + x ^ { 3 } y ^ { 3 } - 20 y ^ { 6 }\)
35. \(x ^ { 6 } y ^ { 6 } + 2 x ^ { 3 } y ^ { 3 } - 15\)
36. \(x ^ { 6 } y ^ { 6 } + 16 x ^ { 3 } y ^ { 3 } + 48\)
37. \(x ^ { 2 n } + 12 x ^ { n } + 32\)
38. \(x ^ { 2 n } + 41 x ^ { n } + 40\)
39. \(x ^ { 2 n } + 2 a x ^ { n } + a ^ { 2 }\)
40. \(x ^ { 2 n } - 2 a x ^ { n } + a ^ { 2 }\)

Contestar

1. \(( x - 1 ) ( x + 6 )\)

3. \(( x - 2 ) ( x + 6 )\)

5. \(( x - 6 ) ( x - 8 )\)

7. Prime

9. \(( x - 9 ) ^ { 2 }\)

11. \(( x - 5 y ) ( x + 4 y )\)

13. \(( x y - 5 ) ( x y + 10 )\)

15. \(( a + 6 b ) ( a - 12 b )\)

17. \(( u - 2 v ) ( u + 16 v )\)

19. \(( x + y - 4 ) ( x + y + 2 )\)

21. \(\left( x ^ { 2 } - 8 \right) \left( x ^ { 2 } + 1 \right)\)

23. \(\left( x ^ { 2 } + 4 \right) \left( x ^ { 2 } - 12 \right)\)

25. \(\left( y ^ { 2 } - 10 \right) ^ { 2 }\)

27. \(\left( x ^ { 2 } + y ^ { 2 } \right) \left( x ^ { 2 } + 2 y ^ { 2 } \right)\)

29. \(\left( a ^ { 2 } b ^ { 2 } - 2 \right) ^ { 2 }\)

31. \(\left( x ^ { 3 } - 20 \right) \left( x ^ { 3 } + 2 \right)\)

33. \(\left( x ^ { 3 } + 2 y ^ { 3 } \right) \left( x ^ { 3 } - 3 y ^ { 3 } \right)\)

35. \(\left( x ^ { 3 } y ^ { 3 } - 3 \right) \left( x ^ { 3 } y ^ { 3 } + 5 \right)\)

37. \(\left( x ^ { n } + 4 \right) \left( x ^ { n } + 8 \right)\)

39. \(\left( x ^ { n } + a \right) ^ { 2 }\)

Ejercicio\(\PageIndex{4}\)

Factor.

1. \(3 x ^ { 2 } + 20 x - 7\)
2. \(2 x ^ { 2 } - 9 x - 5\)
3. \(6 a ^ { 2 } + 13 a + 6\)
4. \(4 a ^ { 2 } + 11 a + 6\)
5. \(6 x ^ { 2 } + 7 x - 10\)
6. \(4 x ^ { 2 } - 25 x + 6\)
7. \(24 y ^ { 2 } - 35 y + 4\)
8. \(10 y ^ { 2 } - 23 y + 12\)
9. \(14 x ^ { 2 } - 11 x + 9\)
10. \(9 x ^ { 2 } + 6 x + 8\)
11. \(4 x ^ { 2 } - 28 x + 49\)
12. \(36 x ^ { 2 } - 60 x + 25\)
13. \(27 x ^ { 2 } - 6 x - 8\)
14. \(24 x ^ { 2 } + 17 x - 20\)
15. \(6 x ^ { 2 } + 23 x y - 4 y ^ { 2 }\)
16. \(10 x ^ { 2 } - 21 x y - 27 y ^ { 2 }\)
17. \(8 a ^ { 2 } b ^ { 2 } - 18 a b + 9\)
18. \(12 a ^ { 2 } b ^ { 2 } - a b - 20\)
19. \(8 u ^ { 2 } - 26 u v + 15 v ^ { 2 }\)
20. \(24 m ^ { 2 } - 26 m n + 5 n ^ { 2 }\)
21. \(4 a ^ { 2 } - 12 a b + 9 b ^ { 2 }\)
22. \(16 a ^ { 2 } + 40 a b + 25 b ^ { 2 }\)
23. \(5 ( x + y ) ^ { 2 } - 9 ( x + y ) + 4\)
24. \(7 ( x - y ) ^ { 2 } + 15 ( x - y ) - 18\)
25. \(7 x ^ { 4 } - 22 x ^ { 2 } + 3\)
26. \(5 x ^ { 4 } - 41 x ^ { 2 } + 8\)
27. \(4 y ^ { 6 } - 3 y ^ { 3 } - 10\)
28. \(12 y ^ { 6 } + 4 y ^ { 3 } - 5\)
29. \(5 a ^ { 4 } b ^ { 4 } - a ^ { 2 } b ^ { 2 } - 18\)
30. \(21 a ^ { 4 } b ^ { 4 } + 5 a ^ { 2 } b ^ { 2 } - 4\)
31. \(6 x ^ { 6 } y ^ { 6 } + 17 x ^ { 3 } y ^ { 3 } + 10\)
32. \(16 x ^ { 6 } y ^ { 6 } + 46 x ^ { 3 } y ^ { 3 } + 15\)
33. \(8 x ^ { 2 n } - 10 x ^ { n } - 25\)
34. \(30 x ^ { 2 n } - 11 x ^ { n } - 6\)
35. \(36 x ^ { 2 n } + 12 a x ^ { n } + a ^ { 2 }\)
36. \(9 x ^ { 2 n } - 12 a x ^ { n } + 4 a ^ { 2 }\)
37. \(- 3 x ^ { 2 } + 14 x + 5\)
38. \(- 2 x ^ { 2 } + 13 x - 20\)
39. \(- x ^ { 2 } - 10 x + 24\)
40. \(- x ^ { 2 } + 8 x + 48\)
41. \(54 - 12 x - 2 x ^ { 2 }\)
42. \(60 + 5 x - 5 x ^ { 2 }\)
43. \(4 x ^ { 3 } + 16 x ^ { 2 } + 20 x\)
44. \(2 x ^ { 4 } - 12 x ^ { 3 } + 14 x ^ { 2 }\)
45. \(2 x ^ { 3 } - 8 x ^ { 2 } y - 24 x y ^ { 2 }\)
46. \(6 x ^ { 3 } - 9 x ^ { 2 } y - 6 x y ^ { 2 }\)
47. \(4 a ^ { 3 } b - 4 a ^ { 2 } b ^ { 2 } - 24 a b ^ { 3 }\)
48. \(15 a ^ { 4 } b - 33 a ^ { 3 } b ^ { 2 } + 6 a ^ { 2 } b ^ { 3 }\)
49. \(3 x ^ { 5 } y + 30 x ^ { 3 } y ^ { 3 } + 75 x y ^ { 5 }\)
50. \(45 x ^ { 5 } y ^ { 2 } - 60 x ^ { 3 } y ^ { 4 } + 20 x y ^ { 6 }\)

Contestar

1. \(( 3 x - 1 ) ( x + 7 )\)

3. \(( 2 a + 3 ) ( 3 a + 2 )\)

5. \(( 6 x - 5 ) ( x + 2 )\)

7. \(( 8 y - 1 ) ( 3 y - 4 )\)

9. Prime

11. \(( 2 x - 7 ) ^ { 2 }\)

13. \(( 9 x + 4 ) ( 3 x - 2 )\)

15. \(( 6 x - y ) ( x + 4 y )\)

17. \(( 4 a b - 3 ) ( 2 a b - 3 )\)

19. \(( 2 u - 5 v ) ( 4 u - 3 v )\)

21. \(( 2 a - 3 b ) ^ { 2 }\)

23. \(( x + y - 1 ) ( 5 x + 5 y - 4 )\)

25. \(\left( x ^ { 2 } - 3 \right) \left( 7 x ^ { 2 } - 1 \right)\)

27. \(\left( y ^ { 3 } - 2 \right) \left( 4 y ^ { 3 } + 5 \right)\)

29. \(\left( a ^ { 2 } b ^ { 2 } - 2 \right) \left( 5 a ^ { 2 } b ^ { 2 } + 9 \right)\)

31. \(\left( 6 x ^ { 3 } y ^ { 3 } + 5 \right) \left( x ^ { 3 } y ^ { 3 } + 2 \right)\)

33. \(\left( 2 x ^ { n } - 5 \right) \left( 4 x ^ { n } + 5 \right)\)

35. \(\left( 6 x ^ { n } + a \right) ^ { 2 }\)

37. \(- ( x - 5 ) ( 3 x + 1 )\)

39. \(- ( x - 2 ) ( x + 12 )\)

41. \(- 2 ( x - 3 ) ( x + 9 )\)

43. \(4 x \left( x ^ { 2 } + 4 x + 5 \right)\)

45. \(2 x ( x + 2 y ) ( x - 6 y )\)

47. \(4 a b ( a - 3 b ) ( a + 2 b )\)

49. \(3 x y \left( x ^ { 2 } + 5 y ^ { 2 } \right) ^ { 2 }\)

Ejercicio\(\PageIndex{5}\)

Factor.

1. \(4 - 25 x ^ { 2 }\)
2. \(8 x ^ { 3 } - y ^ { 3 }\)
3. \(9 x ^ { 2 } - 12 x y + 4 y ^ { 2 }\)
4. \(30 a ^ { 2 } - 57 a b - 6 b ^ { 2 }\)
5. \(10 a ^ { 2 } - 5 a - 6 a b + 3 b\)
6. \(3 x ^ { 3 } - 4 x ^ { 2 } + 9 x - 12\)
7. \(x ^ { 2 } + 4 y ^ { 2 }\)
8. \(x ^ { 2 } - x + 2\)
9. \(15 a ^ { 3 } b ^ { 2 } + 6 a ^ { 2 } b ^ { 3 } - 3 a b ^ { 4 }\)
10. \(54 x ^ { 2 } - 63 x\)

Contestar

1. \(( 2 - 5 x ) ( 2 + 5 x )\)

3. \(( 3 x - 2 y ) ^ { 2 }\)

5. \(( 2 a - 1 ) ( 5 a - 3 b )\)

7. Prime

9. \(3 a b ^ { 2 } \left( 5 a ^ { 2 } + 2 a b - b ^ { 2 } \right)\)

Ejercicio\(\PageIndex{6}\)

1. Crea tu propio trinomio de la forma\(ax^{2} + bx + c\) que factoriza. Compártelo, junto con la solución, en el panel de discusión.
2. Crear un trinomio de la forma\(ax^{2} + bx + c\) que no factoriza y compartirlo junto con la razón por la que no factoriza.

Contestar

1. La respuesta puede variar

Notas al pie

¹⁸ Describe el método de factorizar un trinomio comprobando sistemáticamente los factores para ver si su producto es el trinomio original.

¹⁹ Método utilizado para factorizar trinomios sustituyendo el término medio por dos términos que permiten factorizar el polinomio resultante de cuatro términos por agrupación.