4.4: Resolver ecuaciones polinómicas por factorización

Última actualización
Guardar como PDF

Page ID: 109811

Anonymous
LibreTexts

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Revisar estrategias generales para la factorización.
Resolver ecuaciones polinómicas por factorización.
Encontrar raíces de una función polinómica.
Encontrar ecuaciones polinómicas dadas las soluciones.

Revisión de Estrategias Generales de Factoring

Hemos aprendido diversas técnicas para factorizar polinomios con hasta cuatro términos. El reto es identificar el tipo de polinomio y luego decidir qué método aplicar. A continuación se describe una guía general para factorizar polinomios.

lineamientos generales para factorizar polinomios

Paso 1: Verificar factores comunes. Si los términos tienen factores comunes, entonces factorizar el mayor factor común (GCF).

Paso 2: Determinar el número de términos en el polinomio.

Factorizar polinomios de cuatro términos por agrupación.
Trinomios factoriales (3 términos) usando “ensayo y error” o el método AC.
Binomios factoriales (2 términos) utilizando los siguientes productos especiales:
- Diferencia de cuadrados:\(a^{2}−b^{2}=(a+b)(a−b)\)
- Suma de cuadrados:\(a^{2}+b^{2}\) sin fórmula general
- Diferencia de cubos:\(a^{3}−b^{3}=(a−b)(a^{2}+ab+b^{2})\)
- Suma de cubos:\(a^{3}+b^{3}=(a+b)(a^{2}−ab+b^{2})\)

Paso 3: Busque factores que se puedan factorizar más.

Paso 4: Verificar multiplicando.

Si un binomio es tanto una diferencia de cuadrados como una diferencia de cubos, entonces primero factorizarlo como diferencia de cuadrados. Esto dará como resultado una factorización más completa. Además, no todos los polinomios con coeficientes enteros factor. Cuando este es el caso, decimos que el polinomio es primo.

Si una expresión tiene un GCF, entonces factorizar esto primero. Hacerlo a menudo se pasa por alto y, por lo general, resulta en factores con los que es más fácil trabajar. Además, busque los factores resultantes para factorizar aún más; muchos problemas de factorización requieren más de un paso. Un polinomio es completamente factorizado cuando ninguno de los factores puede ser factorizado más.

Ejemplo\(\PageIndex{1}\):

Factor\(54 x ^ { 4 } - 36 x ^ { 3 } - 24 x ^ { 2 } + 16 x\).

Solución

Este polinomio de cuatro términos tiene un GCF de\(2x\). Factorial esto primero.

\(54 x ^ { 4 } - 36 x ^ { 3 } - 24 x ^ { 2 } + 16 x = 2 x \left( 27 x ^ { 3 } - 18 x ^ { 2 } - 12 x + 8 \right)\)

Ahora factorizar el polinomio resultante de cuatro términos por agrupación y buscar factores resultantes para factorizar más.

Contestar

\(2 x ( 3 x - 2 ) ^ { 2 } ( 3 x + 2 )\). El cheque se deja al lector.

Ejemplo\(\PageIndex{2}\):

Factor:\(x ^ { 4 } - 3 x ^ { 2 } - 4\).

Solución

Este trinomio no tiene un GCF.

\(\begin{aligned} x ^ { 4 } - 3 x ^ { 2 } - 4 & = \left( x ^ { 2 } \quad\right) \left( x ^ { 2 }\quad \right) \\ & = \left( x ^ { 2 } + 1 \right) \left( x ^ { 2 } - 4 \right) \quad\color{Cerulean} { Difference\: of\: squares } \\ & = \left( x ^ { 2 } + 1 \right) ( x + 2 ) ( x - 2 ) \end{aligned}\)

El factor\(\left( x ^ { 2 } + 1 \right)\) es primo y el trinomio está completamente factorizado.

Respuesta:

\(\left( x ^ { 2 } + 1 \right) ( x + 2 ) ( x - 2 )\)

Ejemplo\(\PageIndex{3}\):

Factor:\(x ^ { 6 } + 6 x ^ { 3 } - 16\).

Solución

Comience por factorizar\(x ^ { 6 } = x ^ { 3 } \cdot x ^ { 3 }\) y busque los factores de\(16\) que se suman a\(6\).

\(\begin{aligned} x ^ { 6 } + 6 x ^ { 3 } - 16 & = \left( x ^ { 3 }\quad \right) \left( x ^ { 3 }\quad \right) \\ & = \left( x ^ { 3 } - 2 \right) \left( x ^ { 3 } + 8 \right)\quad \color{Cerulean} { sum\:of\:cubes } \\ & = \left( x ^ { 3 } - 2 \right) ( x + 2 ) \left( x ^ { 2 } - 2 x + 4 \right) \end{aligned}\)

El factor\(\left( x ^ { 3 } - 2 \right)\) no se puede factorizar más usando números enteros y la factorización es completa.

Respuesta:

\(\left( x ^ { 3 } - 2 \right) ( x + 2 ) \left( x ^ { 2 } + 2 x + 4 \right)\)

Ejercicio\(\PageIndex{1}\)

Factor:\(9 x ^ { 4 } + 17 x ^ { 2 } - 2\)

Contestar

\(( 3 x + 1 ) ( 3 x - 1 ) \left( x ^ { 2 } + 2 \right)\)

www.youtube.com/v/lsap8_ugux0

Resolver ecuaciones polinomiales por factorización

En esta sección, revisaremos una técnica que puede ser utilizada para resolver ciertas ecuaciones polinómicas. Comenzamos con la propiedad cero producto ²⁰:

\(a⋅b=0\)si y solo si\(a=0\) o\(b=0\)

La propiedad de producto cero es verdadera para cualquier número de factores que componen una ecuación. Es decir, si algún producto es igual a cero, entonces al menos uno de los factores variables debe ser igual a cero. Si una expresión es igual a cero y se puede factorizar en factores lineales, entonces podremos establecer cada factor igual a cero y resolver para cada ecuación.

Ejemplo\(\PageIndex{4}\)

Resolver:\(2 x ( x - 4 ) ( 5 x + 3 ) = 0\).

Solución

Establezca cada factor variable igual a cero y resuelva.

\(\begin{aligned} 2 x & = 0 \\ \frac { 2 x } { \color{Cerulean}{2} } & = \frac { 0 } {\color{Cerulean}{ 2} } \\ x & = 0 \end{aligned}\)o\(\begin{aligned} x - 4 & = 0 \\ x & = 4 \end{aligned}\) o\(\begin{aligned} 5 x + 3 & = 0 \\ \frac { 5 x } { \color{Cerulean}{5} } & = \frac { - 3 } {\color{Cerulean}{ 5} } \\ x & = - \frac { 3 } { 5 } \end{aligned}\)

Para comprobar que se trata de soluciones podemos sustituir de nuevo en la ecuación original para ver si obtenemos una declaración verdadera. Tenga en cuenta que cada solución produce un factor cero. Esto se deja en manos del lector.

Respuesta:

Las soluciones son\(0, 4\), y\(\frac{−3}{5}\).

Por supuesto, la mayoría de las ecuaciones no se darán en forma factorizada.

Ejemplo\(\PageIndex{5}\)

Resolver:\(4 x ^ { 3 } - x ^ { 2 } - 100 x + 25 = 0\).

Solución

Comience factorizando completamente el lado izquierdo.

\(\begin{aligned} 4 x ^ { 3 } - x ^ { 2 } - 100 x + 25 & = 0 \quad\color{Cerulean}{Factor\:by\:grouping.} \\ x ^ { 2 } ( 4 x - 1 ) - 25 ( 4 x - 1 ) & = 0 \\ ( 4 x - 1 ) \left( x ^ { 2 } - 25 \right) & = 0\quad\color{Cerulean}{Factor\:as\:a\:difference\:of\:squares.} \\ ( 4 x - 1 ) ( x + 5 ) ( x - 5 ) & = 0 \end{aligned}\)

Establezca cada factor igual a cero y resuelva.

\(\begin{array} { r } { 4 x - 1 = 0 } \\ { 4 x = 1 } \\ { x = \frac { 1 } { 4 } } \end{array}\)o\(\begin{aligned} x + 5 & = 0 \\ x & = - 5 \end{aligned}\) o\(\begin{aligned} x - 5 & = 0 \\ x & = 5 \end{aligned}\)

Respuesta:

Las soluciones son\(\frac{1}{4}, −5\), y\(5\).

El uso de la propiedad de cero producto después de factorizar una ecuación que es igual a cero es la clave de esta técnica. Sin embargo, la ecuación puede no ser dada igual a cero, por lo que puede haber algunos pasos preliminares antes de factorizar. Los pasos requeridos para resolver por factorización ²¹ se describen en el siguiente ejemplo.

Ejemplo\(\PageIndex{6}\)

Resolver:\(15 x ^ { 2 } + 3 x - 8 = 5 x - 7\).

Solución

Paso 1: Exprese la ecuación en forma estándar, igual a cero. En este ejemplo, restar\(5x\) y sumar\(7\) a ambos lados.

\(\begin{array} { l } { 15 x ^ { 2 } + 3 x - 8 = 5 x - 7 } \\ { 15 x ^ { 2 } - 2 x - 1 = 0 } \end{array}\)

Paso 2: Factorizar la expresión.

\((3x−1)(5x+1)=0\)

Paso 3: Aplicar la propiedad de cero producto y establecer cada factor variable igual a cero.

\(3x−1=0\)o\(5x+1=0\)

Paso 4: Resolver las ecuaciones lineales resultantes.

\(\begin{array} { r } { 3 x - 1 = 0 } \\ { 3 x = 1 } \\ { x = \frac { 1 } { 3 } } \end{array}\)o\(\begin{aligned} 5 x + 1 & = 0 \\ 5 x & = - 1 \\ x & = - \frac { 1 } { 5 } \end{aligned}\)

Respuesta:

Las soluciones son\(\frac{1}{3}\) y\(\frac{−1}{5}\). El cheque es opcional.

Ejemplo\(\PageIndex{7}\):

Resolver:\((3x+2)(x+1)=4\).

Solución

Esta ecuación cuadrática parece ser factorizada; por lo tanto, podría ser tentador establecer cada factor igual a\(4\). Sin embargo, esto conduciría a resultados incorrectos. Debemos reescribir la ecuación igual a cero, para que podamos aplicar la propiedad zero product.

\(\begin{array} { r } { ( 3 x + 2 ) ( x + 1 ) = 4 } \\ { 3 x ^ { 2 } + 3 x + 2 x + 2 = 4 } \\ { 3 x ^ { 2 } + 5 x + 2 = 4 } \\ { 3 x ^ { 2 } + 5 x - 2 = 0 } \end{array}\)

Una vez que está en forma estándar, podemos factorizar y luego establecer cada factor igual a cero.

\(\begin{array} { c } { ( 3 x - 1 ) ( x + 2 ) = 0 } \\ { 3 x - 1 = 0 \quad \text { or } \quad x + 2 = 0 } \\ \quad\quad{ 3 x = 1 }\quad\quad\quad\:\:\quad x=-2\\ { x = \frac { 1 } { 3 } }\quad\quad\quad\quad\quad\: \end{array}\)

Respuesta:

Las soluciones son\(\frac{1}{3}\) y\(−2\).

Encontrar las raíces de las funciones

Recordemos que cualquier polinomio con una variable es una función y puede escribirse en la forma,

\(f ( x ) = a _ { n } x ^ { n } + a _ { n - 1 } x ^ { n - 1 } + \cdots + a _ { 1 } x + a _ { 0 }\)

Una raíz ²² de una función es un valor en el dominio que da como resultado cero. En otras palabras, las raíces ocurren cuando la función es igual a cero,\(f(x)=0\).

Ejemplo\(\PageIndex{8}\)

Encuentra las raíces:\(f ( x ) = ( x + 2 ) ^ { 2 } - 4\).

Solución

Para encontrar raíces establecemos la función igual a cero y resolvemos.

\(\begin{aligned} f ( x ) & = 0 \\ ( x + 2 ) ^ { 2 } - 4 & = 0 \\ x ^ { 2 } + 4 x + 4 - 4 & = 0 \\ x ^ { 2 } + 4 x & = 0 \\ x ( x + 4 ) & = 0 \end{aligned}\)

A continuación, establezca cada factor igual a cero y resuelva.

\(\begin{aligned} x = 0 \quad \text { or } \quad x + 4 = 0 \\ x = - 4 \end{aligned}\)

Podemos demostrar que estos\(x\) valores son raíces mediante la evaluación.

\(\begin{aligned} f ( 0 ) & = ( 0 + 2 ) ^ { 2 } - 4 \\ & = 4 - 4 \\ & = 0 \color{Cerulean}{✓}\end{aligned}\)\(\begin{aligned} f ( - 4 ) & = ( - 4 + 2 ) ^ { 2 } - 4 \\ & = ( - 2 ) ^ { 2 } - 4 \\ & = 4 - 4 \\ & = 0 \color{Cerulean}{✓}\end{aligned}\)

Respuesta:

Las raíces son\(0\) y\(−4\).

Si graficamos la función en el ejemplo anterior veremos que las raíces corresponden a las\(x\) -intercepciones de la función. Aquí la función\(f\) es una parábola básica desplazada\(2\) unidades hacia la izquierda y\(4\) unidades hacia abajo.

Ejemplo\(\PageIndex{9}\)

Encuentra las raíces:\(f ( x ) = x ^ { 4 } - 5 x ^ { 2 } + 4\).

Solución

Para encontrar raíces establecemos la función igual a cero y resolvemos.

\(\begin{aligned} f ( x ) & = 0 \\ x ^ { 4 } - 5 x ^ { 2 } + 4 & = 0 \\ \left( x ^ { 2 } - 1 \right) \left( x ^ { 2 } - 4 \right) & = 0 \\ ( x + 1 ) ( x - 1 ) ( x + 2 ) ( x - 2 ) & = 0 \end{aligned}\)

A continuación, establezca cada factor igual a cero y resuelva.

\(\begin{aligned} x + 1 & = 0 \\ x & = - 1 \end{aligned}\)o\(\begin{array} { r } { x - 1 = 0 } \\ { x = 1 } \end{array}\) o\(\begin{aligned} x + 2 & = 0 \\ x & = - 2 \end{aligned}\) o\(\begin{aligned} x - 2 & = 0 \\ x & = 2 \end{aligned}\)

Respuesta:

Las raíces son\(−1, 1, −2\), y\(2\).

Graficar la función anterior no está dentro del alcance de este curso. Sin embargo, la gráfica se proporciona a continuación:

Observe que el grado del polinomio es\(4\) y obtuvimos cuatro raíces. En general, para cualquier función polinómica con una variable de grado\(n\), el teorema fundamental del álgebra ²³ garantiza raíces\(n\) reales o menos. Hemos visto que muchos polinomios no factorizan. Esto no implica que las funciones que involucran a estos polinomios infactoriables no tengan raíces reales. De hecho, muchas funciones polinómicas que no factorizan sí tienen soluciones reales. Aprenderemos a encontrar este tipo de raíces a medida que continuemos en nuestro estudio del álgebra.

Ejemplo\(\PageIndex{10}\)

Encuentra las raíces:\(f ( x ) = - x ^ { 2 } + 10 x - 25\).

Solución

Para encontrar raíces establecemos la función igual a cero y resolvemos.

\(\begin{aligned} f ( x ) & = 0 \\ - x ^ { 2 } + 10 x - 25 & = 0 \\ - \left( x ^ { 2 } - 10 x + 25 \right) & = 0 \\ - ( x - 5 ) ( x - 5 ) & = 0 \end{aligned}\)

A continuación, establezca cada factor variable igual a cero y resuelva.

\(\begin{aligned} x - 5 & = 0 \quad\quad\text { or }& x - 5 = 0 \\ & = 5 \quad &x= 5 \end{aligned}\)

Una solución que se repite dos veces se llama doble raíz ²⁴. En este caso, sólo hay una solución.

Respuesta:

La raíz es\(5\).

El ejemplo anterior muestra que una función de grado\(2\) puede tener una raíz. Desde el paso de factorización, vemos que la función se puede escribir

\(f ( x ) = - ( x - 5 ) ^ { 2 }\)

En esta forma, podemos ver una reflexión sobre el\(x\) eje y un desplazamiento hacia las\(5\) unidades de la derecha. El vértice es la\(x\) -intercepción, ilustrando el hecho de que sólo hay una raíz.

Ejercicio\(\PageIndex{2}\)

Encuentra las raíces de\(f ( x ) = x ^ { 3 } + 3 x ^ { 2 } - x - 3\).

Contestar

\(±1, −3\)

www.youtube.com/v/t1shqqhoave

Ejemplo\(\PageIndex{11}\)

Suponiendo condiciones de carretera seca y tiempos de reacción promedio, la distancia de parada segura en pies viene dada por\(d ( x ) = \frac { 1 } { 20 } x ^ { 2 } + x\), donde\(x\) representa la velocidad del automóvil en millas por hora. Determine la velocidad segura del automóvil si espera detenerse en\(40\) pies.

Solución

Se nos pide encontrar la velocidad\(x\) donde la distancia de parada segura\(d(x)=40\) pies.

\(\begin{array} { c } { d ( x ) = 40 } \\ { \frac { 1 } { 20 } x ^ { 2 } + x = 40 } \end{array}\)

Para resolver para\(x\), reescriba la ecuación resultante en forma estándar. En este caso, primero multiplicaremos ambos lados por\(20\) para despejar la fracción.

\(\begin{aligned} \color{Cerulean}{20}\color{black}{ \left( \frac { 1 } { 20 } x ^ { 2 } + x \right)} & = \color{Cerulean}{20}\color{black}{ (} 40 ) \\ x ^ { 2 } + 20 x & = 800 \\ x ^ { 2 } + 20 x - 800 & = 0 \end{aligned}\)

Siguiente factor y luego establecer cada factor igual a cero.

\(\begin{aligned} x ^ { 2 } + 20 x - 800 & = 0 \\ ( x + 40 ) ( x - 20 ) & = 0 \\ x + 40 & = 0\quad or\quad \:x-20=0 \\ x & = - 40\quad \quad\quad\quad x=20 \end{aligned}\)

La respuesta negativa no tiene sentido en el contexto de este problema. Considera que las\(x=20\) millas por hora son la única solución.

Respuesta:

\(20\)millas por hora

Encontrar ecuaciones con soluciones dadas

Podemos usar la propiedad de cero producto para encontrar ecuaciones, dadas las soluciones. Para ello, los pasos para resolver por factorización se realizan a la inversa.

Ejemplo\(\PageIndex{12}\)

Encontrar una ecuación cuadrática con coeficientes enteros, dadas soluciones\(\frac{−3}{2}\) y\(\frac{1}{3}\).

Solución

Dadas las soluciones, podemos determinar dos factores lineales. Para evitar coeficientes fraccionarios, primero limpiamos las fracciones multiplicando ambos lados por el denominador.

\(\begin{aligned} x & = - \frac { 3 } { 2 } \\ 2 x & = - 3 \\ 2 x + 3 & = 0 \end{aligned}\)o\(\begin{aligned} x & = \frac { 1 } { 3 } \\ 3 x & = 1 \\ 3 x - 1 & = 0 \end{aligned}\)

El producto de estos factores lineales es igual a cero cuando\(x=\frac{−3}{2}\) o\(x=\frac{1}{3}\).

\((2x+3)(3x−1)=0\)

Multiplicar los binomios y presentar la ecuación en forma estándar.

\(\begin{array} { r } { 6 x ^ { 2 } - 2 x + 9 x - 3 = 0 } \\ { 6 x ^ { 2 } + 7 x - 3 = 0 } \end{array}\)

Podemos verificar nuestra ecuación sustituyendo las respuestas dadas para ver si obtenemos una declaración verdadera. Además, la ecuación que se encuentra arriba no es única y así el cheque se vuelve esencial cuando nuestra ecuación se ve diferente a la de otra persona, esto se deja como un ejercicio.

Respuesta:

\(6 x ^ { 2 } + 7 x - 3 = 0\)

Ejemplo\(\PageIndex{13}\)

Encontrar una función polinómica con raíces reales\(1, −2\), y\(2\).

Solución

Dadas soluciones a\(f(x)=0\) podemos encontrar factores lineales.

\(\begin{array} { r } { x = 1 } \\ { x - 1 = 0 } \end{array}\)o\(\begin{aligned} x & = - 2 \\ x + 2 & = 0 \end{aligned}\) o\(\begin{aligned} x & = 2 \\ x - 2 & = 0 \end{aligned}\)

Aplicar la propiedad de cero producto y multiplicar.

\(\begin{aligned} ( x - 1 ) ( x + 2 ) ( x - 2 ) & = 0 \\ ( x - 1 ) \left( x ^ { 2 } - 4 \right) & = 0 \\ x ^ { 3 } - 4 x - x ^ { 2 } + 4 & = 0 \\ x ^ { 3 } - x ^ { 2 } - 4 x + 4 & = 0 \end{aligned}\)

Respuesta:

\(f ( x ) = x ^ { 3 } - x ^ { 2 } - 4 x + 4\)

Ejercicio\(\PageIndex{3}\)

Encuentra una ecuación polinómica con coeficientes enteros, soluciones dadas\(\frac{1}{2}\) y\(\frac{−3}{4}\).

Contestar

\(8 x ^ { 2 } + 2 x - 3 = 0\)

www.youtube.com/v/o4cuuwwegdu

Claves para llevar

La factorización y la propiedad de cero productos nos permiten resolver ecuaciones.
Para resolver una ecuación polinómica, primero escríbalo en forma estándar. Una vez que sea igual a cero, factorizarlo y luego establecer cada factor variable igual a cero. Las soluciones a las ecuaciones resultantes son las soluciones a la original.
No todas las ecuaciones polinómicas pueden resolverse factorizando. Aprenderemos a resolver ecuaciones polinómicas que no factorizan más adelante en el curso.
Una función polinómica puede tener como máximo un número de raíces reales igual a su grado. Para encontrar raíces de una función, ponla igual a cero y resolver.
Para encontrar una ecuación polinómica con soluciones dadas, realice el proceso de resolución factorizando a la inversa.

Ejercicio\(\PageIndex{4}\)

Factor completamente.

\(50 x ^ { 2 } - 18\)
\(12 x ^ { 3 } - 3 x\)
\(10 x ^ { 3 } + 65 x ^ { 2 } - 35 x\)
\(15 x ^ { 4 } + 7 x ^ { 3 } - 4 x ^ { 2 }\)
\(6 a ^ { 4 } b - 15 a ^ { 3 } b ^ { 2 } - 9 a ^ { 2 } b ^ { 3 }\)
\(8 a ^ { 3 } b - 44 a ^ { 2 } b ^ { 2 } + 20 a b ^ { 3 }\)
\(36 x ^ { 4 } - 72 x ^ { 3 } - 4 x ^ { 2 } + 8 x\)
\(20 x ^ { 4 } + 60 x ^ { 3 } - 5 x ^ { 2 } - 15 x\)
\(3 x ^ { 5 } + 2 x ^ { 4 } - 12 x ^ { 3 } - 8 x ^ { 2 }\)
\(10 x ^ { 5 } - 4 x ^ { 4 } - 90 x ^ { 3 } + 36 x ^ { 2 }\)
\(x ^ { 4 } - 23 x ^ { 2 } - 50\)
\(2 x ^ { 4 } - 31 x ^ { 2 } - 16\)
\(- 2 x ^ { 5 } - 6 x ^ { 3 } + 8 x\)
\(- 36 x ^ { 5 } + 69 x ^ { 3 } + 27 x\)
\(54 x ^ { 5 } - 78 x ^ { 3 } + 24 x\)
\(4 x ^ { 6 } - 65 x ^ { 4 } + 16 x ^ { 2 }\)
\(x ^ { 6 } - 7 x ^ { 3 } - 8\)
\(x ^ { 6 } - 25 x ^ { 3 } - 54\)
\(3 x ^ { 6 } + 4 x ^ { 3 } + 1\)
\(27 x ^ { 6 } - 28 x ^ { 3 } + 1\)

Contestar

1. \(2 ( 5 x + 3 ) ( 5 x - 3 )\)

3. \(5 x ( x + 7 ) ( 2 x - 1 )\)

5. \(3 a ^ { 2 } b ( 2 a + b ) ( a - 3 b )\)

7. \(4 x ( x - 2 ) ( 3 x + 1 ) ( 3 x - 1 )\)

9. \(x ^ { 2 } ( 3 x + 2 ) ( x + 2 ) ( x - 2 )\)

11. \(\left( x ^ { 2 } + 2 \right) ( x + 5 ) ( x - 5 )\)

13. \(- 2 x \left( x ^ { 2 } + 4 \right) ( x - 1 ) ( x + 1 )\)

15. \(6 x ( x + 1 ) ( x - 1 ) ( 3 x + 2 ) ( 3 x - 2 )\)

17. \(( x + 1 ) \left( x ^ { 2 } - x + 1 \right) ( x - 2 ) \left( x ^ { 2 } + 2 x + 4 \right)\)

19. \(\left( 3 x ^ { 3 } + 1 \right) ( x + 1 ) \left( x ^ { 2 } - x + 1 \right)\)

Ejercicio\(\PageIndex{5}\)

Resolver.

\(( 6 x - 5 ) ( x + 7 ) = 0\)
\(( x + 9 ) ( 3 x - 8 ) = 0\)
\(5 x ( 2 x - 5 ) ( 3 x + 1 ) = 0\)
\(4 x ( 5 x - 1 ) ( 2 x + 3 ) = 0\)
\(( x - 1 ) ( 2 x + 1 ) ( 3 x - 5 ) = 0\)
\(( x + 6 ) ( 5 x - 2 ) ( 2 x + 9 ) = 0\)
\(( x + 4 ) ( x - 2 ) = 16\)
\(( x + 1 ) ( x - 7 ) = 9\)
\(( 6 x + 1 ) ( x + 1 ) = 6\)
\(( 2 x - 1 ) ( x - 4 ) = 39\)
\(x ^ { 2 } - 15 x + 50 = 0\)
\(x ^ { 2 } + 10 x - 24 = 0\)
\(3 x ^ { 2 } + 2 x - 5 = 0\)
\(2 x ^ { 2 } + 9 x + 7 = 0\)
\(\frac { 1 } { 10 } x ^ { 2 } - \frac { 7 } { 15 } x - \frac { 1 } { 6 } = 0\)
\(\frac { 1 } { 4 } - \frac { 4 } { 9 } x ^ { 2 } = 0\)
\(6 x ^ { 2 } - 5 x - 2 = 30 x + 4\)
\(6 x ^ { 2 } - 9 x + 15 = 20 x - 13\)
\(5 x ^ { 2 } - 23 x + 12 = 4 ( 5 x - 3 )\)
\(4 x ^ { 2 } + 5 x - 5 = 15 ( 3 - 2 x )\)
\(( x + 6 ) ( x - 10 ) = 4 ( x - 18 )\)
\(( x + 4 ) ( x - 6 ) = 2 ( x + 4 )\)
\(4 x ^ { 3 } - 14 x ^ { 2 } - 30 x = 0\)
\(9 x ^ { 3 } + 48 x ^ { 2 } - 36 x = 0\)
\(\frac { 1 } { 3 } x ^ { 3 } - \frac { 3 } { 4 } x = 0\)
\(\frac { 1 } { 2 } x ^ { 3 } - \frac { 1 } { 50 } x = 0\)
\(- 10 x ^ { 3 } - 28 x ^ { 2 } + 48 x = 0\)
\(- 2 x ^ { 3 } + 15 x ^ { 2 } + 50 x = 0\)
\(2 x ^ { 3 } - x ^ { 2 } - 72 x + 36 = 0\)
\(4 x ^ { 3 } - 32 x ^ { 2 } - 9 x + 72 = 0\)
\(45 x ^ { 3 } - 9 x ^ { 2 } - 5 x + 1 = 0\)
\(x ^ { 3 } - 3 x ^ { 2 } - x + 3 = 0\)
\(x ^ { 4 } - 5 x ^ { 2 } + 4 = 0\)
\(4 x ^ { 4 } - 37 x ^ { 2 } + 9 = 0\)

Contestar

1. \(- 7 , \frac { 5 } { 6 }\)

3. \(0 , \frac { 5 } { 2 } , - \frac { 1 } { 3 }\)

5. \(- \frac { 1 } { 2 } , 1 , \frac { 5 } { 3 }\)

7. \(- 6,4\)

9. \(- \frac { 5 } { 3 } , \frac { 1 } { 2 }\)

11. \(5,10\)

13. \(- \frac { 5 } { 3 } , 1\)

15. \(- \frac { 1 } { 3 } , 5\)

17. \(- \frac { 1 } { 6 } , 6\)

19. \(\frac { 3 } { 5 } , 8\)

21. \(2,6\)

23. \(0 , - \frac { 3 } { 2 } , 5\)

25. \(0 , \pm \frac { 3 } { 2 }\)

27. \(- 4,0 , \frac { 6 } { 5 }\)

29. \(\pm 6 , \frac { 1 } { 2 }\)

31. \(\pm \frac { 1 } { 3 } , \frac { 1 } { 5 }\)

33. \(\pm 1 , \pm 2\)

Ejercicio\(\PageIndex{6}\)

Encuentra las raíces de las funciones dadas.

\(f ( x ) = x ^ { 2 } + 10 x - 24\)
\(f ( x ) = x ^ { 2 } - 14 x + 48\)
\(f ( x ) = - 2 x ^ { 2 } + 7 x + 4\)
\(f ( x ) = - 3 x ^ { 2 } + 14 x + 5\)
\(f ( x ) = 16 x ^ { 2 } - 40 x + 25\)
\(f ( x ) = 9 x ^ { 2 } - 12 x + 4\)
\(g ( x ) = 8 x ^ { 2 } + 3 x\)
\(g ( x ) = 5 x ^ { 2 } - 30 x\)
\(p ( x ) = 64 x ^ { 2 } - 1\)
\(q ( x ) = 4 x ^ { 2 } - 121\)
\(f ( x ) = \frac { 1 } { 5 } x ^ { 3 } - 1 x ^ { 2 } - \frac { 1 } { 20 } x + \frac { 1 } { 4 }\)
\(f ( x ) = \frac { 1 } { 3 } x ^ { 3 } + \frac { 1 } { 2 } x ^ { 2 } - \frac { 4 } { 3 } x - 2\)
\(g ( x ) = x ^ { 4 } - 13 x ^ { 2 } + 36\)
\(g ( x ) = 4 x ^ { 4 } - 13 x ^ { 2 } + 9\)
\(f ( x ) = ( x + 5 ) ^ { 2 } - 1\)
\(g ( x ) = - ( x + 5 ) ^ { 2 } + 9\)
\(f ( x ) = - ( 3 x - 5 ) ^ { 2 }\)
\(g ( x ) = - ( x + 2 ) ^ { 2 } + 4\)

Contestar

1. \(2 , - 12\)

3. \(- \frac { 1 } { 2 } , 4\)

5. \(\frac { 5 } { 4 }\)

7. \(- \frac { 3 } { 8 } , 0\)

9. \(\pm \frac { 1 } { 8 }\)

11. \(\pm \frac { 1 } { 2 } , 5\)

13. \(\pm 2 , \pm 3\)

15. \(- 6 , - 4\)

17. \(\frac { 5 } { 3 }\)

Ejercicio\(\PageIndex{7}\)

Dada la gráfica de una función, determinar las raíces reales.

5. Los lados de un cuadrado miden\(x − 2\) unidades. Si el área es unidades\(36\) cuadradas, entonces encuentra\(x\).

6. Los lados de un triángulo rectángulo tienen longitudes que son números enteros pares consecutivos. Encuentra las longitudes de cada lado. (Pista: Aplicar el teorema de Pitágoras)

7. El beneficio en dólares generado por la producción y venta de n bicicletas por semana viene dado por la fórmula\(P ( n ) = - 5 n ^ { 2 } + 400 n - 6000\). ¿Cuántas bicicletas se deben producir y vender para igualar?

8. La altura en pies de un objeto caído desde la parte superior de un edificio\(64\) -foot viene dada por\(h ( t ) = - 16 t ^ { 2 } + 64\) donde\(t\) representa el tiempo en segundos después de que se cae. ¿Cuánto tiempo tardará en golpear el suelo?

9. Se puede hacer una caja cortando las esquinas y plegando los bordes de una hoja cuadrada de cartón. Se da una plantilla para una caja de cartón de 2 pulgadas de altura.

¿Cuál es la longitud de cada lado de la hoja de cartón si el volumen de la caja va a ser pulgadas\(98\) cúbicas?

10. La altura de un triángulo es\(4\) centímetros menos del doble de la longitud de su base. Si el área total del triángulo es de centímetros\(48\) cuadrados, entonces encuentra las longitudes de la base y la altura.

11. Se debe colocar un borde uniforme alrededor de una imagen\(8 × 10\) de una pulgada.

Si el área total incluyendo el borde debe ser de pulgadas\(168\) cuadradas, entonces, ¿qué tan ancho debe ser el borde?

12. El área de un marco de fotos que incluye un borde\(3\) de pulgadas de ancho es de pulgadas\(120\) cuadradas.

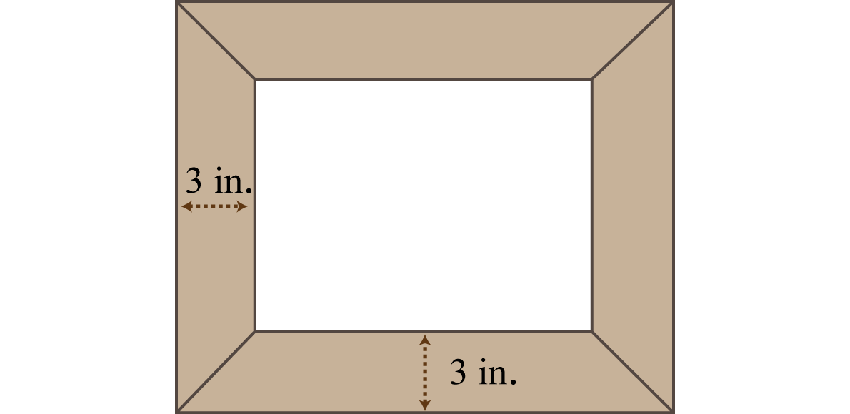
Si el ancho del área interior es\(2\) pulgadas menos que su longitud, entonces encuentre las dimensiones del área interior.

13. Suponiendo condiciones de carretera seca y tiempos de reacción promedio, la distancia de parada segura en pies viene dada por\(d ( x ) = \frac { 1 } { 20 } x ^ { 2 } + x\) donde\(x\) representa la velocidad del automóvil en millas por hora. Determine la velocidad segura del automóvil si espera detenerse en\(75\) pies.

14. Una empresa manufacturera ha determinado que el ingreso diario en miles de dólares viene dado por la fórmula\(R ( n ) = 12 n - 0.6 n ^ { 2 }\) donde\(n\) representa el número de paletas de producto vendido\((0 ≤ n < 20)\). Determinar el número de paletas vendidas en un día si los ingresos fueron de\(45\) mil dólares.

Contestar

1. \(- 3 , - 1,0,2\)

3. \(- 2,3\)

5. \(8\)unidades

7. \(20\)o\(60\) bicicletas

9. \(11\)en

11. \(2\)pulgadas

13. \(30\)millas por hora

Ejercicio\(\PageIndex{8}\)

Encontrar una ecuación polinómica con las soluciones dadas.

\(-3,5\)
\(-1,8\)
\(2, \frac{1}{3}\)
\(- \frac { 3 } { 4 } , 5\)
\(0,-4\)
\(0,7\)
\(\pm 7\)
\(\pm 2\)
\(- 3,1,3\)
\(- 5 , - 1,1\)

Contestar

1. \(x ^ { 2 } - 2 x - 15 = 0\)

3. \(3 x ^ { 2 } - 7 x + 2 = 0\)

5. \(x ^ { 2 } + 4 x = 0\)

7. \(x ^ { 2 } - 49 = 0\)

9. \(x ^ { 3 } - x ^ { 2 } - 9 x + 9 = 0\)

Ejercicio\(\PageIndex{9}\)

Encuentra una función con las raíces dadas.

\(\frac { 1 } { 2 } , \frac { 2 } { 3 }\)
\(\frac { 2 } { 5 } , - \frac { 1 } { 3 }\)
\(\pm \frac { 3 } { 4 }\)
\(\pm \frac { 5 } { 2 }\)
\(5\)doble raíz
\(-3\)doble raíz
\(-1,0,3\)
\(-5,0,2\)

Contestar

1. \(f ( x ) = 6 x ^ { 2 } - 7 x + 2\)

3. \(f ( x ) = 16 x ^ { 2 } - 9\)

5. \(f ( x ) = x ^ { 2 } - 10 x + 25\)

7. \(f ( x ) = x ^ { 3 } - 2 x ^ { 2 } - 3 x\)

Ejercicio\(\PageIndex{10}\)

Recordemos que si\(| X | = p\), entonces\(X=-p\) o\(X=p\). Utilice esto para resolver las siguientes ecuaciones de valor absoluto.

\(\left| x ^ { 2 } - 8 \right| = 8\)
\(\left| 2 x ^ { 2 } - 9 \right| = 9\)
\(\left| x ^ { 2 } - 2 x - 1 \right| = 2\)
\(\left| x ^ { 2 } - 8 x + 14 \right| = 2\)
\(\left| 2 x ^ { 2 } - 4 x - 7 \right| = 9\)
\(\left| x ^ { 2 } - 3 x - 9 \right| = 9\)

Contestar

1. \(\pm 4,0\)

3. \(\pm 1,3\)

5. \(- 2,1,4\)

Ejercicio\(\PageIndex{11}\)

Explicar a un estudiante principiante de álgebra la diferencia entre una ecuación y una expresión.
¿Cuál es la diferencia entre una raíz y una\(x\) -intercepción? Explique.
Crea una función con tres raíces reales de tu elección. Gráficalo con una utilidad gráfica y verifica tus resultados. Comparte tu función en el panel de discusión.
Investigar y discutir el teorema fundamental del álgebra.

Contestar

1. La respuesta puede variar

3. La respuesta puede variar

Notas al pie

²⁰ Un producto es igual a cero si y sólo si al menos uno de los factores es cero.

²¹ El proceso de resolver una ecuación que es igual a cero factorizándola y luego estableciendo cada factor variable igual a cero.

²² Un valor en el dominio de una función que da como resultado cero.

²³ Garantiza que habrá tantas (o menos) raíces a una función polinómica con una variable como su grado.

²⁴ Una raíz que se repite dos veces.