1.6: Visualizar fracciones
- Page ID
- 110444
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Encuentra fracciones equivalentes
- Simplificar fracciones
- Multiplicar fracciones
- Dividir fracciones
- Simplificar expresiones escritas con una barra de fracciones
- Traducir frases a expresiones con fracciones
Una introducción más completa a los temas tratados en esta sección se puede encontrar en el capítulo Preálgebra, Fracciones.
Buscar Fracciones Equivalentes
Las fracciones son una forma de representar partes de un todo. La fracción\(\dfrac{1}{3}\) significa que un todo se ha dividido en 3 partes iguales y cada parte es una de las tres partes iguales. Ver Figura\(\PageIndex{1}\). La fracción\(\dfrac{2}{3}\) representa dos de tres partes iguales. En la fracción\(\dfrac{2}{3}\), al 2 se le llama numerador y al 3 se le llama denominador.
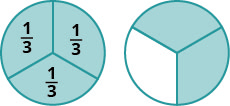
Se escribe una fracción\(\dfrac{a}{b}\), donde\(b\neq 0\) y
- \(a\)es el numerador y\(b\) es el denominador.
Una fracción representa partes de un todo. El denominador\(b\) es el número de partes iguales en las que se ha dividido el conjunto, y el numerador\(a\) indica cuántas partes están incluidas.
Si un pastel entero ha sido cortado en 6 pedazos y comemos los 6 pedazos, comimos\(\dfrac{6}{6}\) trozos, o, en otras palabras, un pastel entero.
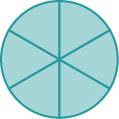
Entonces\(\dfrac{6}{6}=1\). Esto nos lleva a la propiedad de uno que nos dice que cualquier número, excepto cero, dividido por sí mismo lo es\(1\).
\[\dfrac{a}{a} = 1 \quad (a \neq 0)\]
Cualquier número, excepto cero, dividido por sí mismo es uno.
Hacer la actividad de Matemáticas Manipulativas “Fracciones Equivalentes a Uno” te ayudará a desarrollar una mejor comprensión de las fracciones que son equivalentes a una.
Si un pastel se cortaba en 6 pedazos y comíamos los 6, comíamos\(\dfrac{6}{6}\) trozos, o, en otras palabras, un pastel entero. Si el pastel se cortó en 8 pedazos y comimos los 8, comimos\(\dfrac{8}{8}\) trozos, o un pastel entero. Comimos la misma cantidad, un pastel entero.
Las fracciones\(\dfrac{6}{6}\) y\(\dfrac{8}{8}\) tienen el mismo valor, 1, y así se llaman fracciones equivalentes. Las fracciones equivalentes son fracciones que tienen el mismo valor.
Pensemos en pizzas esta vez. En la figura se\(\PageIndex{3}\) muestran dos imágenes: una sola pizza a la izquierda, cortada en dos trozos iguales, y una segunda pizza del mismo tamaño, cortada en ocho trozos a la derecha. Esta es una manera de demostrar que\(\dfrac{1}{2}\) es equivalente a\(\dfrac{4}{8}\). En otras palabras, son fracciones equivalentes.
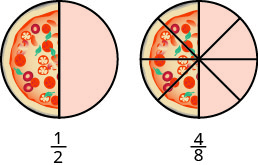
Las fracciones equivalentes son fracciones que tienen el mismo valor.
¿Cómo podemos usar las matemáticas para\(\dfrac{1}{2}\) cambiarnos\(\dfrac{4}{8}\)? ¿Cómo podríamos tomar una pizza que se corta en 2 trozos y cortarla en 8 trozos? ¡Podríamos cortar cada una de las 2 piezas más grandes en 4 piezas más pequeñas! Entonces, toda la pizza se cortaría en 88 piezas en lugar de solo 2. Matemáticamente, lo que hemos descrito podría escribirse así como\(\dfrac{1\cdot 4}{2\cdot 4} = \dfrac{4}{8}\). Ver Figura\(\PageIndex{4}\).
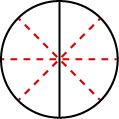
Este modelo conduce a la siguiente propiedad:
Si\(a,b,c\) son los números donde\(b\neq 0, c\neq 0\), entonces
\[\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\]
Si hubiéramos cortado la pizza de otra manera, podríamos conseguir
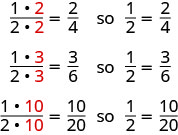
Entonces, decimos\(\dfrac{1}{2}\),,\(\dfrac{2}{4}\)\(\dfrac{3}{6}\), y\(\dfrac{10}{20}\) son fracciones equivalentes.
Hacer la actividad de Matemáticas Manipulativas “Fracciones Equivalentes” te ayudará a desarrollar una mejor comprensión de lo que significa cuando dos fracciones son equivalentes.
Encuentra tres fracciones equivalentes a\(\dfrac{2}{5}\).
- Contestar
-
Para encontrar una fracción equivalente a\(\dfrac{2}{5}\), multiplicamos el numerador y denominador por el mismo número. Podemos elegir cualquier número, excepto cero. Multipliquémoslos por 2, 3, y luego 5.
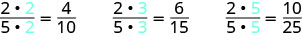
-
Entonces,\(\dfrac{4}{10}\),\(\dfrac{6}{15}\), y\(\dfrac{10}{25}\) son equivalentes a\(\dfrac{2}{5}\).
Encuentra tres fracciones equivalentes a\(\dfrac{3}{5}\).
- Contestar
-
\(\dfrac{6}{10}\),\(\dfrac{9}{15}\),\(\dfrac{12}{20}\); las respuestas pueden variar
Encuentra tres fracciones equivalentes a\(\dfrac{4}{5}\).
- Contestar
-
\(\dfrac{8}{10}\),\(\dfrac{12}{15}\),\(\dfrac{16}{20}\); las respuestas pueden variar
Simplificar fracciones
Una fracción se considera simplificada si no hay factores comunes, distintos de 1, en su numerador y denominador.
Por ejemplo,
- \(\dfrac{2}{3}\)se simplifica porque no hay factores comunes de 2 y 3.
- \(\dfrac{10}{15}\)no se simplifica porque 5 es un factor común de 10 y 15.
Una fracción se considera simplificada si no hay factores comunes en su numerador y denominador.
La frase reducir una fracción significa simplificar la fracción. Simplificamos o simplificamos una fracción eliminando los factores comunes del numerador y el denominador. Una fracción no se simplifica hasta que se hayan eliminado todos los factores comunes. Si una expresión tiene fracciones, no se simplifica completamente hasta que se simplifican las fracciones.
En Ejercicio\(\PageIndex{4}\), se utilizó la propiedad de fracciones equivalentes para encontrar fracciones equivalentes. Ahora usaremos la propiedad de fracciones equivalentes a la inversa para simplificar las fracciones. Podemos reescribir la propiedad para mostrar ambas formas juntas.
Si\(a,b,c\) son números donde\(b\neq 0,c\neq 0\),
\[\text{then } \dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c} \text{ and } \dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\]
Simplificar:\(-\dfrac{32}{56}\)
- Contestar
-
\(-\dfrac{32}{56}\) Reescribir el numerador y denominador mostrando los factores comunes. \(-\dfrac{4\cdot 8}{7\cdot 8}\) Simplifique el uso de la propiedad de fracciones equivalentes. \(-\dfrac{4}{7}\) Observe que la fracción\(-\dfrac{4}{7}\) se simplifica porque no hay más factores comunes.
Simplificar:\(-\dfrac{42}{54}\)
- Contestar
-
\(-\dfrac{7}{9}\)
Simplificar:\(-\dfrac{42}{54}\)
- Contestar
-
\(-\dfrac{5}{9}\)
A veces puede que no sea fácil encontrar factores comunes del numerador y denominador. Cuando esto sucede, una buena idea es facturar el numerador y el denominador en números primos s. luego dividir los factores comunes usando la propiedad de fracciones equivalentes.
Simplificar:\(-\dfrac{210}{385}\)
- Contestar
-



Simplificar:\(-\dfrac{69}{120}\)
- Contestar
-
\(-\dfrac{23}{40}\)
Simplificar:\(-\dfrac{120}{192}\)
- Contestar
-
\(-\dfrac{5}{8}\)
Ahora resumimos los pasos que debes seguir para simplificar fracciones.
- Reescribir el numerador y denominador para mostrar los factores comunes.
Si es necesario, factive primero el numerador y el denominador en números primos. - Simplifique el uso de la propiedad de fracciones equivalentes dividiendo los factores comunes.
- Multiplique los factores restantes, si es necesario.
Simplificar:\(\dfrac{5x}{5y}\)
- Contestar
-
\(\dfrac{5x}{5y}\) Reescriba mostrando los factores comunes, luego divida los factores comunes. 
Simplificar. \(\dfrac{x}{y}\)
Simplificar:\(\dfrac{7x}{7y}\)
- Contestar
-
\(\dfrac{x}{y}\)
Simplificar:\(\dfrac{3a}{3b}\)
- Contestar
-
\(\dfrac{a}{b}\)
Multiplicar fracciones
A muchas personas les resulta más fácil multiplicar y dividir fracciones que sumar y restar fracciones. Entonces comenzaremos con la multiplicación de fracciones.
Hacer la actividad de Matemáticas Manipulativas “Multiplicación de Fracciones Modelo” te ayudará a desarrollar una mejor comprensión de la multiplicación de fracciones.Usaremos un modelo para mostrarte cómo multiplicar dos fracciones y para ayudarte a recordar el procedimiento. Empecemos con\(\dfrac{3}{4}\).

Ahora vamos a tomar\(\dfrac{1}{2}\) de\(\dfrac{3}{4}\).

Observe que ahora, el conjunto se divide en 8 partes iguales. Entonces\(\dfrac{1}{2}\cdot \dfrac{3}{4}=\dfrac{3}{8}\).
Para multiplicar fracciones, multiplicamos los numeradores y multiplicamos los denominadores.
Si\(a,b,c\) y\(d\) son los números donde\(b\neq 0\) y\(d\neq 0\), entonces
\[\dfrac{a}{b}\cdot\dfrac{c}{d} = \dfrac{ac}{bd}\]
Para multiplicar fracciones, multiplicar los numeradores y multiplicar los denominadores.
Al multiplicar fracciones, las propiedades de los números positivos y negativos siguen aplicándose, por supuesto. Es una buena idea determinar el signo del producto como primer paso. En Ejercicio\(\PageIndex{13}\), vamos a multiplicar negativo y un positivo, por lo que el producto será negativo.
Multiplicar:\(-\dfrac{11}{12}\cdot \dfrac{5}{7}\)
- Contestar
-
El primer paso es encontrar el signo del producto. Dado que los signos son los diferentes, el producto es negativo.
\[\begin{array} {ll} {} & {-\dfrac{11}{12}\cdot \dfrac{5}{7}} \\{\text{Determine the sign of the product; multiply.}} &{-\dfrac{11\cdot 5}{12\cdot 7}} \\ {\text{Are there any common factors in the numerator}} &{} \\ {\text{and the denominator? No}} &{-\dfrac{55}{84}} \end{array}\]
Multiplicar:\(-\dfrac{10}{28}\cdot \dfrac{8}{15}\)
- Contestar
-
\(-\dfrac{4}{21}\)
Multiplicar:\(-\dfrac{9}{20}\cdot \dfrac{5}{12}\)
- Contestar
-
\(-\dfrac{3}{16}\)
Al multiplicar una fracción por un entero, puede ser útil escribir el entero como una fracción. Cualquier entero, a, puede escribirse como\(\dfrac{a}{1}\). Entonces, por ejemplo,\(3 = \dfrac{3}{1}\).
Multiplicar:\(-\dfrac{12}{5}(-20x)\)
- Contestar
-
Determinar el signo del producto. Los signos son los mismos, por lo que el producto es positivo.
\(-\dfrac{12}{5}(-20x)\) Escribir\(20x\) como una fracción. \(\dfrac{12}{5}(\dfrac{20x}{1})\) Multiplicar. Reescribe\(20\) para mostrar el factor común\(5\) y dividirlo. 
Simplificar. \(48x\)
Multiplicar:\(\dfrac{11}{3}(-9a)\)
- Contestar
-
\(-33a\)
Multiplicar:\(\dfrac{13}{7}(-14b)\)
- Contestar
-
\(-26b\)
Dividir fracciones
Ahora que sabemos multiplicar fracciones, estamos casi listos para dividirnos. Antes de que podamos hacer eso, que necesitamos algo de vocabulario.
El recíproco de una fracción se encuentra invirtiendo la fracción, colocando el numerador en el denominador y el denominador en el numerador. El recíproco de\(\dfrac{2}{3}\) es\(\dfrac{3}{2}\).
Fíjese en eso\(\dfrac{2}{3}\cdot\dfrac{3}{2} = 1\). Un número y su recíproco se multiplican a\(1\).
Para obtener un producto de positivo\(1\) al multiplicar dos números, los números deben tener el mismo signo. Por lo que los recíprocos deben tener el mismo signo.
El recíproco de\(-\dfrac{10}{7}\) es\(-\dfrac{7}{10}\), ya que\(-\dfrac{10}{7}(-\dfrac{7}{10}) = 1\).
El recíproco de\(\dfrac{a}{b}\) es\(\dfrac{b}{a}\).
Un número y su recíproco se multiplican a uno\(\dfrac{a}{b}\cdot\dfrac{b}{a} = 1\)
Hacer la actividad de Matemáticas Manipulativas “División de Fracciones Modelo” te ayudará a desarrollar una mejor comprensión de la división de fracciones.
Para dividir fracciones, multiplicamos la primera fracción por la recíproca de la segunda.
Si\(a,b,c\) y\(d\) son los números donde\(b\neq 0, c\neq 0\) y\(d\neq 0\), entonces
\[\dfrac{a}{b}\div\dfrac{c}{d} = \dfrac{a}{b}\cdot\dfrac{d}{c}\]
Para dividir fracciones, multiplicamos la primera fracción por la recíproca de la segunda.
¡Tenemos que decirlo\(b\neq 0, c\neq 0\) y\(d\neq 0\) estar seguros de que no dividimos por cero!
Dividir:\(-\dfrac{2}{3}\div\dfrac{n}{5}\)
- Contestar
-
\[\begin{array} {ll} {} & {-\dfrac{2}{3}\div \dfrac{n}{5}} \\{\text{To divide, multiply the first fraction by the}} &{-\dfrac{2}{3}\cdot\dfrac{5}{n}} \\ {\text{reciprocal of the second.}} &{} \\ {\text{Multiply.}} &{-\dfrac{10}{3n}} \end{array}\]
Dividir:\(-\dfrac{3}{5}\div\dfrac{p}{7}\).
- Contestar
-
\(-\dfrac{21}{5p}\)
Dividir:\(-\dfrac{5}{8}\div\dfrac{q}{3}\).
- Contestar
-
\(-\dfrac{15}{8q}\)
Encuentra el cociente:
\(-\dfrac{7}{18}\div (-\dfrac{14}{27})\)
- Contestar
-
\(-\dfrac{7}{18}\div(-\dfrac{14}{27})\) Para dividir, multiplicar la primera fracción por el recíproco de la segunda. \(-\dfrac{7}{18}\cdot -\dfrac{27}{14}\) Determinar el signo del producto, y luego multiplicar.. \(\dfrac{7\cdot 27}{18\cdot 14}\) Reescritura mostrando factores comunes. 
Eliminar factores comunes. \(\dfrac{3}{2\cdot 2}\) Simplificar. \(\dfrac{3}{4}\)
Encuentra el cociente:
\(-\dfrac{7}{8}\div (-\dfrac{14}{27})\)
- Contestar
-
\(\dfrac{4}{15}\)
Encuentra el cociente:
\(-\dfrac{7}{8}\div (-\dfrac{14}{27})\)
- Contestar
-
\(\dfrac{2}{3}\)
Hay varias maneras de recordar qué pasos tomar para multiplicar o dividir fracciones. Una forma es repetirte las llamadas a ti mismo. Si haces esto cada vez que haces un ejercicio, tendrás los pasos memorizados.
- “Para multiplicar fracciones, multiplicar los numeradores y multiplicar los denominadores”.
- “Para dividir fracciones, multiplicar la primera fracción por el recíproco de la segunda”.
Otra forma es tener en cuenta dos ejemplos:
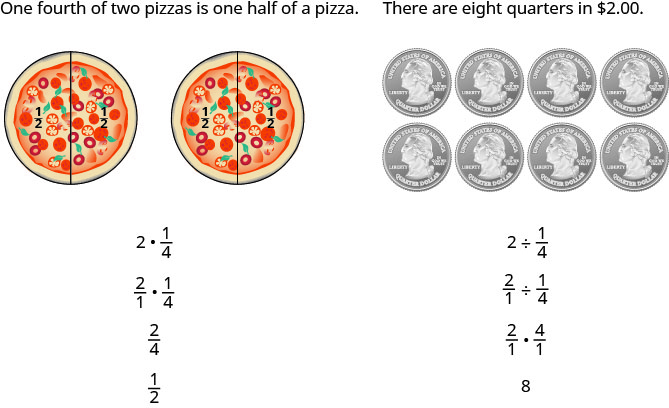
Los numeradores o denominadores de algunas fracciones contienen fracciones en sí mismas. Una fracción en la que el numerador o el denominador es una fracción se denomina fracción compleja.
Una fracción compleja es una fracción en la que el numerador o el denominador contiene una fracción.
Algunos ejemplos de fracciones complejas son:
\[\dfrac{\frac{6}{7}}{3} \quad \dfrac{\frac{3}{4}}{\frac{5}{8}} \quad \dfrac{\frac{x}{2}}{\frac{5}{6}}\]
Para simplificar una fracción compleja, recordamos que la barra de fracciones significa división. Por ejemplo, la fracción compleja\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) significa\(\dfrac{3}{4} \div \dfrac{5}{8}\).
Simplificar:\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\)
- Contestar
-
\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) Reescribir como división. \(\dfrac{3}{4} \div \dfrac{5}{8}\) Multiplicar la primera fracción por el recíproco de la segunda. \(\dfrac{3}{4} \cdot \dfrac{8}{5}\) Multiplicar. \(\dfrac{3\cdot 8}{4\cdot 5}\) Busque factores comunes. 
Divida los factores comunes y simplifique. \(\dfrac{6}{5}\)
Simplificar:\(\dfrac{\frac{2}{3}}{\frac{5}{6}}\)
- Contestar
-
\(\dfrac{4}{5}\)
Simplificar:\(\dfrac{\frac{3}{7}}{\frac{6}{11}}\)
- Contestar
-
\(\dfrac{11}{14}\)
Simplificar:\(\dfrac{\frac{x}{2}}{\frac{xy}{6}}\)
- Contestar
-
\(\dfrac{\frac{x}{2}}{\frac{xy}{6}}\) Reescribir como división. \(\dfrac{x}{2} \div \dfrac{xy}{6}\) Multiplicar la primera fracción por el recíproco de la segunda. \(\dfrac{x}{2} \cdot \dfrac{6}{xy}\) Multiplicar. \(\dfrac{x\cdot 6}{2\cdot xy}\) Busque factores comunes. 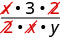
Divida los factores comunes y simplifique. \(\dfrac{3}{y}\)
Simplificar:\(\dfrac{\frac{a}{8}}{\frac{ab}{6}}\)
- Contestar
-
\(\dfrac{3}{4b}\)
Simplificar:\(\dfrac{\frac{p}{2}}{\frac{pq}{8}}\)
- Contestar
-
\(\dfrac{4}{q}\)
Simplifique expresiones con una barra de fracciones
La línea que separa el numerador del denominador en una fracción se denomina barra de fracción. Una barra de fracción actúa como símbolo de agrupación. El orden de las operaciones nos dice entonces que simplifiquemos el numerador y luego el denominador. Entonces dividimos.
Para simplificar la expresión\(\dfrac{5 - 3}{7 + 1}\), primero simplificamos el numerador y el denominador por separado. Entonces dividimos.
\[\begin{array} {l} {\dfrac{5 - 3}{7 + 1}} \\ {\dfrac{2}{8}} \\ {\dfrac{1}{4}} \end{array}\]
- Simplifica la expresión en el numerador. Simplifica la expresión en el denominador.
- Simplifica la fracción.
Simplificar:\(\dfrac{4 - 2(3)}{2^{2} + 2}\)
- Contestar
-
\[\begin{array} {ll} {} &{\dfrac{4 - 2(3)}{2^{2} + 2}} \\ {\text{Use the order of operations to simplify the}} &{\dfrac{4 - 6}{4 + 2}} \\ {\text{numerator and the denominator.}} &{} \\ {\text{Simplify the numerator and the denominator}} &{\dfrac{-2}{6}} \\ {\text{Simplify. A negative divided by a positive is negative.}} &{-\dfrac{1}{3}} \end{array}\]
Simplificar:\(\dfrac{6 - 3(5)}{3^{2} + 3}\)
- Contestar
-
\(-\dfrac{3}{4}\)
Simplificar:\(\dfrac{4 - 4(6)}{3^{2} + 3}\)
- Contestar
-
\(-\dfrac{5}{3}\)
¿A dónde va el signo negativo en una fracción? Por lo general, el signo negativo está frente a la fracción, pero a veces verá una fracción con un numerador negativo, o a veces con un denominador negativo. Recuerda que las fracciones representan división. Cuando el numerador y el denominador tienen signos diferentes, el cociente es negativo.
\[\begin{array} {ll} {\frac{-1}{3} = -\frac{1}{3}} &{\frac{\text{negative}}{\text{positive}} = \text{negative}} \\ {\frac{1}{-3} = -\frac{1}{3}} &{\frac{\text{positive}}{\text{negative}} = \text{negative}} \end{array}\]
Para cualquier número positivo\(a\) y\(b\),
\[\dfrac{-a}{b} = \dfrac{a}{-b} = -\dfrac{a}{b}\]
Simplificar:\(\frac{4(-3) + 6(-2)}{-3(2) - 2}\)
- Contestar
-
La barra de fracciones actúa como un símbolo de agrupación. Así que simplifica completamente el numerador y el denominador por separado.
\[\begin{array} {ll} {} &{\frac{4(-3) + 6(-2)}{-3(2) - 2}} \\{\text{Multiply.}} &{\frac{-12 + (-12)}{-6 - 2}} \\ {\text{Simplify.}} &{\frac{-24}{-8}} \\ {\text{Divide.}} &{3} \end{array}\]
Simplificar:\(\frac{8(-2) + 4(-3)}{-5(2) + 3}\)
- Contestar
-
\(4\)
Simplificar:\(\frac{7(-1) + 9(-3)}{-5(3) - 2}\)
- Contestar
-
\(2\)
Traducir frases a expresiones con fracciones
Ahora que hemos hecho algún trabajo con fracciones, estamos listos para traducir frases que resultarían en expresiones con fracciones.
Las palabras inglesas cociente y ratio se utilizan a menudo para describir fracciones. Recuerda que “cociente” significa división. El cociente de aa y bb es el resultado que obtenemos al dividir\(a\) por\(b\), o\(\dfrac{a}{b}\).
Traducir la frase en inglés en una expresión algebraica: el cociente de la diferencia de\( m\) y\(n\), y\(p\).
- Contestar
-
Estamos buscando el cociente de la diferencia de\(m\) y\(n\), y\(p\).. Esto significa que queremos dividir la diferencia de\(m\) y\(n\), y\(p\).
\[\dfrac{m - n}{p}\]
Traducir la frase en inglés en una expresión algebraica: el cociente de la diferencia de\(a\) y\(b\), y\(cd\).
- Contestar
-
\(\dfrac{a - b}{cd}\)
Traducir la frase en inglés en una expresión algebraica: el cociente de la suma de\(p\) y\(q\), y\(r\).
- Contestar
-
\(\dfrac{p + q}{r}\)
Conceptos clave
- Propiedad de fracciones equivalentes: Si\(a, b, c\) son números donde\(b\neq 0, c\neq 0\), entonces
\(\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\) y\(\dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\) - División de Fracción: Si\(a, b, c\) y\(d\) son números dónde\(b\neq 0, c\neq 0\) y\(d \neq 0\), entonces\(\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\). Para dividir fracciones, multiplique la primera fracción por el recíproco de la segunda.
- Multiplicación de Fracciones: Si\(a,b,c\) y\(d\) son números donde\(b\neq 0, d\neq 0\), entonces\(\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}\). Para multiplicar fracciones, multiplicar los numeradores y multiplicar los denominadores.
- Colocación de Signo Negativo en una Fracción: Para cualquier número positivo\(a\) y\(b\),\(\dfrac{-a}{a} = \dfrac{a}{-a} = -\dfrac{a}{b}\)
- Propiedad de Uno:\(\dfrac{a}{a} = 1\); Cualquier número, excepto cero, dividido por sí mismo es uno.
- Simplificar una fracción
- Reescribir el numerador y denominador para mostrar los factores comunes. Si es necesario, factifique primero el numerador y el denominador en números primos.
- Simplifique el uso de la propiedad de fracciones equivalentes dividiendo los factores comunes.
- Multiplique cualquier factor restante.
- Simplifique una expresión con una barra de fracciones
- Simplifica la expresión en el numerador. Simplifica la expresión en el denominador.
- Simplifica la fracción.
Glosario
- fracción compleja
- Una fracción compleja es una fracción en la que el numerador o el denominador contiene una fracción.
- denominador
- El denominador es el valor en la parte inferior de la fracción que indica el número de partes iguales en las que se ha dividido el todo.
- fracciones equivalentes
- Las fracciones equivalentes son fracciones que tienen el mismo valor.
- fracción
- Se escribe una fracción\(\frac{a}{b}\), donde\(b\neq 0\), a es el numerador y b es el denominador. Una fracción representa partes de un todo. El denominador b es el número de partes iguales en las que se ha dividido el conjunto, y el numerador aa indica cuántas partes están incluidas.
- numerador
- El numerador es el valor en la parte superior de la fracción que indica cuántas partes del conjunto están incluidas.
- recíproco
- El recíproco de\(\frac{a}{b}\) es\(\frac{b}{a}\). Un número y su recíproco se multiplican a uno:\(\frac{a}{b}\cdot \frac{b}{a} = 1\).
- fracción simplificada
- Una fracción se considera simplificada si no hay factores comunes en su numerador y denominador.


