4.2E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 110270

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La práctica hace la perfección

Reconocer la relación entre las soluciones de una ecuación y su gráfica

En los siguientes ejercicios, por cada par ordenado, decide:

¿El par ordenado es una solución a la ecuación?
¿Está el punto en la línea?

Ejercicio$\PageIndex{1}$

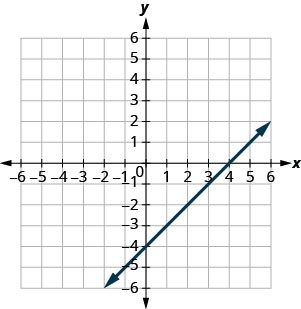
y=x+2

(0,2)
(1,2)
(−1,1)
(−3, −1)

$La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va del negativo 7 al 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 6, negativo 4), (negativo 5, negativo 3), (negativo 4, negativo 2), (negativo 3, negativo 1), (negativo 2, 0), (negativo 1, 1), (0, 2), (1, 3), (2, 4), (3, 5), (4, 6), y (5, 7).$

Contestar

sí; no
no; no
si; si
si; si

Ejercicio$\PageIndex{2}$

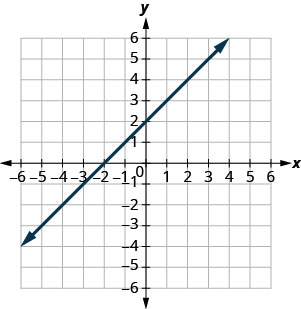
y=x−4

(0, −4)
(3, −1)
(2,2)
(1, −5)

$La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va del negativo 7 al 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 3, negativo 7), (negativo 2, negativo 6), (negativo 1, negativo 5), (0, negativo 4), (1, negativo 3), (2, negativo 2), (3, negativo 1), (4, 0), (5, 1), (6, 2), y (7, 3).$

Ejercicio$\PageIndex{3}$

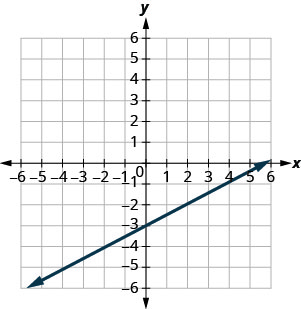
$y=\frac{1}{2} x-3$

(0, −3)
(2, −2)
(−2, −4)
(4,1)

$La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va del negativo 7 al 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 6, negativo 6), (negativo 4, negativo 5), (negativo 2, negativo 4), (0, negativo 3), (2, negativo 2), (4, negativo 1), y (6, 0).$

Contestar

si; si
si; si
si; si
no; no

Ejercicio$\PageIndex{4}$

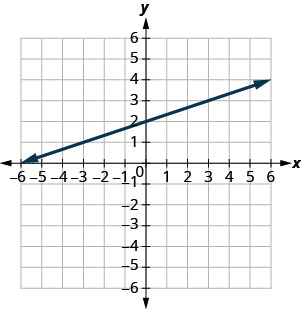
$y=\frac{1}{3} x+2$

(0,2)
(3,3)
(−3,2)
(−6,0)

Graficar una ecuación lineal trazando puntos

En los siguientes ejercicios, grafica por puntos de trazado.

Ejercicio$\PageIndex{5}$

$y=3 x-1$

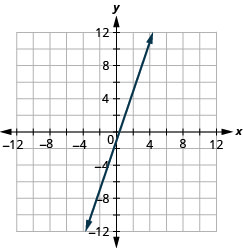
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La recta pasa por los puntos (negativo 3, negativo 10), (negativo 2, negativo 7), (negativo 1, negativo 4), (0, negativo 1), (1, 2), (2, 5) y (3, 8).$

Ejercicio$\PageIndex{6}$

$y=2 x+3$

Ejercicio$\PageIndex{7}$

$y=-2 x+2$

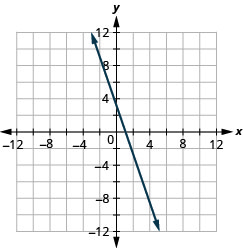
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La recta pasa por los puntos (negativo 4, 10), (negativo 3, 8), (negativo 2, 6), (negativo 1, 4), (0, 2), (1, 0), (2, negativo 2), (3, negativo 4), (4, negativo 6), y (5, negativo 8).$

Ejercicio$\PageIndex{8}$

$y=-3 x+1$

Ejercicio$\PageIndex{9}$

$y=x+2$

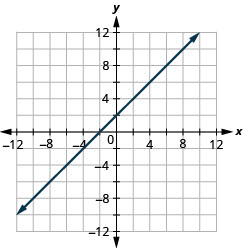
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La recta pasa por los puntos (negativo 10, negativo 8), (negativo 9, negativo 7), (negativo 8, negativo 6), (negativo 7, negativo 5), (negativo 6, negativo 4), (negativo 5, negativo 3), (negativo 4, negativo 2), (negativo 3, negativo 1), (negativo 2, 0), (negativo 1, 1), (0, 2), (1, 1 3), (2, 4), (3, 5 ), (4, 6), (5, 7), (6, 8), (7, 9) y (8, 10).$

Ejercicio$\PageIndex{10}$

$y=x-3$

Ejercicio$\PageIndex{11}$

$y=-x-3$

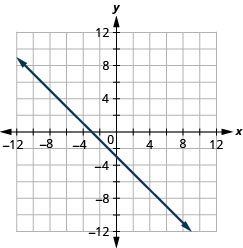
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La recta pasa por los puntos (negativo 10, 7), (negativo 9, 6), (negativo 8, 5), (negativo 7, 4), (negativo 6, 3), (negativo 5, 2), (negativo 4, 1), (negativo 3, 0), (negativo 2, negativo 1), (negativo 1, negativo 2), (0, negativo 3), (1, negativo 4), (2, negativo 5), (3, negativo 6), (4, negativo 7) , (5, negativo 8), (6, negativo 9) y (7, negativo 10).$

Ejercicio$\PageIndex{12}$

$y=-x-2$

Ejercicio$\PageIndex{13}$

$y=2 x$

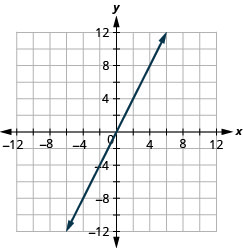
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La recta pasa por los puntos (negativo 5, negativo 10), (negativo 4, negativo 8), (negativo 3, negativo 6), (negativo 2, negativo 4), (negativo 1, negativo 2), (0, 0), (1, 2), (2, 4), (3, 6), (4, 8), y (5, 10).$

Ejercicio$\PageIndex{14}$

$y=3 x$

Ejercicio$\PageIndex{15}$

$y=-4 x$

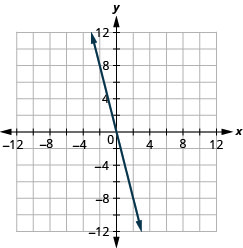
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La recta pasa por los puntos (negativo 3, 12), (negativo 2, 8), (negativo 1, 4), (0, 0), (1, negativo 4), (2, negativo 8), y (3, negativo 12).$

Ejercicio$\PageIndex{16}$

$y=-2 x$

Ejercicio$\PageIndex{17}$

$y=\frac{1}{2} x+2$

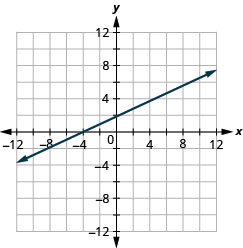
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La recta pasa por los puntos (negativo 12, negativo 4), (negativo 10, negativo 3), (negativo 8, negativo 2), (negativo 6, negativo 1), (negativo 4, 0), (negativo 2, 1), (0, 2), (2, 3), (4, 4), (6, 5), (8, 6), y (10, 7).$

Ejercicio$\PageIndex{18}$

$y=\frac{1}{3} x-1$

Ejercicio$\PageIndex{19}$

$y=\frac{4}{3} x-5$

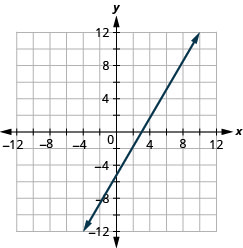
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La recta pasa por los puntos (negativo 3, negativo 9), (0, negativo 5), (3, negativo 1), (6, 3) y (9, 7).$

Ejercicio$\PageIndex{20}$

$y=\frac{3}{2} x-3$

Ejercicio$\PageIndex{21}$

$y=-\frac{2}{5} x+1$

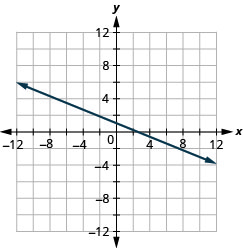
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La recta pasa por los puntos (negativo 10, 5), (negativo 5, 3), (0, 1), (5, negativo 1), y (10, negativo 3).$

Ejercicio$\PageIndex{22}$

$y=-\frac{4}{5} x-1$

Ejercicio$\PageIndex{23}$

$y=-\frac{3}{2} x+2$

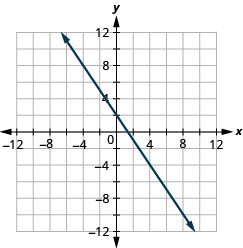
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La recta pasa por los puntos (negativo 6, 11), (negativo 4, 8), (negativo 2, 5), (0, 2), (2, negativo 1), (4, negativo 4), (6, negativo 7), y (8, negativo 10).$

Ejercicio$\PageIndex{24}$

$y=-\frac{5}{3} x+4$

Ejercicio$\PageIndex{25}$

$x+y=6$

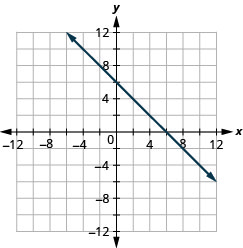
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La recta pasa por los puntos (negativo 4, 10), (negativo 3, 9), (negativo 2, 8), (negativo 1, 7), (0, 6), (1, 5), (2, 4), (3, 3), (4, 2), (5, 1), (6, 0), (7, negativo 1), (8, negativo 2), (9, negativo 3), y (10, negativo 4).$

Ejercicio$\PageIndex{26}$

$x+y=4$

Ejercicio$\PageIndex{27}$

$x+y=-3$

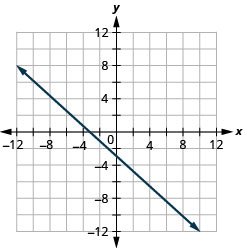
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La recta pasa por los puntos (negativo 10, 7), (negativo 9, 6), (negativo 8, 5), (negativo 7, 4), (negativo 6, 3), (negativo 5, 2), (negativo 4, 1), (negativo 3, 0), (negativo 2, negativo 1), (negativo 1, negativo 2), (0, negativo 3), (1, negativo 4), (2, negativo 5), (3, negativo 6), (4, negativo 7) , (5, negativo 8), (6, negativo 9) y (7, negativo 10).$

Ejercicio$\PageIndex{28}$

$x+y=-2$

Ejercicio$\PageIndex{29}$

$x-y=2$

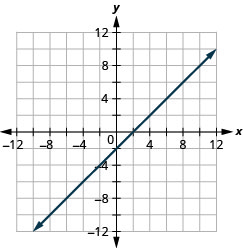
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La recta pasa por los puntos (negativo 8, negativo 10), (negativo 7, negativo 9), (negativo 6, negativo 8), (negativo 5, negativo 7), (negativo 4, negativo 6), (negativo 3, negativo 5), (negativo 2, negativo 4), (negativo 1, negativo 3), (0, negativo 2), (1, negativo 1), (2, 0), (3, 1), (4, 2), (5, 3 ), (6, 4), (7, 5), (8, 6), (9, 7) y (10, 8).$

Ejercicio$\PageIndex{30}$

$x-y=1$

Ejercicio$\PageIndex{31}$

$x-y=-1$

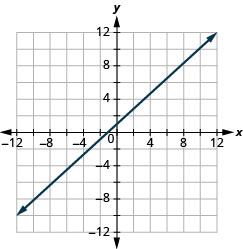
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La recta pasa por los puntos (negativo 9, negativo 8), (negativo 8, negativo 7), (negativo 7, negativo 6), (negativo 6, negativo 5), (negativo 5, negativo 4), (negativo 4, negativo 3), (negativo 3, negativo 2), (negativo 2, negativo 1), (negativo 1, 0), (0, 1), (1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7), (7, 8), (8, 9) y (9, 10).$

Ejercicio$\PageIndex{32}$

$x-y=-3$

Ejercicio$\PageIndex{33}$

$3 x+y=7$

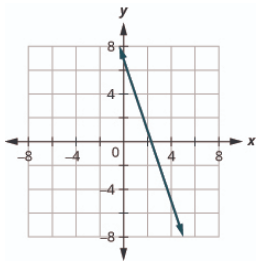
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 7 a -7. Se grafica la ecuación 3 x más y es igual a 7.$

Ejercicio$\PageIndex{34}$

$5x+y=6$

Ejercicio$\PageIndex{35}$

2x+y=−3

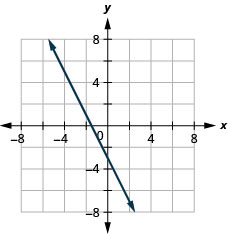
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va del negativo 7 al 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 5, 7), (negativo 4, 5), (negativo 3, 3), (negativo 2, 1), (negativo 1, negativo 1), (0, negativo 3), (1, negativo 5), y (2, negativo 7).$

Ejercicio$\PageIndex{36}$

$4x+y=−5$

Ejercicio$\PageIndex{37}$

$\frac{1}{3} x+y=2$

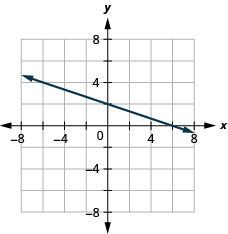
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va del negativo 7 al 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 6, 4), (negativo 3, 3), (0, 2), (3, 1) y (6, 0).$

Ejercicio$\PageIndex{38}$

$\frac{1}{2} x+y=3$

Ejercicio$\PageIndex{39}$

$\frac{2}{5} x-y=4$

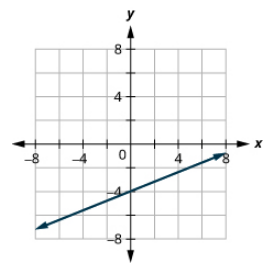
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va del negativo 7 al 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 5, negativo 2), (0, negativo 4) y (5, negativo 6).$

Ejercicio$\PageIndex{40}$

$\frac{3}{4} x-y=6$

Ejercicio$\PageIndex{41}$

$2 x+3 y=12$

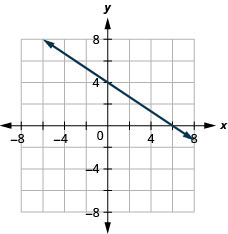
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va del negativo 7 al 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 3, 6), (0, 4), (3, 2) y (6, 0).$

Ejercicio$\PageIndex{42}$

4x+2y=12

Ejercicio$\PageIndex{43}$

3x−4y=12

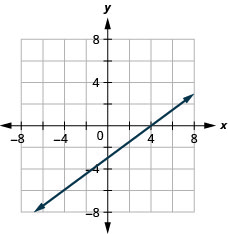
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va del negativo 7 al 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 4, negativo 6), (0, negativo 3), (4, 0) y (8, 3).$

Ejercicio$\PageIndex{44}$

2x−5y=10

Ejercicio$\PageIndex{45}$

x−6y=3

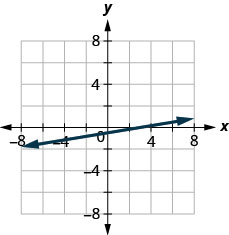
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va del negativo 7 al 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 6, negativo tres mitades), (negativo 3, negativo 1), (0, negativo una mitad), (3, 0) y (6, una mitad).$

Ejercicio$\PageIndex{46}$

x−4y=2

Ejercicio$\PageIndex{47}$

5x+2y=4

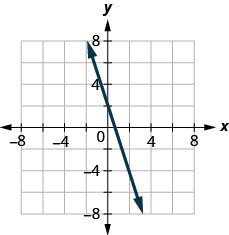
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va del negativo 7 al 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 2, 7), (0, 2), (2, negativo 3), y (4, negativo 8).$

Ejercicio$\PageIndex{48}$

3x+5y=5

Gráfica líneas verticales y horizontales

En los siguientes ejercicios, grafica cada ecuación.

Ejercicio$\PageIndex{49}$

x=4

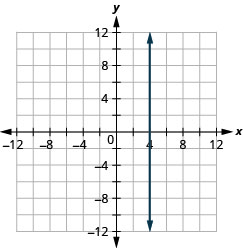
Contestar: $La figura muestra una línea vertical recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La línea vertical pasa por los puntos (4, 0), (4, 1), (4, 2) y todos los puntos con la primera coordenada 4.$

Ejercicio$\PageIndex{50}$

x=3

Ejercicio$\PageIndex{51}$

x=−2

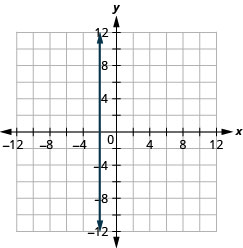
Contestar: $La figura muestra una línea vertical recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La línea vertical pasa por los puntos (negativo 2, 0), (negativo 2, 1), (negativo 2, 2) y todos los puntos con primera coordenada negativa 2.$

Ejercicio$\PageIndex{52}$

x=−5

Ejercicio$\PageIndex{53}$

y=3

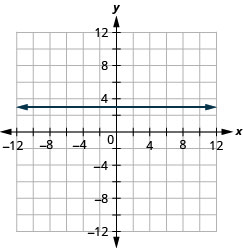
Contestar: $La figura muestra una línea horizontal recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La línea horizontal pasa por los puntos (0, 3), (1, 3), (2, 3) y todos los puntos con segunda coordenada 3.$

Ejercicio$\PageIndex{54}$

y=1

Ejercicio$\PageIndex{55}$

y=−5

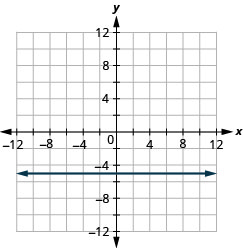
Contestar: $La figura muestra una línea horizontal recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La línea horizontal pasa por los puntos (0, negativo 5), (1, negativo 5), (2, negativo 5) y todos los puntos con segunda coordenada negativa 5.$

Ejercicio$\PageIndex{56}$

y=−2

Ejercicio$\PageIndex{57}$

$x=\frac{7}{3}$

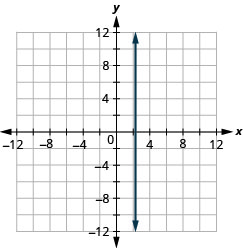
Contestar: $La figura muestra una línea vertical recta dibujada en el plano de la coordenada x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. La línea vertical pasa por los puntos (7/3, 0), (7/3, 1), (7/3, 2) y todos los puntos con la primera coordenada 7/3.$

Ejercicio$\PageIndex{58}$

$x=\frac{5}{4}$

Ejercicio$\PageIndex{59}$

$y=-\frac{15}{4}$

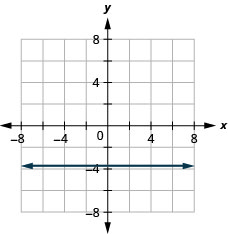
Contestar: $La figura muestra una línea horizontal recta dibujada en el plano de la coordenada x y. El eje x del plano va del negativo 7 al 7. El eje y del plano va de negativo 7 a 7. La línea horizontal pasa por los puntos (0, negativo 15/4), (1, negativo 15/4), (2, negativo 15/4) y todos los puntos con segunda coordenada negativa 15/4.$

Ejercicio$\PageIndex{60}$

$y=-\frac{5}{3}$

En los siguientes ejercicios, grafica cada par de ecuaciones en un mismo sistema de coordenadas rectangulares.

Ejercicio$\PageIndex{61}$

y=2x e y=2

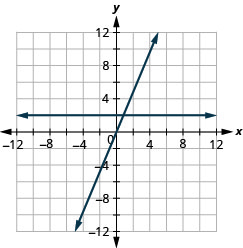
Contestar: $La figura muestra dos líneas rectas dibujadas en el mismo plano de coordenadas x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. Una línea es una recta horizontal que atraviesa los puntos (negativo 4, 2) (0, 2), (4, 2), y todos los demás puntos con la segunda coordenada 2. La otra línea es una línea inclinada que atraviesa los puntos (negativo 5, negativo 10), (negativo 4, negativo 8), (negativo 3, negativo 6), (negativo 2, negativo 4), (negativo 1, negativo 2), (0, 0), (1, 2), (2, 4), (3, 6), (4, 8) y (5, 10).$

Ejercicio$\PageIndex{62}$

y=5x e y=5

Ejercicio$\PageIndex{63}$

$y=-\frac{1}{2} x$y$y=-\frac{1}{2}$

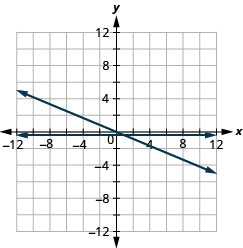
Contestar: $La figura muestra dos líneas rectas dibujadas en el mismo plano de coordenadas x y. El eje x del plano va de negativo 12 a 12. El eje y del plano va de negativo 12 a 12. Una línea es una recta horizontal que atraviesa los puntos (negativo 4, negativo una mitad) (0, mitad negativa), (4, mitad negativa), y todos los demás puntos con segunda coordenada negativa una mitad. La otra línea es una línea inclinada que atraviesa los puntos (negativo 10, 5), (negativo 8, 4), (negativo 6, 3), (negativo 4, 2), (negativo 2, 1), (0, 0), (1, negativo 2), (2, negativo 4), (3, negativo 6), (4, negativo 8) y (5, negativo 10).$

Ejercicio$\PageIndex{64}$

$y=-\frac{1}{3} x$y$y=-\frac{1}{3}$

Práctica Mixta

En los siguientes ejercicios, grafica cada ecuación.

Ejercicio$\PageIndex{65}$

y=4x

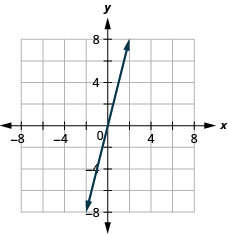
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va del negativo 7 al 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 2, negativo 8), (negativo 1, negativo 4), (0, 0), (1, 4) y (2, 8).$

Ejercicio$\PageIndex{66}$

y=2x

Ejercicio$\PageIndex{67}$

$y=-\frac{1}{2} x+3$

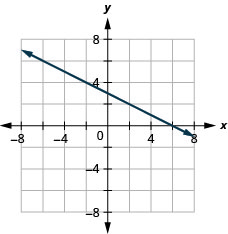
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va del negativo 7 al 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 6, 6), (negativo 4, 5), (negativo 2, 4), (0, 3), (2, 2), (4, 1) y (6, 0).$

Ejercicio$\PageIndex{68}$

$y=\frac{1}{4} x-2$

Ejercicio$\PageIndex{69}$

y=−x

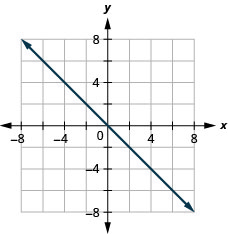
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de 7 negativo a 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 6, 6), (negativo 5, 5), (negativo 4, 4), (negativo 3, 3), (negativo 2, 2), (negativo 1, 1), (0, 0), (1, negativo 1), (2, negativo 2), (3, negativo 3), (4, negativo 4), (5, negativo 5), y (6, negativo 3), (6, negativo 4), (5, negativo 5), y (6, negativo 3), negativo 6).$

Ejercicio$\PageIndex{70}$

y=x

Ejercicio$\PageIndex{71}$

x−y=3

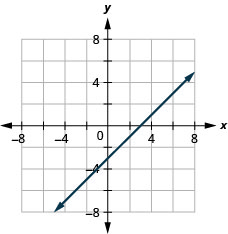
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de 7 negativo a 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 3, negativo 7), (negativo 2, negativo 6), (negativo 1, negativo 4), (0, negativo 3), (1, negativo 2), (2, negativo 1), (3, 0), (4, 1), (5, 2) y (6, 3).$

Ejercicio$\PageIndex{72}$

x+y=−5

Ejercicio$\PageIndex{73}$

4x+y=2

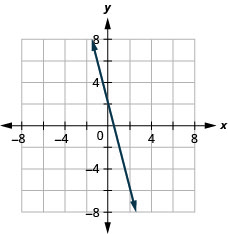
Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de 7 negativo a 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 2, 6), (negativo 1, 4), (0, 2), (1, negativo 2), y (2, negativo 6).$

Ejercicio$\PageIndex{74}$

2x+y=6

Ejercicio$\PageIndex{75}$

y=−1

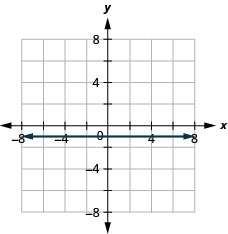
Contestar: $La figura muestra una línea horizontal recta dibujada en el plano de la coordenada x y. El eje x del plano va de 7 negativo a 7. El eje y del plano va de negativo 7 a 7. La línea horizontal pasa por los puntos (0, negativo 1), (1, negativo 1), (2, negativo 1) y todos los puntos con segunda coordenada negativa 1.$

Ejercicio$\PageIndex{76}$

y=5

Ejercicio$\PageIndex{77}$

2x+6y=12

Contestar: $La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de 7 negativo a 7. El eje y del plano va de negativo 7 a 7. La recta pasa por los puntos (negativo 6, 4), (negativo 3, 3), (0, 2), (3, 1) y (6, 0).$

Ejercicio$\PageIndex{78}$

5x+2y=10

Ejercicio$\PageIndex{79}$

x=3

Contestar: $La figura muestra una línea vertical recta dibujada en el plano de la coordenada x y. El eje x del plano va de 7 negativo a 7. El eje y del plano va de negativo 7 a 7. La línea vertical pasa por los puntos (3, 0), (3, 1), (3, 2) y todos los puntos con la primera coordenada 3.$

Ejercicio$\PageIndex{80}$

x=−4

Matemáticas cotidianas

Ejercicio$\PageIndex{81}$

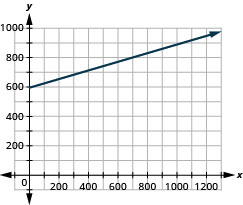
Costo de la casa rodante. Los Robinsons alquilaron una casa rodante por una semana para irse de vacaciones. Les costó $594 más $0.32 por milla para rentar la casa rodante, por lo que la ecuación lineal y=594+0.32x da el costo, yy, por conducir xx millas. Calcule el costo de alquiler para conducir 400, 800 y 1200 millas, y luego graficar la línea.

Contestar

$722, $850, $978

$La figura muestra una línea recta dibujada en el plano de la coordenada x y. El eje x del plano va de 0 a 1200 en incrementos de 100. El eje y del plano va de 0 a 1000 en incrementos de 100. La recta inicia en el punto (0, 594) y pasa por los puntos (400, 722), (800, 850), y (1200, 978). El extremo derecho de la línea tiene una flecha apuntando hacia arriba y hacia la derecha.$

Ejercicio$\PageIndex{82}$

Ganancias semanales. En la galería de arte donde trabaja, a Salvador se le pagan $200 semanales más el 15% de las ventas que realiza, por lo que la ecuación y=200+0.15x da la cantidad, yy, gana por vender x dólares de obra de arte. Calcula la cantidad que Salvador gana por vender $900, $1600 y $2000, y luego grafica la línea.

Ejercicios de escritura

Ejercicio$\PageIndex{83}$

Explica cómo elegirías tres$x$ - valores para hacer una tabla para graficar la línea$y=\frac{1}{5} x-2$

Responder: Las respuestas variarán.

Ejercicio$\PageIndex{84}$

¿Cuál es la diferencia entre las ecuaciones de una línea vertical y una horizontal?

Autocomprobación

ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.

$Esta tabla tiene 4 filas y 4 columnas. La primera fila es una fila de encabezado y etiqueta cada columna. El encabezado de la primera columna es “Puedo...”, el segundo es “Con confianza”, el tercero es “Con algo de ayuda”, y el cuarto es “No, no lo pillo”. Debajo de la primera columna se encuentran las frases “... reconocer la relación entre las soluciones de una ecuación y su gráfica”, “... graficar una ecuación lineal trazando puntos.”, y “... graficar líneas verticales y horizontales”. Las otras columnas se dejan en blanco para que el alumno pueda indicar su nivel de dominio para cada tema.$

ⓑ Después de revisar esta lista de verificación, ¿qué harás para tener confianza para todos los objetivos?

La práctica hace la perfección

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejercicio\(\PageIndex{15}\)

Ejercicio\(\PageIndex{16}\)

Ejercicio\(\PageIndex{17}\)

Ejercicio\(\PageIndex{18}\)

Ejercicio\(\PageIndex{19}\)

Ejercicio\(\PageIndex{20}\)

Ejercicio\(\PageIndex{21}\)

Ejercicio\(\PageIndex{22}\)

Ejercicio\(\PageIndex{23}\)

Ejercicio\(\PageIndex{24}\)

Ejercicio\(\PageIndex{25}\)

Ejercicio\(\PageIndex{26}\)

Ejercicio\(\PageIndex{27}\)

Ejercicio\(\PageIndex{28}\)

Ejercicio\(\PageIndex{29}\)

Ejercicio\(\PageIndex{30}\)

Ejercicio\(\PageIndex{31}\)

Ejercicio\(\PageIndex{32}\)

Ejercicio\(\PageIndex{33}\)

Ejercicio\(\PageIndex{34}\)

Ejercicio\(\PageIndex{35}\)

Ejercicio\(\PageIndex{36}\)

Ejercicio\(\PageIndex{37}\)

Ejercicio\(\PageIndex{38}\)

Ejercicio\(\PageIndex{39}\)

Ejercicio\(\PageIndex{40}\)

Ejercicio\(\PageIndex{41}\)

Ejercicio\(\PageIndex{42}\)

Ejercicio\(\PageIndex{43}\)

Ejercicio\(\PageIndex{44}\)

Ejercicio\(\PageIndex{45}\)

Ejercicio\(\PageIndex{46}\)

Ejercicio\(\PageIndex{47}\)

Ejercicio\(\PageIndex{48}\)

Ejercicio\(\PageIndex{49}\)

Ejercicio\(\PageIndex{50}\)

Ejercicio\(\PageIndex{51}\)

Ejercicio\(\PageIndex{52}\)

Ejercicio\(\PageIndex{53}\)

Ejercicio\(\PageIndex{54}\)

Ejercicio\(\PageIndex{55}\)

Ejercicio\(\PageIndex{56}\)

Ejercicio\(\PageIndex{57}\)

Ejercicio\(\PageIndex{58}\)

Ejercicio\(\PageIndex{59}\)

Ejercicio\(\PageIndex{60}\)

Ejercicio\(\PageIndex{61}\)

Ejercicio\(\PageIndex{62}\)

Ejercicio\(\PageIndex{63}\)

Ejercicio\(\PageIndex{64}\)

Práctica Mixta

Ejercicio\(\PageIndex{65}\)

Ejercicio\(\PageIndex{66}\)

Ejercicio\(\PageIndex{67}\)

Ejercicio\(\PageIndex{68}\)

Ejercicio\(\PageIndex{69}\)

Ejercicio\(\PageIndex{70}\)

Ejercicio\(\PageIndex{71}\)

Ejercicio\(\PageIndex{72}\)

Ejercicio\(\PageIndex{73}\)

Ejercicio\(\PageIndex{74}\)

Ejercicio\(\PageIndex{75}\)

Ejercicio\(\PageIndex{76}\)

Ejercicio\(\PageIndex{77}\)

Ejercicio\(\PageIndex{78}\)