6.3: Multiplicar polinomios
- Page ID
- 110375
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Multiplicar un polinomio por un monomio
- Multiplicar un binomio por un binomio
- Multiplicar un trinomio por un binomio
Antes de comenzar, toma este cuestionario de preparación.
- Distribuir:\(2(x+3)\).
Si te perdiste este problema, revisa Ejercicio 1.10.31. - Combina términos similares:\(x^{2}+9x+7x+63\).
Si te perdiste este problema, revisa Ejercicio 1.3.37.
Multiplicar un polinomio por un monomio
Hemos utilizado la Propiedad Distributiva para simplificar expresiones como\(2(x−3)\). Multiplicaste ambos términos entre paréntesis,\(x\) y\(3\), por\(2\), para obtener\(2x−6\). Con el nuevo vocabulario de este capítulo, se puede decir que estaba multiplicando un binomio\(x−3\),, por un monomio,\(2\).
¡Multiplicar un binomio por un monomio no es nada nuevo para ti! Aquí hay un ejemplo:
Multiplicar:\(4(x+3)\).
- Contestar
-
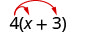
Distribuir. \(4 \cdot x+4 \cdot 3\) Simplificar. \(4 x+12\)
Multiplicar:\(5(x+7)\).
- Contestar
-
5x+35
Multiplicar:\(3(y+13)\).
- Contestar
-
3y+39
Multiplicar: y (y−2).
- Contestar
-
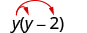
Distribuir. \(y \cdot y-y \cdot 2\) Simplificar. \(y^{2}-2 y\)
Multiplicar:\(x(x−7)\).
- Contestar
-
\(x^{2}-7 x\)
Multiplicar:\(d(d−11)\).
- Contestar
-
\(d^{2}-11d\)
Multiplicar:\(7x(2 x+y)\)
- Contestar
-
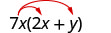
Distribuir. 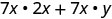
Simplificar. 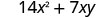
Multiplicar:\(5x(x+4 y)\)
- Contestar
-
\(5 x^{2}+20 x y\)
Multiplicar:\(2p(6 p+r)\)
- Contestar
-
\(12 p^{2}+2 p r\)
Multiplicar:\(-2 y\left(4 y^{2}+3 y-5\right)\)
- Contestar
-

Distribuir. 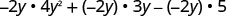
Simplificar. 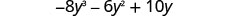
Multiplicar:\(-3 y\left(5 y^{2}+8 y-7\right)\)
- Contestar
-
\(-15 y^{3}-24 y^{2}+21 y\)
Multiplicar:\(4x^{2}\left(2 x^{2}-3 x+5\right)\)
- Contestar
-
\(8 x^{4}-24 x^{3}+20 x^{2}\)
Multiplicar:\(2x^{3}\left(x^{2}-8 x+1\right)\)
- Contestar
-

Distribuir. \(2 x^{3} \cdot x^{2}+\left(2 x^{3}\right) \cdot(-8 x)+\left(2 x^{3}\right) \cdot 1\) Simplificar. \(2 x^{5}-16 x^{4}+2 x^{3}\)
Multiplicar: 4\(x\left(3 x^{2}-5 x+3\right)\)
- Contestar
-
\(12 x^{3}-20 x^{2}+12 x\)
Multiplicar:\(-6 a^{3}\left(3 a^{2}-2 a+6\right)\)
- Contestar
-
\(-18 a^{5}+12 a^{4}-36 a^{3}\)
Multiplicar:\((x+3) p\)
- Contestar
-
El monomio es el segundo factor. 
Distribuir. \(x \cdot p+3 \cdot p\) Simplificar. \ (\ x p+3 p)
Multiplicar:\((x+8) p\)
- Contestar
-
\(x p+8 p\)
Multiplicar:\((a+4) p\)
- Contestar
-
\(a p+4 p\)
Multiplicar un Binomio por un Binomio
Al igual que hay diferentes formas de representar la multiplicación de números, existen varios métodos que se pueden utilizar para multiplicar un binomio por un binomio. Comenzaremos por usar la Propiedad Distributiva.
Multiplicar un Binomio por un Binomial Usando la Propiedad Distributiva
Mira Ejercicio\(\PageIndex{16}\), donde multiplicamos un binomio por un monomio.
| Instrucciones | Expresión |
|---|---|
| Expresiones de inicio |  |
| Distribuimos el\(p\) para obtener: | 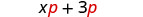 |
| ¿Y si tenemos\((x + 7)\) en lugar de\(p\)? |  |
| Distribuir\((x + 7)\). | 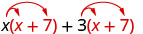 |
| Distribuir de nuevo. | \(x^{2}+7 x+3 x+21\) |
| Combina términos similares. | \(x^{2}+10 x+21\) |
Observe que antes de combinar términos similares, tenía cuatro términos. Multiplicaste los dos términos del primer binomio por los dos términos del segundo binomio, cuatro multiplicaciones.
Multiplicar:\((y+5)(y+8)\)
- Contestar
-

Distribuir (y + 8). 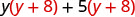
Distribuir de nuevo \(y^{2}+8 y+5 y+40\) Combina términos similares. \ (\ y^ {2} +13 y+40)
Multiplicar:\((x+8)(x+9)\)
- Contestar
-
\(x^{2}+17 x+72\)
Multiplicar:\((5 x+9)(4 x+3)\)
- Contestar
-
\(20 x^{2}+51 x+27\)
Multiplicar:\((2 y+5)(3 y+4)\)
- Contestar
-

Distribuir (3 y + 4). 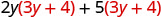
Distribuir de nuevo \(6 y^{2}+8 y+15 y+20\) Combina términos similares. \(6 y^{2}+23 y+20\)
Multiplicar:\((3 b+5)(4 b+6)\)
- Contestar
-
\(12 b^{2}+38 b+30\)
Multiplicar:\((a+10)(a+7)\)
- Contestar
-
\(a^{2}+17 a+70\)
Multiplicar:\((4 y+3)(2 y-5)\)
- Contestar
-

Distribuir. 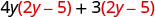
Distribuir de nuevo. \(8 y^{2}-20 y+6 y-15\) Combina términos similares. \(8 y^{2}-14 y-15\)
Multiplicar:\((5 y+2)(6 y-3)\)
- Contestar
-
\(30 y^{2}-3 y-6\)
Multiplicar:\((3 c+4)(5 c-2)\)
- Contestar
-
\(15 c^{2}+14 c-8\)
Multiplicar:\((x-2)(x-y)\)
- Contestar
-

Distribuir. 
Distribuir de nuevo. \(x^{2}-x y-2 x+2 y\) No hay términos similares para combinar.
Multiplicar:\((a+7)(a-b)\)
- Contestar
-
\(a^{2}-a b+7 a-7 b\)
Multiplicar:\((x+5)(x-y)\)
- Contestar
-
\(x^{2}-x y+5 x-5 y\)
Multiplicar un Binomio por un Binomial Usando el Método FOIL
Recuerda que cuando multiplicas un binomio por un binomio obtienes cuatro términos. A veces puedes combinar términos similares para obtener un trinomio, pero a veces, como en Ejercicio\(\PageIndex{28}\), no hay términos similares para combinar.
Veamos de nuevo el último ejemplo y prestemos especial atención a cómo conseguimos los cuatro términos.
\[\begin{array}{c}{(x-2)(x-y)} \\ {x^{2}-x y-2 x+2 y}\end{array} \nonumber\]
¿De dónde vino el primer término\(x^{2}\),,?

Abreviamos “Primero, Exterior, Interior, Último” como FOIL. Las letras significan 'F irst, O uter, I nner, L ast'. La palabra FOIL es fácil de recordar y asegura que encontremos los cuatro productos.
\[\begin{array}{c}{(x-2)(x-y)} \\ {x^{2}-x y-2 x+2 y} \\ {F \qquad O\qquad I\qquad L}\end{array}\]
Veamos (x+3) (x+7).
| Propiedad distributiva | PAPEL DE ALUMINIO |
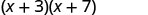 |
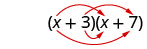 |
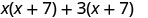 |
|
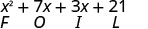 |
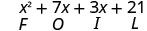 |
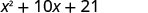 |
\(x^{2}+10 x+21\) |
Observe cómo los términos de la tercera línea se ajustan al patrón FOIL.
Ahora haremos un ejemplo donde usamos el patrón FOIL para multiplicar dos binomios.
Multiplicar usando el método FOIL:\((x+5)(x+9)\)
- Contestar
-

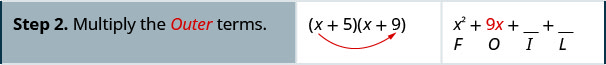
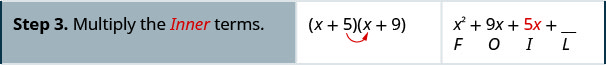
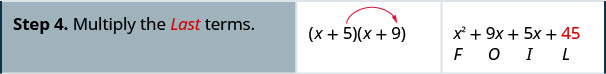

Multiplicar usando el método FOIL:\((x+6)(x+8)\)
- Contestar
-
\(x^{2}+14 x+48\)
Multiplicar usando el método FOIL:\((y+17)(y+3)\)
- Contestar
-
\(y^{2}+20 y+51\)
A continuación resumimos los pasos del método FOIL. El método FOIL solo se aplica a multiplicar binomios, ¡no a otros polinomios!

Cuando multiplicas por el método FOIL, dibujar las líneas ayudará a que tu cerebro se concentre en el patrón y facilitará su aplicación.
Multiplicar:\((y−7)(y+4)\).
- Contestar
-

Multiplicar:\((x−7)(x+5)\).
- Contestar
-
\(x^{2}-2 x-35\)
Multiplicar: (b−3) (b+6).
- Contestar
-
\(b^{2}+3 b-18\)
Multiplicar:\((4x+3)(2x−5)\).
- Contestar
-

Multiplicar:\((3x+7)(5x−2)\).
- Contestar
-
\(15 x^{2}+29 x-14\)
Multiplicar:\((4y+5)(4y−10)\).
- Contestar
-
\(16 y^{2}-20 y-50\)
Los productos finales en los últimos cuatro ejemplos fueron trinomios porque podíamos combinar los dos términos medios. No siempre es así.
Multiplicar:\((3x−y)(2x−5)\).
- Contestar
-
\((3 x-y)(2 x-5)\) 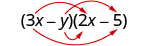
Multiplicar el Primero. 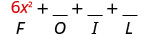
Multiplicar el Exterior. 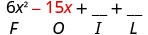
Multiplicar el Interior. 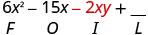
Multiplicar el Último. 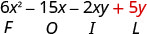
Combina términos similares, no hay ninguno. \(6 x^{2}-15 x-2 x y+5 y\)
Multiplicar: (10c−d) (c−6).
- Contestar
-
\(10 c^{2}-60 c-c d+6 d\)
Multiplicar: (7x−y) (2x−5).
- Contestar
-
\(14 x^{2}-35 x-2 x y+10 y\)
Ten cuidado con los exponentes en el siguiente ejemplo.
Multiplicar:\(\left(n^{2}+4\right)(n-1)\)
- Contestar
-
\(\left(n^{2}+4\right)(n-1)\) 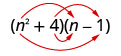
Multiplicar el Primero. 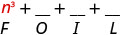
Multiplicar el Exterior. 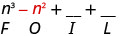
Multiplicar el Interior. 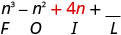
Multiplicar el Último. 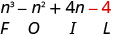
Combina términos similares, no hay ninguno. \ (\ n^ {3} -n^ {2} +4 n-4)
Multiplicar:\(\left(x^{2}+6\right)(x-8)\)
- Contestar
-
\(x^{3}-8 x^{2}+6 x-48\)
Multiplicar:\(\left(y^{2}+7\right)(y-9)\)
- Contestar
-
\(y^{3}-9 y^{2}+7 y-63\)
Multiplicar:\((3 p q+5)(6 p q-11)\)
- Contestar
-
\((3 p q+5)(6 p q-11)\) Multiplicar el Primero. 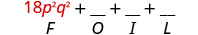

Multiplicar el Exterior. 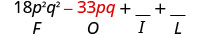
Multiplicar el Interior. 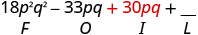
Multiplicar el Último. 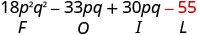
Combina términos similares, no hay ninguno. \(18 p^{2} q^{2}-3 p q-55\)
Multiplicar:\((2 a b+5)(4 a b-4)\)
- Contestar
-
\(8 a^{2} b^{2}+12 a b-20\)
Multiplicar:\((2 x y+3)(4 x y-5)\)
- Contestar
-
\(8 x^{2} y^{2}+2 x y-15\)
Multiplicar un binomio por un binomio usando el método vertical
El método FOIL suele ser el método más rápido para multiplicar dos binomios, pero solo funciona para binomios. Puede utilizar la Propiedad Distributiva para encontrar el producto de cualquiera de dos polinomios. Otro método que funciona para todos los polinomios es el Método Vertical. Es muy parecido al método que usas para multiplicar números enteros. Observe con atención este ejemplo de multiplicar números de dos dígitos.

Ahora aplicaremos este mismo método para multiplicar dos binomios.
Multiplicar usando el Método Vertical:\((3 y-1)(2 y-6)\)
- Contestar
-
No importa qué binomio vaya en la parte superior.
\[\begin{array}{lll}{\text { Multiply } 3 y-1 \text { by }-6 \text { . }}&& \\ {\text { Multiply } 3 y-1 \text { by } 2 y \text { . }}& &\\ \\ &{\qquad\space3 y-1} & \\& {\dfrac{ \space\space\times 2 y-6}{\quad-18 y+6}} & \text{partial product} & \\ &
(click for details)& \text{partial product} & \\ \text{Add like terms.} &&\text{product} \end{array}\]Callstack: at (Bookshelves/Matematicas/Algebra/Libro:_Algebra_elemental_(OpenStax)/06:_Polinomios/6.03:_Multiplicar_polinomios), /content/body/div[4]/div[3]/div[1]/div/dl/dd/p[2]/span/span, line 1, column 3Observe que los productos parciales son los mismos que los términos en el método FOIL.
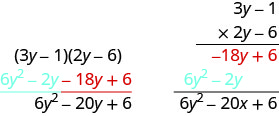
Multiplicar usando el Método Vertical:\((5 m-7)(3 m-6)\)
- Contestar
-
\(15 m^{2}-51 m+42\)
Multiplicar usando el Método Vertical:\((6 b-5)(7 b-3)\)
- Contestar
-
\(42 b^{2}-53 b+15\)
Ahora hemos utilizado tres métodos para multiplicar binomios. Asegúrate de practicar cada método, y trata de decidir cuál prefieres. Los métodos se enumeran aquí todos juntos, para ayudarte a recordarlos.
Para multiplicar binomios, use:
- Propiedad distributiva
- Método FOIL
- Método Vertical
Recuerda, FOIL solo funciona al multiplicar dos binomios.
Multiplicar un Trinomio por un Binomio
Hemos multiplicado los monomios por monomios, los monomios por los polinomios y los binomios por los binomios. Ahora estamos listos para multiplicar un trinomio por un binomio. Recuerde, FOIL no funcionará en este caso, pero podemos usar ya sea la Propiedad Distributiva o el Método Vertical. Primero miramos un ejemplo usando la Propiedad Distributiva.
Multiplicar usando la Propiedad Distributiva:\((b+3)\left(2 b^{2}-5 b+8\right)\)
- Contestar
-
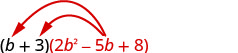
Distribuir. 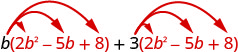
Multiplicar. \(2 b^{3}-5 b^{2}+8 b+6 b^{2}-15 b+24\) Combina términos similares. \(2 b^{3}+b^{2}-7 b+24\)
Multiplicar usando la Propiedad Distributiva:\((y-3)\left(y^{2}-5 y+2\right)\)
- Contestar
-
\(y^{3}-8 y^{2}+17 y-6\)
Multiplicar usando la Propiedad Distributiva:\((x+4)\left(2 x^{2}-3 x+5\right)\)
- Contestar
-
\(2 x^{3}+5 x^{2}-7 x+20\)
Ahora hagamos esta misma multiplicación usando el Método Vertical.
Multiplicar usando el Método Vertical:\((b+3)\left(2 b^{2}-5 b+8\right)\)
- Contestar
-
Es más fácil poner el polinomio con menos términos en la parte inferior porque obtenemos menos productos parciales de esta manera.
Multiplicar\((2b^2 − 5b + 8)\) por 3. 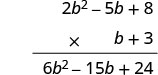
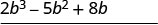
Multiplicar\((2b^2 − 5b + 8)\) por\(b\). \(2 b^{3}+b^{2}-7 b+24\) Agregar términos similares.
Multiplicar usando el Método Vertical:\((y-3)\left(y^{2}-5 y+2\right)\)
- Contestar
-
\(y^{3}-8 y^{2}+17 y-6\)
Multiplicar usando el Método Vertical:\((x+4)\left(2 x^{2}-3 x+5\right)\)
- Contestar
-
\(2 x^{3}+5 x^{2}-7 x+20\)
Ahora hemos visto dos métodos que puedes usar para multiplicar un trinomio por un binomio. Después de practicar cada método, probablemente encontrarás que prefieres una forma sobre la otra. Enumeramos ambos métodos que se enumeran aquí, para una fácil referencia.
Para multiplicar un trinomio por un binomio, use el:
- Propiedad distributiva
- Método Vertical
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con polinomios multiplicadores:
- Multiplicar exponentes 1
- Multiplicar exponentes 2
- Multiplicar exponentes 3
Conceptos clave
- Método FOIL para multiplicar dos binomios —Para multiplicar dos binomios:
- Multiplicar los primeros términos.
- Multiplicar los términos externos.
- Multiplicar los términos internos.
- Multiplicar los últimos términos.
- Multiplicar dos binomios —Para multiplicar binomios, utilice el:
- Multiplicar un Trinomio por un Binomio —Para multiplicar un trinomio por un binomio, use el:


